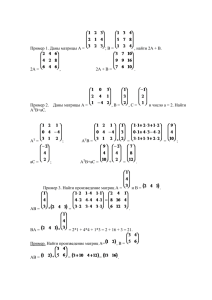
Матричная алгебра

Федеральное агентство по образованию
Уральский государственный экономический университет
Ю. Б. Мельников
Матричная алгебра
Раздел электронного учебника
для сопровождения практического занятия
Изд. 3-е, испр. и доп.
e-mail:
melnikov@k66.ru,
melnikov@r66.ru
сайты:
http://melnikov.k66.ru,
http://melnikov.web.ur.ru
Екатеринбург
2010
Пример 1 умножения матрицы на число
6
Пример 2 (формула произведения матриц)
24
Пример 3 (умножение на макроуровне)
33
Пример 4 (умножение на макроуровне)
50
Пример 5 (умножение на макроуровне)
63
Пример 6 к доказательству критерия обратимости матрицы 89
Пример 7 (обратная к матрице 2 × 2)
102
Пример 8 нахождения обратной матрицы
106
Упражнения на усвоение формулы умножения матриц140
Задача I.1
141
Задача I.2
142
Задача I.3
143
Произведение матриц
143
Задача II.4
144
Многочлен от матрицы
144
Задача III.5
145
Умножение «на макроуровне» (т.е. «по строчкам и
столбцам»)
145
Задача IV.6
146
Задача IV.7
147
Задача IV.8
148
Задача IV.9
149
Обратная матрица
149
Задача V.10
150
Задача V.11
151
Задача V.12
152
Задача V.13
153
Матричные уравнения
153
Задача VI.14
154
Задача VI.15
155
Задача VI.16
156
Ответы и решения
157
Пример 1. Вычислить 100 ·
Решение.
3 −2 −1 4
−3 0 2 1
Пример 1. Вычислить 100 ·
Решение.
100 ·
3 −2 −1 4
−3 0 2 1
3 −2 −1 4
−3 0 2 1
=
Пример 1. Вычислить 100 ·
Решение.
100 ·
3 −2 −1 4
−3 0 2 1
3 −2 −1 4
−3 0 2 1
=
300
.
Пример 1. Вычислить 100 ·
Решение.
100 ·
3 −2 −1 4
−3 0 2 1
3 −2 −1 4
−3 0 2 1
=
300
.
Пример 1. Вычислить 100 ·
Решение.
100 ·
3 −2 −1 4
−3 0 2 1
3 −2 −1 4
−3 0 2 1
=
300 −200
.
Пример 1. Вычислить 100 ·
Решение.
100 ·
3 −2 −1 4
−3 0 2 1
3 −2 −1 4
−3 0 2 1
=
300 −200
.
Пример 1. Вычислить 100 ·
Решение.
100 ·
3 −2 −1 4
−3 0 2 1
3 −2 −1 4
−3 0 2 1
=
300 −200 −100
.
Пример 1. Вычислить 100 ·
Решение.
100 ·
3 −2 −1 4
−3 0 2 1
3 −2 −1 4
−3 0 2 1
=
300 −200 −100
.
Пример 1. Вычислить 100 ·
Решение.
100 ·
3 −2 −1 4
−3 0 2 1
3 −2 −1 4
−3 0 2 1
=
300 −200 −100 400
.
Пример 1. Вычислить 100 ·
Решение.
100 ·
3 −2 −1 4
−3 0 2 1
3 −2 −1 4
−3 0 2 1
=
300 −200 −100 400
.
Пример 1. Вычислить 100 ·
Решение.
100 ·
3 −2 −1 4
−3 0 2 1
3 −2 −1 4
−3 0 2 1
=
300 −200 −100 400
−300
.
Пример 1. Вычислить 100 ·
Решение.
100 ·
3 −2 −1 4
−3 0 2 1
3 −2 −1 4
−3 0 2 1
=
300 −200 −100 400
−300
.
Пример 1. Вычислить 100 ·
Решение.
100 ·
3 −2 −1 4
−3 0 2 1
3 −2 −1 4
−3 0 2 1
=
300 −200 −100 400
−300
0
.
Пример 1. Вычислить 100 ·
Решение.
100 ·
3 −2 −1 4
−3 0 2 1
3 −2 −1 4
−3 0 2 1
=
300 −200 −100 400
−300
0
.
Пример 1. Вычислить 100 ·
Решение.
100 ·
3 −2 −1 4
−3 0 2 1
3 −2 −1 4
−3 0 2 1
=
300 −200 −100 400
−300
0 200
.
Пример 1. Вычислить 100 ·
Решение.
100 ·
3 −2 −1 4
−3 0 2 1
3 −2 −1 4
−3 0 2 1
=
300 −200 −100 400
−300
0 200
.
Пример 1. Вычислить 100 ·
Решение.
100 ·
3 −2 −1 4
−3 0 2 1
3 −2 −1 4
−3 0 2 1
=
300 −200 −100 400
−300
0 200 100
.
Пример 1. Вычислить 100 ·
Решение.
100 ·
3 −2 −1 4
−3 0 2 1
Вернуться к лекции?
3 −2 −1 4
−3 0 2 1
=
300 −200 −100 400
−300
0 200 100
.
Пример 2. Даны матрицы P = (pij )s×t и Q = (qij )t×r . Запишите с помощью знака суммирования Σ и «в рассыпанном виде» формулу для вычисления коэффициентов матрицы R = P · Q.
Решение.
Пример 2. Даны матрицы P = (pij )s×t и Q = (qij )t×r . Запишите с помощью знака суммирования Σ и «в рассыпанном виде» формулу для вычисления коэффициентов матрицы R = P · Q.
Решение.
rmn =
t
X
i=1
Пример 2. Даны матрицы P = (pij )s×t и Q = (qij )t×r . Запишите с помощью знака суммирования Σ и «в рассыпанном виде» формулу для вычисления коэффициентов матрицы R = P · Q.
Решение.
rmn =
t
X
i=1
p q
Пример 2. Даны матрицы P = (pij )s×t и Q = (qij )t×r . Запишите с помощью знака суммирования Σ и «в рассыпанном виде» формулу для вычисления коэффициентов матрицы R = P · Q.
Решение.
rmn =
t
X
i=1
pm q n
Пример 2. Даны матрицы P = (pij )s×t и Q = (qij )t×r . Запишите с помощью знака суммирования Σ и «в рассыпанном виде» формулу для вычисления коэффициентов матрицы R = P · Q.
Решение.
rmn =
t
X
i=1
pmiqin
Пример 2. Даны матрицы P = (pij )s×t и Q = (qij )t×r . Запишите с помощью знака суммирования Σ и «в рассыпанном виде» формулу для вычисления коэффициентов матрицы R = P · Q.
Решение.
rmn =
t
X
i=1
pmiqin =
Пример 2. Даны матрицы P = (pij )s×t и Q = (qij )t×r . Запишите с помощью знака суммирования Σ и «в рассыпанном виде» формулу для вычисления коэффициентов матрицы R = P · Q.
Решение.
rmn =
t
X
i=1
pmiqin = pm1q1n +
Пример 2. Даны матрицы P = (pij )s×t и Q = (qij )t×r . Запишите с помощью знака суммирования Σ и «в рассыпанном виде» формулу для вычисления коэффициентов матрицы R = P · Q.
Решение.
rmn =
t
X
i=1
pmiqin = pm1q1n + pm2q2n +
Пример 2. Даны матрицы P = (pij )s×t и Q = (qij )t×r . Запишите с помощью знака суммирования Σ и «в рассыпанном виде» формулу для вычисления коэффициентов матрицы R = P · Q.
Решение.
rmn =
t
X
pmiqin = pm1q1n + pm2q2n + . . . + pmtqtn.
i=1
Вернуться к лекции?
Пример 3.С помощью
умножения матриц переставить в мат
1 2
рице A =  3 4  первую и последнюю строки.
5 6
Решение.
Пример 3.С помощью
умножения матриц переставить в мат
1 2
рице A =  3 4  первую и последнюю строки.
5 6


5 6
Решение. Должна получиться матрица B =  3 4 .
1 2
Пример 3.С помощью
умножения матриц переставить в мат
1 2
рице A =  3 4  первую и последнюю строки.
5 6


5 6
Решение. Первая строка получившейся матрицы B =  3 4 .
1 2
представляется в виде линейной комбинации строк матрицы A:
5 6 =0· 1 2 +0· 3 4 +1· 5 6 .
Пример 3.С помощью
умножения матриц переставить в мат
1 2
рице A =  3 4  первую и последнюю строки.
5 6


5 6
Решение. Первая строка получившейся матрицы B =  3 4 .
1 2
представляется в виде линейной комбинации строк матрицы A:
5 6 =0· 1 2 +0· 3 4 +1· 5 6 .
Поэтому первую строку матрицы B можно представить в виде произведения матриц следующим образом:


1
2
5 6 = 0 0 1  3 4 .
5 6
Пример 3.С помощью
умножения матриц переставить в мат
1 2
рице A =  3 4  первую и последнюю строки.
5 6


5 6
Решение. Первая строка получившейся матрицы B =  3 4 .
1 2
представляется в виде линейной комбинации строк матрицы A:
5 6 =0· 1 2 +0· 3 4 +1· 5 6 .
Поэтому первую строку матрицы B можно представить в виде произведения матриц следующим образом:


1
2
5 6 = 0 0 1 3 4
5 6
Пример 3.С помощью
умножения матриц переставить в мат
1 2
рице A =  3 4  первую и последнюю строки.
5 6


5 6
Решение. Первая строка получившейся матрицы B =  3 4 .
1 2
представляется в виде линейной комбинации строк матрицы A:
5 6 =0· 1 2 +0· 3 4 +1· 5 6 .
Поэтому первую строку матрицы B можно представить в виде произведения матриц следующим образом:


1
2
5 6 = 0 0 1 3 4
5 6
Пример 3.С помощью
умножения матриц переставить в мат
1 2
рице A =  3 4  первую и последнюю строки.
5 6


5 6
Решение. Первая строка получившейся матрицы B =  3 4 .
1 2
представляется в виде линейной комбинации строк матрицы A:
5 6 =0· 1 2 +0· 3 4 +1· 5 6 .
Поэтому первую строку матрицы B можно представить в виде произведения матриц следующим образом:


1
2
5 6 = 0 0 1 3 4
5 6
Пример 3.С помощью
умножения матриц переставить в мат
1 2
рице A =  3 4  первую и последнюю строки.
5 6


5 6
Решение. Вторая строка получившейся матрицы B =  3 4 .
1 2
представляется в виде линейной комбинации строк матрицы A:
3 4 =0· 1 2 +1· 3 4 +0· 5 6 .
Поэтому вторую строку матрицы B можно
изведения матриц следующим образом:

1
3 4 = 0 1 0 3
5
представить в виде про
2
4 .
6
Пример 3.С помощью
умножения матриц переставить в мат
1 2
рице A =  3 4  первую и последнюю строки.
5 6


5 6
Решение. Вторая строка получившейся матрицы B =  3 4 .
1 2
представляется в виде линейной комбинации строк матрицы A:
3 4 =0· 1 2 +1· 3 4 +0· 5 6 .
Поэтому вторую строку матрицы B можно представить в виде произведения матриц следующим образом:


1
2
3 4 = 0 1 0 3 4
5 6
Пример 3.С помощью
умножения матриц переставить в мат
1 2
рице A =  3 4  первую и последнюю строки.
5 6


5 6
Решение. Вторая строка получившейся матрицы B =  3 4 .
1 2
представляется в виде линейной комбинации строк матрицы A:
3 4 =0· 1 2 +1· 3 4 +0· 5 6 .
Поэтому вторую строку матрицы B можно представить в виде произведения матриц следующим образом:


1
2
3 4 = 0 1 0 3 4
5 6
Пример 3.С помощью
умножения матриц переставить в мат
1 2
рице A =  3 4  первую и последнюю строки.
5 6
Решение. Для третьей строки получаем аналогичный результат:
Пример 3.С помощью
умножения матриц переставить в мат
1 2
рице A =  3 4  первую и последнюю строки.
5 6
Решение. Для третьей строки получаем аналогичный результат:


1 2
1 2 = 1 0 0  3 4 ,
5 6
поскольку
Пример 3.С помощью
умножения матриц переставить в мат
1 2
рице A =  3 4  первую и последнюю строки.
5 6
Решение. Для третьей строки получаем аналогичный результат:


1 2
1 2 = 1 0 0  3 4 ,
5 6
поскольку
1 2 =1· 1 2 +0· 3 4 +0· 5 6 .
Пример 3.С помощью
умножения матриц переставить в мат
1 2
рице A =  3 4  первую и последнюю строки.
5 6
Решение. Получаем:

 


5 6
0 0 1
1 2
3 4=
 3 4 ,
1 2
5 6
Пример 3.С помощью
умножения матриц переставить в мат
1 2
рице A =  3 4  первую и последнюю строки.
5 6
Решение. Получаем:

 


5 6
0 0 1
1 2
 3 4  =  0 1 0  3 4 ,
1 2
5 6
Пример 3.С помощью
умножения матриц переставить в мат
1 2
рице A =  3 4  первую и последнюю строки.
5 6
Решение. Получаем:

 


5 6
0 0 1
1 2
 3 4  =  0 1 0  3 4 ,
1 2
1 0 0
5 6
Пример 3.С помощью
умножения матриц переставить в мат
1 2
рице A =  3 4  первую и последнюю строки.
5 6
Решение. Получаем:

 


5 6
0 0 1
1 2
 3 4  =  0 1 0  3 4 .
1 2
1 0 0
5 6
Вернуться к лекции «умножение на макроуровне»?
Пример 4. Подобрать хотя бы одно решение уравнения




0 1 0
1 0 0
 0 0 1 X =  0 1 0 
1 0 0
0 0 1
Решение.
Пример 4. Подобрать хотя бы одно решение уравнения




0 1 0
1 0 0
 0 0 1 X =  0 1 0 
1 0 0
0 0 1
Решение.


0 1 0
?
 0 0 1  ?
1 0 0
?



1 0 0
=0 1 0
0 0 1
Пример 4. Подобрать хотя бы одно решение уравнения




0 1 0
1 0 0
 0 0 1 X =  0 1 0 
1 0 0
0 0 1
Решение.


0 1 0
?
 0 0 1  ?
1 0 0
?



1 0 0
=0 1 0
0 0 1
Пример 4. Подобрать хотя бы одно решение уравнения




0 1 0
1 0 0
 0 0 1 X =  0 1 0 
1 0 0
0 0 1
Решение.


0 1 0
?
 0 0 1  ?
1 0 0
?



1 0 0
=0 1 0
0 0 1
Пример 4. Подобрать хотя бы одно решение уравнения




0 1 0
1 0 0
 0 0 1 X =  0 1 0 
1 0 0
0 0 1
Решение.


0 1 0
?
 0 0 1  1
1 0 0
?



1 0 0
=0 1 0
0 0 1
Пример 4. Подобрать хотя бы одно решение уравнения




0 1 0
1 0 0
 0 0 1 X =  0 1 0 
1 0 0
0 0 1
Решение.


0 1 0
0
 0 0 1  1
1 0 0
0



1 0 0
=0 1 0
0 0 1
Пример 4. Подобрать хотя бы одно решение уравнения




0 1 0
1 0 0
 0 0 1 X =  0 1 0 
1 0 0
0 0 1
Решение.


0 1 0
0 ?
 0 0 1  1 ?
1 0 0
0 ?



1 0 0
=0 1 0
0 0 1
Пример 4. Подобрать хотя бы одно решение уравнения




0 1 0
1 0 0
 0 0 1 X =  0 1 0 
1 0 0
0 0 1
Решение.


0 1 0
0 ?
 0 0 1  1 ?
1 0 0
0 ?



1 0 0
=0 1 0
0 0 1
Пример 4. Подобрать хотя бы одно решение уравнения




0 1 0
1 0 0
 0 0 1 X =  0 1 0 
1 0 0
0 0 1
Решение.


0 1 0
0 0
 0 0 1  1 0
1 0 0
0 1



1 0 0
=0 1 0
0 0 1
Пример 4. Подобрать хотя бы одно решение уравнения




0 1 0
1 0 0
 0 0 1 X =  0 1 0 
1 0 0
0 0 1
Решение.


 

0 1 0
0 0 ?
1 0 0
 0 0 1  1 0 ?  =  0 1 0 
1 0 0
0 1 ?
0 0 1
Пример 4. Подобрать хотя бы одно решение уравнения




0 1 0
1 0 0
 0 0 1 X =  0 1 0 
1 0 0
0 0 1
Решение.


 

0 1 0
0 0 ?
1 0 0
 0 0 1  1 0 ?  =  0 1 0 
1 0 0
0 1 ?
0 0 1
Пример 4. Подобрать хотя бы одно решение уравнения




0 1 0
1 0 0
 0 0 1 X =  0 1 0 
1 0 0
0 0 1
Решение.


 

0 1 0
0 0 1
1 0 0
 0 0 1  1 0 0  =  0 1 0 
1 0 0
0 1 0
0 0 1
Пример 4. Подобрать хотя бы одно решение уравнения




0 1 0
1 0 0
 0 0 1 X =  0 1 0 
1 0 0
0 0 1
Решение.


 

0 1 0
0 0 1
1 0 0
 0 0 1  1 0 0  =  0 1 0 
1 0 0
0 1 0
0 0 1
Вернуться к лекции «умножение на макроуровне»?
Пример 5. Вычислить двумя способами матрицы

 

 

1
7 0 9 1
1 2 3
1 1

 
2 4 8 1 0
 4 5 6  ·  −1 1 

·
1 1 2 0 1
7 8 9
0 1
0
0 1 2 −1
Решение. Сколько вариантов можно предложить?

0

1
.
0
0
Пример 5. Вычислить двумя способами матрицы

 

 

1
7 0 9 1
1 2 3
1 1

 
2 4 8 1 0
 4 5 6  ·  −1 1 

·
1 1 2 0 1
7 8 9
0 1
0
0 1 2 −1
Решение. Первый способ:

 

1 2 3
1
 4 5 6  ·  −1  =
7 8 9
0

0

1
.
0
0
Пример 5. Вычислить двумя способами матрицы

 

 

1
7 0 9 1
1 2 3
1 1

 
2 4 8 1 0
 4 5 6  ·  −1 1 

·
1 1 2 0 1
7 8 9
0 1
0
0 1 2 −1
Решение. Первый способ:

 

 
 
 
1 2 3
1
1
2
3
 4 5 6  ·  −1  = 1 ·  4  − 1 ·  5  + 0 ·  6  =
7 8 9
0
7
8
9

0

1
.
0
0
Пример 5. Вычислить двумя способами матрицы

 

 

1
7 0 9 1
1 2 3
1 1

 
2 4 8 1 0
 4 5 6  ·  −1 1 

·
1 1 2 0 1
7 8 9
0 1
0
0 1 2 −1

0

1
.
0
0
Решение. Первый способ

 

 
 
  

1 2 3
1
1
2
3
−1
 4 5 6  ·  −1  = 1 ·  4  − 1 ·  5  + 0 ·  6  =  −1  .
7 8 9
0
7
8
9
−1
Пример 5. Вычислить двумя способами матрицы

 

 

1
7 0 9 1
1 2 3
1 1

 
2 4 8 1 0
 4 5 6  ·  −1 1 

·
1 1 2 0 1
7 8 9
0 1
0
0 1 2 −1

0

1
.
0
0
Решение. Первый способ

1 2 3
 4 5 6
7 8 9

1 2
 4 5
7 8
 

 
 
  

1
1
2
3
−1
 ·  −1  = 1 ·  4  − 1 ·  5  + 0 ·  6  =  −1  .
0
7
8
9
−1
  
3
1


6
1 =
·
9
1
Пример 5. Вычислить двумя способами матрицы

 

 

1
7 0 9 1
1 2 3
1 1

 
2 4 8 1 0
 4 5 6  ·  −1 1 

·
1 1 2 0 1
7 8 9
0 1
0
0 1 2 −1

0

1
.
0
0
Решение. Первый способ

1 2 3
 4 5 6
7 8 9

1 2
 4 5
7 8
 


1
 ·  −1  = 1 · 
0
  

3
1
6  ·  1  = 1
9
1

 

1
2
4 −1· 5 +0·
7
8

 

1
2
3




4
· +1 5
+1 6
7
8
9
 

3
−1
6  =  −1  .
9
−1

=
Пример 5. Вычислить двумя способами матрицы

 

 

1
7 0 9 1
1 2 3
1 1

 
2 4 8 1 0
 4 5 6  ·  −1 1 

·
1 1 2 0 1
7 8 9
0 1
0
0 1 2 −1

0

1
.
0
0
Решение. Первый способ

1 2 3
 4 5 6
7 8 9

1 2
 4 5
7 8
 


1
 ·  −1  = 1 · 
0
  

3
1
6  ·  1  = 1
9
1

 

1
2
4 −1· 5 +0·
7
8

 

1
2
3




4
· +1 5
+1 6
7
8
9
 

3
−1
6  =  −1  .
9
−1
 

6
 =  15  .
24
Пример 5. Вычислить двумя способами матрицы

 

 

1
7 0 9 1
1 2 3
1 1

 
2 4 8 1 0
 4 5 6  ·  −1 1 

·
1 1 2 0 1
7 8 9
0 1
0
0 1 2 −1

0

1
.
0
0
Решение. Первый способ

Таким
 

 
 
  

1
1
2
3
−1
 ·  −1  = 1 ·  4  − 1 ·  5  + 0 ·  6  =  −1  .
0
7
8
9
−1
  
 
 
  

3
1
1
2
3
6
6  ·  1  = 1  4  · +1  5  + 1  6  =  15  .
9
1
7
8
9
24


 
 
1 2 3
1 1
−1 6
образом,  4 5 6  ·  −1 1  =  −1 15 .
−1 24
7 8 9
0 1
1 2 3
 4 5 6
7 8 9

1 2
 4 5
7 8
Пример 5. Вычислить двумя способами матрицы

 

 

1
7 0 9 1
1 2 3
1 1

 
2 4 8 1 0
 4 5 6  ·  −1 1 

·
1 1 2 0 1
7 8 9
0 1
0
0 1 2 −1
Решение. Второй способ:


1
1
1 2 3 ·  −1 1  =
0 1

0

1
.
0
0
Пример 5. Вычислить двумя способами матрицы

 

 

1
7 0 9 1
1 2 3
1 1

 
2 4 8 1 0
 4 5 6  ·  −1 1 

·
1 1 2 0 1
7 8 9
0 1
0
0 1 2 −1
Решение. Второй способ:


1
1
1 2 3 ·  −1 1  = 1
0 1
1 1
+2
−1 1
+3
0 1
=

0

1
.
0
0
Пример 5. Вычислить двумя способами матрицы

 

 

1
7 0 9 1
1 2 3
1 1

 
2 4 8 1 0
 4 5 6  ·  −1 1 

·
1 1 2 0 1
7 8 9
0 1
0
0 1 2 −1

0

1
.
0
0
Решение. Второй способ:


1
1
1 2 3 ·  −1 1  = 1
0 1
1 1
+2
−1 1
+3
0 1
=
−1 6
.
Пример 5. Вычислить двумя способами матрицы

 

 

1
7 0 9 1
1 2 3
1 1

 
2 4 8 1 0
 4 5 6  ·  −1 1 

·
1 1 2 0 1
7 8 9
0 1
0
0 1 2 −1

0

1
.
0
0
Решение. Второй способ:


1
1
1 2 3 ·  −1 1  = 1
0 1


1 1
4 5 6 ·  −1 1  =
0 1
1 1
+2
−1 1
+3
0 1
=
−1 6
.
Пример 5. Вычислить двумя способами матрицы

 

 

1
7 0 9 1
1 2 3
1 1

 
2 4 8 1 0
 4 5 6  ·  −1 1 

·
1 1 2 0 1
7 8 9
0 1
0
0 1 2 −1

0

1
.
0
0
Решение. Второй способ:


1
1
1 2 3 ·  −1 1  = 1 1 1 + 2 −1 1 + 3 0 1 =
0 1


1 1
4 5 6 ·  −1 1  = 4 1 1 + 5 −1 1 + 6 0 1 =
0 1
−1 6
.
Пример 5. Вычислить двумя способами матрицы

 

 

1
7 0 9 1
1 2 3
1 1

 
2 4 8 1 0
 4 5 6  ·  −1 1 

·
1 1 2 0 1
7 8 9
0 1
0
0 1 2 −1

0

1
.
0
0
Решение. Второй способ:


1
1
1 2 3 ·  −1 1  = 1 1 1 + 2 −1 1 + 3 0 1 = −1 6 .
0 1


1 1
4 5 6 ·  −1 1  = 4 1 1 + 5 −1 1 + 6 0 1 = −1 15 .
0 1
Пример 5. Вычислить двумя способами матрицы

 

 

1
7 0 9 1
1 2 3
1 1

 
2 4 8 1 0
 4 5 6  ·  −1 1 

·
1 1 2 0 1
7 8 9
0 1
0
0 1 2 −1

0

1
.
0
0
Решение. Второй способ:


1
1
1 2 3 ·  −1 1  = 1 1 1 + 2 −1 1 + 3 0 1 = −1 6 .
0 1


1 1
4 5 6 ·  −1 1  = 4 1 1 + 5 −1 1 + 6 0 1 = −1 15 .
0 1


1
1
7 8 9 ·  −1 1  =
0 1
Пример 5. Вычислить двумя способами матрицы

 

 

1
7 0 9 1
1 2 3
1 1

 
2 4 8 1 0
 4 5 6  ·  −1 1 

·
1 1 2 0 1
7 8 9
0 1
0
0 1 2 −1

0

1
.
0
0
Решение. Второй способ:


1
1
1 2 3 ·  −1 1  = 1 1 1 + 2 −1 1 + 3 0 1 = −1 6 .
0 1


1 1
4 5 6 ·  −1 1  = 4 1 1 + 5 −1 1 + 6 0 1 = −1 15 .
0 1


1
1
7 8 9 ·  −1 1  = 7 1 1 + 8 −1 1 + 9 0 1 =
0 1
Пример 5. Вычислить двумя способами матрицы

 

 

1
7 0 9 1
1 2 3
1 1

 
2 4 8 1 0
 4 5 6  ·  −1 1 

·
1 1 2 0 1
7 8 9
0 1
0
0 1 2 −1

0

1
.
0
0
Решение. Второй способ:


1
1
1 2 3 ·  −1 1  = 1 1 1 + 2 −1 1 + 3 0 1 = −1 6 .
0 1


1 1
4 5 6 ·  −1 1  = 4 1 1 + 5 −1 1 + 6 0 1 = −1 15 .
0 1


1
1
7 8 9 ·  −1 1  = 7 1 1 + 8 −1 1 + 9 0 1 = −1 24 .
0 1
Пример 5. Вычислить двумя способами матрицы

 

 

1
7 0 9 1
1 2 3
1 1

 
2 4 8 1 0
 4 5 6  ·  −1 1 

·
1 1 2 0 1
7 8 9
0 1
0
0 1 2 −1
Решение.

 
 

1 2 3
1 1
−1 6
Следовательно,  4 5 6  ·  −1 1  =  −1 15 .
7 8 9
0 1
−1 24

0

1
.
0
0
Пример 5. Вычислить двумя способами матрицы

 

 

1
7 0 9 1
1 2 3
1 1

 
2 4 8 1 0
 4 5 6  ·  −1 1 

·
1 1 2 0 1
7 8 9
0 1
0
0 1 2 −1
Решение. Для второго произведения имеем:

0

1
.
0
0
Пример 5. Вычислить двумя способами матрицы

 

 

1
7 0 9 1
1 2 3
1 1

 
2 4 8 1 0
 4 5 6  ·  −1 1 

·
1 1 2 0 1
7 8 9
0 1
0
0 1 2 −1
Решение. Для второго произведения имеем:

7
 2

 1
0
0
4
1
1
 
9
1
1 0
 0 1
8
1 
·
2
0   1 0
2 −1
0 0


=


0

1
.
0
0
Пример 5. Вычислить двумя способами матрицы

 

 

1
7 0 9 1
1 2 3
1 1

 
2 4 8 1 0
 4 5 6  ·  −1 1 

·
1 1 2 0 1
7 8 9
0 1
0
0 1 2 −1
Решение. Для второго произведения имеем:

7
 2

 1
0
0
4
1
1
 
9
1
1 0
 0 1
8
1 
·
2
0   1 0
2 −1
0 0


=


0

1
.
0
0
Пример 5. Вычислить двумя способами матрицы

 

 

1
7 0 9 1
1 2 3
1 1

 
2 4 8 1 0
 4 5 6  ·  −1 1 

·
1 1 2 0 1
7 8 9
0 1
0
0 1 2 −1
Решение. Для второго произведения имеем:

7
 2

 1
0
0
4
1
1
 
9
1
1 0
 0 1
8
1 
·
2
0   1 0
2 −1
0 0


16
  10
=
  3
2





0

1
.
0
0
Пример 5. Вычислить двумя способами матрицы

 

 

1
7 0 9 1
1 2 3
1 1

 
2 4 8 1 0
 4 5 6  ·  −1 1 

·
1 1 2 0 1
7 8 9
0 1
0
0 1 2 −1
Решение. Для второго произведения имеем:

7
 2

 1
0
0
4
1
1
 
9
1
1 0
 0 1
8
1 
·
2
0   1 0
2 −1
0 0


16
  10
=
  3
2





0

1
.
0
0
Пример 5. Вычислить двумя способами матрицы

 

 

1
7 0 9 1
1 2 3
1 1

 
2 4 8 1 0
 4 5 6  ·  −1 1 

·
1 1 2 0 1
7 8 9
0 1
0
0 1 2 −1
Решение. Для второго произведения имеем:

7
 2

 1
0
0
4
1
1
 
9
1
1 0
 0 1
8
1 
·
2
0   1 0
2 −1
0 0


16
  10
=
  3
2





0

1
.
0
0
Пример 5. Вычислить двумя способами матрицы

 

 

1
7 0 9 1
1 2 3
1 1

 
2 4 8 1 0
 4 5 6  ·  −1 1 

·
1 1 2 0 1
7 8 9
0 1
0
0 1 2 −1
Решение. Для второго произведения имеем:

7
 2

 1
0
0
4
1
1
 
9
1
1 0
 0 1
8
1 
·
2
0   1 0
2 −1
0 0


16
  10
=
  3
2

0
4 

1 
1

0

1
.
0
0
Пример 5. Вычислить двумя способами матрицы

 

 

1
7 0 9 1
1 2 3
1 1

 
2 4 8 1 0
 4 5 6  ·  −1 1 

·
1 1 2 0 1
7 8 9
0 1
0
0 1 2 −1
Решение. Для второго произведения имеем:

7
 2

 1
0
0
4
1
1
 
9
1
1 0
 0 1
8
1 
·
2
0   1 0
2 −1
0 0


16
  10
=
  3
2

0
4 

1 
1
Вернуться к лекции «умножение на макроуровне»?

0

1
.
0
0
Пример 6 (к доказательству критерия
 обратимости
 матрицы).
−1 2 −1
Найти матрицу, обратную к A =  2 2 1 .
−2 −1 3
Решение. Вычислим дополнительные миноры элементов:
Пример 6 (к доказательству критерия
 обратимости
 матрицы).
−1 2 −1
Найти матрицу, обратную к A =  2 2 1 .
−2 −1 3
Решение. Вычислим дополнительные миноры элементов:
M11
−1
2 −1 2
1 = 7,
= 2
−2 −1
3 Пример 6 (к доказательству критерия
 обратимости
 матрицы).
−1 2 −1
Найти матрицу, обратную к A =  2 2 1 .
−2 −1 3
Решение. Вычислим дополнительные миноры элементов:
M11
−1
2 −1 2
1 = 7,
= 2
−2 −1
3 M12
−1
2 −1 2
1 = 8,
= 2
−2 −1
3 Пример 6 (к доказательству критерия
 обратимости
 матрицы).
−1 2 −1
Найти матрицу, обратную к A =  2 2 1 .
−2 −1 3
Решение. Вычислим дополнительные миноры элементов:
M11
−1
2 −1 2
1 = 7,
= 2
−2 −1
3 M12
−1
2 −1 2
1 = 8,
= 2
−2 −1
3 M13
−1
2 −1 2
1 = 2,
= 2
−2 −1
3 Пример 6 (к доказательству критерия
 обратимости
 матрицы).
−1 2 −1
Найти матрицу, обратную к A =  2 2 1 .
−2 −1 3
Решение. Вычислим дополнительные миноры элементов:
M11
M21
M31
−1
2 −1 2
1 = 7,
= 2
−2 −1
3 −1
2 −1 2
1 = 5,
= 2
−2 −1
3 −1
2
−1
2
1 = 4,
= 2
−2 −1
3 M12
M22
M32
−1
2 −1 2
1 = 8,
= 2
M13 = −2 −1
3 −1
2 −1 2
1 = −5, M23 = = 2
−2 −1
3 −1
2
−1
2
1 = 1,
= 2
M33 = −2 −1
3 −1
2 −1 2
2
1 = 2,
−2 −1
3 −1
2 −1 2
2
1 = 5,
−2 −1
3 −1
2 −1 2
2
1 = −6,
−2 −1
3 M11
M21
M31
−1
2 −1 2
1 = 7,
= 2
−2 −1
3 −1
2
−1
2
1 = 5,
= 2
−2 −1
3 −1
2
−1
2
1 = 4,
= 2
−2 −1
3 M12
M22
M32
−1
2 −1 2
1 = 8,
= 2
M13 = −2 −1
3 −1
2
−1
2
1 = −5, M23 = = 2
−2 −1
3 −1
2
−1
2
1 = 1,
= 2
M33 = −2 −1
3 −1
2 −1 2
2
1 = 2,
−2 −1
3 −1
2 −1 2
2
1 = 5,
−2 −1
3 −1
2 −1 2
2
1 = −6,
−2 −1
3 Выпишем
матрицу

 из полученных дополнительных миноров элемен7 8 2
тов:  5 −5 5 .
4 1 −6
Пример 6 (к доказательству критерия
 обратимости
 матрицы).
−1 2 −1
Найти матрицу, обратную к A =  2 2 1 .
−2 −1 3
Решение. Выпишем
матрицуиз полученных дополнительных ми
7 8 2
норов элементов:  5 −5 5 .
4 1 −6
Теперь, чтобы получить матрицу из алгебраических дополнений,
поменяем знаки у соответствующих элементов:
Пример 6 (к доказательству критерия
 обратимости
 матрицы).
−1 2 −1
Найти матрицу, обратную к A =  2 2 1 .
−2 −1 3
Решение. Выпишем
матрицуиз полученных дополнительных ми
7 8 2
норов элементов:  5 −5 5 .
4 1 −6
Теперь, чтобы получить матрицу из алгебраических
дополнений,


7 −8 2
поменяем знаки у соответствующих элементов:  −5 −5 −5 .
4 −1 −6
Пример 6 (к доказательству критерия
 обратимости
 матрицы).
−1 2 −1
Найти матрицу, обратную к A =  2 2 1 .
−2 −1 3
Решение. Мы получили матрицу из алгебраических
 дополнений,

7 −8 2
поменяем знаки у соответствующих элементов:  −5 −5 −5 .
4 −1 −6
Чтобы получить присоединенную матрицу, необходимо последнюю
матрицу транспонировать:
Пример 6 (к доказательству критерия
 обратимости
 матрицы).
−1 2 −1
Найти матрицу, обратную к A =  2 2 1 .
−2 −1 3
Решение. Мы получили матрицу из алгебраических
 дополнений,

7 −8 2
поменяем знаки у соответствующих элементов:  −5 −5 −5 .
4 −1 −6
Чтобы получить присоединенную
последнюю
 матрицу, необходимо

7 −5 4
матрицу транспонировать: PA =  −8 −5 −1 .
2 −5 −6
Пример 6 (к доказательству критерия
 обратимости
 матрицы).
−1 2 −1
Найти матрицу, обратную к A =  2 2 1 .
−2 −1 3
Решение.
 Мы получили
 присоединенную матрицу:
7 −5 4
PA =  −8 −5 −1 .
2 −5 −6
Для получения обратной матрицы осталось найти детерминант
матрицы A. Это можно совместить с проверкой правильности вычисления матрицы PA. Дело в том, что компонетами i-го столбца
этой матрицы являются алгебраические дополнения к элементам
i-й строки матрицы A. Поэтому все элементы главной диагонали
матрицы A · PA равны детерминанту матрицы A.
Пример 6 (к доказательству критерия
 обратимости
 матрицы).
−1 2 −1
Найти матрицу, обратную к A =  2 2 1 .
−2 −1 3
Решение.
 Мы получили
 присоединенную матрицу:
7 −5 4
PA =  −8 −5 −1 .
2 −5 −6

 
 

−1 2 −1
7 −5 4
−25
...
 2 2 1  ·  −8 −5 −1  =  . . . −25 . . .  .
−2 −1 3
2 −5 −6
...
−25
Поэтому det A = −25. Кстати, если не полениться, и все-таки вычислить недиагональные элементы матрицы A · PA, они должны получиться равными 0. Но обычно такая проверка оказывается излишней.
Пример 6 (к доказательству критерия
 обратимости
 матрицы).
−1 2 −1
Найти матрицу, обратную к A =  2 2 1 .
−2 −1 3
Решение.



7 −5 4
PA =  −8 −5 −1  ,
2 −5 −6
A−1

−7 5 −4
1 
=
8 5 1 .
25
−2 5 6
Полезно было бы провести проверку правильности вычислений, то
есть убедиться в том, что AA−1 = E. Чаще для вычисления обратной
матрицы используется метод Гаусса.
Вернуться к лекции «критерий существования обратной матрицы» или рассмотреть другой пример?
Пример 7 (обратная
к матрице 2 × 2). Найти
a b
матрице A =
.
c d
Решение.
обратную
к
Пример 7 (обратная
к матрице 2 × 2). Найти
a b
матрице A =
.
c d
Решение. Присоединенная матрица имеет вид
обратную
к
Пример 7 (обратная
к матрице 2 × 2). Найти
a b
матрице A =
.
c d
обратную
Решение. Присоединенная матрица имеет вид PA =
поэтому
d −b
−c a
к
,
Пример 7 (обратная
к матрице 2 × 2). Найти
a b
матрице A =
.
c d
обратную
Решение. Присоединенная матрица имеет вид PA =
поэтому
−1
d −b
−c a
к
,
1
d −b
.
(1)
=
ad − bc −c a
Разумеется, при этом должно быть 0 6= ad − bc = det A.
Вернуться к лекции «критерий существования обратной матрицы»
a b
c d
Пример 8 (нахождения
обратной
матрицы). Найти матрицу,


1 2 1
обратную к A =  3 −1 2  .
3 1 3
Пример 8 (нахождения
обратной
матрицы). Найти матрицу,


1 2 1
обратную к A =  3 −1 2  .
3 1 3
Решение. Существует два способа найти обратную матрицу: с помощью присоединенной матрицы и с помощью метода Гаусса.
Пример 8 (нахождения
обратной
матрицы). Найти матрицу,


1 2 1
обратную к A =  3 −1 2  .
3 1 3


1 2 1
Решение. Найдем обратную матрицу к A =  3 −1 2  с помо3 1 3
щью присоединенной.
Пример 8 (нахождения
обратной
матрицы). Найти матрицу,


1 2 1
обратную к A =  3 −1 2  .
3 1 3


1 2 1
Решение. Найдем обратную матрицу к A =  3 −1 2  с помо3 1 3
щью присоединенной. Составим матрицу из дополнительных миноров элементов:
Пример 8 (нахождения
обратной
матрицы). Найти матрицу,


1 2 1
обратную к A =  3 −1 2  .
3 1 3


1 2 1
Решение. Найдем обратную матрицу к A =  3 −1 2  с помо3 1 3
щью присоединенной. Составим матрицу из дополнительных миноров
 элементов:
−5
−1 2 M
=
11
1 3 = −5


Пример 8 (нахождения
обратной
матрицы). Найти матрицу,


1 2 1
обратную к A =  3 −1 2  .
3 1 3


1 2 1
Решение. Найдем обратную матрицу к A =  3 −1 2  с помо3 1 3
щью присоединенной. Составим матрицу из дополнительных миноров
 элементов:
−5 3
3 2 M
=
12
3 3=3


Пример 8 (нахождения
обратной
матрицы). Найти матрицу,


1 2 1
обратную к A =  3 −1 2  .
3 1 3


1 2 1
Решение. Найдем обратную матрицу к A =  3 −1 2  с помо3 1 3
щью присоединенной. Составим матрицу из дополнительных миноров
 элементов:
−5 3 6
3 −1 M
=
13
3 1 =6


Пример 8 (нахождения
обратной
матрицы). Найти матрицу,


1 2 1
обратную к A =  3 −1 2  .
3 1 3


1 2 1
Решение. Найдем обратную матрицу к A =  3 −1 2  с помо3 1 3
щью присоединенной. Составим матрицу из дополнительных миноров
 элементов:
−5 3 6
2 1 M
=
21
1 3=5
 5

Пример 8 (нахождения
обратной
матрицы). Найти матрицу,


1 2 1
обратную к A =  3 −1 2  .
3 1 3


1 2 1
Решение. Найдем обратную матрицу к A =  3 −1 2  с помо3 1 3
щью присоединенной. Составим матрицу из дополнительных миноров
 элементов:
−5 3 6
1 1 M
=
22
3 3=0
 5 0

Пример 8 (нахождения
обратной
матрицы). Найти матрицу,


1 2 1
обратную к A =  3 −1 2  .
3 1 3


1 2 1
Решение. Найдем обратную матрицу к A =  3 −1 2  с помо3 1 3
щью присоединенной. Составим матрицу из дополнительных миноров
 элементов:
−5 3 6
1 2 M
=
23
3 1 = −5
 5 0 −5 
Пример 8 (нахождения
обратной
матрицы). Найти матрицу,


1 2 1
обратную к A =  3 −1 2  .
3 1 3


1 2 1
Решение. Найдем обратную матрицу к A =  3 −1 2  с помо3 1 3
щью присоединенной. Составим матрицу из дополнительных миноров
 элементов:
−5 3 6
2 1 M
=
31
−1 2 = 5
 5 0 −5 
5
Пример 8 (нахождения
обратной
матрицы). Найти матрицу,


1 2 1
обратную к A =  3 −1 2  .
3 1 3


1 2 1
Решение. Найдем обратную матрицу к A =  3 −1 2  с помо3 1 3
щью присоединенной. Составим матрицу из дополнительных миноров
 элементов:
−5 3 6
1 1 M
=
32
3 2 = −1
 5 0 −5 
5 −1
Пример 8 (нахождения
обратной
матрицы). Найти матрицу,


1 2 1
обратную к A =  3 −1 2  .
3 1 3


1 2 1
Решение. Найдем обратную матрицу к A =  3 −1 2  с помо3 1 3
щью присоединенной. Составим матрицу из дополнительных миноров
 элементов:
−5 3 6
1 2 M
=
33
3 −1 = −7
 5 0 −5 
5 −1 −7
Пример 8 (нахождения
обратной
матрицы). Найти матрицу,


1 2 1
обратную к A =  3 −1 2  .
3 1 3


1 2 1
Решение. Найдем обратную матрицу к A =  3 −1 2  с помо3 1 3
щью присоединенной. Сменим знаки в определенных местах, чтобы
получить
алгебраические
дополнения:


−5 3 6
 5 0 −5 
5 −1 −7
Пример 8 (нахождения
обратной
матрицы). Найти матрицу,


1 2 1
обратную к A =  3 −1 2  .
3 1 3


1 2 1
Решение. Найдем обратную матрицу к A =  3 −1 2  с помо3 1 3
щью присоединенной. Сменим знаки в определенных местах, чтобы
получить
алгебраические
дополнения:

 

−5 3 6
−5
6
 5 0 −5  

0
5 −1 −7
5
−7
Пример 8 (нахождения
обратной
матрицы). Найти матрицу,


1 2 1
обратную к A =  3 −1 2  .
3 1 3


1 2 1
Решение. Найдем обратную матрицу к A =  3 −1 2  с помо3 1 3
щью присоединенной. Сменим знаки в определенных местах, чтобы
получить
алгебраические
дополнения:

 

−5 3 6
−5 −3 6
 5 0 −5   −5 0 5 
5 −1 −7
5 1 −7
Пример 8 (нахождения
обратной
матрицы). Найти матрицу,


1 2 1
обратную к A =  3 −1 2  .
3 1 3


1 2 1
Решение. Найдем обратную матрицу к A =  3 −1 2  с помо3 1 3
щью присоединенной. Транспонируем матрицу, чтобы получить присоединенную:

 



−5 3 6
-5 −3 6
-5 -5 5
 5 0 −5   -5 0 5 

PA = 
5 −1 −7
5 1 −7
Пример 8 (нахождения
обратной
матрицы). Найти матрицу,


1 2 1
обратную к A =  3 −1 2  .
3 1 3


1 2 1
Решение. Найдем обратную матрицу к A =  3 −1 2  с помо3 1 3
щью присоединенной. Транспонируем матрицу, чтобы получить присоединенную:

 



−5 3 6
−5 -3 6
−5 −5 5
 5 0 −5   −5 0 5 
PA =  -3 0 1 
5 −1 −7
5 1 −7
Пример 8 (нахождения
обратной
матрицы). Найти матрицу,


1 2 1
обратную к A =  3 −1 2  .
3 1 3


1 2 1
Решение. Найдем обратную матрицу к A =  3 −1 2  с помо3 1 3
щью присоединенной. Транспонируем матрицу, чтобы получить присоединенную:

 



−5 3 6
−5 −3 6
−5 −5 5
 5 0 −5   −5 0 5 
PA =  −3 0 1 
5 −1 −7
5 1 -7
6 5 -7
Пример 8 (нахождения
обратной
матрицы). Найти матрицу,


1 2 1
обратную к A =  3 −1 2  .
3 1 3


1 2 1
Решение. Найдем обратную матрицу к A =  3 −1 2  с помо3 1 3
щью присоединенной. Найдем детерминант матрицы A. Элементами
присоединенной матрицы являются алгебраические дополнения, поэтому найдем детерминант A по теореме о разложении детерминанта по строке или столбцу.


−5 −5 5
PA =  −3 0 1 
6 5 −7
Пример 8 (нахождения
обратной
матрицы). Найти матрицу,


1 2 1
обратную к A =  3 −1 2  .
3 1 3


1 2 1
Решение. Найдем обратную матрицу к A =  3 −1 2  с помо3 1 3
щью присоединенной. Найдем детерминант матрицы A. Элементами
присоединенной матрицы являются алгебраические дополнения, поэтому найдем детерминант A по теореме о разложении детерминанта по строке или столбцу.


detA = 1 · (−5) + 2 · (−3) + 1 · 6 = −5,
−5 −5 5
PA =  −3 0 1 
6 5 −7
Пример 8 (нахождения
обратной
матрицы). Найти матрицу,


1 2 1
обратную к A =  3 −1 2  .
3 1 3


1 2 1
Решение. Найдем обратную матрицу к A =  3 −1 2  с помо3 1 3
щью присоединенной. Найдем детерминант матрицы A. Элементами
присоединенной матрицы являются алгебраические дополнения, поэтому найдем детерминант A по теореме о разложении детерминанта по строке или столбцу.


detA = 1 · (−5) + 2 · (−3) + 1 · 6 = −5,
−5 −5 5
PA =  −3 0 1 
detA = 3 · (−5) + (−1) · 0 + 2 · 5 = −5,
6 5 −7
Пример 8 (нахождения
обратной
матрицы). Найти матрицу,


1 2 1
обратную к A =  3 −1 2  .
3 1 3


1 2 1
Решение. Найдем обратную матрицу к A =  3 −1 2  с помо3 1 3
щью присоединенной. Найдем детерминант матрицы A. Элементами
присоединенной матрицы являются алгебраические дополнения, поэтому найдем детерминант A по теореме о разложении детерминанта по строке или столбцу.


detA = 1 · (−5) + 2 · (−3) + 1 · 6 = −5,
−5 −5 5
PA =  −3 0 1 
detA = 3 · (−5) + (−1) · 0 + 2 · 5 = −5,
detA = 3 · 5 + 1 · 1 + 3 · (−7) = −5
6 5 −7
Пример 8 (нахождения
обратной
матрицы). Найти матрицу,


1 2 1
обратную к A =  3 −1 2  .
3 1 3


1 2 1
Решение. Найдем обратную матрицу к A =  3 −1 2  с помо3 1 3
щью присоединенной. Из критерия обратимости квадратной матрицы:


−5 −5 5
detA = −5, PA =  −3 0 1 
6 5 −7
Пример 8 (нахождения
обратной
матрицы). Найти матрицу,


1 2 1
обратную к A =  3 −1 2  .
3 1 3


1 2 1
Решение. Найдем обратную матрицу к A =  3 −1 2  с помо3 1 3
щью присоединенной. Из критерия обратимости квадратной матрицы:




−5 −5 5
−5 −5 5
1
A−1 = −  −3 0 1  detA = −5, PA =  −3 0 1 
5
6 5 −7
6 5 −7
Пример 8 (нахождения
обратной
матрицы). Найти матрицу,


1 2 1
обратную к A =  3 −1 2  .
3 1 3
Решение. Найдем матрицу, обратную к A, методом Гаусса.
Пример 8 (нахождения
обратной
матрицы). Найти матрицу,


1 2 1
обратную к A =  3 −1 2  .
3 1 3
Решение.
Найдем матрицу,
обратную к A, методом Гаусса.


1 2 1 1 0 0
 3 −1 2 0 1 0  ∼ Домножим первую строку на −3 и сложим
3 1 3 0 0 1
со второй и третьей, первую строку запишем в первоначальном виде.
Пример 8 (нахождения
обратной
матрицы). Найти матрицу,


1 2 1
обратную к A =  3 −1 2  .
3 1 3
Решение.
Найдем матрицу,
Гаусса.

  обратную к A, методом

1 2 1 1 0 0
1 2 1 1 0 0
 3 −1 2 0 1 0  ∼  0 −7 −1 −3 1 0  ∼ Домножим вто3 1 3 0 0 1
0 −5 0 −3 0 1
рую строку на −5, а третью на 7.
Пример 8 (нахождения
обратной
матрицы). Найти матрицу,


1 2 1
обратную к A =  3 −1 2  .
3 1 3
Решение.
Найдем матрицу,

  обратную к A методом
 Гаусса.
1 2 1 1 0 0
1 2 1 1 0 0
 3 −1 2 0 1 0  ∼  0 −7 −1 −3 1 0  ∼
3 1 3 0 0 1
0 −5 0 −3 0 1


0 0
1 2 1 1
∼  0 35 5 15 −5 0  ∼
0 −35 0 −21 0 7
Пример 8 (нахождения
обратной
матрицы). Найти матрицу,


1 2 1
обратную к A =  3 −1 2  .
3 1 3
Решение. Найдем матрицу, обратную к A методом Гаусса.
Сложим
вторую и 
третью

 строки:

1 2 1 1 0 0
1 2 1 1 0 0
 3 −1 2 0 1 0  ∼  0 −7 −1 −3 1 0  ∼
3 1 3 0 0 1
0 −5 0 −3 0 1

 

1 2 1 1
1 2 1 1 0 0
0 0
∼  0 35 5 15 −5 0  ∼  0 −7 −1 −3 1 0  ∼
0 −35 0 −21 0 7
0 0 5 −6 −5 7
Пример 8 (нахождения
обратной
матрицы). Найти матрицу,


1 2 1
обратную к A =  3 −1 2  .
3 1 3
Решение.
Найдем матрицу,
к A методом Гаусса.

 обратную


1 2 1 1
0 0
1 2 1 1 0 0
 0 35 5 15 −5 0  ∼  0 −7 −1 −3 1 0  ∼
0 0 5 −6 −5 7
 0 −35 0 −21 0 7 
1 2 1 1 0 0
 0 −7 −1 −3 1 0 
∼
∼

7
6
0 0 1 − −1
5
5
Пример 8 (нахождения
обратной
матрицы). Найти матрицу,


1 2 1
обратную к A =  3 −1 2  .
3 1 3
Решение.
Найдем матрицу,
к A методом Гаусса.

 обратную


1 2 1 1
0 0
1 2 1 1 0 0
 0 35 5 15 −5 0  ∼  0 −7 −1 −3 1 0  ∼
0 −35 0 −21 0 7
0 0 5 −6 −5 7 
 

1 −5 0 −2 1 0
1 2 1 1 0 0

 0 −7 −1 −3 1 0  
 0 −7 0 − 21 0 7 


∼
∼
∼
5
5
6
7 

6
7
0 0 1 − −1
0
0
1
−
−1
5
5
5
5
Пример 8 (нахождения
обратной
матрицы). Найти матрицу,


1 2 1
обратную к A =  3 −1 2  .
3 1 3
Решение. Найдем матрицу, обратную
к A методом Гаусса.


 
1 −5 0 −2 1 0
1 2 1 1 0 0
21
7
 0 −7 −1 −3 1 0  


0
 ∼  0 −7 0 −
∼
∼
5
5

6
7 

6
7
0 0 1 − −1
0
0
1
−
−1
5
5
5
5


7 −7
7 0 0 7


 0 −7 0 − 21 0 7 
∼
∼
5
5 


6
7
0 0 1 − −1
5
5
Пример 8 (нахождения
обратной
матрицы). Найти матрицу,


1 2 1
обратную к A =  3 −1 2  .
3 1 3
Решение. Найдем матрицу, обратную
к A методом Гаусса.


 
1 −5 0 −2 1 0
1 2 1 1 0 0
21
7
 0 −7 −1 −3 1 0  


0
 ∼  0 −7 0 −
∼
∼
5
5

6
7 

6
7
0 0 1 − −1
0
0
1
−
−1
5
5
5
5
 


7 −7
1 0 0 1 1 −1
7 0 0 7




 0 −7 0 − 21 0 7   0 1 0 3 0 − 1 
∼
∼
5
5 
5
5



6
7
6
7 
0 0 1 − −1
0 0 1 − −1
5
5
5
5
Пример 8 (нахождения
обратной
матрицы). Найти матрицу,


1 2 1
обратную к A =  3 −1 2  .
3 1 3
Решение.
Найдем матрицу, обратную
  к A методом Гаусса.


7 0 0 7
7 −7
1 0 0 1 1 −1

 

 0 −7 0 − 21 0 7   0 1 0 3 0 − 1 
∼
∼
5
5 
5
5



6
6
7
7 
0 0 1 − −1
0 0 1 − −1
5
5
5
5


1 1 −1
 3
1


A−1 =  5 0 − 5 
 6
7 
− −1
5
5
Вернуться к лекции?
Задача I.1. (Ответ приведен на стр.159.) Записать формулу для вычисления произведения матриц X2×3 и Y3×5.
Задача I.2. (Ответ приведен на стр.174.) Для матриц Fm×n, Gn×m и
Hm×m запишите формулы для вычисления коэффициентов матриц
A = FG, B = GF, C = FtH, D = HGt.
Задача I.3. (Ответ приведен на стр.194.) Для матриц Fn×m, Gm×m и
Hm×m запишите формулы для вычисления коэффициентов матриц
A = F (G + H), B = FGH, C = GHFt, D = FHtFt.
Задача II.4.
(Ответ
приведен
на стр.225.) 2 5
3 1
−3 1
−1 1




−2 0 1 −1
2 −1 2
−1
3 −1 0 
2 1 1 0  =?,  2 3 1   3
1 0 −1
1 0 0 1
2 −1 1
−2
произведения
матриц:
Найдите
0 1
=?,
1 −1

2
1  =?.
1
Задача III.5.
(Ответ приведен на стр.229.)

на x2 − 2x − 4
Вычислить
значение многочле
2 −1 2
при x =  1 −1 0 .
3 −1 1
Задача IV.6. (Ответ приведен на стр.238.) С помощью умножения матриц
подберите
матрицы X и Y с тем, чтобы
 «на макроуровне»



1 2 3
1 −1
X  4 5 6  Y =  4 −4 .
7 8 9
7 −7
Задача IV.7. (Ответ приведен на стр.250.) С помощью умножения матриц
подберите матрицы X и Y с тем, чтобы
 «на макроуровне»

1 2 3
4 −4
X  4 5 6 Y =
.
7 −7
7 8 9
Задача IV.8. (Ответ приведен на стр.253.)
С помощью умножения
матриц «намакроуровне» сведите решение
трех систем линейных
x − y = 1,
a − b = 2,
α − β = 0,
уравнений:
к одному
x + y = −1,
a + b = 2,
α + β = 2,
матричному уравнению.
Задача IV.9. (Ответ приведен на стр.261.) Функцию, вычисляющую сумму
всех элементов матрицы размерности 3 × 2, определить формулой,
использующей только умножение матриц и детерминант.
Задача V.10.
на стр.263.)
Следует ли из равенства

 (Ответ приведен
−2 3
1
0
1
−1
2
1 −1 2 
, что матрицы
и
1 −1  =
1 0 1
0 1
1 0 1
2 −2


−2 3
 1 −1  — обратные друг к другу?
2 −2
Задача V.11. (Ответ приведен на стр.265.) Как из матрицы A−1 размерности 3 × 3 получить матрицу B −1, если B получена из A перестановкой
первой и третьей строк?
Задача V.12.(Ответ приведен
на стр.271.) Найдите матрицу, обратную к
1 2
матрице A =
.
−3 −4
Задача V.13.
(Ответ приведен на стр.301.)
цы, обратную к матрицам A =


−8 28 −9 −15


 −12 32 −1 −15 
C=
.
 −20 40 −5 −15 
16 −36 8 20
0 −5
2 25
,
Вычислите
матри

−1 2 −3
B =  −1 2 −1 ,
−2 5 −1
Задача
на стр.305.)
матричные
уравне VI.14. (Ответ приведен
Решите 2 −1
1 −1
2 −1
1 −1
ния:
X=
, Y
=
,
−3 1
2 −2
−3 1
2 −2
2 −1
3 −2
−13 −6
Z
=
,
−3 1
4 1
18 10
2 3
1 −2 5
T =
.
−3 −4
3 4 −1
Задача
VI.15. 
(Ответ приведен на стр.352.) Решите матричное уравнение



8 −3 −3
2 0 −3
X ·  1 −1 1  =  −3 1 2 
1 0 0
7 0 −6
VI.16.(Ответ приведен
Решите матричное
уравнение
 на стр.354.)


Задача
3 −1 2
60 −4 40
1 2 3
 4 5 6  X ·  1 1 1  =  123 −7 82  .
7 8 9
2 0 1
186 −10 124
Ответы и решения
Решение задачи 1.
Задача 1. Записать формулу для вычисления произведения матриц X2×3 и Y3×5 .
Задача 1. Записать формулу для вычисления произведения матриц X2×3 и Y3×5 .
Ответ.
zij = x y + x y + x y
Задача 1. Записать формулу для вычисления произведения матриц X2×3 и Y3×5 .
Ответ.
zij = x y + x y + x y
Задача 1. Записать формулу для вычисления произведения матриц X2×3 и Y3×5 .
Ответ.
zij = xi y + xi y + xi y
Задача 1. Записать формулу для вычисления произведения матриц X2×3 и Y3×5 .
Ответ.
zij = xi y + xi y + xi y
Задача 1. Записать формулу для вычисления произведения матриц X2×3 и Y3×5 .
Ответ.
zij = xi y j + xi y j + xi y
j
Задача 1. Записать формулу для вычисления произведения матриц X2×3 и Y3×5 .
Ответ.
zij = xi1 y1j + xi y j + xi y
j
Задача 1. Записать формулу для вычисления произведения матриц X2×3 и Y3×5 .
Ответ.
zij = xi1 y1j + xi2 y2j + xi y
j
Задача 1. Записать формулу для вычисления произведения матриц X2×3 и Y3×5 .
Ответ.
zij = xi1 y1j + xi2 y2j + xi3 y3j
Задача 1. Записать формулу для вычисления произведения матриц X2×3 и Y3×5 .
Ответ.
X
zij = xi1 y1j + xi2 y2j + xi3 y3j =
x y .
Задача 1. Записать формулу для вычисления произведения матриц X2×3 и Y3×5 .
Ответ.
X
zij = xi1 y1j + xi2 y2j + xi3 y3j =
x y .
Задача 1. Записать формулу для вычисления произведения матриц X2×3 и Y3×5 .
Ответ.
X
zij = xi1 y1j + xi2 y2j + xi3 y3j =
xi y .
Задача 1. Записать формулу для вычисления произведения матриц X2×3 и Y3×5 .
Ответ.
X
zij = xi1 y1j + xi2 y2j + xi3 y3j =
xi y j .
Задача 1. Записать формулу для вычисления произведения матриц X2×3 и Y3×5 .
Ответ.
X
zij = xi1 y1j + xi2 y2j + xi3 y3j =
xi y j .
Задача 1. Записать формулу для вычисления произведения матриц X2×3 и Y3×5 .
Ответ.
3
X
xik ykj .
zij = xi1 y1j + xi2 y2j + xi3 y3j =
k=1
Решение задачи 2.
Задача 2. Для матриц Fm×n , Gn×m и Hm×m запишите формулы для вычисления коэффициентов матриц A = FG, B = GF, C = Ft H, D = HGt .
Задача 2. Для матриц Fm×n , Gn×m и Hm×m запишите формулы для вычисления коэффициентов матриц A = FG, B = GF, C = Ft H, D = HGt .
Ответ. aij =
Задача 2. Для матриц Fm×n , Gn×m и Hm×m запишите формулы для вычисления коэффициентов матриц A = FG, B = GF, C = Ft H, D = HGt .
P
Ответ. aij =
f g ;
Задача 2. Для матриц Fm×n , Gn×m и Hm×m запишите формулы для вычисления коэффициентов матриц A = FG, B = GF, C = Ft H, D = HGt .
P
Ответ. aij =
fi g j ;
Задача 2. Для матриц Fm×n , Gn×m и Hm×m запишите формулы для вычисления коэффициентов матриц A = FG, B = GF, C = Ft H, D = HGt .
P
fik gkj ;
Ответ. aij =
k=1
Задача 2. Для матриц Fm×n , Gn×m и Hm×m запишите формулы для вычисления коэффициентов матриц A = FG, B = GF, C = Ft H, D = HGt .
n
P
fik gkj ;
Ответ. aij =
k=1
Задача 2. Для матриц Fm×n , Gn×m и Hm×m запишите формулы для вычисления коэффициентов матриц A = FG, B = GF, C = Ft H, D = HGt .
n
P
fik gkj ;
Ответ. aij =
k=1
buv =
P
p=1
Задача 2. Для матриц Fm×n , Gn×m и Hm×m запишите формулы для вычисления коэффициентов матриц A = FG, B = GF, C = Ft H, D = HGt .
n
P
fik gkj ;
Ответ. aij =
k=1
buv =
P
p=1
g f ;
Задача 2. Для матриц Fm×n , Gn×m и Hm×m запишите формулы для вычисления коэффициентов матриц A = FG, B = GF, C = Ft H, D = HGt .
n
P
fik gkj ;
Ответ. aij =
k=1
buv =
P
p=1
gu f v ;
Задача 2. Для матриц Fm×n , Gn×m и Hm×m запишите формулы для вычисления коэффициентов матриц A = FG, B = GF, C = Ft H, D = HGt .
n
P
fik gkj ;
Ответ. aij =
k=1
buv =
P
p=1
gup fpv ;
Задача 2. Для матриц Fm×n , Gn×m и Hm×m запишите формулы для вычисления коэффициентов матриц A = FG, B = GF, C = Ft H, D = HGt .
n
P
fik gkj ;
Ответ. aij =
buv =
m
P
p=1
k=1
gup fpv ;
Задача 2. Для матриц Fm×n , Gn×m и Hm×m запишите формулы для вычисления коэффициентов матриц A = FG, B = GF, C = Ft H, D = HGt .
n
P
fik gkj ;
Ответ. aij =
buv =
m
P
p=1
cpq =
P
s=1
k=1
gup fpv ;
Задача 2. Для матриц Fm×n , Gn×m и Hm×m запишите формулы для вычисления коэффициентов матриц A = FG, B = GF, C = Ft H, D = HGt .
n
P
fik gkj ;
Ответ. aij =
buv =
m
P
k=1
gup fpv ;
p=1
cpq =
P
s=1
f ph q ;
Задача 2. Для матриц Fm×n , Gn×m и Hm×m запишите формулы для вычисления коэффициентов матриц A = FG, B = GF, C = Ft H, D = HGt .
n
P
fik gkj ;
Ответ. aij =
buv =
m
P
k=1
gup fpv ;
p=1
cpq =
P
s=1
fsp hsq ;
Задача 2. Для матриц Fm×n , Gn×m и Hm×m запишите формулы для вычисления коэффициентов матриц A = FG, B = GF, C = Ft H, D = HGt .
n
P
fik gkj ;
Ответ. aij =
buv =
cpq =
m
P
p=1
m
P
s=1
k=1
gup fpv ;
fsp hsq ;
Задача 2. Для матриц Fm×n , Gn×m и Hm×m запишите формулы для вычисления коэффициентов матриц A = FG, B = GF, C = Ft H, D = HGt .
n
P
fik gkj ;
Ответ. aij =
buv =
cpq =
m
P
p=1
m
P
s=1
dxy =
P
k=1
gup fpv ;
fsp hsq ;
Задача 2. Для матриц Fm×n , Gn×m и Hm×m запишите формулы для вычисления коэффициентов матриц A = FG, B = GF, C = Ft H, D = HGt .
n
P
fik gkj ;
Ответ. aij =
buv =
cpq =
k=1
m
P
p=1
m
P
gup fpv ;
fsp hsq ;
s=1
dxy =
P
z=1
Задача 2. Для матриц Fm×n , Gn×m и Hm×m запишите формулы для вычисления коэффициентов матриц A = FG, B = GF, C = Ft H, D = HGt .
n
P
fik gkj ;
Ответ. aij =
buv =
cpq =
k=1
m
P
p=1
m
P
gup fpv ;
fsp hsq ;
s=1
dxy =
P
z=1
hx gy .
Задача 2. Для матриц Fm×n , Gn×m и Hm×m запишите формулы для вычисления коэффициентов матриц A = FG, B = GF, C = Ft H, D = HGt .
n
P
fik gkj ;
Ответ. aij =
buv =
cpq =
k=1
m
P
p=1
m
P
gup fpv ;
fsp hsq ;
s=1
dxy =
P
z=1
hxz gyz .
Задача 2. Для матриц Fm×n , Gn×m и Hm×m запишите формулы для вычисления коэффициентов матриц A = FG, B = GF, C = Ft H, D = HGt .
n
P
fik gkj ;
Ответ. aij =
buv =
cpq =
dxy =
k=1
m
P
p=1
m
P
gup fpv ;
fsp hsq ;
s=1
m
P
z=1
hxz gyz .
Решение задачи 3.
Задача 3. Для матриц Fn×m , Gm×m и Hm×m запишите формулы для вычисления коэффициентов матриц A = F (G + H), B = FGH, C = GHFt , D = FHt Ft .
Задача 3. Для матриц Fn×m , Gm×m и Hm×m запишите формулы для вычисления коэффициентов матриц A = F (G + H), B = FGH, C = GHFt , D = FHt Ft .
Ответ. aij =
Задача 3. Для матриц Fn×m , Gm×m и Hm×m запишите формулы для вычисления коэффициентов матриц A = F (G + H), B = FGH, C = GHFt , D = FHt Ft .
P
f (g + h ) ;
Ответ. aij =
k=1
Задача 3. Для матриц Fn×m , Gm×m и Hm×m запишите формулы для вычисления коэффициентов матриц A = F (G + H), B = FGH, C = GHFt , D = FHt Ft .
P
fi (g + h ) ;
Ответ. aij =
k=1
Задача 3. Для матриц Fn×m , Gm×m и Hm×m запишите формулы для вычисления коэффициентов матриц A = F (G + H), B = FGH, C = GHFt , D = FHt Ft .
P
fi (g j + h j ) ;
Ответ. aij =
k=1
Задача 3. Для матриц Fn×m , Gm×m и Hm×m запишите формулы для вычисления коэффициентов матриц A = F (G + H), B = FGH, C = GHFt , D = FHt Ft .
P
fik (gkj + hkj ) ;
Ответ. aij =
k=1
Задача 3. Для матриц Fn×m , Gm×m и Hm×m запишите формулы для вычисления коэффициентов матриц A = F (G + H), B = FGH, C = GHFt , D = FHt Ft .
m
P
fik (gkj + hkj ) ;
Ответ. aij =
k=1
Задача 3. Для матриц Fn×m , Gm×m и Hm×m запишите формулы для вычисления коэффициентов матриц A = F (G + H), B = FGH, C = GHFt , D = FHt Ft .
m
P
fik (gkj + hkj ) ;
Ответ. aij =
k=1
buv =
Задача 3. Для матриц Fn×m , Gm×m и Hm×m запишите формулы для вычисления коэффициентов матриц A = F (G + H), B = FGH, C = GHFt , D = FHt Ft .
m
P
fik (gkj + hkj ) ;
Ответ. aij =
k=1
buv =
PP
p=1 q=1
Задача 3. Для матриц Fn×m , Gm×m и Hm×m запишите формулы для вычисления коэффициентов матриц A = F (G + H), B = FGH, C = GHFt , D = FHt Ft .
m
P
fik (gkj + hkj ) ;
Ответ. aij =
k=1
buv =
PP
p=1 q=1
f g h ;
Задача 3. Для матриц Fn×m , Gm×m и Hm×m запишите формулы для вычисления коэффициентов матриц A = F (G + H), B = FGH, C = GHFt , D = FHt Ft .
m
P
fik (gkj + hkj ) ;
Ответ. aij =
k=1
buv =
PP
p=1 q=1
fu g h ;
Задача 3. Для матриц Fn×m , Gm×m и Hm×m запишите формулы для вычисления коэффициентов матриц A = F (G + H), B = FGH, C = GHFt , D = FHt Ft .
m
P
fik (gkj + hkj ) ;
Ответ. aij =
k=1
buv =
PP
p=1 q=1
fu g h v ;
Задача 3. Для матриц Fn×m , Gm×m и Hm×m запишите формулы для вычисления коэффициентов матриц A = F (G + H), B = FGH, C = GHFt , D = FHt Ft .
m
P
fik (gkj + hkj ) ;
Ответ. aij =
k=1
buv =
PP
p=1 q=1
fup gp h v ;
Задача 3. Для матриц Fn×m , Gm×m и Hm×m запишите формулы для вычисления коэффициентов матриц A = F (G + H), B = FGH, C = GHFt , D = FHt Ft .
m
P
fik (gkj + hkj ) ;
Ответ. aij =
k=1
buv =
PP
p=1 q=1
fup gpq hqv ;
Задача 3. Для матриц Fn×m , Gm×m и Hm×m запишите формулы для вычисления коэффициентов матриц A = F (G + H), B = FGH, C = GHFt , D = FHt Ft .
m
P
fik (gkj + hkj ) ;
Ответ. aij =
buv =
m P
P
p=1 q=1
k=1
fup gpq hqv ;
Задача 3. Для матриц Fn×m , Gm×m и Hm×m запишите формулы для вычисления коэффициентов матриц A = F (G + H), B = FGH, C = GHFt , D = FHt Ft .
m
P
fik (gkj + hkj ) ;
Ответ. aij =
buv =
m P
m
P
p=1 q=1
k=1
fup gpq hqv ;
Задача 3. Для матриц Fn×m , Gm×m и Hm×m запишите формулы для вычисления коэффициентов матриц A = F (G + H), B = FGH, C = GHFt , D = FHt Ft .
m
P
fik (gkj + hkj ) ;
Ответ. aij =
buv =
m P
m
P
p=1 q=1
cxy =
k=1
fup gpq hqv ;
Задача 3. Для матриц Fn×m , Gm×m и Hm×m запишите формулы для вычисления коэффициентов матриц A = F (G + H), B = FGH, C = GHFt , D = FHt Ft .
m
P
fik (gkj + hkj ) ;
Ответ. aij =
buv =
m P
m
P
k=1
fup gpq hqv ;
p=1 q=1
cxy =
PP
p=1 q=1
g h f ;
Задача 3. Для матриц Fn×m , Gm×m и Hm×m запишите формулы для вычисления коэффициентов матриц A = F (G + H), B = FGH, C = GHFt , D = FHt Ft .
m
P
fik (gkj + hkj ) ;
Ответ. aij =
buv =
m P
m
P
k=1
fup gpq hqv ;
p=1 q=1
cxy =
PP
p=1 q=1
gx h f ;
Задача 3. Для матриц Fn×m , Gm×m и Hm×m запишите формулы для вычисления коэффициентов матриц A = F (G + H), B = FGH, C = GHFt , D = FHt Ft .
m
P
fik (gkj + hkj ) ;
Ответ. aij =
buv =
m P
m
P
k=1
fup gpq hqv ;
p=1 q=1
cxy =
PP
p=1 q=1
gx h fy ;
Задача 3. Для матриц Fn×m , Gm×m и Hm×m запишите формулы для вычисления коэффициентов матриц A = F (G + H), B = FGH, C = GHFt , D = FHt Ft .
m
P
fik (gkj + hkj ) ;
Ответ. aij =
buv =
m P
m
P
k=1
fup gpq hqv ;
p=1 q=1
cxy =
PP
p=1 q=1
gxp hp fy ;
Задача 3. Для матриц Fn×m , Gm×m и Hm×m запишите формулы для вычисления коэффициентов матриц A = F (G + H), B = FGH, C = GHFt , D = FHt Ft .
m
P
fik (gkj + hkj ) ;
Ответ. aij =
buv =
m P
m
P
k=1
fup gpq hqv ;
p=1 q=1
cxy =
PP
p=1 q=1
gxp hpq fyq ;
Задача 3. Для матриц Fn×m , Gm×m и Hm×m запишите формулы для вычисления коэффициентов матриц A = F (G + H), B = FGH, C = GHFt , D = FHt Ft .
m
P
fik (gkj + hkj ) ;
Ответ. aij =
buv =
cxy =
m P
m
P
p=1 q=1
m P
P
p=1 q=1
k=1
fup gpq hqv ;
gxp hpq fyq ;
Задача 3. Для матриц Fn×m , Gm×m и Hm×m запишите формулы для вычисления коэффициентов матриц A = F (G + H), B = FGH, C = GHFt , D = FHt Ft .
m
P
fik (gkj + hkj ) ;
Ответ. aij =
buv =
cxy =
m P
m
P
p=1 q=1
m P
m
P
p=1 q=1
k=1
fup gpq hqv ;
gxp hpq fyq ;
Задача 3. Для матриц Fn×m , Gm×m и Hm×m запишите формулы для вычисления коэффициентов матриц A = F (G + H), B = FGH, C = GHFt , D = FHt Ft .
m
P
fik (gkj + hkj ) ;
Ответ. aij =
buv =
cxy =
m P
m
P
p=1 q=1
m P
m
P
p=1 q=1
dxy =
k=1
fup gpq hqv ;
gxp hpq fyq ;
Задача 3. Для матриц Fn×m , Gm×m и Hm×m запишите формулы для вычисления коэффициентов матриц A = F (G + H), B = FGH, C = GHFt , D = FHt Ft .
m
P
fik (gkj + hkj ) ;
Ответ. aij =
buv =
cxy =
m P
m
P
p=1 q=1
m P
m
P
k=1
fup gpq hqv ;
gxp hpq fyq ;
p=1 q=1
dxy =
PP
p=1 q=1
f h f .
Задача 3. Для матриц Fn×m , Gm×m и Hm×m запишите формулы для вычисления коэффициентов матриц A = F (G + H), B = FGH, C = GHFt , D = FHt Ft .
m
P
fik (gkj + hkj ) ;
Ответ. aij =
buv =
cxy =
m P
m
P
p=1 q=1
m P
m
P
k=1
fup gpq hqv ;
gxp hpq fyq ;
p=1 q=1
dxy =
PP
p=1 q=1
fx h f y .
Задача 3. Для матриц Fn×m , Gm×m и Hm×m запишите формулы для вычисления коэффициентов матриц A = F (G + H), B = FGH, C = GHFt , D = FHt Ft .
m
P
fik (gkj + hkj ) ;
Ответ. aij =
buv =
cxy =
m P
m
P
p=1 q=1
m P
m
P
k=1
fup gpq hqv ;
gxp hpq fyq ;
p=1 q=1
dxy =
PP
p=1 q=1
fxp h p fy .
Задача 3. Для матриц Fn×m , Gm×m и Hm×m запишите формулы для вычисления коэффициентов матриц A = F (G + H), B = FGH, C = GHFt , D = FHt Ft .
m
P
fik (gkj + hkj ) ;
Ответ. aij =
buv =
cxy =
m P
m
P
p=1 q=1
m P
m
P
k=1
fup gpq hqv ;
gxp hpq fyq ;
p=1 q=1
dxy =
PP
p=1 q=1
fxp hqp fyq .
Задача 3. Для матриц Fn×m , Gm×m и Hm×m запишите формулы для вычисления коэффициентов матриц A = F (G + H), B = FGH, C = GHFt , D = FHt Ft .
m
P
fik (gkj + hkj ) ;
Ответ. aij =
buv =
cxy =
dxy =
m P
m
P
p=1 q=1
m P
m
P
p=1 q=1
m P
P
p=1 q=1
k=1
fup gpq hqv ;
gxp hpq fyq ;
fxp hqp fyq .
Задача 3. Для матриц Fn×m , Gm×m и Hm×m запишите формулы для вычисления коэффициентов матриц A = F (G + H), B = FGH, C = GHFt , D = FHt Ft .
m
P
fik (gkj + hkj ) ;
Ответ. aij =
buv =
cxy =
dxy =
m P
m
P
p=1 q=1
m P
m
P
p=1 q=1
n
m P
P
p=1 q=1
k=1
fup gpq hqv ;
gxp hpq fyq ;
fxp hqp fyq .
Решение задачи 4.
2 5
−3 1

Задача 4. Найдите
произведения
матриц:




−2 0 1 −1
−1 2
2 −1 2
3 −1
0 
3 1   3 1  =?.
2 1 1
0  =?,  2
1
0 −1
−2 1
2 −1 1
1 0 0
1
3 1 0
1
−1 1 1 −1
=?,
2 5
−3 1

Найдите
произведения
матриц:




−2 0 1 −1
−1 2
2 −1 2
3 −1
0 




3 1  =?.
2
3 1
2 1 1
0
=?,
1
0 −1
−2 1
2 −1 1
1 0 0
1
2 5
3 1 0
1
1
7 5 −3
Ответ.
=
,
−3 1
−1 1 1 −1
−10 −2 1 −4
Задача 4.
3 1 0
1
−1 1 1 −1
=?,
Найдите

−2 0 1
3 −1
0 
2 1 1
1
0 −1
1 0 0
2 5
3
Ответ.
−3 1
−1

−2 0 1
3 −1
0 
2 1 1
1
0 −1
1 0 0
Задача 4.
произведения


2
−1


2
0
=?,
2
1
1 0
1
=
1 1 −1

−1
−8
0 =
−3
1
2 5
−3 1

матриц:

−1 2
−1 2


3 1  =?.
3 1
−2 1
−1 1
1
7 5 −3
,
−10 −2 1 −4
−1 2 −3
,
0 1 −2
3 1 0
1
−1 1 1 −1
=?,
Найдите
произведения



−2 0 1 −1
2
3 −1
0 


2
2 1 1
0
=?,
1
0 −1
2
1 0 0
1
2 5
3 1 0
1
Ответ.
=
−3 1
−1 1 1 −1


−2 0 1 −1
3 −1
0 
−8
2 1 1
0 =
1
0 −1
−3
1 0 0
1


 

2 −1 2
−1 2
−9 5
 2
3 1   3 1  =  5 8 .
2 −1 1
−2 1
−7 4
Задача 4.
2 5
−3 1

матриц:

−1 2
−1 2


3 1  =?.
3 1
−2 1
−1 1
1
7 5 −3
,
−10 −2 1 −4
−1 2 −3
,
0 1 −2
3 1 0
1
−1 1 1 −1
=?,
Решение задачи 5.

2 −1 2
Задача 5. Вычислить значение многочлена x2 − 2x − 4 при x =  1 −1 0 .
3 −1 1


2 −1 2
Задача 5. Вычислить значение многочлена x2 − 2x − 4 при x =  1 −1 0 .
3 −1 1

Ответ. x2 =

2 −1 2
Задача 5. Вычислить значение многочлена x2 − 2x − 4 при x =  1 −1 0 .
3 −1 1


9 −3 6
0 2 ,
Ответ. x2 =  1
8 −3 7


2 −1 2
Задача 5. Вычислить значение многочлена x2 − 2x − 4 при x =  1 −1 0 .
3 −1 1


9 −3 6
0 2 ,
Ответ. x2 =  1
8 −3 7

x2 − 2x =

2 −1 2
Задача 5. Вычислить значение многочлена x2 − 2x − 4 при x =  1 −1 0 .
3 −1 1


9 −3 6
0 2 ,
Ответ. x2 =  1
8 −3 7




9 −3 6
2 −1 2
0 2  − 2  1 −1 0  =
x2 − 2x =  1
8 −3 7
3 −1 1


2 −1 2
Задача 5. Вычислить значение многочлена x2 − 2x − 4 при x =  1 −1 0 .
3 −1 1


9 −3 6
0 2 ,
Ответ. x2 =  1
8 −3 7



 

9 −3 6
2 −1 2
5 −1 2
0 2  − 2  1 −1 0  =  −1
2 2 ,
x2 − 2x =  1
8 −3 7
3 −1 1
2 −1 5


2 −1 2
Задача 5. Вычислить значение многочлена x2 − 2x − 4 при x =  1 −1 0 .
3 −1 1


9 −3 6
0 2 ,
Ответ. x2 =  1
8 −3 7



 

9 −3 6
2 −1 2
5 −1 2
0 2  − 2  1 −1 0  =  −1
2 2 ,
x2 − 2x =  1
8 −3 7
3 −1 1
2 −1 5

x2 − 2x − 4E =

2 −1 2
Задача 5. Вычислить значение многочлена x2 − 2x − 4 при x =  1 −1 0 .
3 −1 1


9 −3 6
0 2 ,
Ответ. x2 =  1
8 −3 7



 

9 −3 6
2 −1 2
5 −1 2
0 2  − 2  1 −1 0  =  −1
2 2 ,
x2 − 2x =  1
8 −3 7
3 −1 1
2 −1 5




5 −1 2
1 0 0
2 2  − 4 0 1 0  =
x2 − 2x − 4E =  −1
2 −1 5
0 0 1


2 −1 2
Задача 5. Вычислить значение многочлена x2 − 2x − 4 при x =  1 −1 0 .
3 −1 1


9 −3 6
0 2 ,
Ответ. x2 =  1
8 −3 7



 

9 −3 6
2 −1 2
5 −1 2
0 2  − 2  1 −1 0  =  −1
2 2 ,
x2 − 2x =  1
8 −3 7
3 −1 1
2 −1 5



 

5 −1 2
1 0 0
1 −1 2
2 2  − 4  0 1 0  =  −1 −2 2 .
x2 − 2x − 4E =  −1
2 −1 5
0 0 1
2 −1 1

Решение задачи 6.
Задача 6. С помощью
матриц
«на макроуровне» подберите матрицы X и Y с


 умножения
1 −1
1 2 3
тем, чтобы X  4 5 6  Y =  4 −4 .
7 −7
7 8 9
Задача
матриц «на макроуровне» подберите матрицы X и Y с тем,


 умножения
6. С помощью
1 −1
1 2 3
чтобы X  4 5 6  Y =  4 −4 .
7 −7
7 8 9
Ответ. Заметим, что матрица в правой
 равенства получена дублированием и умно части этого
1 2 3
жением на константу столбцов матрицы  4 5 6 .
7 8 9
Задача
матриц «на макроуровне» подберите матрицы X и Y с тем,


 умножения
6. С помощью
1 −1
1 2 3
чтобы X  4 5 6  Y =  4 −4 .
7 −7
7 8 9
Ответ. Заметим, что матрица в правой
части этогоравенства получена дублированием и умно1 2 3

4 5 6 . Так как строки при этом не менялись, то
жением на константу столбцов матрицы
7 8 9


1 0 0

0 1 0 .
можно положить X =
0 0 1
Задача
матриц «на макроуровне» подберите матрицы X и Y с тем,


 умножения
6. С помощью
1 −1
1 2 3
чтобы X  4 5 6  Y =  4 −4 .
7 −7
7 8 9
Ответ. Заметим, что матрица в правой
части этогоравенства получена дублированием и умно1 2 3

4 5 6 . Так как строки при этом не менялись, то
жением на константу столбцов матрицы
7 8 9


1 0 0

0 1 0 .
можно положить X =
0 0 1
Используя «умножение на макроуровне», получаем Y = Y1 Y2 , где
Задача
матриц «на макроуровне» подберите матрицы X и Y с тем,


 умножения
6. С помощью
1 −1
1 2 3
чтобы X  4 5 6  Y =  4 −4 .
7 −7
7 8 9
Ответ. Y = Y1 Y2 , где
 
 
 
 
1
1
2
3
 4  =?  4  +?  5  +?  6  =
7
7
8
9
Задача
матриц «на макроуровне» подберите матрицы X и Y с тем,


 умножения
6. С помощью
1 −1
1 2 3
чтобы X  4 5 6  Y =  4 −4 .
7 −7
7 8 9
Ответ. Y = Y1 Y2 , где
 
 
 
 
1
1
2
3
 4  = 1 4  + 0 5  + 0 6  =
7
7
8
9
Задача
матриц «на макроуровне» подберите матрицы X и Y с тем,


 умножения
6. С помощью
1 −1
1 2 3
чтобы X  4 5 6  Y =  4 −4 .
7 −7
7 8 9
Ответ. Y = Y1 Y2 , где
 
 
 
  
 
1
1
2
3
1 2 3
1
 4  = 1 4  + 0 5  + 0 6  =  4 5 6  0  ⇒
7
7
8
9
7 8 9
0
Задача
матриц «на макроуровне» подберите матрицы X и Y с тем,


 умножения
6. С помощью
1 −1
1 2 3
чтобы X  4 5 6  Y =  4 −4 .
7 −7
7 8 9
Ответ. Y = Y1 Y2 , где
 
 
 
  
 
1
1
2
3
1 2 3
1
 4  = 1 4  + 0 5  + 0 6  =  4 5 6  0  ⇒
7
7
8
9
7 8 9
0
 
1

0 ,
⇒ Y1 =
0
Задача
матриц «на макроуровне» подберите матрицы X и Y с тем,


 умножения
6. С помощью
1 −1
1 2 3
чтобы X  4 5 6  Y =  4 −4 .
7 −7
7 8 9
Ответ. Y = Y1 Y2 , где


 
 
 
−1
1
2
3
 −4  = −1  4  + 0  5  + 0  6  =
−7
7
8
9
Задача
матриц «на макроуровне» подберите матрицы X и Y с тем,


 умножения
6. С помощью
1 −1
1 2 3
чтобы X  4 5 6  Y =  4 −4 .
7 −7
7 8 9
Ответ. Y = Y1 Y2 , где


 
 
  


−1
1
2
3
1 2 3
−1
 −4  = −1  4  + 0  5  + 0  6  =  4 5 6   0  ⇒
−7
7
8
9
7 8 9
0
Задача
матриц «на макроуровне» подберите матрицы X и Y с тем,


 умножения
6. С помощью
1 −1
1 2 3
чтобы X  4 5 6  Y =  4 −4 .
7 −7
7 8 9
Ответ. Y = Y1 Y2 , где


 
 
  


−1
1
2
3
1 2 3
−1
 −4  = −1  4  + 0  5  + 0  6  =  4 5 6   0  ⇒
−7
7
8
9
7 8 9
0


−1
⇒ Y2 =  0  .
0
Задача
матриц «на макроуровне» подберите матрицы X и Y с тем,


 умножения
6. С помощью
1 −1
1 2 3
чтобы X  4 5 6  Y =  4 −4 .
7 −7
7 8 9


1 −1
0 . Таким образом,
Ответ. Значит, Y =  0
0
0

 



1 −1
1 0 0
1 2 3
1 −1
 4 −4  =  0 1 0   4 5 6   0
0 .
7 −7
0 0 1
7 8 9
0
0
Решение задачи 7.
Задача 7. С помощью
 умножения матриц «на макроуровне» подберите матрицы X и Y с
1 2 3
4
−4
.
тем, чтобы X  4 5 6  Y =
7 −7
7 8 9
Задача
 умножения матриц «на макроуровне» подберите матрицы X и Y с тем,
7. С помощью
1 2 3
4 −4


4 5 6 Y =
.
чтобы X
7 −7
7 8 9
Ответ. Отличие от предыдущего примера состоит в том, что нам надо еще убрать первую строчку
в матрице

 


1 −1
1 2 3
1 −1
 4 −4  =  4 5 6   0
0 .
7 −7
7 8 9
0
0
0 1 0
Для этого достаточно обе части этого равенства умножить слева на
. В итоге получим
0 0 1
Задача
 умножения матриц «на макроуровне» подберите матрицы X и Y с тем,
7. С помощью
1 2 3
4 −4


4 5 6 Y =
.
чтобы X
7 −7
7 8 9
Ответ.



1 2 3
1 −1
4 −4
0 1 0 
0 ,
4 5 6  0
=
7 −7
0 0 1
0
0
7 8 9


1 −1
0 1 0

0
0 .
то есть X =
, Y =
0 0 1
0
0
Решение задачи 8.
Задача 8. С помощьюумножения матриц
«на макроуровне»
сведите решение трех си
x − y = 1,
a − b = 2,
α − β = 0,
стем линейных уравнений:
к одному матричному
x + y = −1,
a + b = 2,
α + β = 2,
уравнению.
Задача 8. С помощью
умножения матриц «на макроуровне»
сведите решение трех систем ли
x − y = 1,
a − b = 2,
α − β = 0,
нейных уравнений:
к одному матричному уравx + y = −1,
a + b = 2,
α + β = 2,
нению.
Ответ. Сначала запишем каждую систему в матричном виде:
Задача 8. С помощью
умножения матриц «на макроуровне»
сведите решение трех систем ли
x − y = 1,
a − b = 2,
α − β = 0,
нейных уравнений:
к одному матричному уравx + y = −1,
a + b = 2,
α + β = 2,
нению.
Ответ. Сначала запишем каждую систему в матричном виде:
1 −1
x
1
=
,
1
1
y
−1
Задача 8. С помощью
умножения матриц «на макроуровне»
сведите решение трех систем ли
x − y = 1,
a − b = 2,
α − β = 0,
нейных уравнений:
к одному матричному уравx + y = −1,
a + b = 2,
α + β = 2,
нению.
Ответ. Сначала запишем каждую систему в матричном виде:
1 −1
x
1
=
,
1
1
y
−1
1 −1
a
2
=
,
1
1
b
2
Задача 8. С помощью
умножения матриц «на макроуровне»
сведите решение трех систем ли
x − y = 1,
a − b = 2,
α − β = 0,
нейных уравнений:
к одному матричному уравx + y = −1,
a + b = 2,
α + β = 2,
нению.
Ответ. Сначала запишем каждую систему в матричном виде:
1 −1
x
1
=
,
1
1
y
−1
1 −1
a
2
1 −1
α
0
=
,
=
.
1
1
b
2
1
1
β
2
Задача 8. С помощью
умножения матриц «на макроуровне»
сведите решение трех систем ли
x − y = 1,
a − b = 2,
α − β = 0,
нейных уравнений:
к одному матричному уравx + y = −1,
a + b = 2,
α + β = 2,
нению.
Ответ. Сначала запишем каждую систему в матричном виде:
1 −1
x
1
=
,
1
1
y
−1
1 −1
a
2
1 −1
α
0
=
,
=
.
1
1
b
2
1
1
β
2
С
эти три уравнения «сшиваются» в одно
помощью
«умножения
на макроуровне»
1 −1
x a α
1 2 0
=
.
1
1
y b β
−1 2 2
Задача 8. С помощью
умножения матриц «на макроуровне»
сведите решение трех систем ли
x − y = 1,
a − b = 2,
α − β = 0,
нейных уравнений:
к одному матричному уравx + y = −1,
a + b = 2,
α + β = 2,
нению.
1 −1
x a α
1 2 0
Ответ. Кстати, матричное уравнение
=
легко решается
1
1
y b β
−1 2 2
с помощью «умножения на макроуровне».
Задача 8. С помощью
умножения матриц «на макроуровне»
сведите решение трех систем ли
x − y = 1,
a − b = 2,
α − β = 0,
нейных уравнений:
к одному матричному уравx + y = −1,
a + b = 2,
α + β = 2,
нению.
1 2 0
1
−1
Ответ. В самом деле, первый столбец матрицы
— это 0 ·
+ (−1) ·
,
−1 2 2
1
1
аналогично «в уме» подбираются коэффициенты
столбцав линей
в разложении
второго итретьего
1 −1
x a α
0 2 1
. Получаем
=
, то есть
ную комбинацию столбцов матрицы
1
1
y b β
−1 0 1
x = 0,
a = 2,
α = 1,
y = −1,
b = 0,
β = 1.
Решение задачи 9.
Задача 9. Функцию, вычисляющую сумму всех элементов матрицы размерности 3 × 2, определить формулой, использующей только умножение матриц и детерминант.
Задача 9. Функцию, вычисляющую сумму всех элементов матрицы размерности 3 × 2, определить формулой, использующей
только умножение
матриц и детерминант.
1
1 1 1 ·X ·
Ответ. f (X) = det
.
1
Решение
задачи
10.

Задача 10. Следует ли из равенства
1 −1 2
1
0 1

1 −1 2
1
0 1


−2
3
и  1 −1  — обратные друг к другу?
2 −2
−2
3
1 0

1 −1
, что матрицы
=
0 1
2 −2
Задача 10. Следует ли из равенства
1 −1 2
1
0 1

−2
3
1
0
 1 −1  =
, что матрицы
0 1
2 −2


−2
3
1 −1 2
и  1 −1  — обратные друг к другу?
1
0 1
2 −2
Ответ. Нет, не следует, так как эти матрицы не квадратные.

Решение задачи 11.
Задача 11. Как из матрицы A−1 размерности 3 × 3 получить матрицу B −1 , если B получена из
A перестановкой первой и третьей строк?
Задача 11. Как из матрицы A−1 размерности 3 × 3 получить матрицу B −1 , если B получена из A
перестановкой первой и третьей строк?
Ответ. Для того, чтобы получить матрицу B −1 , надо в матрице A−1 переставить местами первый итретий столбцы.
В самом деле, с помощью «умножения матриц на макроуровне», получаем

0 0 1
B =  0 1 0  A, поэтому, согласно свойствам обратной матрицы,
1 0 0
Задача 11. Как из матрицы A−1 размерности 3 × 3 получить матрицу B −1 , если B получена из A
перестановкой первой и третьей строк?
Ответ. Для того, чтобы получить матрицу B −1 , надо в матрице A−1 переставить местами первый итретий столбцы.
В самом деле, с помощью «умножения матриц на макроуровне», получаем

0 0 1
B =  0 1 0  A, поэтому, согласно свойствам обратной матрицы,
1 0 0
 −1
0 0 1
=  0 1 0  A  =
1 0 0

B −1
Задача 11. Как из матрицы A−1 размерности 3 × 3 получить матрицу B −1 , если B получена из A
перестановкой первой и третьей строк?
Ответ. Для того, чтобы получить матрицу B −1 , надо в матрице A−1 переставить местами первый итретий столбцы.
В самом деле, с помощью «умножения матриц на макроуровне», получаем

0 0 1
B =  0 1 0  A, поэтому, согласно свойствам обратной матрицы,
1 0 0
 −1

−1
0 0 1
0 0 1
=  0 1 0  A = A−1  0 1 0  =
1 0 0
1 0 0

B −1
Задача 11. Как из матрицы A−1 размерности 3 × 3 получить матрицу B −1 , если B получена из A
перестановкой первой и третьей строк?
Ответ. Для того, чтобы получить матрицу B −1 , надо в матрице A−1 переставить местами первый итретий столбцы.
В самом деле, с помощью «умножения матриц на макроуровне», получаем

0 0 1
B =  0 1 0  A, поэтому, согласно свойствам обратной матрицы,
1 0 0
 −1

−1


0 0 1
0 0 1
0 0 1
=  0 1 0  A = A−1  0 1 0  = A−1  0 1 0  .
1 0 0
1 0 0
1 0 0

B −1
Задача 11. Как из матрицы A−1 размерности 3 × 3 получить матрицу B −1 , если B получена из A
перестановкой первой и третьей строк?
Ответ. Как следует из результатов раздела,
посвященного
умножению на макроуровне, умно

0 0 1
жение матрицы A−1 справа на матрицу  0 1 0  осуществляет перестановку первого и третье1 0 0
−1
го столбцов матрицы A .
Решение задачи 12.
Задача 12. Найдите матрицу, обратную к матрице A =
1
2
−3 −4
.
1
2
Задача 12. Найдите матрицу, обратную к матрице A =
.
−3 −4
Ответ. Обычно применяется один из двух методов вычисления обратной матрицы.
1
2
Задача 12. Найдите матрицу, обратную к матрице A =
.
−3 −4
Ответ. Проверить ваши результаты вычисления обратной матрицы с помощью присоединенной матрицы?
Проверить ваши результаты вычисления обратной матрицы с помощью метода Гаусса?
1
2
Задача 12. Найдите матрицу, обратную к матрице A =
.
−3 −4
Ответ. Вычислим обратную матрицу с помощью присоединенной матрицы.
1
2
Задача 12. Найдите матрицу, обратную к матрице A =
.
−3 −4
Ответ. Вычислим обратную матрицу с помощью присоединенной матрицы.
Сначала
миноров элементов:
составим
матрицу
из дополнительных
1
2
A=
,
−3 −4
1
2
Задача 12. Найдите матрицу, обратную к матрице A =
.
−3 −4
Ответ. Вычислим обратную матрицу с помощью присоединенной матрицы.
Сначала
миноров элементов:
составим
матрицу
из дополнительных
1
2
−4
A=
,
−3 −4
1
2
Задача 12. Найдите матрицу, обратную к матрице A =
.
−3 −4
Ответ. Вычислим обратную матрицу с помощью присоединенной матрицы.
Сначала
миноров элементов:
составим
матрицу
из дополнительных
1
2
−4 −3
A=
,
−3 −4
1
2
Задача 12. Найдите матрицу, обратную к матрице A =
.
−3 −4
Ответ. Вычислим обратную матрицу с помощью присоединенной матрицы.
Сначала
миноров элементов:
составим
матрицу
из дополнительных
1
2
−4 −3
A=
,
−3 −4
2
1
2
Задача 12. Найдите матрицу, обратную к матрице A =
.
−3 −4
Ответ. Вычислим обратную матрицу с помощью присоединенной матрицы.
Сначала
миноров элементов:
составим
матрицу
из дополнительных
1
2
−4 −3
A=
,
−3 −4
2
1
1
2
Задача 12. Найдите матрицу, обратную к матрице A =
.
−3 −4
Ответ. Вычислим обратную матрицу с помощью присоединенной матрицы.
Сменим
местах,
алгебраические дополнения.
знаки в соответствующих
чтобы получить
1
2
−4 −3
A=
,
,
−3 −4
2
1
1
2
Задача 12. Найдите матрицу, обратную к матрице A =
.
−3 −4
Ответ. Вычислим обратную матрицу с помощью присоединенной матрицы.
Сменим
местах,
алгебраические дополнения.
знаки в соответствующих
чтобы получить
1
2
−4 −3
−4
A=
,
,
−3 −4
2
1
1
1
2
Задача 12. Найдите матрицу, обратную к матрице A =
.
−3 −4
Ответ. Вычислим обратную матрицу с помощью присоединенной матрицы.
Сменим
местах,
алгебраические дополнения.
знаки в соответствующих
чтобы получить
1
2
−4 −3
−4 3
A=
,
,
−3 −4
2
1
−2 1
1
2
Задача 12. Найдите матрицу, обратную к матрице A =
.
−3 −4
Ответ. Вычислим обратную матрицу с помощью присоединенной матрицы.
Транспонируем
последнюю
матрицу.
матрицу,
чтобы
получить
присоединенную
1
2
−4 −3
−4 3
A=
,
,
,
PA =
−3 −4
2
1
−2 1
1
2
Задача 12. Найдите матрицу, обратную к матрице A =
.
−3 −4
Ответ. Вычислим обратную матрицу с помощью присоединенной матрицы.
Транспонируем
последнюю
матрицу.
матрицу,
чтобы
получить
присоединенную
1
2
−4 −3
−4 3
−4 −2
A=
,
,
,
PA =
−3 −4
2
1
−2 1
1
2
Задача 12. Найдите матрицу, обратную к матрице A =
.
−3 −4
Ответ. Вычислим обратную матрицу с помощью присоединенной матрицы.
Транспонируем
последнюю
матрицу.
матрицу,
чтобы
получить
присоединенную
1
2
−4 −3
−4 3
−4 −2
A=
,
,
,
PA =
−3 −4
2
1
−2 1
3
1
1
2
Задача 12. Найдите матрицу, обратную к матрице A =
.
−3 −4
Ответ. Вычислим обратную матрицу с помощью присоединенной матрицы.
Транспонируем
последнюю
матрицу.
матрицу,
чтобы
получить
присоединенную
1
2
−4 −3
−4 3
−4 −2
A=
,
,
,
PA =
−3 −4
2
1
−2 1
3
1
Осталось найти детерминант исходной матрицы. Элементами присоединенной матрицы являются
алгебраические дополнения к элементам матрицы, поэтому по теореме о разложении детерминанта по строке или столбцу имеем:
1
2
Задача 12. Найдите матрицу, обратную к матрице A =
.
−3 −4
Ответ. Вычислим обратную матрицу с помощью присоединенной матрицы.
Транспонируем
последнюю
матрицу.
матрицу,
чтобы
получить
присоединенную
1
2
−4 −3
−4 3
−4 −2
A=
,
,
,
PA =
−3 −4
2
1
−2 1
3
1
Осталось найти детерминант исходной матрицы. Элементами присоединенной матрицы являются
алгебраические дополнения к элементам матрицы, поэтому по теореме о разложении детерминанта по строке или столбцу имеем:
det A = 1 · (−4) + 2 · 3 =
1
2
Задача 12. Найдите матрицу, обратную к матрице A =
.
−3 −4
Ответ. Вычислим обратную матрицу с помощью присоединенной матрицы.
Транспонируем
последнюю
матрицу.
матрицу,
чтобы
получить
присоединенную
1
2
−4 −3
−4 3
−4 −2
A=
,
,
,
PA =
−3 −4
2
1
−2 1
3
1
Осталось найти детерминант исходной матрицы. Элементами присоединенной матрицы являются
алгебраические дополнения к элементам матрицы, поэтому по теореме о разложении детерминанта по строке или столбцу имеем:
det A = 1 · (−4) + 2 · 3 = 2,
1
2
Задача 12. Найдите матрицу, обратную к матрице A =
.
−3 −4
Ответ. Вычислим обратную матрицу с помощью присоединенной матрицы.
Транспонируем
последнюю
матрицу.
матрицу,
чтобы
получить
присоединенную
1
2
−4 −3
−4 3
−4 −2
A=
,
,
,
PA =
−3 −4
2
1
−2 1
3
1
Осталось найти детерминант исходной матрицы. Элементами присоединенной матрицы являются
алгебраические дополнения к элементам матрицы, поэтому по теореме о разложении детерминанта по строке или столбцу имеем:
det A = 1 · (−4) + 2 · 3 = 2,
det A = (−3) · (−2) + (−4) · 1 =
1
2
Задача 12. Найдите матрицу, обратную к матрице A =
.
−3 −4
Ответ. Вычислим обратную матрицу с помощью присоединенной матрицы.
Транспонируем
последнюю
матрицу.
матрицу,
чтобы
получить
присоединенную
1
2
−4 −3
−4 3
−4 −2
A=
,
,
,
PA =
−3 −4
2
1
−2 1
3
1
Осталось найти детерминант исходной матрицы. Элементами присоединенной матрицы являются
алгебраические дополнения к элементам матрицы, поэтому по теореме о разложении детерминанта по строке или столбцу имеем:
det A = 1 · (−4) + 2 · 3 = 2,
det A = (−3) · (−2) + (−4) · 1 = 2.
1
2
Задача 12. Найдите матрицу, обратную к матрице A =
.
−3 −4
Ответ. Вычислим обратную матрицу с помощью присоединенной матрицы.
Транспонируем
последнюю
матрицу.
матрицу,
чтобы
получить
присоединенную
1
2
−4 −3
−4 3
−4 −2
A=
,
,
,
PA =
−3 −4
2
1
−2 1
3
1
Осталось найти детерминант исходной матрицы. Элементами присоединенной матрицы являются
алгебраические дополнения к элементам матрицы, поэтому по теореме о разложении детерминанта по строке или столбцу имеем:
det A = 1 · (−4) + 2 · 3 = 2,
det A = (−3) · (−2) + (−4) · 1 = 2.
Значит, из доказательства
теоремы об условии обратимости квадратной матрицы
1
−4 −2
A−1 =
.
3
1
2
1
2
Задача 12. Найдите матрицу, обратную к матрице A =
.
−3 −4
Ответ. Вычислим обратную матрицу с помощью присоединенной матрицы.
Транспонируем
последнюю
матрицу.
матрицу,
чтобы
получить
присоединенную
1
2
−4 −3
−4 3
−4 −2
A=
,
,
,
PA =
−3 −4
2
1
−2 1
3
1
Осталось найти детерминант исходной матрицы. Элементами присоединенной матрицы являются
алгебраические дополнения к элементам матрицы, поэтому по теореме о разложении детерминанта по строке или столбцу имеем:
det A = 1 · (−4) + 2 · 3 = 2,
det A = (−3) · (−2) + (−4) · 1 = 2.
Значит, из доказательства
теоремы об условии обратимости квадратной матрицы
1
−4 −2
A−1 =
.
3
1
2
Проверить ваши результаты вычисления обратной матрицы с помощью метода Гаусса?
1
2
Задача 12. Найдите матрицу, обратную к матрице A =
−3 −4
Ответ. Вычислим обратную матрицу с помощью метода Гаусса.
.
1
2
Задача 12. Найдите матрицу, обратную к матрице A =
−3 −4
Ответ. Вычислим обратную матрицу с помощью метода Гаусса.
1
2 1 0
∼
−3 −4 0 1
.
1
2
Задача 12. Найдите матрицу, обратную к матрице A =
−3 −4
Ответ. Вычислим обратную матрицу с помощью метода Гаусса.
1
2 1 0
1 2 1 0
∼
∼
−3 −4 0 1
0 2 3 1
.
1
2
Задача 12. Найдите матрицу, обратную к матрице A =
−3 −4
Ответ. Вычислим обратную матрицу с помощью метода Гаусса.
1
2 1 0
1 2 1 0
1 2
1
0
∼
∼
∼
−3 −4 0 1
0 2 3 1
0 1 3/2 1/2
.
1
2
Задача 12. Найдите матрицу, обратную к матрице A =
.
−3 −4
Ответ. Вычислим обратную матрицу с помощью метода Гаусса.
1
2 1 0
1 2 1 0
1 2
1 0 −2 −1
1
0
∼
∼
∼
−3 −4 0 1
0 2 3 1
0 1 3/2 1/2
0 1 3/2 1/2
1
2
Задача 12. Найдите матрицу, обратную к матрице A =
.
−3 −4
Ответ. Вычислим обратную матрицу с помощью метода Гаусса.
1
2 1 0
1 2 1 0
1 2
1 0 −2 −1
1
0
∼
∼
∼
−3 −4 0 1
0 2 3 1
0 1 3/2 1/2
0 1 3/2 1/2
−2 −1
−1
Значит, A =
.
3/2 1/2
1
2
Задача 12. Найдите матрицу, обратную к матрице A =
.
−3 −4
Ответ. Вычислим обратную матрицу с помощью метода Гаусса.
1
2 1 0
1 2 1 0
1 2
1
0
1 0 −2 −1
∼
∼
∼
−3 −4 0 1
0 2 3 1
0 1 3/2 1/2
0 1 3/2 1/2
−2 −1
.
Значит, A−1 =
3/2 1/2
Проверить ваши результаты вычисления обратной матрицы с помощью присоединенной матрицы?
1
2
Задача 12. Найдите матрицу, обратную к матрице A =
−3 −4
1 −4 −2
−2 −1
−1
Ответ. Итак, получили A =
=
.
3
1
3/2 1/2
2
.
Решение задачи 13.
Задача 13. Вычислите

−1 2 −3
B =  −1 2 −1 ,
−2 5 −1

матрицы,

−8
28
 −12
32
C=
 −20
40
16 −36
обратную

−9 −15
−1 −15 
.
−5 −15 
8
20
к
матрицам
A=
0 −5
2 25
,
Задача 13.
Вычислите
матрицы,


−8
28
−1 2 −3
 −12
32
B =  −1 2 −1 , C = 
 −20
40
−2 5 −1
16 −36
2.5 0.5
Ответ. A−1 =
,
−0.2
0

обратную

−9 −15
−1 −15 
.
−5 −15 
8
20
к
матрицам
A=
0 −5
2 25
,
Задача 13.
Вычислите
матрицы,


−8
28
−1 2 −3
 −12
32
B =  −1 2 −1 , C = 
 −20
40
−2 5 −1
16 −36
2.5 0.5
Ответ. A−1 =
,
−0.2
0


1.5 −6.5 2
−1

0.5 −2.5 1 ,
B =
−0.5
0.5 0

обратную

−9 −15
−1 −15 
.
−5 −15 
8
20
к
матрицам
A=
0 −5
2 25
,
Задача 13.
Вычислите
матрицы,


−8
28
−1 2 −3
 −12
32
B =  −1 2 −1 , C = 
 −20
40
−2 5 −1
16 −36
2.5 0.5
Ответ. A−1 =
,
−0.2
0


1.5 −6.5 2
−1

0.5 −2.5 1 ,
B =
−0.5
0.5 0


3
2 −1 3
 2
1
1 3 

C−1 = 
 −2
3 −1 0 
2 −1
3 4

обратную

−9 −15
−1 −15 
.
−5 −15 
8
20
к
матрицам
A=
0 −5
2 25
,
Решение задачи 14.
Задача 14. Решите
2 −1
1 −1
Y
=
−3
1
2 −2
2
3
1 −2
T =
−3 −4
3
4
2 −1
матричные
уравнения:
−3
1
2 −1
3 −2
−13 −6
,
Z
=
,
−3
1
4
1
18 10
5
.
−1
X=
1 −1
2 −2
,
2 −1
1 −1
Задача 14.
Решите
матричные
уравнения:
X=
,
−3
1
2 −2
2 −1
1 −1
2 −1
3 −2
−13 −6
Y
=
,
Z
=
,
−3
1
2 −2
−3
1
4
1
18 10
2
3
1 −2
5
T =
.
−3 −4
3
4 −1
2 −1
1 −1
Ответ. Уравнение
X=
можно решить методом Гаусса или с помо−3
1
2 −2
щью обратной матрицы.
2 −1
1 −1
Задача 14.
Решите
матричные
уравнения:
X=
,
−3
1
2 −2
2 −1
1 −1
2 −1
3 −2
−13 −6
Y
=
,
Z
=
,
−3
1
2 −2
−3
1
4
1
18 10
2
3
1 −2
5
T =
.
−3 −4
3
4 −1
2 −1
1 −1
Ответ. Уравнение
X=
можно решить методом Гаусса или с помощью
−3
1
2 −2
обратной матрицы.
Проверить ваше решение методом Гаусса?
Проверить ваше решение с помощью обратной матрицы?
2 −1
1 −1
Задача 14.
Решите
матричные
уравнения:
X=
,
−3
1
2 −2
2 −1
1 −1
2 −1
3 −2
−13 −6
Y
=
,
Z
=
,
−3
1
2 −2
−3
1
4
1
18 10
2
3
1 −2
5
T =
.
−3 −4
3
4 −1
2 −1
1 −1
Ответ. Решение уравнения
X=
методом Гаусса.
−3
1
2 −2
2 −1
1 −1
Задача 14.
Решите
матричные
уравнения:
X=
,
−3
1
2 −2
2 −1
1 −1
2 −1
3 −2
−13 −6
Y
=
,
Z
=
,
−3
1
2 −2
−3
1
4
1
18 10
2
3
1 −2
5
T =
.
−3 −4
3
4 −1
2 −1
1 −1
Ответ. Решение уравнения
X=
методом Гаусса.
−3
1
2 −2
1
2 −1 1 −1
=
1
−3
1 2 −2
2 −1
1 −1
Задача 14.
Решите
матричные
уравнения:
X=
,
−3
1
2 −2
2 −1
1 −1
2 −1
3 −2
−13 −6
Y
=
,
Z
=
,
−3
1
2 −2
−3
1
4
1
18 10
2
3
1 −2
5
T =
.
−3 −4
3
4 −1
2 −1
1 −1
Ответ. Решение уравнения
X=
методом Гаусса.
−3
1
2 −2
1 1
2 −1 1 −1
=
0 1
−3
1 2 −2
2 −1
1 −1
Задача 14.
Решите
матричные
уравнения:
X=
,
−3
1
2 −2
2 −1
1 −1
2 −1
3 −2
−13 −6
Y
=
,
Z
=
,
−3
1
2 −2
−3
1
4
1
18 10
2
3
1 −2
5
T =
.
−3 −4
3
4 −1
2 −1
1 −1
Ответ. Решение уравнения
X=
методом Гаусса.
−3
1
2 −2
1 1
2 −1 1 −1
−1 0 3 −3
=
,
0 1
−3
1 2 −2
−3 1 2 −2
2 −1
1 −1
Задача 14.
Решите
матричные
уравнения:
X=
,
−3
1
2 −2
2 −1
1 −1
2 −1
3 −2
−13 −6
Y
=
,
Z
=
,
−3
1
2 −2
−3
1
4
1
18 10
2
3
1 −2
5
T =
.
−3 −4
3
4 −1
2 −1
1 −1
Ответ. Решение уравнения
X=
методом Гаусса.
−3
1
2 −2
1 1
2 −1 1 −1
−1 0 3 −3
=
,
0 1
−3
1 2 −2
−3 1 2 −2
−1 0
−1 0 3 −3
1 0 −3 3
=
.
−3 1 2 −2
0 1 −7 7
−3 1
2 −1
1 −1
Задача 14.
Решите
матричные
уравнения:
X=
,
−3
1
2 −2
2 −1
1 −1
2 −1
3 −2
−13 −6
Y
=
,
Z
=
,
−3
1
2 −2
−3
1
4
1
18 10
2
3
1 −2
5
T =
.
−3 −4
3
4 −1
2 −1
1 −1
Ответ. Решение уравнения
X=
методом Гаусса.
−3
1
2 −2
1 1
2 −1 1 −1
−1 0 3 −3
=
,
0 1
−3
1 2 −2
−3 1 2 −2
−1 0
−1 0 3 −3
1 0 −3 3
=
.
−3 1 2 −2
0 1 −7 7
−3 1
3 −3
Следовательно, X =
.
−7 −7
Проверить ваше решение с помощью обратной матрицы?
2 −1
1 −1
Задача 14.
Решите
матричные
уравнения:
X=
,
−3
1
2 −2
2 −1
1 −1
2 −1
3 −2
−13 −6
Y
=
,
Z
=
,
−3
1
2 −2
−3
1
4
1
18 10
2
3
1 −2
5
T =
.
−3 −4
3
4 −1
2 −1
1 −1
Ответ. Решение уравнения
X=
с помощью обратной матрицы.
−3
1
2 −2
2 −1
−3
1
X=
1 −1
2 −2
2 −1
1 −1
Задача 14.
Решите
матричные
уравнения:
X=
,
−3
1
2 −2
2 −1
1 −1
2 −1
3 −2
−13 −6
Y
=
,
Z
=
,
−3
1
2 −2
−3
1
4
1
18 10
2
3
1 −2
5
T =
.
−3 −4
3
4 −1
2 −1
1 −1
Ответ. Решение уравнения
X=
с помощью обратной матрицы.
−3
1
2 −2
2 −1
−3
1
−1 2 −1
−3
1
X=
2 −1
−3
1
−1 1 −1
2 −2
2 −1
1 −1
Задача 14.
Решите
матричные
уравнения:
X=
,
−3
1
2 −2
2 −1
1 −1
2 −1
3 −2
−13 −6
Y
=
,
Z
=
,
−3
1
2 −2
−3
1
4
1
18 10
2
3
1 −2
5
T =
.
−3 −4
3
4 −1
2 −1
1 −1
Ответ. Решение уравнения
X=
с помощью обратной матрицы.
−3
1
2 −2
X=
2 −1
−3
1
2 −1
−3
1
−1 −1 2 −1
−3
1
1 −1
2 −2
⇒
X=
2 −1
−3
1
−1 1 −1
2 −2
2 −1
1 −1
Задача 14.
Решите
матричные
уравнения:
X=
,
−3
1
2 −2
2 −1
1 −1
2 −1
3 −2
−13 −6
Y
=
,
Z
=
,
−3
1
2 −2
−3
1
4
1
18 10
2
3
1 −2
5
T =
.
−3 −4
3
4 −1
2 −1
1 −1
Ответ. Решение уравнения
X=
с помощью обратной матрицы.
−3
1
2 −2
X=
2 −1
−3
1
2 −1
−3
1
−1 −1 2 −1
−3
1
1 −1
2 −2
X=
⇒ X=
Проверить ваше решение методом Гаусса?
2 −1
−3
1
−1 −1
−3 −2
−1 1 −1
2 −2
1 −1
2 −2
=
−3 3
−7 7
.
2 −1
1 −1
Задача 14.
Решите
матричные
уравнения:
X=
,
−3
1
2 −2
2 −1
1 −1
2 −1
3 −2
−13 −6
Y
=
,
Z
=
,
−3
1
2 −2
−3
1
4
1
18 10
2
3
1 −2
5
T =
.
−3 −4
3
4 −1
2 −1
1 −1
Ответ. Y
=
Обычно применяется два варианта решения: применение
−3
1
2 −2
обратной матрицы или сведение к методу Гаусса (используя свойства транспонирования
матриц):
2 −1
1 −1
Задача 14.
Решите
матричные
уравнения:
X=
,
−3
1
2 −2
2 −1
1 −1
2 −1
3 −2
−13 −6
Y
=
,
Z
=
,
−3
1
2 −2
−3
1
4
1
18 10
2
3
1 −2
5
T =
.
−3 −4
3
4 −1
2 −1
1 −1
Ответ. Y
=
Обычно применяется два варианта решения: применение
−3
1
2 −2
обратной матрицы или сведение к методу Гаусса (используя свойства транспонирования
матриц):
t
t
2 −1
1 −1
t
Y =
−3
1
2 −2
2 −1
1 −1
Задача 14.
Решите
матричные
уравнения:
X=
,
−3
1
2 −2
2 −1
1 −1
2 −1
3 −2
−13 −6
Y
=
,
Z
=
,
−3
1
2 −2
−3
1
4
1
18 10
2
3
1 −2
5
T =
.
−3 −4
3
4 −1
2 −1
1 −1
Ответ. Y
=
Обычно применяется два варианта решения: применение
−3
1
2 −2
обратной матрицы или сведение к методу Гаусса (используя свойства транспонирования
матриц):
t
t
2 −1
1 −1
2 −3
1
2
t
∼
Y =
−3
1
2 −2
−1
1 −1 −2
2 −1
1 −1
Задача 14.
Решите
матричные
уравнения:
X=
,
−3
1
2 −2
2 −1
1 −1
2 −1
3 −2
−13 −6
Y
=
,
Z
=
,
−3
1
2 −2
−3
1
4
1
18 10
2
3
1 −2
5
T =
.
−3 −4
3
4 −1
2 −1
1 −1
Ответ. Y
=
Обычно применяется два варианта решения: применение
−3
1
2 −2
обратной матрицы или сведение к методу Гаусса (используя свойства транспонирования
матриц):
t
t
2 −1
1 −1
2 −3
1 0 2 4
1
2
t
∼
Y =
−3
1
2 −2
−1
1 −1 −2
0 1 1 2
2 −1
1 −1
Задача 14.
Решите
матричные
уравнения:
X=
,
−3
1
2 −2
2 −1
1 −1
2 −1
3 −2
−13 −6
Y
=
,
Z
=
,
−3
1
2 −2
−3
1
4
1
18 10
2
3
1 −2
5
T =
.
−3 −4
3
4 −1
2 −1
1 −1
Ответ. Y
=
Обычно применяется два варианта решения: применение
−3
1
2 −2
обратной матрицы или сведение к методу Гаусса (используя свойства транспонирования
матриц):
t
t
2 −1
1 −1
2 −3
1 0 2 4
1
2
t
∼
Y =
−3
1
2 −2
−1
1 −1 −2
0 1 1 2
2 4
t
Y =
⇒
1 2
2 −1
1 −1
Задача 14.
Решите
матричные
уравнения:
X=
,
−3
1
2 −2
2 −1
1 −1
2 −1
3 −2
−13 −6
Y
=
,
Z
=
,
−3
1
2 −2
−3
1
4
1
18 10
2
3
1 −2
5
T =
.
−3 −4
3
4 −1
2 −1
1 −1
Ответ. Y
=
Обычно применяется два варианта решения: применение
−3
1
2 −2
обратной матрицы или сведение к методу Гаусса (используя свойства транспонирования
матриц):
t
t
2 −1
1 −1
2 −3
1 0 2 4
1
2
t
∼
Y =
−3
1
2 −2
−1
1 −1 −2
0 1 1 2
2 4
2 1
t
Y =
⇒ Y =
.
1 2
4 2
2 −1
1 −1
Задача 14.
Решите
матричные
уравнения:
X=
,
−3
1
2 −2
2 −1
1 −1
2 −1
3 −2
−13 −6
Y
=
,
Z
=
,
−3
1
2 −2
−3
1
4
1
18 10
2
3
1 −2
5
T =
.
−3 −4
3
4 −1
2 −1
1 −1
Ответ. Y
=
Обычно применяется два варианта решения: применение
−3
1
2 −2
обратной матрицы или сведение к методу Гаусса (используя свойства транспонирования
матриц):
t
t
2 −1
1 −1
2 −3
1 0 2 4
1
2
t
∼
Y =
−3
1
2 −2
−1
1 −1 −2
0 1 1 2
2 4
2 1
t
Y =
⇒ Y =
.
1 2
4 2
Решение с помощью обратной матрицы:
2 −1
1 −1
Задача 14.
Решите
матричные
уравнения:
X=
,
−3
1
2 −2
2 −1
1 −1
2 −1
3 −2
−13 −6
Y
=
,
Z
=
,
−3
1
2 −2
−3
1
4
1
18 10
2
3
1 −2
5
T =
.
−3 −4
3
4 −1
2 −1
1 −1
Ответ. Y
=
Обычно применяется два варианта решения: применение
−3
1
2 −2
обратной матрицы или сведение к методу Гаусса (используя свойства транспонирования
матриц):
t
t
2 −1
1 −1
2 −3
1 0 2 4
1
2
t
∼
Y =
−3
1
2 −2
−1
1 −1 −2
0 1 1 2
2 4
2 1
t
Y =
⇒ Y =
.
1 2
4 2
Решение с помощью обратной матрицы:
−1 −1
2 −1
2 −1
1 −1
2 −1
Y
=
⇒
−3
1
−3
1
2 −2
−3
1
2 −1
1 −1
Задача 14.
Решите
матричные
уравнения:
X=
,
−3
1
2 −2
2 −1
1 −1
2 −1
3 −2
−13 −6
Y
=
,
Z
=
,
−3
1
2 −2
−3
1
4
1
18 10
2
3
1 −2
5
T =
.
−3 −4
3
4 −1
2 −1
1 −1
Ответ. Y
=
Обычно применяется два варианта решения: применение
−3
1
2 −2
обратной матрицы или сведение к методу Гаусса (используя свойства транспонирования
матриц):
t
t
2 −1
1 −1
2 −3
1 0 2 4
1
2
t
∼
Y =
−3
1
2 −2
−1
1 −1 −2
0 1 1 2
2 4
2 1
t
Y =
⇒ Y =
.
1 2
4 2
Решение с помощью обратной матрицы:
−1 −1
2 −1
2 −1
1 −1
2 −1
1 −1
−1 −1
Y
=
⇒ Y =
⇒
−3
1
−3
1
2 −2
−3
1
2 −2
−3 −2
2 −1
1 −1
Задача 14.
Решите
матричные
уравнения:
X=
,
−3
1
2 −2
2 −1
1 −1
2 −1
3 −2
−13 −6
Y
=
,
Z
=
,
−3
1
2 −2
−3
1
4
1
18 10
2
3
1 −2
5
T =
.
−3 −4
3
4 −1
2 −1
1 −1
Ответ. Y
=
Обычно применяется два варианта решения: применение
−3
1
2 −2
обратной матрицы или сведение к методу Гаусса (используя свойства транспонирования
матриц):
t
t
2 −1
1 −1
2 −3
1 0 2 4
1
2
t
∼
Y =
−3
1
2 −2
−1
1 −1 −2
0 1 1 2
2 4
2 1
t
Y =
⇒ Y =
.
1 2
4 2
Решение с помощью обратной матрицы:
−1 −1
2 −1
2 −1
1 −1
2 −1
1 −1
−1 −1
Y
=
⇒ Y =
⇒
−3
1
−3
1
2 −2
−3
1
2 −2
−3 −2
2 1
⇒ Y =
.
4 2
2 −1
1 −1
Задача 14.
Решите
матричные
уравнения:
X=
,
−3
1
2 −2
2 −1
1 −1
2 −1
3 −2
−13 −6
Y
=
,
Z
=
,
−3
1
2 −2
−3
1
4
1
18 10
2
3
1 −2
5
T =
.
−3 −4
3
4 −1
2 −1
3 −2
−13 −6
Ответ.
Z
=
. Решение методом Гаусса «в два этапа»:
−3
1
4
1
18 10
2 −1
1 −1
Задача 14.
Решите
матричные
уравнения:
X=
,
−3
1
2 −2
2 −1
1 −1
2 −1
3 −2
−13 −6
Y
=
,
Z
=
,
−3
1
2 −2
−3
1
4
1
18 10
2
3
1 −2
5
T =
.
−3 −4
3
4 −1
2 −1
3 −2
−13 −6
Ответ.
Z
=
. Решение методом Гаусса «в два этапа»:
−3
1
4
1
18 10
2 −1 −13 −6
∼
−3
1
18 10
2 −1
1 −1
Задача 14.
Решите
матричные
уравнения:
X=
,
−3
1
2 −2
2 −1
1 −1
2 −1
3 −2
−13 −6
Y
=
,
Z
=
,
−3
1
2 −2
−3
1
4
1
18 10
2
3
1 −2
5
T =
.
−3 −4
3
4 −1
2 −1
3 −2
−13 −6
Ответ.
Z
=
. Решение методом Гаусса «в два этапа»:
−3
1
4
1
18 10
2 −1 −13 −6
1 0 −5 −4
∼
∼
−3
1
18 10
−3 1 18 10
2 −1
1 −1
Задача 14.
Решите
матричные
уравнения:
X=
,
−3
1
2 −2
2 −1
1 −1
2 −1
3 −2
−13 −6
Y
=
,
Z
=
,
−3
1
2 −2
−3
1
4
1
18 10
2
3
1 −2
5
T =
.
−3 −4
3
4 −1
2 −1
3 −2
−13 −6
Ответ.
Z
=
. Решение методом Гаусса «в два этапа»:
−3
1
4
1
18 10
2 −1 −13 −6
1 0 −5 −4
1 0 −5 −4
∼
∼
−3
1
18 10
−3 1 18 10
0 1
3 −2
2 −1
1 −1
Задача 14.
Решите
матричные
уравнения:
X=
,
−3
1
2 −2
2 −1
1 −1
2 −1
3 −2
−13 −6
Y
=
,
Z
=
,
−3
1
2 −2
−3
1
4
1
18 10
2
3
1 −2
5
T =
.
−3 −4
3
4 −1
2 −1
3 −2
−13 −6
Ответ.
Z
=
. Решение методом Гаусса «в два этапа»:
−3
1
4
1
18 10
2 −1 −13 −6
1 0 −5 −4
1 0 −5 −4
∼
∼
−3
1
18 10
−3 1 18 10
0 1
3 −2
3 −2
−5 −4
Z
=
⇒
4
1
3 −2
2 −1
1 −1
Задача 14.
Решите
матричные
уравнения:
X=
,
−3
1
2 −2
2 −1
1 −1
2 −1
3 −2
−13 −6
Y
=
,
Z
=
,
−3
1
2 −2
−3
1
4
1
18 10
2
3
1 −2
5
T =
.
−3 −4
3
4 −1
2 −1
3 −2
−13 −6
Ответ.
Z
=
. Решение методом Гаусса «в два этапа»:
−3
1
4
1
18 10
2 −1 −13 −6
1 0 −5 −4
1 0 −5 −4
∼
∼
−3
1
18 10
−3 1 18 10
0 1
3 −2
t
t
3 −2
−5 −4
3 −2
−5 −4
t
Z
=
⇒
Z =
4
1
3 −2
4
1
3 −2
2 −1
1 −1
Задача 14.
Решите
матричные
уравнения:
X=
,
−3
1
2 −2
2 −1
1 −1
2 −1
3 −2
−13 −6
Y
=
,
Z
=
,
−3
1
2 −2
−3
1
4
1
18 10
2
3
1 −2
5
T =
.
−3 −4
3
4 −1
2 −1
3 −2
−13 −6
Ответ.
Z
=
. Решение методом Гаусса «в два этапа»:
−3
1
4
1
18 10
2 −1 −13 −6
1 0 −5 −4
1 0 −5 −4
∼
∼
−3
1
18 10
−3 1 18 10
0 1
3 −2
t
t
3 −2
−5 −4
3 −2
−5 −4
3 4 −5
3
t
Z
=
⇒
Z =
∼
4
1
3 −2
4
1
3 −2
−2 1 −4 −2
2 −1
1 −1
Задача 14.
Решите
матричные
уравнения:
X=
,
−3
1
2 −2
2 −1
1 −1
2 −1
3 −2
−13 −6
Y
=
,
Z
=
,
−3
1
2 −2
−3
1
4
1
18 10
2
3
1 −2
5
T =
.
−3 −4
3
4 −1
2 −1
3 −2
−13 −6
Ответ.
Z
=
. Решение методом Гаусса «в два этапа»:
−3
1
4
1
18 10
2 −1 −13 −6
1 0 −5 −4
1 0 −5 −4
∼
∼
−3
1
18 10
−3 1 18 10
0 1
3 −2
t
t
3 −2
−5 −4
3 −2
−5 −4
3 4 −5
3
t
Z
=
⇒
Z =
∼
4
1
3 −2
4
1
3 −2
−2 1 −4 −2
1 5 −9
1
∼
∼
−2 1 −4 −2
2 −1
1 −1
Задача 14.
Решите
матричные
уравнения:
X=
,
−3
1
2 −2
2 −1
1 −1
2 −1
3 −2
−13 −6
Y
=
,
Z
=
,
−3
1
2 −2
−3
1
4
1
18 10
2
3
1 −2
5
T =
.
−3 −4
3
4 −1
2 −1
3 −2
−13 −6
Ответ.
Z
=
. Решение методом Гаусса «в два этапа»:
−3
1
4
1
18 10
2 −1 −13 −6
1 0 −5 −4
1 0 −5 −4
∼
∼
−3
1
18 10
−3 1 18 10
0 1
3 −2
t
t
3 −2
−5 −4
3 −2
−5 −4
3 4 −5
3
t
Z
=
⇒
Z =
∼
4
1
3 −2
4
1
3 −2
−2 1 −4 −2
1 5 −9
1
1 5 −9 1
∼
∼
∼
−2 1 −4 −2
0 11 −22 0
2 −1
1 −1
Задача 14.
Решите
матричные
уравнения:
X=
,
−3
1
2 −2
2 −1
1 −1
2 −1
3 −2
−13 −6
Y
=
,
Z
=
,
−3
1
2 −2
−3
1
4
1
18 10
2
3
1 −2
5
T =
.
−3 −4
3
4 −1
2 −1
3 −2
−13 −6
Ответ.
Z
=
. Решение методом Гаусса «в два этапа»:
−3
1
4
1
18 10
2 −1 −13 −6
1 0 −5 −4
1 0 −5 −4
∼
∼
−3
1
18 10
−3 1 18 10
0 1
3 −2
t
t
3 −2
−5 −4
3 −2
−5 −4
3 4 −5
3
t
Z
=
⇒
Z =
∼
4
1
3 −2
4
1
3 −2
−2 1 −4 −2
1 5 −9
1
1 5 −9 1
1 0
1 1
∼
∼
∼
−2 1 −4 −2
0 11 −22 0
0 1 −2 0
2 −1
1 −1
Задача 14.
Решите
матричные
уравнения:
X=
,
−3
1
2 −2
2 −1
1 −1
2 −1
3 −2
−13 −6
Y
=
,
Z
=
,
−3
1
2 −2
−3
1
4
1
18 10
2
3
1 −2
5
T =
.
−3 −4
3
4 −1
2 −1
3 −2
−13 −6
Ответ.
Z
=
. Решение методом Гаусса «в два этапа»:
−3
1
4
1
18 10
2 −1 −13 −6
1 0 −5 −4
1 0 −5 −4
∼
∼
−3
1
18 10
−3 1 18 10
0 1
3 −2
t
t
3 −2
−5 −4
3 −2
−5 −4
3 4 −5
3
t
Z
=
⇒
Z =
∼
4
1
3 −2
4
1
3 −2
−2 1 −4 −2
1 0
1 1
1 1
t
∼ ...
Z =
⇒
0 1 −2 0
−2 0
2 −1
1 −1
Задача 14.
Решите
матричные
уравнения:
X=
,
−3
1
2 −2
2 −1
1 −1
2 −1
3 −2
−13 −6
Y
=
,
Z
=
,
−3
1
2 −2
−3
1
4
1
18 10
2
3
1 −2
5
T =
.
−3 −4
3
4 −1
2 −1
3 −2
−13 −6
Ответ.
Z
=
. Решение методом Гаусса «в два этапа»:
−3
1
4
1
18 10
2 −1 −13 −6
1 0 −5 −4
1 0 −5 −4
∼
∼
−3
1
18 10
−3 1 18 10
0 1
3 −2
t
t
3 −2
−5 −4
3 −2
−5 −4
3 4 −5
3
t
Z
=
⇒
Z =
∼
4
1
3 −2
4
1
3 −2
−2 1 −4 −2
1 0
1 1
1 1
1 −2
t
∼ ...
Z =
⇒ Z=
.
0 1 −2 0
−2 0
1
0
2 −1
1 −1
Задача 14.
Решите
матричные
уравнения:
X=
,
−3
1
2 −2
2 −1
1 −1
2 −1
3 −2
−13 −6
Y
=
,
Z
=
,
−3
1
2 −2
−3
1
4
1
18 10
2
3
1 −2
5
T =
.
−3 −4
3
4 −1
2 −1
3 −2
−13 −6
Ответ.
Z
=
. Решение методом Гаусса «в два этапа»:
−3
1
4
1
18 10
2 −1 −13 −6
1 0 −5 −4
1 0 −5 −4
∼
∼
−3
1
18 10
−3 1 18 10
0 1
3 −2
t
t
3 −2
−5 −4
3 −2
−5 −4
3 4 −5
3
t
Z
=
⇒
Z =
∼
4
1
3 −2
4
1
3 −2
−2 1 −4 −2
1 0
1 1
1 1
1 −2
t
∼ ...
Z =
⇒ Z=
.
0 1 −2 0
−2 0
1
0
Решение с помощью обратной матрицы:
2 −1
1 −1
Задача 14.
Решите
матричные
уравнения:
X=
,
−3
1
2 −2
2 −1
1 −1
2 −1
3 −2
−13 −6
Y
=
,
Z
=
,
−3
1
2 −2
−3
1
4
1
18 10
2
3
1 −2
5
T =
.
−3 −4
3
4 −1
2 −1
3 −2
−13 −6
Ответ.
Z
=
. Решение методом Гаусса «в два этапа»:
−3
1
4
1
18 10
2 −1 −13 −6
1 0 −5 −4
1 0 −5 −4
∼
∼
−3
1
18 10
−3 1 18 10
0 1
3 −2
t
t
3 −2
−5 −4
3 −2
−5 −4
3 4 −5
3
t
Z
=
⇒
Z =
∼
4
1
3 −2
4
1
3 −2
−2 1 −4 −2
1 0
1 1
1 1
1 −2
t
∼ ...
Z =
⇒ Z=
.
0 1 −2 0
−2 0
1
0
Решение с помощью обратной матрицы:
−1 −1
2 −1
−13 −6
3 −2
Z=
⇒
−3
1
18 10
4
1
2 −1
1 −1
Задача 14.
Решите
матричные
уравнения:
X=
,
−3
1
2 −2
2 −1
1 −1
2 −1
3 −2
−13 −6
Y
=
,
Z
=
,
−3
1
2 −2
−3
1
4
1
18 10
2
3
1 −2
5
T =
.
−3 −4
3
4 −1
2 −1
3 −2
−13 −6
Ответ.
Z
=
. Решение методом Гаусса «в два этапа»:
−3
1
4
1
18 10
2 −1 −13 −6
1 0 −5 −4
1 0 −5 −4
∼
∼
−3
1
18 10
−3 1 18 10
0 1
3 −2
t
t
3 −2
−5 −4
3 −2
−5 −4
3 4 −5
3
t
Z
=
⇒
Z =
∼
4
1
3 −2
4
1
3 −2
−2 1 −4 −2
1 0
1 1
1 1
1 −2
t
∼ ...
Z =
⇒ Z=
.
0 1 −2 0
−2 0
1
0
Решение с помощью обратной матрицы:
−1 −1
2 −1
−13 −6
3 −2
Z=
⇒
−3
1
18 10
4
1
1
−1 −1
−13 −6
1 2
⇒ Z=
·
⇒
−3 −2
18 10
11 −4 3
2 −1
1 −1
Задача 14.
Решите
матричные
уравнения:
X=
,
−3
1
2 −2
2 −1
1 −1
2 −1
3 −2
−13 −6
Y
=
,
Z
=
,
−3
1
2 −2
−3
1
4
1
18 10
2
3
1 −2
5
T =
.
−3 −4
3
4 −1
2 −1
3 −2
−13 −6
Ответ.
Z
=
. Решение методом Гаусса «в два этапа»:
−3
1
4
1
18 10
2 −1 −13 −6
1 0 −5 −4
1 0 −5 −4
∼
∼
−3
1
18 10
−3 1 18 10
0 1
3 −2
t
t
3 −2
−5 −4
3 −2
−5 −4
3 4 −5
3
t
Z
=
⇒
Z =
∼
4
1
3 −2
4
1
3 −2
−2 1 −4 −2
1 0
1 1
1 1
1 −2
t
∼ ...
Z =
⇒ Z=
.
0 1 −2 0
−2 0
1
0
Решение с помощью обратной матрицы:
−1 −1
2 −1
−13 −6
3 −2
Z=
⇒
−3
1
18 10
4
1
1
−1 −1
−13 −6
1 2
1 −2
⇒ Z=
·
⇒ Z=
.
−3 −2
18 10
1
0
11 −4 3
2 −1
Задача 14.
Решите
матричные
уравнения:
−3
1
2 −1
1 −1
2 −1
3 −2
−13 −6
Y
=
,
Z
=
,
−3
1
2 −2
−3
1
4
1
18 10
2
3
1 −2
5
T =
.
−3 −4
3
4 −1
2
3
1 −2
5
Ответ.
T =
. Решение методом Гаусса:
−3 −4
3
4 −1
X=
1 −1
2 −2
,
2 −1
Задача 14.
Решите
матричные
уравнения:
−3
1
2 −1
1 −1
2 −1
3 −2
−13 −6
Y
=
,
Z
=
,
−3
1
2 −2
−3
1
4
1
18 10
2
3
1 −2
5
T =
.
−3 −4
3
4 −1
2
3
1 −2
5
Ответ.
T =
. Решение методом Гаусса:
−3 −4
3
4 −1
2
3 1 −2
5
∼
−3 −4 3
4 −1
X=
1 −1
2 −2
,
2 −1
Задача 14.
Решите
матричные
уравнения:
−3
1
2 −1
1 −1
2 −1
3 −2
−13 −6
Y
=
,
Z
=
,
−3
1
2 −2
−3
1
4
1
18 10
2
3
1 −2
5
T =
.
−3 −4
3
4 −1
2
3
1 −2
5
Ответ.
T =
. Решение методом Гаусса:
−3 −4
3
4 −1
2
3 1 −2
5
1 0 −13 −4 −17
∼ ... ∼
−3 −4 3
4 −1
0 1
9
2
13
X=
1 −1
2 −2
,
2 −1
1 −1
Задача 14.
Решите
матричные
уравнения:
X=
,
−3
1
2 −2
2 −1
1 −1
2 −1
3 −2
−13 −6
Y
=
,
Z
=
,
−3
1
2 −2
−3
1
4
1
18 10
2
3
1 −2
5
T =
.
−3 −4
3
4 −1
2
3
1 −2
5
Ответ.
T =
. Решение методом Гаусса:
−3 −4
3
4 −1
2
3 1 −2
5
1 0 −13 −4 −17
−13 −4 −17
∼ ... ∼
T =
.
−3 −4 3
4 −1
0 1
9
2
13
9
2
13
2 −1
1 −1
Задача 14.
Решите
матричные
уравнения:
X=
,
−3
1
2 −2
2 −1
1 −1
2 −1
3 −2
−13 −6
Y
=
,
Z
=
,
−3
1
2 −2
−3
1
4
1
18 10
2
3
1 −2
5
T =
.
−3 −4
3
4 −1
2
3
1 −2
5
Ответ.
T =
. Решение методом Гаусса:
−3 −4
3
4 −1
2
3 1 −2
5
1 0 −13 −4 −17
−13 −4 −17
∼ ... ∼
T =
.
−3 −4 3
4 −1
0 1
9
2
13
9
2
13
Решение с помощью обратной матрицы:
2 −1
1 −1
Задача 14.
Решите
матричные
уравнения:
X=
,
−3
1
2 −2
2 −1
1 −1
2 −1
3 −2
−13 −6
Y
=
,
Z
=
,
−3
1
2 −2
−3
1
4
1
18 10
2
3
1 −2
5
T =
.
−3 −4
3
4 −1
2
3
1 −2
5
Ответ.
T =
. Решение методом Гаусса:
−3 −4
3
4 −1
2
3 1 −2
5
1 0 −13 −4 −17
−13 −4 −17
∼ ... ∼
T =
.
−3 −4 3
4 −1
0 1
9
2
13
9
2
13
Решение с помощью обратной матрицы:
−1 2
3
1 −2
5
T =
⇒
−3 −4
3
4 −1
2 −1
1 −1
Задача 14.
Решите
матричные
уравнения:
X=
,
−3
1
2 −2
2 −1
1 −1
2 −1
3 −2
−13 −6
Y
=
,
Z
=
,
−3
1
2 −2
−3
1
4
1
18 10
2
3
1 −2
5
T =
.
−3 −4
3
4 −1
2
3
1 −2
5
Ответ.
T =
. Решение методом Гаусса:
−3 −4
3
4 −1
2
3 1 −2
5
1 0 −13 −4 −17
−13 −4 −17
∼ ... ∼
T =
.
−3 −4 3
4 −1
0 1
9
2
13
9
2
13
Решение с помощью обратной матрицы:
−1 2
3
1 −2
5
−4 −3
1 −2
5
T =
⇒ T =
⇒
−3 −4
3
4 −1
3
2
3
4 −1
2 −1
1 −1
Задача 14.
Решите
матричные
уравнения:
X=
,
−3
1
2 −2
2 −1
1 −1
2 −1
3 −2
−13 −6
Y
=
,
Z
=
,
−3
1
2 −2
−3
1
4
1
18 10
2
3
1 −2
5
T =
.
−3 −4
3
4 −1
2
3
1 −2
5
Ответ.
T =
. Решение методом Гаусса:
−3 −4
3
4 −1
2
3 1 −2
5
1 0 −13 −4 −17
−13 −4 −17
∼ ... ∼
T =
.
−3 −4 3
4 −1
0 1
9
2
13
9
2
13
Решение с помощью обратной матрицы:
−1 2
3
1 −2
5
−4 −3
1 −2
5
T =
⇒ T =
⇒
−3 −4
3
4 −1
3
2
3
4 −1
−13 −4 −17
⇒ T =
.
9
2
13
Решение задачи
15.



8 −3 −3
2
0 −3
1
2 
1  =  −3
Задача 15. Решите матричное уравнение X ·  1 −1
7
0 −6
1
0
0

 
8 −3 −3
2
0 −3
1
2 
1  =  −3
Задача 15. Решите матричное уравнение X ·  1 −1
7
0 −6
1
0
0
−1
Ответ. X = A · B


2
3 1
X =  −1 −1 0 
2
0 3

Решение задачи
16.


 
60 −4 40
3 −1 2
1 2 3
1 1  =  123 −7 82 
Задача 16. Решите матричное уравнение  4 5 6  X ·  1
186 −10 124
2
0 1
7 8 9

 


60 −4 40
3 −1 2
1 2 3
1 1  =  123 −7 82  .
Задача 16. Решите матричное уравнение  4 5 6  X ·  1
186 −10 124
2
0 1
7 8 9

Ответ. X = A−1 · C · B −1

−1
1 0
X =  2 −2 1 
3
1 2

Спасибо
за
внимание!
e-mail: melnikov@k66.ru, melnikov@r66.ru
сайты: http://melnikov.k66.ru, http://melnikov.web.ur.ru
Вернуться к списку презентаций?