Примеры задач по КИНЕМАТИКЕ 1. Материальная точка
реклама
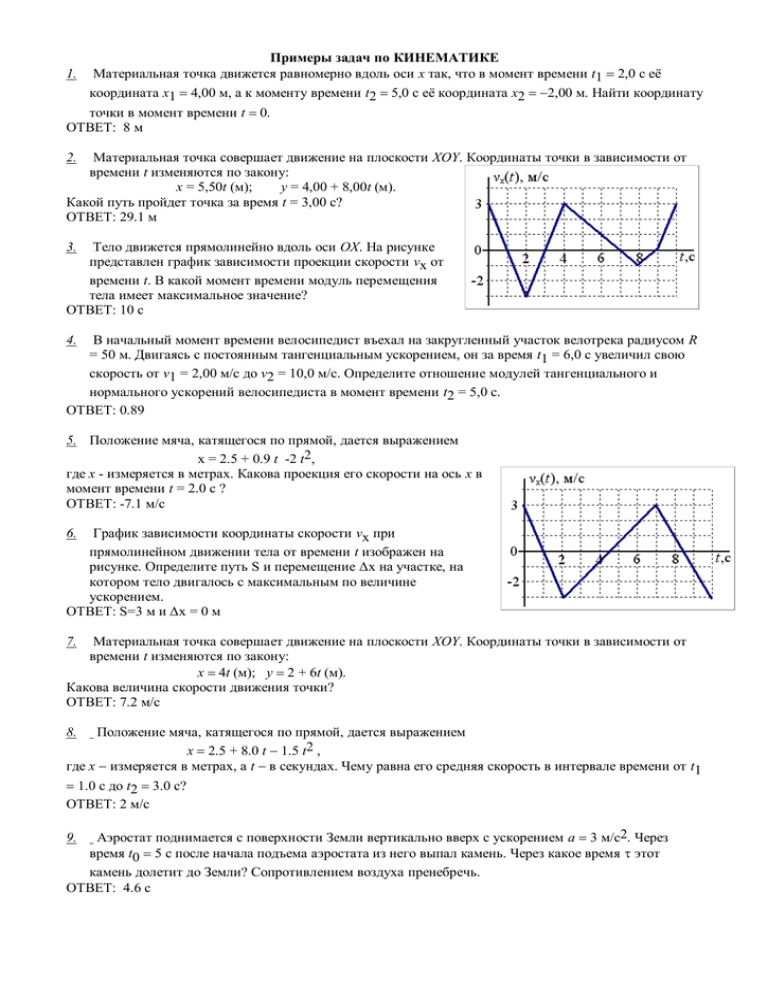
1. Примеры задач по КИНЕМАТИКЕ Материальная точка движется равномерно вдоль оси x так, что в момент времени t1 2,0 с её координата x1 4,00 м, а к моменту времени t2 5,0 c её координата x2 2,00 м. Найти координату точки в момент времени t 0. ОТВЕТ: 8 м 2. Материальная точка совершает движение на плоскости XOY. Координаты точки в зависимости от времени t изменяются по закону: x = 5,50t (м); y = 4,00 + 8,00t (м). Какой путь пройдет точка за время t = 3,00 с? ОТВЕТ: 29.1 м Тело движется прямолинейно вдоль оси OX. На рисунке представлен график зависимости проекции скорости vx от времени t. В какой момент времени модуль перемещения тела имеет максимальное значение? ОТВЕТ: 10 c 3. В начальный момент времени велосипедист въехал на закругленный участок велотрека радиусом R = 50 м. Двигаясь с постоянным тангенциальным ускорением, он за время t1 = 6,0 с увеличил свою скорость от v1 = 2,00 м/с до v2 = 10,0 м/с. Определите отношение модулей тангенциального и нормального ускорений велосипедиста в момент времени t2 = 5,0 с. ОТВЕТ: 0.89 4. 5. Положение мяча, катящегося по прямой, дается выражением х = 2.5 + 0.9 t -2 t2, где х - измеряется в метрах. Какова проекция его скорости на ось x в момент времени t = 2.0 с ? ОТВЕТ: -7.1 м/с График зависимости координаты скорости vx при прямолинейном движении тела от времени t изображен на рисунке. Определите путь S и перемещение Δx на участке, на котором тело двигалось с максимальным по величине ускорением. ОТВЕТ: S=3 м и Δx = 0 м 6. Материальная точка совершает движение на плоскости XOY. Координаты точки в зависимости от времени t изменяются по закону: x 4t (м); y 2 + 6t (м). Какова величина скорости движения точки? ОТВЕТ: 7.2 м/с 7. Положение мяча, катящегося по прямой, дается выражением х 2.5 + 8.0 t 1.5 t2 , где х измеряется в метрах, а t в секундах. Чему равна его средняя скорость в интервале времени от t1 8. 1.0 с до t2 3.0 с? ОТВЕТ: 2 м/с Аэростат поднимается с поверхности Земли вертикально вверх с ускорением a 3 м/с2. Через время t0 5 с после начала подъема аэростата из него выпал камень. Через какое время этот камень долетит до Земли? Сопротивлением воздуха пренебречь. ОТВЕТc 9. 10. Радиус-вектор точки A относительно начала координат меняется по закону: r=t2i-tj, где и постоянные, i и j – орты осей x и y. Найти уравнение траектории точки y(x), зависимости от времени скорости, ускорения и модулей этих величин, а также пройденный частицей путь за время t. 11. Материальная точка совершает движение на плоскости XOY. Координаты точки в зависимости от времени t изменяются по закону: x = 6∙t2 (м); y = sin(2∙π∙t) (м). Найдите скорость точки в момент времени t = 4 с. 12. Самолет имеющий скорость vc=250 км/ч относительно воздуха, держит курс на северо-запад. С востока дует ветер со скоростью vв= 25 км/ч. Определить скорость и направление движения самолета относительно земли. 13. С какой скоростью v и по какому курсу должен лететь самолет, чтобы за время t =1 ч пролететь точно на Север путь s =300 км, если во время полета дует западный ветер со скоростью u =25 км/ч? 14. Какова скорость капель vк отвесно падающего дождя, если шофер легкового автомобиля заметил, что капли дождя не оставляют следа на заднем стекле, наклоненном вперед под углом =60 к горизонту, когда скорость автомобиля vа больше 30км/час? 15. Точка движется по окружности радиусом R с постоянным тангенциальным ускорением a. Через сколько времени после начала движения нормальное ускорение точки будет вдвое больше тангенциального?