Путь, перемещение

МЕХАНИКА
Механика изучает законы и свойства механического движения.
Механическим движением тела называется изменение положения тел или частей тела в пространстве относительно друг друга с течением времени. Очевидно, что характер
движения тела определяется телом, относительно которого рассматривается движение.
Это тело называют телом отсчета. Для задания положения тела необходима также система
координат, а для отсчета времени – способ отсчёта времени. Все это вместе (тело отсчета,
система координат и способ отсчёта времени) образуют систему отсчета. Причем тело отсчета в выбранной системе координат имеет постоянные координаты.
В механике часто используются следующие упрощенные модели реальных тел: абсолютно твердое тело и материальная точка.
Абсолютно твердым телом называется тело, у которого расстояние между двумя любыми
его точками остается постоянным в процессе движения.
Материальной точкой называется тело, размерами и формой которого пренебрегается по
сравнению с другими наиболее характерными размерами, имеющимися в данной рассматриваемой задаче.
Любое механическое движение твердого тела можно представить в виде суперпозиции
(совмещения) двух основных видов механического движения: поступательного и вращательного.
Поступательным движением называется такое движение, при котором любая прямая, жестко связанная с телом, перемещается в пространстве параллельно самой себе. Все точки
тела, движущегося поступательно, двигаются по параллельным траекториям, и в каждый
момент времени имеют одинаковые как по величине, так и по направлению скорости и
ускорения. Поэтому рассмотрение поступательного движения всего тела можно свести к
изучению движения какой-либо точки этого тела.
Вращательным движением называется такое движение, при котором все точки тела описывают в пространстве окружности, центры которых лежат на одной прямой, а сами окружности находятся в плоскостях, перпендикулярных этой прямой.
КИНЕМАТИКА
Кинематика – раздел механики, в котором
изучается механическое движение материального тела без рассмотрения причин, по которым это движение происходит. Введем основные понятия, которыми необходимо будет
пользоваться в дальнейшем.
Будем рассматривать движение тела1,
пользуясь декартовой прямоугольной системой
координат (рис-1). Линия, которую описывает
движущаяся точка в пространстве, называется
траекторией.
Рисунок 1
1
Положение тела на траектории движения однозначно определяется радиус-вектором. Радиусвектор – это вектор, проведенный из начала координат в точку нахождения тела. В процессе
Под телом, в рамках кинематики, мы будем понимать материальную точку
1
движения его длина и направление изменяются, а его начало неподвижно. Если радиусвектор спроецировать на оси координат, то его проекции будут, очевидно, равны соответствующим координатам точки нахождения тела.
Начнем наблюдать за телом, когда оно находится в точке А (рис-2). Пусть в показания ча
сов в этот момент t A , а радиус-вектор тела равен rA . Тело движется вдоль траектории от
точки А к точке В. Когда тело находится в точке В показание часов равно t В , а радиус
вектор rB . Показание часов это и есть момент времени. В большинстве задач момент времени равный нулю будет совпадать с моментом начала движения, то есть часы включаются
в тот момент, когда начинается рассмотрение движения. Тело двигалось из А в В в течении
интервала (промежутка) времени Δt=t B – t A . Если бы показание часов в точке А было равно нулю, то интервал времени был бы равен показанию часов в точке В. Чаще всего так и
поступают при решении задач: за начало отсчета
времени берут момент, когда тело находится в
начальной точке. В начальный момент движения


радиус вектор rA , в конце rB . Разность этих двух
  
векторов Δr=rB -rA называется перемещением тела. Перемещение – вектор, проведенный из начальной точки движения в конечную точку (см.
рис.). Модуль перемещения измеряется в метрах.
Проекции вектора перемещения на оси координат
ОX и ОY равны соответственно: Δrx =Δx=x B -x A ,
Δry =Δy = y B – y A .
Рисунок 2
В общем случае модуль век-
тора перемещения можно найти по формуле:
Δr=
(x B -x A )2 +(y B -y A )2 .
Путь s - сумма длин участков траектории от точки А до точки В, измеряется в мет
рах. Путь величина всегда положительная и неубывающая. В общем случае Δr ≤ S , причём знак равенства справедлив только при движении тела вдоль прямой в одну сторону.
Задача 1.1.
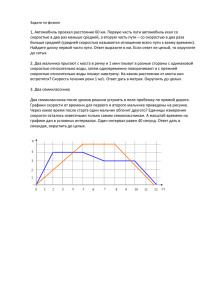
На рис-3 показана траектория A-B-C движения
материальной точки
из А в С. На сколько процентов путь, пройденный
точкой, больше модуля
её перемещения, если АВ = ВС= 20 м, а ОВ = 12
м.
Дано: АВ = ВС = L=20 м; ВО = H = 12 м;
x=

S- Δr
 100%-?
Δr
Рисунок 3

Решение: Путь точки равен S = АВ + ВС = 2L, а модуль перемещения Δr =AC=2 L2 -H 2 .
Отсюда находим a =
Ответ: 25%.
2L-2 L2 -H 2
L- L2 -H 2
⋅ 100% =
⋅ 100% = 25%
2 L2 -H 2
L2 -H 2
2
1.2. Человек прошел по проспекту 240 м, затем повернул на перекрестке и прошел в перпендикулярном
направлении еще 70 м. На сколько процентов путь, пройденный человеком, больше модуля его перемещения? {24%}
1.3. Вертолет пролетел на север в горизонтальном полете 18 км, затем повернул строго на восток и пролетел еще 24 км. Вычислить пройденный путь и модуль полного перемещения. {42 км, 30 км}
1.4. Мяч упал с высоты 3 м вертикально вниз, отскочил от пола и был пойман после отскока на высоте 1 м.
Во сколько раз путь, пройденный мячом, больше модуля перемещения мяча? {2}
1.5. Турист поднялся на возвышенность высотой 10 м и с углом при основании 30°, а затем спустился с
этой же высоты по уклону с углом при основании 60° . Чему равны путь и модуль перемещения туриста?
{31,55 м; 23,1 м}
1.6. Камень, брошенный с высоты 10 м над поверхностью Земли вертикально вверх, достигает максимальной высоты 30 м и падает на Землю. Определить путь, пройденный камнем и модуль его полного перемещения. {50 м; 10 м}
1.7. Самолет пролетел по прямой 600 км, затем повернул под прямым углом и пролетел еще 800 км. Чему
равен модуль вектора перемещения самолета? {103 км}
1.8. Определить путь и перемещение конца минутной стрелки длиной 2 см за 15 мин. {3,14 см; 2,83 см}
1.9. Движущийся автомобиль сделал разворот, описав половину окружности. Во сколько раз путь, пройденный при этом автомобилем, больше модуля перемещения? {1,57}
1.10. Перемещение тела, движущегося по окружности, оказалось равным радиусу окружности. Определить
путь, пройденный телом. Радиус окружности 1 м. {1,05 м}
1.11. Небольшое тело движется по окружности, имеющей радиус 1 м. Определить путь и модуль перемещения тела за время, в течении которого оно совершило 0,25 оборота. {1,57 м; 1,41 м}
1.12. Искусственный спутник движется по круговой орбите радиусом 40000 км с периодом обращения 1 сутки. Определить путь и величину перемещения спутника за 12 часов. {1,257.105 км; 8.104 км}
1.13. Камень бросают с башни высотой 8 м под некоторым углом к горизонту, и он падает на Землю на расстоянии 6 м от башни. Определить модуль полного перемещения камня. {10 м}
1.14. Автомобиль проехал 500 м по прямой горизонтальной дороге. Затем он проехал по мосту, который
представляет собой дугу окружности (радиус окружности 500 м) с углом раствора 600 и далее по прямой проехал еще 500 м. Определить путь, пройденный автомобилем и модуль его перемещения.{1523,3м;1500м}
1.15. Локомотив, двигаясь прямолинейно, проехал путь 3 км, затем совершил поворот, описав четверть окружности радиусом 1 км, и проехал дальше еще 9 км. Вычислить пройденный путь и модуль полного
перемещения. {13,57 км; 10,8 км}
1.16. Тело переместилось из точки А с координатами (-4; 3) в точку В с координатами (4; 3), а затем - в точку
С с координатами (4; -3). Определить его путь и перемещение. Координаты заданы в метрах. {14 м;10
м}
1.17. Тело переместилось из точки с координатами х1 =2 см, у1 = 0 в точку с координатами х2 = 1 см и у2=1
см, а затем - в точку с координатами х3 = -2 см и у3 = -1 см. Постройте график и с его помощью определите путь и модуль перемещения тела. {5,02 см; 4,12 см}
Быстрота изменения положения материальной точки в пространстве с течением времени
характеризуется средней и мгновенной скоростями.

Вектор средней скорости Vср – векторная величина, равная отношению пере Δr
мещения к промежутку времени, за который это перемещение произошло: Vcp =
.
Δt


Вектор средней скорости Vср совпадает по направлению с вектором перемещения Δr .
Средняя скорость прохождения пути (средняя путевая скорость) – скалярная величина,
равная отношению пройденного пути к тому промежутку времени, за который этот путь
пройден:
ΔS S1 +S2 +…+Sn
V =
=
ср Δt
t1 +t 2 +…t n
Совет. Решая задачи на определение средней скорости необходимо помнить очевидную, в
общем-то, вещь: значение средней скорости больше самой минимальной скорости тела на
данном участке и меньше максимальной: Vmin ≤ Vcp ≤ Vmax . Часто учащиеся допускают
ошибку: считают, что средняя скорость является средним арифметическим начальной и
конечной скоростей. Это действительно имеет место в некоторых частных случаях, но
3
пользоваться этим не следует. Единственным определением средней скорости прохождения пути является вышеприведённая формула.
Задача 2.1.
Определить среднюю скорость автомобиля на всем участке движения в следующих двух
случаях:
a) Первую половину пути он движется со скоростью 40 м/с, а вторую половину со скоростью 20 м/с.
b) Первую половину времени автомобиль движется со скоростью 40 м/с, а вторую половину времени со скоростью 20 м/с.
Дано: V1 = 40 м/c; V2 = 20 м/с. Vср1-? Vср2-?
Решение.
a. Обозначим весь путь, пройденный телом за S. Тогда, пользуясь определением средней
S
S
S
, где t1 =
и t2 =
- времена прохождения первой и
2V1
2V2
t1 +t 2
S
2V1V2
м
второй половины пути, соответственно. Тогда Vср1 = =
≅ 26,7
S
S
V1 +V2
c
+
2V1 2V2
скорости, имеем: Vср1 =
b.
Обозначим полное время движения автомобиля за t . Полный путь будет состоять из
t
2
двух частей: первая часть пути S1 =V1 , пройденная автомобилем за первую половину
t
времени со скоростью V1 , и вторая часть пути S2 =V2 , пройденная автомобилем за
2
вторую половину времени со скоростью V2 . По определению средней скорости имеS +S
ем: Vср2 = 1 2 =
t
Ответ: a) 26,7 м/с
t
t
V1 +V2
2
2 = V1 +V2 =30м/с .
t
2
b) 30 м/с.
Задача 2.2.
Поезд прошел путь 200 км. В течение 1 часа он двигался со скоростью 100 км/ч, затем
сделал остановку на время 30 мин. Оставшуюся часть пути он шел со скоростью 40 км/ч.
Определить среднюю скорость движения поезда.
Дано: S = 200 км =2⋅105 м, t1 =1ч=3600 с, t2 =30 мин = 1800 с, V1 = 30 м/с, V2 = 10 м/с;
V ср-?
Решение.
По определению средней скорости
S +S +S
S
V =
= 1 2 3
ср t
t1 + t 2 + t 3
. По условию задачи выделим три
участка. На первом участке S1=V1t1. S2=0 (поезд сделал остановку). Третий участок S3 = S
– (S1+S2) =S-(V1t1+ 0) поезд прошел за время
V =
cp
S
t = 3
3
V3
. Средняя скорость на всем пути
S
=13,7 м/с. .
S-V1t1
t1 +t 2 +
V3
Ответ: 13,7 м/с.
2.3. Велосипедист движется по траектории в форме окружности с постоянной по модулю скоростью. Чему
равно отношение средней скорости прохождения пути, равного половине окружности, к модулю средней скорости перемещения?
{1,57}
2.4. Найти среднюю скорость тела в двух случаях: а) первую четверть времени тело двигалось со скоростью
7,0 м/с, оставшееся время – со скоростью 4,0 м/с; б) первую четверть пути тело двигалось со скоростью
7,0 м/с, оставшуюся часть пути – со скоростью 4,0 м/с. {a) 4,75 м/с; б) 4,48 м/с}
2.5. Найти среднюю скорость автомобиля, если первую треть пути он движется со скоростью 20 м/с, вторую треть пути – со скоростью 24 м/с, а последнюю треть пути со скоростью 30 м/с? {24 м/с}
4
2.6. Первые 20% всего пути тело двигалось со скоростью 10 м/с, следующие 50% пути - со скоростью 12
м/с, оставшуюся часть пути - со скоростью 15 м/с. Найти среднюю скорость движения на всем пути.
{12,25 м/с}
2.7. Первые 25% всего пути тело двигалось со скоростью 3 м/с, вторые 25% всего пути - со скоростью 6 м/с,
оставшуюся часть пути - со скоростью V. Найти эту скорость, если известно, что средняя скорость
движения тела на всем пути оказалась равной 4 м/с. {4 м/с}
2.8. Велосипедист проехал за 5 секунд 40 м, за следующие 10 секунд – 100 м, и за последние 5 сек – 60 м.
Найти среднюю скорость прохождения всего пути. {10 м/с}
2.9. В течение первых 5 часов поезд двигался со средней скоростью 54 км/ч, а затем в течение 4 часов — со
средней скоростью 18 км/ч. Найдите среднюю скорость поезда за все время движения. {10,55 м/с}
2.10. Первые 3/4 времени своего движения поезд шел со скоростью 72 км/ч, остальное время — со скоростью 36 км/ч. Какова средняя скорость движения поезда на всем пути? {17,5 м/с}
2.11. Первую половину пути тело двигалось со скоростью V1, а вторую – со скоростью на 4 м/с большей, чем
V1. Средняя скорость движения тела на всем пути оказалась равной 3 м/с. Найти скорость движения тела на второй половине пути. {6 м/с}
2.12. Средняя скорость поезда на всем пути равна 12 м/с, причем 40% всего пути он двигался со скоростью в
два раза меньшей, чем на оставшемся пути. Каковы скорости поезда на этих участках?
{8,4 м/с;16,8 м/с}
2.13. Первую половину пути поезд шел со скоростью в 1,5 раза большей, чем вторую половину пути. Какова
скорость на каждом участке пути, если средняя скорость прохождения всего пути равна 12 м/с?
{15 м/с, 10м/с}
2.14. Найти среднюю скорость движения тела, если известно, что первую половину пути тело двигалось со
скоростью, меньшей средней скорости на 2 м/с, а вторую – со скоростью, на 3 м/с большей средней
скорости. {12 м/с}
2.15. Первую треть пути автомобиль двигался со скоростью 10 м/с, вторую треть пути – со скоростью , в два
раза меньшей, чем на оставшейся части пути. Найти скорости, с которыми двигался автомобиль на каждом участке, если средняя скорость движения автомобиля на всём пути оказалась равной 15 м/с.
{15м/с, 30м/с.}
2.16. Катер прошел первую половину пути со средней скоростью в три раза большей, чем вторую. Средняя
скорость на всем пути составляет 6 км/ч. Какова средняя скорость катера на первой половине пути?
{3,3 м/с}
2.17. Автомобиль проехал расстояние 30 км с постоянной скоростью 20 м/с, затем разгрузился и вернулся в
начальный пункт со скоростью 25 м/с. Определить время разгрузки, если средняя скорость на всем пути оказалась равной 18 м/c. {10,6 мин}
2.18. Велосипедист, проехав 4 км со скоростью 12 км/ч, остановился и отдыхал в течение 40 мин. Оставшиеся 8 км пути он проехал со скоростью 8 км/ч. Найдите среднюю скорость велосипедиста на всем пути.
{1,66 м/с}
2.19. Автомобиль проехал первую половину пути со скоростью 60 км/ч. Половину времени, затраченного на
прохождение оставшейся части пути он шёл со скоростью 15 км/ч, а другую половину времени – со
скоростью 45 км/ч. Найти среднюю скорость движения автомобиля на всём пути. {9,09 м/с}
Скорость характеризует быстроту движения точки. В процессе движения скорость
может меняться. Мгновенная скорость – скорость точки в данный момент времени. Определяется мгновенная скорость как производная радиус- вектора по времени:



Δr dr
V= lim
= , где dt - бесконечно малый промежуток времени, настолько малый, что
Δt →0 Δt dt

в течение этого промежутка скорость можно считать неизменной, dr - вектор бесконечно
малого перемещения, совершенного телом за время dt .
Мгновенная скорость – векторная величина. Вектор мгновенной скорости направлен
всегда вдоль касательной к траектории движения в интересующей нас точке. Обозначим

проекции вектора V на оси ОX и ОY соответственно VX и VY , тогда справедливо соот2
2
2
ношение: V =VX +VY , непосредственно вытекающее из теоремы Пифагора.
Если в процессе движения модуль и направление вектора мгновенной скорости остаются постоянными, то такое движение называется равномерным. Очевидно, что направление скорости будет постоянным, только если движение тела будет прямолинейным. Так
что равномерным может быть только прямолинейное движение. Оно так и называется –
равномерное прямолинейное движение. В случае прямолинейного равномерного движе5
ния величина скорости определяется известным выражением: V=
ΔS
, где Δt - интервал
Δt
времени, за который тело проходит отрезок пути Δs . Единица измерения скорости – метр
на секунду (м/с).
В ряде задач приходится рассматривать движение тела относительно двух систем отсчёта, которые движутся друг относительно друга. В этом случае справедлив закон сложения скоростей (для скоростей значительно меньших скорости света):
  
V=V0 +V′ ,
 
где V, V′ - скорости тела в неподвижной и движущейся системах отсчёта, соответственно,

а V0 - скорость движущейся системы отсчёта относительно неподвижной.
Задача 3.1.
В безветренную погоду капли дождя оставляют на окне равномерно движущегося поезда
следы, направленные под углом 600 к вертикали. Какова скорость капель относительно
Земли, если скорость движения поезда 15 м/с?
Дано: α = 600 ; V0 =15 м/с. V -?
  

Решение: По закону сложения скоростей V=V0 +V′ , где V - скорость капель относительно неподвижной системы отсчёта-Земли,

V0 - скорость поезда (скорость движущейся системы отсчёта, свя
занной с поездом, относительно неподвижной Земли)), V′ - скорость капель относительно движущейся системы отсчёта (связан1
ной с поездом). Из рисунка 4 видно, что V=V0 ctgα=15
=8,67м/с .
Рисунок 4
3
3.2. Две вагонетки катятся навстречу друг другу со скоростями 0,5 м /с и 0,4 м /с. Через какое время вагонетки столкнутся, если первоначальное расстояние между ними 135 м? {150 с}
3.3. Автомобиль, двигаясь со скоростью 45 км/ч, в течении 10 с прошел такой же путь, какой автобус,
двигающийся в том же направлении с постоянной скоростью, прошел за 25 с. Найдите величину их
относительной скорости. {7,5 м/с}
3.4. Сколько времени сидящий у окна пассажир поезда, идущего со скоростью 54 км/ч, будет видеть проходящий мимо него встречный поезд, скорость которого равна 36 км/ч, а длина – 150 м? {6 c}
3.5. Рыбак, плывя по течению реки с постоянной относительно воды скоростью, проплывая под мостом,
потерял удочки. Через пол часа он заметил пропажу и повернул обратно. На расстоянии 4 км от моста
он встретился с удочками. Определить скорость течения реки. {4 км/ч}
3.6. Моторный катер проходит расстояние между двумя пристанями против течения за 1час. За такое же
время это расстояние проходит по течению плот. За какое время пройдет это расстояние по течению
катер? {20 мин}
3.7. Самолет летит их пункта А в пункт В и обратно со скоростью 600 км/час относительно воздуха.
Сколько времени затратил самолет на весь полет, если вдоль линии полета непрерывно дует ветер постоянного направления со скоростью 20 м/с? Расстояние между пунктами 900 км. {3,04 часа}
3.8. Во сколько раз время проезда одного и того же расстояния на катере туда и обратно по реке больше,
чем по озеру? Скорость течения реки 3 км/ч, скорость катера относительно воды в обоих случаях 10
км/ч. {2,2}
3.9. Скорость движения лодки относительно воды в два раза больше течения реки. Во сколько раз больше
времени занимает поездка между двумя пунктами против течения, чем по течению? {3}
3.10. В безветренную погоду капли дождя оставляют на окне равномерно движущегося поезда следы, направленные под углом 60º к вертикали. Определить скорость капель относительно Земли, если поезд
движется со скоростью 36 км/ч? {5,77 м/с}
3.11. При горизонтальном ветре, скорость которого 10 м/с, капли дождя падают под углом 30º к вертикали.
При какой горизонтальной скорости ветра капли будут падать под углом 60º к вертикали? {30 м/с}
3.12. Какую скорость должен сообщить мотор катеру, чтобы при скорости течения реки 1,2 м/с катер двигался перпендикулярно берегу со скоростью 3,2 м/с? Под каким углом к берегу должна быть направлена эта скорость? {3,42 м/с; 69,40}
6
3.13. Лодка движется перпендикулярно берегу реки. Ее скорость относительно воды равна 2 м/с. Определите время движения лодки к другому берегу, если ширина реки 80 м, а скорость течения 1 м/с. {46,2
c}
3.14. Катер, переправляясь через реку шириной 600 м, двигался перпендикулярно течению реки со скоростью 4 м/с в системе отсчета, связанной с водой. На сколько метров будет снесен катер течением, если скорость течения 1,5 м/с? {225 м}
3.15. Гребец сообщает лодке скорость 2 м/с относительно воды. Под каким углом к течению реки он должен направить лодку, чтобы плыть точно поперек реки, если скорость ее течения 1 м/с? {1200}
3.16. Эскалатор метро спускает неподвижно стоящего человека за 90 с. По неподвижному эскалатору человек спускается за 2 мин. За какое время спустится человек по движущемуся эскалатору? Скорости
движения человека и эскалатора во всех случаях неизменны. {51,4 с}
3.17. Эскалатор метрополитена, двигаясь равномерно, поднимает неподвижно стоящего на нём человека в
течение одной минуты. По неподвижному эскалатору пассажир, двигаясь равномерно, поднимается за
три минуты. Сколько секунд будет подниматься пассажир по движущемуся вверх эскалатору? {45 c}
3.18. Колонна автомашин длиной 2 км движется со скоростью 36 км/ч. Из начала колонны выезжает мотоциклист, который, достигнув ее конца, возвращается обратно. Скорость мотоциклиста постоянна и
равна
54 км/ч. Сколько времени будет в пути и какой путь пройдет мотоциклист пока он снова нагонит начало колонны? {8 мин; 7,2 км}
3.19. Два велосипедиста едут по взаимно перпендикулярным дорогам со скоростями 10,8 км/ч и 14,4 км/ч,
соответственно. Чему равна их относительная скорость? {18 км/ч}
3.20. Две прямые дороги пересекаются под углом 60º. От перекрестка в одну сторону удаляются по ним две
машины: одна со скоростью 60 км/ч, другая со скоростью 80 км/ч. Определить величину скорости, с
которой одна машина удаляется от другой. Перекресток машины прошли одновременно. {72,1 км/ч;
122 км/ч}
Ускорение – векторная величина показывает, как быстро изменяется скорость тела.



ΔV dV
По определению ускорение это производная скорости по времени: a= lim
, где
=
Δt →0 Δt dt
dt - бесконечно малый промежуток времени, в течение которого ускорение можно считать

постоянным, а dV - бесконечно малый вектор изменения скорости.
Если в процессе движения ускорение тела постоянно по модулю и по направлению, такое
движение называют равнопеременным. Равнопеременное движение может быть и прямолинейным и криволинейным. В случае прямолинейного движения можно различать равноускоренное и равнозамедленное движение. При равноускоренном прямолинейном движении направления векторов ускорения и мгновенной скорости совпадают, а при равнозамедленном прямолинейном движении направления этих векторов противоположны.
При равнопеременном движении ускорение можно определить по формуле:
 
 
 V –V
a= B A , где VA , VB - скорости тела, соответственно, в начальной А и конечной В точΔt
ках; Δt = t B - t A - интервал времени движения от точки А до точки В.
Если движение тела криволинейное, то, вообще говоря, ускорение направлено под
некоторым углом к траектории движения (имеется в виду угол между касательной к траектории и вектором ускорения).
Совет. Вообще важно помнить, что направление вектора ускорения не определяет
направление движения тела.
 
 
При решении задач кинематики важно знать зависимости вида: r = r(t) , V = V(t) ,
которые позволяют определить положение и скорость тела в любой момент времени. Это
и есть основная задача кинематики – определить координаты и скорость тела в любой момент времени, зная начальные условия и закон по которому движется тело. Точный вид
этих зависимостей определяется характером движения тела. Рассмотрим случаи равномерного и равнопеременного движения.
Прямолинейное равномерное движение – движение, при котором скорость тела по

стоянна по модулю и по направлению, а ускорение равно нулю: V=const , a=0 .
7
  
При этом радиус вектор тела зависит от времени следующим образом: r=r0 +Vt . Это
уравнение векторное. В скалярном же виде оно будет иметь вид (в проекции на ось ОХ,

направленной параллельно скорости тела): x=x 0 +Vx t , где r0 - радиус вектор тела в на
чальный момент времени t=0 , x 0 - проекция вектора r0 на ось ОХ или, другими словами,
начальная координата тела.
4.1. Две автомашины движутся по дороге с постоянными скоростями 10 м/с и 15 м/с. Начальное расстояние
между машинами равно 1 км. За сколько секунд вторая автомашина догонит первую? {200 с}
4.2. Две автомашины движутся по взаимно перпендикулярным шоссейным дорогам равномерно со скоростями 54 км/ч. и 72 км/ч. На каком расстоянии друг от друга окажутся автомобили через 10 мин. после
встречи у перекрёстка? {15 км}
4.3. По прямому шоссе в одном направлении движутся два мотоциклиста. Скорость первого мотоциклиста
10 м/с, второго 20 м/с. Расстояние между мотоциклистами в первый момент времени равно 200 м. Найти
время и координату места встречи мотоциклистов, приняв за начало отсчета начальное положение второго мотоциклиста.
{20 с; 400м}
4.4. Из города А выехали с одинаковыми скоростями два автомобиля, второй через 12 мин после первого.
Они поочередно, с интервалом в 14 мин, обогнали одного и того же велосипедиста. Во сколько раз скорость автомобилей больше скорости велосипедиста? {7}
4.5. Два тела движутся навстречу друг другу так, что за каждые 10 с расстояние между ними уменьшается на
16 м. Если эти тела будут двигаться в одном направлении с прежними по величине скоростями, то за 5 с
расстояние между ними увеличится на 3 м. С какой скоростью движется каждое из тел?
(1,1 м/с; 0,5
м/с)
Для равнопеременного движения зависимости радиус-вектора и вектора скорости от

  
at 2
  
времени имеют вид: r = r0 +V0 t +
; V=V0 + at . Эти векторные уравнения, будучи спрое2
цированными на оси координат ОX и ОY , имеют вид:
a x t2
,
2
Vx =V0x + a x t
x = x 0 +V0x t +
y = y 0 + V0y t +
a yt2
2
,
Vy =V0y + a y t .
Следствием этих уравнений является еще одно полезное уравнение:
2
2
Vy2 –V0y
Vx2 –V0x
; y=y +
.
x=x +
o
o
2a y
2a x

Здесь x 0 - начальная координаты тела (координата тела в момент времени t = 0 ), V0 вектор начальной скорости тела (вектор скорости в момент времени t = 0 ), V0x , V0y - его

проекции на оси координат. a x , a y - проекции вектора ускорения a на оси координат. В
этих уравнениях x, y - координаты тела в произвольный момент времени t (мгновенные

координаты); V - вектор мгновенной скорости тела (скорости тела в момент времени t );
VX и VY - проекции вектора мгновенной скорости на оси ОX и ОY. Необходимо понимать, что t, x, y, VX , V - переменные величины, а x 0 , y 0 , V0x , V0y , a x , a y - постоянные в
Y
процессе равнопеременного движения (однажды и навсегда заданные в начальной точке
движения). Эти постоянные величины называются начальными условиями.
8
При решении задач кинематики на равнопеременное движение целесообразно
придерживаться следующей последовательности действий:
• Внимательно прочитать задачу, записать краткое условие, определить характер движения тела (прямо- или криволинейное, равномерное или равнопеременное).
• Нарисовать рисунок, на котором отобразить: начальное положение тела, начальную скорость, ускорение тела, примерную траекторию движения. Изобразить положение интересующих нас точек на траектории движения тела, а также отметить координаты этих
точек и скорость тела в этих точках. Наш интерес к этим точкам определен условием задачи. Изобразить на рисунке оси координат. Направления координатных осей выбираются произвольно, но, конечно так, чтобы уравнения для дальнейшего решения выглядели как можно менее громоздко. Также необходимо четко указать начало координат.
Если движение тела прямолинейное, то, очевидно, достаточно выбрать одну ось координат и направить ее вдоль прямой, по которой тело движется.
• Записать кинематические уравнения движения:
a yt2
ax t2
, y = y 0 + V0y t +
, Vx = V0x + a x t , Vy = V0y + a y t .
x = x 0 + V0x t +
2
2
2
2
Vy2 -V0y
Vx2 -V0x
• При необходимости можно применить формулы: x = x +
, y=y +
.
o
o
2a y
2a x
• Определить начальные условия: значения начальных координат ( x 0 , y 0 ), значения проекций начальной скорости ( V0x , V0y ). Определить проекции ускорения ( a x , a y ).
• Подставить значения начальных условий в кинематические уравнения движения. Полученная таким образом система уравнений является системой кинематических уравнений,
приспособленных для решения данной конкретной задачи.
• Рассмотреть интересующие нас точки на траектории движения тела. Определить значения необходимых величин в этих точках (координат, проекций скорости) и подставить
эти значения в полученные ранее кинематические уравнения движения. Теперь получатся уравнения, содержащие не переменные величины: время, координаты и проекции
скорости, а вполне конкретные значения, определяющие ту или иную точку траектории,
в которой находится тело в некоторый конкретный момент времени.
• Решить полученную систему уравнений для данной «особой точки» относительно неизвестных величин. Получить расчетные формулы для искомых величин.
• Произвести проверку размерности (наименование величины).
• Подставить численные значения, сделать расчет и проанализировать полученный результат.
Задача 5.1.
Спуск длиной 100 м лыжник прошел за 20 с, двигаясь с постоянным ускорением 0,3 м/с2.
Найти скорость лыжника в конце пути.
2
Дано: t1 =20 c , x1 =100 м , a = 0,3 м/с . V1 - ?
Уравнение движения лыжника

at 2
  
, уравнение скорости
r = r0 + V0 t +
2
  
V = V0 + at . С учётом начальных условий
x 0 = 0, V0X = V0 , a X = a , проецируя на ось X
имеем:
x = V0 t +
at 2
и
2
9
VX = V0 + at .
Рисунок 5
Интересующая нас точка на траектории движения – это точка
1. В точке 1: t = t1 , x = x1 , Vx = V1 . Подставим значения времени, координаты и скорости для точки 1 в кинематические
уравнения движения. Получим:
at12
,
x1 =V0 t1 +
2
V1 =V0 + at1 .
Решив эту систему уравнений с двумя неизвестными V0 и V1
относительно неизвестной V1 . В результате получим:
2x1 + at12
м
V1 =
=8
2t1
с
.
Графики движения лыжника изображены на рисунке 6.
Ответ: 8 м/с.
Рисунок 6
Задача 5.2.
За 2 с тело прошло путь 10 м, причем скорость увеличилась в 3 раза. Определить ускорение тела и его начальную скорость.
Дано: t1 =2 c , x1 =10 м , V1 = 3V0 . V0 -? a-?
Решение. Кинематические уравнения движения тела и его скорости имеют вид:

at 2
  
, Vx =V0 +at ,
r = r0 + V0 t +
2
и, с учётом начальных условий
x 0 =0, V0x =v 0 , a x =a , в проекции на ось Ох:
Рисунок 7
at 2
,
x=V0 t+
2
10
Vx =V0 +at .
В точке 1 координата тела равна пройденному пути: x=x =10 м , и в момент времени
1
t=t1 =2 c скорость по условию задачи в 3 раза больше начальной: Vx =V1 =3V0 . Подставляя
эти значения, получим для точки 1: x1 =V0 t1 +
Отсюда a=
x1
t12
2
=2,5 м/с , v 0 =
at12
, 3V0 =V0 +at1 .
2
x1
=2,5 м/с .
2t1
Ответ: 2,5 м/с2; 2,5 м/с.
Задача 5.3.
Поезд движется со скоростью 20 м/с. При торможении до полной остановки он прошёл
расстояние в 200 м. Определите время, в течение которого происходило торможение.
Дано:
=
V0 20
=
м / с, x1 200 м; t1 − ?
Решение. Кинематические уравнения движения тела и его скорости имеют вид:

at 2   
  
, V=V0 +at ,
r = r0 + V0 t +
2
и, с учётом начальных условий (см. рисунок 8) x 0 =0, V0x =v 0 , a x = – a , в проекции на ось
Ох:
at 2
,
x=V0 t –
2
Vx =V0 – at .
Рисунок 8
В точке 1 координата тела равна пройденному пути:
x=x =200 м , и в искомый момент времени
1
t = t1 скорость по условию задачи равна нулю (поезд остановился) V=
V=
0.
X
1
Для координаты и скорости в точке 1 имеем:
at 2
=
x1 V0 t1 − 1 ,
2
=
0 V0 − at1 .
В этой системе уравнений две неизвестные: ускорение поезда
a и искомый момент остановки поезда t1 . Исключая ускореVt
2x1
ние получим: x1 = 0 1 , откуда:=
t1 =
20 c .
2
V0
Графики зависимости координаты, проекций скорости и ускорения поезда от времени представлены на рисунке 9.
Ответ: 20 с.
Рисунок 9
11
5.4. Лыжник спускается с горы длиной 180 м. Сколько времени займет спуск, если ускорение лыжника рав{20с}
но 0,5 м/с2, а начальная скорость 4 м/с?
5.5. Тело начинает двигаться равноускоренно вдоль некоторой оси с начальной скоростью 10 м/с. Какой
должна быть величина ускорения, чтобы за 2 с оно сместилось на 10 м относительно начальной точки
движения?
{5 м/с2}
5.6. Торможение поезда метро началось на расстоянии 200 м от станции. На каком расстоянии от станции
окажется поезд, идущий со скоростью 30 м/с, через 7 с после начала торможения с ускорением 5 м/с2?
{112,5 м}
5.7. За две секунды движения тело прошло путь 20 м, при этом его скорость, не меняя направления, увеличилась в 3 раза по сравнению с первоначальной. Определить ускорение тела. {5 м/с2}
5.8. За одну секунду движения тело прошло путь 10 м, при этом его скорость, не меняя направления, увеличилась в 4 раза по сравнению с первоначальной скоростью. Каково было ускорение тела? {2 м/с2}
5.9. Двигаясь с ускорением 0,5 м/с2, тело на пути 60 м увеличило свою скорость в 4 раза. Найдите начальную скорость тела. {12м/с}
5.10. Известно, что точка за 10 с прошла 30 м, причем ее скорость увеличилась в 5 раз. Определить ускорение, считая его постоянным. {0,4 м/с2}
Задача 6.1.
Тело, двигаясь равноускоренно с начальной скоростью V0, приобретает, пройдя некоторое расстояние, скорость V2. Какова была скорость тела V1, когда оно прошло половину
этого расстояния.
Дано: V0 , V2 ; V1 -?
Решение.
Применим к решению этой задачи формулу x = x 0
чек (см. рис): для точки с координатой x1 : x1 =
V22x –V02x
2a x
2
V1x
–V02x
2a x
, и точки с координатой x 2 :
.
Из двух последних уравнений после преобразований имеем: V1 =
Ответ: V1 =
2
Vx2 –V0x
.
2a x
Учитывая, что начальные условия имеют вид:
x 0 = 0, V0x = V0 , a x = a (см. рисунок 10) запишем ее для двух то-
Рисунок 10
x 2 = 2x1 =
+
V02 +V22
.
2
V02 +V22
.
2
Задача 6.2.
Двигаясь равноускоренно, тело проходит за 5 с расстояние 30 см, а за следующие 5 с –
80 см. Определить начальную скорость и ускорение тела.
Дано: x1 =0,3м , t1 =5c , x 2 =1,1 м , t 2 =10 c ; V0 - ?, a - ?
Решение: Уравнение движения тела


a t2
 
, с учётом начальных условий
r = r0 + V0 t +
2
x 0 = 0 , V0x = V0 , a x = a , получим зависимость
Рисунок 11
12
at 2
. Рассмотрим точку 1. В момент времени t = t1
2
at 2
at 2
координата точки равна x1 = V0 t1 + 1 , в момент времени t = t 2 x 2 =V0 t 2 + 2 . Получи2
2
координаты тела от времени: x = V0 t +
ли систему уравнений с неизвестными V0 и a , решая которую получим:
a=
2( x 2 t1 -x1t 2 )
x t 2 -x t 2
2
=0,02 м /с . V0 = 1 2 2 1 =0,01 м/с .
t1t 2 (t 2 -t1 )
t1t 2 (t 2 -t1 )
Ответ: 0,01 м/с, 0,02 м/с2.
Задача 6.3.
Автомобиль, трогаясь с места и двигаясь равноускоренно, первый километр прошел за
6 мин. За какое время он проедет второй километр пути?
Дано: x1 =1км = 1000 м , t1 = 6 мин = 360 с , ∆x = x 2 - x1 = 1 км = 1000 м . Δt-?
Решение.
Движение автомобиля прямолинейное равноускоренное. Совместим начало оси Х с
начальной точкой движения. Начальная координата x 0 =0 , проекция начальной скоРисунок 12
рости на ось V0x =0 (по условию задачи),
проекция ускорения на ось ОX: a x =a . Таким образом, координата автомобиля завиat 2
сит от времени по закону: x =
. На тра2
ектории движения автомобиля нас будут интересовать две точки 1 и 2. Обозначим интервал времени, в течение которого автомобиль проходит второй километр пути Δt . Тогда
показание часов в точке 2 будет равно t 2 = t1 + Δt , а координата точки 2 будет равна
a ( t1 +Δt )
at 2
. Выполнив
x 2 = x1 + Δx . Тогда для точки 1 имеем: x1 = 1 ,а для точки 2: x 2 =
2
2
 x +Δx 
преобразования, получим: Δt = t1  1
–1 ≈ 149,4c .
x1


2
Ответ: 149,4 с.
6.2. Двигаясь равноускоренно без начальной скорости, тело, пройдя некоторое расстояние, приобрело скорость 14 м/с. Чему была равна скорость тела, когда оно прошло половину этого расстояния? {10 м/с}
6.3. Тело, двигаясь равноускоренно с начальной скоростью 1 м/с, приобретает, пройдя некоторое расстояние, скорость 7 м/с. Какова была скорость тела, когда оно прошло половину этого расстояния. {5 м/с}
6.4. Пуля, летящая со скоростью 141 м/с, попадает в дерево и проникает на максимальную глубину 6 см.
Определить скорость пули на глубине 3 см. Движение пули считать равнозамедленным. {100 м/с}
6.5. При торможении от скорости 40 км/ч до полной остановки автомобиль прошел путь 16 м. Какой путь
пройдет этот автомобиль на той же дороге при снижении скорости от 100 км/ч до 60 км/ч? Считать, что
ускорение при торможении постоянно и одинаково в обоих случаях. {64 м}
6.6. С какой скоростью надо бросить камень вдоль горизонтальной поверхности катка, чтобы он, скользя с
ускорением 0,5 м/с2, остановился на расстоянии 100 м от начального положения? {10 м/с}
6.7. Через 4 с после начала торможения скорость автомобиля была вдвое меньше начальной. Через сколько
секунд от начала торможения, скорость автомобиля будет в четыре раза меньше начальной. {6 c
6.8. При взлете разбег самолета длится 25 с. Определить путь, пройденный самолетом по взлетной полосе,
если, пройдя ¾ длины разбега, самолет приобрел скорость 51 м/с. Ускорение самолета считать постоянным. {736 м}
13
6.9. Тело, двигаясь с постоянным ускорением, за первые 2 с прошло 16 м, а за следующие 2 с прошло 8 м.
Определить начальную скорость и ускорение тела. {10 м/с, 2 м/с2}
6.10. При равноускоренном движении тела без начальной скорости путь, пройденный телом за 5-ю секунду
больше пути, пройденного за 1-ю секунду на 10 м. Определить ускорение тела. {2,5 м/с2}
6.11. За пятую секунду равнозамедленного движения тело проходит путь 5 м и останавливается. Определить
начальную скорость и ускорение тела.
{50 м/с, 10 м/с2}
6.12. Тело, двигаясь равноускоренно, за первые 5 с своего движения прошло расстояние 100 м, а за первые
10 с – расстояние 300 м. Определить начальную скорость тела. {10м/с}
6.13. Зa первую секунду равноускоренного движения тело проходит путь равный 1м, а за вторую - 2м. Определить модуль начальной скорости тела. {1м/с}
6.14. Тело, скатывающееся с наклонной плоскости с некоторой начальной скоростью, за первые 3с проходит
2 м, а в последующие три секунды 4 м. Считая движение равноускоренным, определите начальную скорость тела. {1/3 м/с}
6.15. Тело, движущееся прямолинейно, пройдя путь 3 м приобретает скорость 4 м/с, а пройдя еще 4 м приобретает скорость 6 м/с. Определить начальную скорость тела, считая движение равноускоренным. {1 м/с}
6.16. Шарик, пущенный вверх вдоль наклонной плоскости, проходит последовательно два равных отрезка
длиной L каждый и продолжает двигаться дальше. Первый отрезок шарик прошел за τ с, второй за 3τ с.
Найти скорость шарика в конце первого отрезка пути. {5L/6τ}
6.17. Автомобиль, трогаясь с места и двигаясь равноускоренно, первый километр прошел за 6 мин. За какое
время он проедет второй километр пути? {2,49 мин}
6.18. Тело, двигаясь из состояния покоя, проходит 10 м и приобретает скорость 2 м/с. Чему будет равна скорость тела, после того как тело пройдет еще 20 м. Ускорение остается все время постоянным.
{3.46
м/с}
6.19. На последнем километре пути скорость поезда уменьшилась на 10 м/с. Определить изменение скорости
на предпоследнем километре пути. Движение по прямой равнозамедленное. {4 м/с}
Задача 7.1.
Пущенное вверх по наклонной плоскости тело через время 4 с оказалось ниже своего первоначального положения на расстоянии 16 м вдоль плоскости. В этот момент значение
скорости тела было равным 10 м/с. Определить ускорение тела и значение начальной
скорости. Построить графики движения.
Дано: t1 = 4 c , v1 =10 м/с , L=16 м ; V0 -?
Рисунок 13
Решение.
Направим ось ОХ вверх вдоль наклонной
плоскости. Начало оси выберем в первоначальной точке движения. При движении по
наклонной плоскости вектор ускорения направлен вниз вдоль наклонной плоскости (см.
рис 13). Начальные условия:
x 0 = 0 , V0X = V0 , проекция ускорения на ось
ОХ: a x = -a .Тогда проекции на эту ось кине-
матического уравнения движения и его скорости имеют вид: x = V0 t -
at 2
, Vx = V0 - at . В
2
интересующей нас точке 1: t = t1 , x = x1 = - L , Vx = -V1 . Кинематические уравнения в
at12
, -V1 = V0 - at1 . Решая эту систему уравнений, находим:
2
V t -2L
V +V
2
= 2 м/с . Если подставить числа, то кинематические уравa = 0 1 = 3 м/с , v 0 = 1 1
t1
t1
точке 1: –L = V0 t1 -
2
нения движения будут выглядеть так: x = 2t - 1,5t , Vx = 2 - 3t .
Графики этих функций представлены на рисунке 14. Вершина параболы на графике x =
x(t) соответствует координате
14
V02
=
≈ 0,67 м и моменту времени
t′ V0 a ≈ 0,67 c .
2a
Ответ: 3 м/с2, 2 м/с.
=
x′
Рисунок 14
Задача 7.2.
Тело начинает соскальзывать по наклонной плоскости и за 10 с проходит путь, равный
2 м. Считая движение равноускоренным, определить модуль ускорения тела и его скорость в этот момент времени.
Дано: t1 = 10 c , x1 = 2 м , a − ?
Решение.
Движение прямолинейное равноускоренное,
описывается уравнениями:

  
at 2
(1)
r =r0 + V0 t +
2
  
(2)
V
= V0 + at
Вектор ускорения направлен вниз вдоль наРисунок 15
клонной плоскости. Начальная скорость равна
нулю (в условии сказано: «тело начинает со-
15
скальзывать … »). Направим ось координат ОХ вниз вдоль наклонной плоскости (см.
рис.), начало оси выберем в начальной точке движения, начало отсчета времени совместим с началом движения.
Тогда начальные условия для нашей задачи будут иметь вид:
x 0 = 0 , V0x = 0 , a x = a . (3)
Проецируя (1) и (2) на ось ОХ, с учетом значений начальных условий (3) получим кинематические уравнения движения нашего тела:
at 2
, (4)
x=
2
Vx = at . (5)
Нас интересует точка 1 с координатой x = x1 , в которой тело находится в момент времени
t = t1 и имеет скорость Vx = V1 . Подставим эти значения в уравнения (4) и (5) и получим
систему уравнений:
at 2
x1 = 1 , (6)
2
V1 = at1 . (7)
Из (6) находим ускорение:
2x
a = 2 1 . (8)
t1
Подставим (8) в (7) и найдем скорость тела в точке 1:
2x
V1 = 1 . (9)
t1
м
м
Подставим числовые значения в расчетные формулы (8) и (9): a = 0, 04 2 , V1 = 0, 4 .
с
с
2
Ответ: 0,04 м/с ; 0,4 м/с.
Задача 7.3.
Тело, которому была сообщена начальная скорость 10 м/с, движется после этого вдоль
прямой с постоянным ускорением 2 м/с2 и направленным противоположно начальной скорости. Определить путь, пройденный телом за 8 с движения.
м
м
Дано: V0 = 10 , a = 2 2 , t1 = 8c . s - ?
с
с
Решение.
Движение прямолинейное равнопеременное. Описывается уравнениями:

  
at 2
,
(1)
r =r0 + V0 t +
2
  
(1а)
V
=
V0 + at .
Рисунок 16
Начальные условия:
x 0 = 0 , V0x = V0 , a x = −a . Спроецируем (1) и (1а) на ось Х с учетом значений начальных условий получим:
at 2
, (2)
=
x V0 t −
2
V=
V0 − at . (3)
x
Для нахождения пути проследим за движением тела. Из начальной точки тело движется
замедленно, его скорость уменьшается, и в точке 2 (см. рисунок) скорость становится рав16
ной нулю. Затем тело движется в обратном направлении. В момент времени t1 = 8c тело
находится в точке 1. Значение пути зависит от того, куда движется тело в этот момент.
Если скорость его в точке 1 направлена вправо, то путь, пройденный телом к этому моменту равен координате точки 1, то есть s = x1 . Если же скорость тела направлен влево –
это означает, что тело возвращается из точки 2 и путь, пройденный им к этому моменту
равен
s = x 2 + ( x 2 − x1 ) = 2x 2 − x1 . (4)
Определим координату, и скорость тела в момент времени t1 = 8c :
at12
(5)
x1 = V0 t1 −
= 16 м ,
2
м
V1x =
V0 − at1 =
−6 . Проекция скорости тела в точке 1 отрицательна, это значит, что
с
тело в этот момент движется влево. Следовательно, путь определяется формулой (4). Для
нахождения x 2 рассмотрим момент времени t 2 , когда тело находится в точке 2. Скорость
тела в этот момент равна нулю. Запишем кинематические уравнения движения для этой
точки:
at 22
, =
=
x 2 V0 t 2 −
0 V0 − at 2 . Из этой системы уравнений находим:
2
V2
(6)
x2 = 0 .
2a
V2
at 2
Подставим (5) и (6) в (4) получим: s = 0 − V0 t1 + 1 = 34 м .
a
2
Ответ: 34 м.
7.4. Пущенное вверх по наклонной плоскости тело через время 10 с оказалось ниже своего первоначального
положения на расстоянии 20 м вдоль плоскости. В этот момент значение скорости тела было равным 12
м/с. Определить значение начальной скорости. {8 м/с}
7.5. По наклонной доске пустили снизу вверх небольшой шарик. В точке L, находящейся на расстоянии 30
см от начала пути шарик побывал дважды: через 1с и через 2с после начала движения. Определить величину скорости шарика в точке L. {0,15 м/с}
7.6. По наклонной доске скользит вверх небольшой шарик. В точке, находящейся на расстоянии 30 см от
начальной точки, шарик побывал дважды: через 1 с и 3 с после начала движения. Определить расстояние от начальной до верхней точки траектории. {0,4 м}
7.7. Тело, которому была сообщена начальная скорость 5 м/с движется после этого вдоль прямой с постоянным ускорением 2 м/с2, направленном противоположно начальной скорости. В некоторый момент времени модуль скорости тела в 3 раза больше начальной. Определить путь, пройденный телом к этому
моменту. {62,5 м}
7.8. Тело, которому была сообщена начальная скорость 12 м/с, движется после этого вдоль прямой с постоянным ускорением, направленным противоположно начальной скорости, и равным 3 м/с2. Определить
путь, пройденный телом за 6 с движения. {30 м}
7.9. Материальная точка движется прямолинейно с начальной скоростью 10 м/с и постоянным ускорением
5 м/с2, направленном в сторону, противоположную начальной скорости. Определить, во сколько раз
путь, пройденный материальной точкой, будет превышать модуль её перемещения спустя 5 с после начала движения. {2,6}
7.10. Тело, которому сообщена начальная скорость 4 м/с движется вдоль прямой с постоянным ускорением
2 м/с2, направленным противоположно начальной скорости. В некоторый момент времени величина его
скорости становится в 2,5 раза больше начальной скорости. Определить путь, пройденный телом к этому моменту времени. {29 м}
Задача 8.1.
Задачи с использованием графиков
Мотоциклист и велосипедист движутся по прямолинейному участку дороги навстречу друг другу
со скоростями 10 м/с и 5 м/с соответственно. В начальный момент расстояние между ними
17
равно 210 м. Определить: время и место их встречи; в какие моменты времени расстояние между ними равно 120 м; пути, пройденные мотоциклистом и велосипедистом к моменту их встречи.
Задачу решить аналитически и графически.
Дано: V1 = 10 м/с, V2 = 5 м/с, L0 = 210 м, L2 = 120 м; xвстр - ? tвстр - ? t ′ - ? t ′′ - ? S1 - ? S2 - ?
Решение.
Свяжем систему отсчета с землей, приняв за начало координат место нахождения мотоциклиста в начальный момент времени. Обозначим
мгновенные координаты мотоциклиста и велосипедиста x1 и x 2 соответственно; начальные
координаты x 01 и x 02 ; проекции скоростей V1X и
Рисунок 17
V2X . Учитывая, что
=
x 01 =
0; x 02 L=
V=
− V2 и так как ускорения мотоциклиста и велосипедиста
0 ; V1X
1; V2X
равны нулю, уравнения зависимости их координат от времени выглядят следующим образом:
x1 = V1t и x=
L0 − V2 t . (1)
2
В момент встречи x=
x=
x встр и t = t встр , т. е. V1t встр
= L0 − V2 t встр , откуда
1
2
L0
210
=
= 14 c . Подставляя полученное значение в любое уравнение (1) поV1 + V2 10 + 5
V1L0
лучим координату места встречи
=
x встр =
140 м .
V1 + V2
Определим моменты времени, в
которые расстояние между мотоциклистом и велосипедистом равно L1 . Расстояние между телами равно модулю
разности их координат. В нашем случае:
L1 = x1 − x 2 = V1t − L0 + V2 t , это уравнение эквивалентно совокупности уравнений: L1 = V1t′ − L0 + V2 t′ и
=
t встр
− ( V1t′ − L0 + V2 t′) ,
L1 =
L0 − L1
= 6 c (соответствует
V1 + V2
заданному расстоянию между мотоциклистом и велосипедистом до встречи)
L0 + L1
Рисунок 18
и t′′ =
=
22 c (соответствует заV1 + V2
данному расстоянию между мотоциклистом и велосипедистом после встречи).
Определим пути S1 и S2 , пройденные мотоциклистом и велосипедистом до встречи:
V1L0
V2 L0
; S2 V=
=
S1 V=
= 140 м=
= 70 м .
1t встр
2 t встр
V1 + V2
V1 + V2
Графики зависимости координат мотоциклиста и велосипедиста от времени изображены
на рисунке. Эти зависимости имеют вид прямых, наклоненных к оси времени под углами
соответственно α1 и α 2 , причем tgα=
V1X= V1 и tgα2 =V2X =− V2 .
1
откуда
=
t′
8.2. Построить графики движений двух тел, описываемых уравнениями x1= -1 + 2t см и х2 = 2 + t см, в одной
системе координат и по графикам определить, через сколько времени с момента t=0 координаты этих
18
тел станут одинаковыми и какой она будет. Время t выразить в секундах, а координату х — в сантиметрах.
8.3. Зависимость координаты тела от времени задана уравнением X = 1 + 2t - 2,5t2. Определить величину
ускорения тела и величину его скорости через 2 с после начала движения.
{5 м/с2; 8 м/с}
8.4. Используя графики зависимости проекции скорости тела от времени vx=vx(t) (см. рис 19) построить графики зависимости проекции ускорения от времени ax=ax(t) и определить путь, пройденный телом. Движение прямолинейное вдоль оси X.
Рисунок 19
Рисунок 20
Ответ: а) 200 м; б) 110 м; в) 89,1 м; г) 205,5 м. Графики представлены на рисунке.
19
8.5. Используя график зависимости проекции ускорения от времени (рисунок 21) определить среднюю скорость движения тела, если начальная скорость в обоих случаях равна нулю. Движение прямолинейное
вдоль оси X.
Рисунок 21
Ответ: а) 5,8 м/с; б) 3,5 м/с.
Движение тела под действием силы тяжести.
Одним из видов равнопеременного движения является движение под действием силы тяжести, которое, независимо от направления движения, происходит с одним и тем же уско 
рением a=g , направленным вертикально вниз. Для описания этого движения выбирают
прямоугольную систему координат и применяют уравнения равнопеременного движения.
Замечание: при решении задач этого раздела принимать g=10м/с2 и силу сопротивления
воздуха не учитывать.
Движение по вертикали.
Задача 9.1.
С высоты h=4 м над поверхностью Земли бросили камень вертикально вверх с начальной
скоростью V0=10 м/с.. Определить: максимальную высоту, на которую
поднимется камень, время полета камня и скорость с которой он упадет на Землю. Определить путь, пройденный телом.
Дано: h , V0 . H - ? , t 2 - ? , V2 - ? , s - ?
Решение.
Выберем начало оси ОХ на поверхности Земли, а саму ось направим вертикально вверх (рис. 22). Время отсчитываем с момента броска тела. Тогда начальная координата тела x 0 = h ,проекция начальной скорости на
ось ОХ V0x = V0 . Проекция ускорения a x = – g . Тогда проекции на ось
Ох кинематического уравнения движения тела и его скорости имеют
gt 2
вид: x = h + V0 t –
, Vx = V0 – gt . Определим максимальную высоту
2
подъема Н. В этой точке 1 (самой верхней точке траектории) скорость
тела становится равной нулю. Тогда для этого момента времени t1 имеем:
Рисунок 22
H = h + V0 t1 –
чим: H = h +
gt12
, 0 = V0 – gt1 . Исключив из этих уравнений t1 , полу2
V02
.
2g
20
Для определения времени полета и конечной скорости рассмотрим точку 2. Координата
этой точки равна нулю, а проекция скорости отрицательна: x=0 , Vx = – V2 . Тогда
0=h+V0 t 2
–
gt 22
, –V2 =V0 – gt 2 .
2
Из квадратного уравнения для t 2
имеем два корня: t 2 =
V0 ±
V02 +2gh
.
g
Поскольку время не может быть отрицательным (отрицательное время
соответствовало бы событиям, произошедшим до броска тела, а они нам
неизвестны) выбираем такое решение
V0 + V02 +2gh
при котором t 2 >0 t 2 =
.
2
Используя это значение, получим для
скорости падения тела на Землю: V2 = V02 +2gh .
Графики движения тела показаны на
рисунке 23.
9.2. С высокого обрыва без начальной скорости падает камень. Какую скорость он
будет иметь через 3с от начала падения?
{30 м/с}
9.3. В некоторый момент времени скорость
падающего тела равна 6 м/с. Какой будет
скорость тела через 2 с? {26 м/с}
9.4. Шарик отпустили без начальной скорости с высоты 125 м. а) в какой момент
времени шарик упадет на Землю? {5 с}
б) в какой момент времени высота шарика уменьшится в 2 раза? С какой скоростью движется шарик на этой высоте?
{3,54 c; 35,4 м/с} в) в какой момент времени скорость шарика достигнет половиРисунок 23
ны максимальной скорости? На какой высоте он находится в этот момент? {2,5c;
93,75м/с}
9.5. Шарик отпустили без начальной скорости с высоты Н. Через какое время t1 высота, на которой находится шарик, будет составлять половину первоначальной высоты? С какой скоростью V1 движется шарик на этой высоте?
{ t1 = H / g ; V1 = gH }
9.6. Шарик отпустили без начальной скорости с высоты Н. Через какое время t1 после начала движения
скорость шарика будет составлять половину его максимальной скорости? На какой высоте h он будет
находиться в этот момент? { t1 = H / 2g ; h = 3H / 4 }
9.7. Шарик отпустили без начальной скорости с высоты Н. На какой высоте будет находиться шарик в момент времени, равный половине времени падения? Какова его скорость в этот момент?
{ h = 3H / 4 ; v1 = gH / 2 }
9.8. Тело, брошенное вертикально вверх из точки, находящейся над землей на высоте 8 м, падает на землю
через 2 с после броска. С какой скоростью брошено тело?
{6 м/с}
9.9. Тело брошено вертикально вверх с высоты 40 м с начальной скоростью 5 м/с. На какой высоте окажется
тело через 2 с?
{30 м/с}
21
9.10. С высоты 25 м тело брошено вертикально вверх со скоростью 15 м/с. Через сколько секунд оно упадет
на землю? {4,2 c}
9.11. Тело, брошенное вертикально вверх, вернулось на Землю через 5 с. Какова была начальная скорость
тела? На какую высоту оно поднялось? {25 м/с, 31,25 м}
9.12. С какой скоростью надо бросить тело вертикально вверх с поверхности земли, чтобы время от момента
броска до момента падения тела на землю равнялось 3 с? {15 м/с}
9.13. С неподвижного аэростата, находящегося на высоте 1125 м, произведен вертикально вниз выстрел,
причем пуля вылетела со скоростью 200 м/с. За какое время и с какой скоростью пуля достигнет Земли?
{5 c, 250 м/с}
9.14. Тело брошено вертикально вверх с поверхности земли. Во сколько раз скорость тела меньше первоначальной скорости на высоте, составляющей 8/9 максимальной высоты подъема? {3}
Задача 10.1.
Тело брошено вертикально вверх со скоростью 25 м/с. Какой путь пройдет тело за третью секунду своего движения?
Дано: V0 = 25 м/с , t1 = 2 c , t 2 = 3 c ; S -?
Решение.
Движение прямолинейное с постоянным ускорением, равным
ускорению свободного падения и описывается уравнениями:

  
at 2
  
, V=V0 +at . Спроецируем их на ось ОX:
r = r0 + V0 t +
2
ax t2
, Vx =V0x +a x t . Определим начальные услоx=x 0 +V0x t+
2
вия: x 0 = 0, V0x = V0 , a x = - g . Подставляя значения начальных
gt 2
, Vx =V0 - gt . Отметим, что третья
2
секунда полета начинается в момент времени t = t1 = 2 c и закан-
условий, получим: x = V0 t -
чивается в момент t = t 2 = 3c . Значит нужно найти путь, пройденный телом в промежуток времени от t1 до t 2 . В момент
t = t1 тело будет находиться в точке с координатой x = x1 , а в
Рисунок 24
момент t = t 2 в точке с координатой x = x 2 . Определим координаты x1 и x 2 : x1 = V0 t1 -
gt12
gt 2
=30 м , x 2 = V0 t 2 - 2 =30 м .
2
2
Как видно координаты этих точек равны друг другу. То есть это одна точка, в которой тело находилось дважды: сначала, двигаясь вверх (в момент t1 ) затем двигаясь вниз (в момент t 2 ). При этом в некоторый момент t 3 тело находилось в наивысшей точке траектории с координатой x 3 . Таким образом, путь, пройденный телом за третью секунду движе-
ния, будет равен: s = 2 ( x 3 - x1 ) . Координату x 3 определим, рассмотрев точку 3 (скорость в
gt 32
этой точке равна нулю): t = t 3 , x = x 3 , Vx = 0 . Для точки 3 имеем: x 3 = V0 t 3 , 0=V0 -gt 3 .
2
 V2
V02
V0
gt 2 
Найдя t 3 =
, получим: x 3 =
и значение пути: S = 2  0 - V0 t1 + 1  =2,5 м .
2g
g
2 
 2g
Ответ: 2,5 м.
Задача 10.2.
22
Тело падает на Землю с некоторой высоты без начальной скорости. Первую половину
пути тело двигалось со средней скоростью 12,5 м/с. С какой высоты падало тело? С какой скоростью тело падает на Землю? Определить среднюю скорость на всем пути
движения тела.
Дано: Vср1 = 12,5 м/с . H-? V2 - ? Vср - ?
Решение.
Движение прямолинейное равнопеременное. Описывается уравнениями

at 2   
  
, V=V0 +at . Спроецируем эти уравнения на ось ОХ, котоr=r +V t+
0
0
2
рую выберем вертикально вверх, а начало ее на поверхности Земли (см.
рис.), получим:
a t2
x=x + V t + x , Vx =V0x +a x t . Начальные условия:
0x
0
2
x = H, V = 0, a = – g .
0
0x
x
Таким образом, кинематические уравнения движения тела имеют вид:
x=H –
gt 2
, V = – gt . Условием задачи задана средняя скорость движеx
2
ния тела на первой половине пути, то есть от начальной точки с координаH
. Рассмотрим точку 1: в этой
2
H
точке тело находится в момент времени t = t , имеет координату x =
.
1
2
Рисунок 25
H
gt 2
Поэтому для этой точки имеем:
=H- 1 .
2
2
S
Средняя скорость на каком-либо участке пути равна по определению: Vcp = пол .
t пол
H
H
H
В нашем случае: S = , t = t . Таким образом: V =
и t =
. Используя эти
ср1
пол 2
1
пол
1
2t1
2Vср1
той x = H до точки 1 с координатой x =
выражения, получим искомую высоту: H=
2
4Vср1
g
= 62,5 м . Для нахождения скорости в мо-
мент падения на Землю рассмотрим точку 2. Этому соответствует момент времени t = t ,
1
координата x = 0 , скорость Vx = – V2 . Подставив эти значения в уравнения движения, получим для точки 2: 0=H –
gt 22
2H
, V = – gt . Соответственно, t 2 =
и V ≈ -35,36 м/c .
2x
2
2x
2
g
Знак «минус» означает, что скорость в точке 2 направлена вниз. Определим среднюю скорость на всем пути. Полный путь тела S = H , полное время движения t = t и, следопол
вательно, V =
ср
H
=
t2
пол
2
gH
=V
2 ≈ 17,68 м/c .
ср1
2
Обратите внимание: средняя скорость на разных участках одного движения разная.
Ответ: 62,5 м, 35,36 м/с, 17,68 м/с.
10.3. Падающее без начальной скорости тело в последнюю секунду падения прошло путь вдвое больший,
чем в предыдущую секунду. С какой высоты падало тело? {31,25 м}
10.4. Падающее с некоторой высоты без начальной скорости тело прошло последние 25 м пути за 1 с. Найти
высоту, с которой падало тело. {45 м}
23
10.5. Падающее без начальной скорости тело за последнюю секунду своего движения пролетело половину
всего пути. Найти время полета и высоту, с которой упало тело. {3,5 с, 6,25 м}
10.6. Тело падает без начальной скорости с высоты 80 м. Какой путь оно пройдет в последнюю секунду
падения? {35 м}
10.7. Тело падает с высоты 500 м без начальной скорости. Какое расстояние тело пройдет за последнюю
секунду своего падения? {95 м}
10.8. Тело, падающее без начальной скорости с некоторой высоты, прошло последние 30 м за время равное
0,5 с. Определить высоту, с которой начало падать тело, и время падения. {195,31 м}
10.9. Груз падает с некоторой высоты без начальной скорости. За 5 с до падения на Землю величина его
скорости равна 150 м/с. С какой высоты падал груз? {2000 м}
10.10. Тело начало падать с высоты H без начальной скорости. В некоторый момент времени падающее тело
находилось на высоте 1100 м, а спустя 10 с после этого – на высоте 120 м над поверхностью Земли. С
какой высоты H падало тело? {1215,2 м}
10.11. Тело, падающее с некоторой высоты без начальной скорости, за время τ после начала движения проходит расстояние в пять раз меньшее, чем за такой же промежуток времени в конце движения. Найти
( (
) )
высоту H, с которой падало тело. { H =gτ2 11 + 21 / 25 }
10.12. Определить, на сколько метров путь, пройденный падающим без начальной скорости телом, в течении
десятой секунды, больше пути, пройденного телом в течении предыдущей секунды. Начальная скорость тела равна нулю. {10 м}
10.13. Какова максимальная высота, на которую поднимется камень, брошенный вертикально вверх, если
через 1,5 с его скорость уменьшилась вдвое? {45 м}
10.14. Тело брошено с поверхности Земли вертикально вверх с начальной скоростью 50 м/с. Каков модуль
полного перемещения и путь, пройденный телом по истечении 10 с от начала движения? {0; 250 м}
10.15. Камень, брошенный вертикально вверх, дважды был на одной и той же высоте — спустя 0,8 и 1,5 с
после начала движения. Чему равна эта высота? {6 м}
10.16. Тело брошено вертикально вверх с начальной скоростью 21 м/с. Определить время между моментами
прохождения телом половины максимальной высоты. {3 c}
10.17. Тело брошено вертикально вверх со скоростью 30 м/с. Некоторую точку тело проходит дважды с интервалом времени 2 с. Определить высоту этой точки. {40 м}
10.18. Тело брошено вертикально вверх со скоростью 25 м/с. Какой путь пройдет тело за третью секунду
своего движения? {2,5 м}
10.19. С балкона бросают камень вертикально вверх. Через 1 с камень оказывается на максимальной высоте, а
еще через 3 с камень падает на Землю. На какой высоте находится балкон. {40 м}
10.20. С балкона высотой 25 м тело брошено вертикально вверх со скоростью 15 м/с. Какой путь пройдет тело
к моменту падения на Землю? {47,5 м}
10.21. Тело брошено с некоторой высоты вертикально вверх со скоростью 30 м/с. Найдите путь, пройденный
телом за 4 с от начала движения. {50 м}
10.22. Тело брошено с некоторой высоты вертикально вверх со скоростью 20 м/с. Найдите путь, пройденный
телом за 3 с от начала движения. {25 м}
10.23. Тело, падая без начальной скорости, достигает Земли за 4с. За какое время оно достигло бы Земли, если
его бросить с той же высоты вертикально вверх с начальной скоростью 30 м/с? {8 с}
10.24. С вертолета, находящегося на высоте 300 м выпал груз. Через какое время груз достигнет Земли, если
вертолет поднимается со скоростью 5 м/с. {8,3 c}
Криволинейное движение тела под действием силы тяжести.
Задача 11.1.
Тело бросили с высоты h , сообщив ему скорость V0 в горизонтальном направлении. Определить величину скорости и угол, под которым она направлена к горизонту в момент
времени, равный половине времени падения тела на землю.
Дано: h, V0, tA = 0,5⋅tпад . VA- ?, β-?.
Решение.
Тело движется с постоянным ускорением – ускорением свободного падения. Запишем за
at 2   
  
, V=V0 +at . Для
висимость радиус вектора тела и его скорости от времени: r=r0 +V0 t+
2
описания движения тела брошенного горизонтально в поле силы тяжести Земли необхо-
24
димо ввести две оси координат в проекциях на эти оси уравнения движения имеют вид:
a yt2
a x t2
, y = y 0 +V0y t +
, Vx =V0x + a x t Vy =V0y + a y t .
x = x +V t +
0 0x
2
2
Начальные условия для этого случая:
x = 0; y = h; V
0
0
0x
=V ; V
0
0Y
= 0; a = 0; a = – g .
x
Y
Подставляя начальные условия в уравнения
движения получим
gt 2
, Vx = V0 , VY = – gt . Сначала оп0
2
ределим момент времени падения t . Для этого
x=V t , y=h –
пад
рассмотрим точку с координатой y = 0 . Для этой
2
точки имеем соотношение: 0=h –
gt пад
2
, откуда
2h
. Теперь рассмотрим точку A, в которой
g
t пад
. Необнаходится тело в момент времени t =
2
ходимо определить величину скорости V и ее направление в пространстве в этот момент
Рисунок 26
t
пад
=
A
времени (угол β ). Запишем для этого момента соотношения: VAx =V0 , VAy = – g ⋅
гда: VA =
2
2
VAx
+VAy
=
g
V02 +
2 2
t пад
, tgβ=
VAy
VAx
4

2gh 
gh
Ответ: VA = V02 + , α=arctg  –
 .
2
 2V0 
= –
t пад
. То2
gt пад
.
2V0
Задача 11.2.
Тело бросили горизонтально с высоты h=100 м с начальной скоростью 5 м/с. Записать
уравнение траектории движения тела. Определить дальность полета.
Решение.
Зависимости координат брошенного тела от времени, с учетом начальных условий (см. предыдущую
задачу), имеют вид:
gt 2
.
x = V t , y=h –
0
2
Исключая из этих уравнений время (выразив t из
первого уравнения и подставив во второе) получим
зависимость координаты y от координаты x:
gx 2
. Это и есть уравнение траектории.
y= h −
2V02
Рисунок 27
Подставив числа получим: y = 100 − 0, 2 ⋅ x 2 .
При y = 0 , x = L , где L - дальность полета тела.
Подставляя значения координат в уравнение траектории получим: L = V0 2h g =
22,4 м.
Ответ: y = 100 − 0, 2 ⋅ x 2 ; 22,4 м.
25
11.3. Из вертолета, движущегося горизонтально со скоростью 40,0 м/с, на высоте 500 м сброшен груз без
начальной скорости относительно вертолета. На каком расстоянии по горизонтали от места выброса
упадет груз? Сколько времени он будет падать? {400 м; 10 c}
11.4. Камень, брошенный горизонтально со скоростью 15 м/с, упал на землю со скоростью 25 м/с. Сколько
времени длился полет камня? {2c}
11.5. С вышки брошен камень в горизонтальном направлении. Через 2с камень упал на землю на расстоянии
40 м от основания вышки. Определить начальную и конечную скорости камня.
{20 м/с; 28,3 м/с}
11.6. Камень бросили горизонтально с балкона, и через 4 с он упал на Землю на расстоянии 10 м от балкона
(по горизонтали). С какой скоростью брошен камень? {2,5 м/с}
11.7. Пуля вылетает из горизонтально расположенного ружья со скоростью 300 м/с. На каком расстоянии от
места выстрела упадет пуля, если высота ружья над поверхностью Земли равна 1,2 м? {147 м}
11.8. Дальность полета тела, брошенного горизонтально со скоростью 5 м/с, равна высоте, с которой его
бросили. Чему равна эта высота? {5 м}
11.9. Из окна, расположенного на высоте 5 м от земли, горизонтально брошен камень, упавший на расстоянии 8 м от дома. С какой скоростью был брошен камень? {8 м/с}
11.10. Тело, брошенное горизонтально со скоростью 20 м/с упало на землю через 3 с. На каком расстоянии от
точки броска произойдет падение?
{75 м}
11.11. Летящий на высоте 180м со скоростью 100м/с самолёт сбрасывает груз на палубу корабля, идущего в
том же направлении со скоростью 36км/ч. Каким должно быть расстояние (по горизонтали) между самолетом и кораблём, чтобы груз попал на палубу корабля? {540м}
11.12. Тело бросили горизонтально со скоростью 40 м/с с некоторой высоты. Определить величину и направление его скорости через три секунды. {50м/c; arctg(-0,75)= -370}
11.13. Из вертолета, движущегося горизонтально со скоростью 40,0 м/с, на высоте 500 м сброшен груз без
начальной скорости относительно вертолета. С какой скоростью, и под каким углом к горизонту груз
упадет на Землю? {108 м/с; -680}
11.14. Камень, брошенный горизонтально, упал на землю через 0,5 с на расстоянии 5 м по горизонтали от
места бросания. Найти угол между вектором скорости и горизонтом в момент падения. {arctg(-0,5)=26,60}
11.15. Тело бросили горизонтально с некоторой высоты со скоростью 15 м/с. Определить эту высоту, если
относительно горизонта величина угла, под которым тело упало на Землю, равна 300. {3,75 м}
11.16. Тело брошено горизонтально с высоты 20м с некоторой скоростью V0. Найти эту скорость, если известно, что относительно горизонта величина угла, под которым тело упало на Землю, равна 450.
{20 м/с}
11.17. Два камня брошенные горизонтально с разных высот упали в одну точку. Во сколько раз отличаются
начальные скорости камней, если высоты, с которых бросали камни, отличаются в 4 раза. Камни бросают из точек, лежащих на одной вертикали. {16}
11.18. На каком расстоянии друг от друга упали на землю камни, брошенные в одном направлении из точки,
находящейся на высоте 125 м, с горизонтальными скоростями, отличающимися на 16 м/с. {80 м}
11.19. Дальность полета тела, брошенного в горизонтальном направлении, равна половине высоты, с которой
брошено тело. Определить угол, который образует с горизонтом скорость тела при его падении на землю? {-760}
11.20. С самолета, летящего горизонтально на высоте 500 м со скоростью 180 км/час, выпал груз. На какой
высоте скорость груза будет составлять с горизонтом угол 600? {125 м}
11.21. Тело бросили горизонтально с некоторой высоты H со скоростью 10 м/с. Определить эту высоту, если
на высоте 10 м скорость тела составляла с горизонтом угол 600. {25 м}
11.22. Из вертолета, движущегося горизонтально со скоростью 40,0 м/с, на высоте 500 м сброшен груз без
начальной скорости относительно вертолета. Через какое время после выброса его скорость составляла
с горизонтом угол 450? {4 c}
11.23. Тело брошено горизонтально с высоты 40 м с некоторой скоростью V0. Найти эту скорость, если на
высоте 20 м скорость тела составляла с горизонтом угол 450. {20 м/с}
11.24. Тело бросили горизонтально с некоторой высоты со скоростью 10 м/с. Написать уравнение траектории
движения тела, если известно, что на высоте 10 м скорость тела составляла с горизонтом угол 600.
{y = 25 – 0,05.x2 }
11.25. Тело бросили горизонтально с некоторой высоты со скоростью 15 м/с. Написать уравнение траектории
движения тела, если известно, что относительно горизонта величина угла, под которым тело упало на
Землю, равна 300. {y = 3,75 – 0,022.x2}
11.26. Дано уравнение движения тела, брошенного горизонтально: y = 25-0,05.x2. Определить, под каким
углом к горизонту направлена скорость тела на высоте 10м. {-600}
11.27. Тело бросили горизонтально с некоторой высоты со скоростью 15 м/с. Написать уравнение траектории
движения тела в виде y=f(x), если известно, что относительно горизонта величина угла, под которым
тело упало на Землю, равна 300. {y = 3,75 – 0,022·x2}
26
11.28. Написать уравнение траектории движения тела, брошенного горизонтально, которое через 4 с упало на
расстоянии 100 м от места броска. {y = 80 – 0,022·x2}
11.29. Тело брошено горизонтально с высоты 45 м. В некоторый момент времени скорость составляла с горизонтом угол 300, а через 1 с скорость составила с горизонтом угол 600. Под каким углом к горизонту
тело упадет на землю? {-740}
Задача 12.1.
Определить максимальную высоту и дальность полета тела, брошенного с высоты 20 м
от поверхности Земли под углом 600 к горизонту. Начальная скорость тела 30 м/с.
0
Дано: h=20 м, V0 =30 м/с, α=60 ; H-? L-?
Решение.

  
at 2
Кинематические уравнения для движения с постоянным ускорением: r =r0 + V0 t +
,
2
  
V=V +at . Спроецируем эти уравнения на оси координат :
0
a yt2
a x t2
, y = y 0 + V0y t +
, Vx =V0x + a x t , VY = V0Y + a Y t
x=x +V t+
0
0x
2
2
Начальные условия для данной ситуации:
x = 0; y = h ; V =V cosα ; V =V sinα ;
0
0
0x
0
0y
0
a = 0; a = – g ;
x
y
С учетом начальных условий:
gt 2
,
0
2
V =V cosα , V =V sinα-gt . Траекторией
x 0
y
0
движения тела является парабола (рисунок
Рисунок 28
28). В верхней точке параболы касательная
к ней горизонтальна (параллельна оси ОX).
Мгновенная скорость тела направлена по
касательной к траектории движения, следовательно, в верхней точке мгновенная скорость
параллельна оси ОX. Пусть в момент времени t = t H тело находится в точке с координатой
x = V cosα ⋅ t , y= h + V0 sin α ⋅ t −
y = H . В этой точке проекция на ось Y вектора мгновенной скорости VY =0 и уравнения
движения для этой точки имеют вид: H = h + V0 sinα ⋅ t H –
gt 2H
, 0=V0sinα-gt H . Откуда
2
V 2sin 2α
V sinα
получаем: t H = 0
и H=h+ 0
. Для определения дальности полета рассмотрим
2g
2g
точку с координатами x=L; y=0 . Для этой точки уравнения движения будут выглядеть
2
gt L
следующим образом: L=V0cosα ⋅ t L и 0=h+V0sinα ⋅ t L , где t L - момент времени, в
2
который тело находится в рассматриваемой точке (то есть время полета тела). Решая
V0sinα ± V02sin 2α+2gh
последнее уравнение имеем два корня: t L1,2 =
, из которых
g
27
физический смысл имеет только положительный. Таким образом окончательно получаем:
V0sinα+ V02sin 2α+2gh
и
t =
L
g


V0cosα  V0sinα+ V02sin 2α+2gh 


.
L=
g
Подставляя числа получим: H=42,5 м , L ≈ 104 м.
Ответ: 42,5 м, 104 м.
Задача 12.2.
Тело брошено вверх под углом α к горизонту с начальной скоростью V0 . Вывести уравнение траектории движения тела и нарисовать ее для двух случаев:
1) тело брошено с поверхности Земли; 2) тело брошено с высоты h над землей.
Дано: V0 , α, h; y = y(x) .
Решение.
Движение тела будет происходить в вертикальной плоскости (перпендикулярной поверхности
Земли). Для описания такого движения выберем
систему координат следующим образом: ось ОX
направим горизонтально вдоль поверхности земли, ось ОY вертикально вверх. Начало системы
координат выберем на поверхности земли. Мы
будем искать уравнение траектории в виде зависимости координаты y от координаты x , то есть
будем искать функцию вида y = y(x) . Любое
движение в поле силы тяжести земли (независиРисунок 29
мо от направления движения) является движением с постоянным ускорением – ускорением свободного падения. Запишем зависимость радиус вектора тела от времени:

at 2
  
и спроецируем его на оси координат:
r = r +V t +
0
0
2
2
a yt2
axt
и y = y 0 + V0y t +
. Преобразуем эти уравнения для случая, когда
x = x 0 + V0x t +
2
2
бросают с поверхности Земли, определив начальные условия:
x = 0; y = 0 ; V = V cosα ; V0y = V0sinα ; a x = 0; a y = – g ;
0
0
0x
0
gt 2
Подставляя начальные условия, получаем уравнения: x = V0 cosα ⋅ t , y = V0 sinα ⋅ t –
.
2
Эти уравнения определяют траекторию движения тела в параметрической форме. Исключив из них переменную t =
динаты x :
y= –
x
, получим явную зависимость координаты
V0cosα
y от коор-
g
2
x + tgα ⋅ x . Это уравнение является уравнением параболы, проходящей
2
2
2V cos α
0
2
через начало координат, ветви которой направлены вниз (коэффициент при x отрицательный). Парабола изображена на рисунке 29, где показаны также максимальная высота
полета (точка y = H – вершина параболы) и дальность полета (точка x = L, y = 0 ).
28
Рассмотрим второй случай, когда тело бросают с высоты h . В этом случае начальные условия имеют вид: x 0 = 0; y 0 = h ; V0x =V0 cosα ; V0y =V0 sinα ; a x = 0; a y = – g ;
Получим: x=V0 cosα ⋅ t ,
y=h + V sinα ⋅ t –
0
gt 2
. Исключая время
2
получим уравнение траектории:
g
y= –
x 2 + tgα ⋅ x + h . Это урав2
2
2V cos α
0
нение параболы, которая пересекает ось
Y в точке y = h (см. рис 30).
g 2
Замечание. При α=0 y = –
x + h.
2
2V
0
Рисунок 30
Этот случай соответствует броску с
высоты в горизонтальном направлении.
Траектория представляет собой параболу с вершиной в начальной точке.
12.3. Тело брошено с поверхности Земли под углом 300 к горизонту. Полное время полета оказалось равным 2 с. Найти начальную скорость тела.
{20м/с}
12.4. Диск, брошенный с поверхности Земли под углом 450 к горизонту, достиг наибольшей высоты 15м.
Какова наибольшая дальность полета диска? {60 м}
12.5. Снаряд, вылетевший из орудия под углом к горизонту, находился в полете 20 с. Какой наибольшей
высоты достиг снаряд.
{500 м}
12.6. Камень, брошенный с поверхности Земли под углом к горизонту, достиг наибольшей высоты 20 м.
Найдите время полета камня.
{4 с}
12.7. Тело брошено с поверхности Земли под некоторым углом к горизонту. Определить угол, под которым бросили тело, и начальную скорость, если известно, что в наивысшей точке траектории, находящейся на высоте 5 м, тело имело скорость 10м/с. {14,14 м/с; 450}
12.8. Тело брошено с поверхности Земли под некоторым углом к горизонту. Определить угол, под которым тело упало на Землю, если известно, что в наивысшей точке траектории, находящейся на высоте 3,75 м, тело имело скорость 5 м/с.
{-600}
12.9. Тело брошено с поверхности Земли под некоторым углом к горизонту. Определить дальность полёта тела, если известно, что в наивысшей точке траектории, находящейся на высоте 20 м, тело имело
скорость 4 м/с. {16м}
12.10. Тело брошено с поверхности Земли со скоростью 10 м/с под углом 45° к горизонту. Через какое
время оно окажется на высоте, равной половине максимальной?
{0,21 c; 1,21 c}
12.11. Камень, брошенный под углом к горизонту, упал на землю со скоростью10 м/с.Чему равны дальность и высота полета камня, если его максимальная скорость во время полета вдвое больше минимальной скорости?
{8,7 м; 3,75 м}
12.12. Камень брошен с поверхности Земли под углом α к горизонту. Найти отношение дальности полета
к максимальной высоте подъема, если sinα = 0,8. {3}
12.13. Дальность полета тела равна максимальной высоте его подъема над поверхностью Земли. Под каким углом брошено тело с поверхности Земли? {760}
12.14. Камень брошен с поверхности Земли под углом 530 к горизонту. Найти отношение максимальной
высоты подъема к дальности полета.
{0,33}
12.15. Небольшое тело бросают с поверхности Земли со скоростью 100м/с под углом 600 к горизонту. Че{5,8с}
рез какое время скорость тела будет составлять угол 300 с горизонтом?
12.16. Лягушка прыгает под некоторым углом к горизонту и через 0,6 с приземляется на расстоянии 80 см
от места прыжка. Определить скорость лягушки в момент прыжка.
{3,28 м/с}
12.17. Какую минимальную скорость мальчик должен сообщить мячу, чтобы перебросить его на другой
берег реки шириной 12 м. {11 м/с}
12.18. Под каким углом к горизонту брошено тело с поверхности земли, если начальная точка, наивысшая
точка траектории и точка падения на землю образуют равносторонний треугольник. {740}
12.19. Тело брошено с поверхности Земли со скоростью 10 м/с под углом 60° к горизонту. Написать уравнение траектории его движения. {y = -0,2x2 +1,7x}
29
12.20. Из одной и той же точки с поверхности земли одновременно бросили два тела. Первое бросили вертикально вверх со скоростью 6 м/с, второе – под углом 30º к горизонту с такой же по модулю скоростью. Найти расстояние между телами через 0,2 с. {1,2 м}
12.21. С высоты 2 м под углом 450 к горизонту брошен камень, который падает на землю на расстоянии
43 м по горизонтали от места бросания. Найти время полёта камня? {3с}
Движение двух тел.
Задача 13.1.
Тело бросают с поверхности Земли вертикально вверх с начальной скоростью 20 м/с. Одновременно с высоты 50 м над поверхностью Земли бросают второе тело вертикально
вниз с начальной скоростью 5 м/с. Определить время и место их встречи.
- ?, h
−?
v =20 м/c , h=50 м , v =5 м/с . t
01
02
встречи
встречи
Решение.
Уравнения движения тел, с учетом начальных
условий имеют вид (ось ОX направим вертикально вверх, начало оси – на поверхности Земли):
gt 2
, для второго
Для первого тела: =
x V01t −
2
gt 2
.
x =−
h V02 t −
2
В момент встречи t = t встречи координаты тел становятся одинаковыми:
2
2
gt встречи
gt встречи
.
Из
V01t встречи −
=
h − V02 t встречи −
2
2
этого уравнения найдем момент встречи
h
=
t встречи = 2 c . Подставляя t встречи в одно
V01 + V02
из уравнений движения, получим координату
места
встречи:
2
2 ( V01 + V02 ) V01 − gh
=
x встречи =
20 м .
2
2 ( V01 + V02 )
Ответ: 2 с; 20 м.
Рисунок 31
Задача 13.2.
Два тела бросили вертикально вверх с одинаковой скоростью 20 м/с через 1 с одно после
другого. Определить где и когда они встретятся.
Дано: V =20 м/с, τ = 1 с; x встречи − ? ; t встречи − ?
0
Решение.
Здесь главное правильно составить кинематические уравнения движения.
Направим ось координат ОХ вверх, а начало оси координат расположим на поверхности
Земли. Тогда, с учетом начальных условий, кинематические уравнения имеют вид: для
первого тела: x =v t –
1
0
gt 2
gt'2
, для второго тела: x =v t' –
.
2 0
2
2
В первом уравнении t – время, показываемое часами, которые запущены в момент броска
первого тела. Во втором уравнении t' – время, которое показывают часы, запущенные одновременно со вторым телом. Для решения задачи нужно выбрать какие-то одни часы,
например, первые. Для этого запишем связь между показаниями первых и вторых часов.
30
Второе тело брошено через время τ после броска первого тела. Это значит, что в момент
броска второго тела вторые часы показывали момент времени t' = 0 , а первые часы в этот
момент показали момент времени t = τ = 1 c . Очевидно, вторые часы всегда будут отставать от первых на τ = 1 c , так, что можно записать: t' = t – τ . Учитывая это, уравнения
движения будет иметь вид: x =v t –
1
0
g( t – τ)
gt 2
и x =v ( t – τ ) –
2 0
2
2
2
при t ≥ τ . Теперь от-
счет времени t ведется от момента броска первого тела.
Встреча двух тел означает, что их координаты
становятся равными в один и тот же момент
времени. Обозначим этот момент времени
, а координату тел в момент встречи
t=t
встречи
. Тогда:
x =x =x
1
2
встречи
2
gt встречи
,
x
=v t
–
встречи
0 встречи
2
x
встречи
=v
0
(t
встречи – τ
)–
g ( t встречи – τ )
v t
0 встречи
−
2
=v
0
.
2
Приравняв, имеем:
2
gt встречи
2
(t
встречи –τ
)−
g ( t встречи –τ )
. Из последнего уравнения находим
2
2
V
τ
= o + =2,5 c . После чего найдем
g
2
V02 gτ 2
x
=
−
=18,25 м .
встречи
2g
8
t
Рисунок 32
встречи
Графики движения тел изображены на рис. 32.
Ответ: 2,5 с; 18,25 м.
Задача 13.3.
Тело брошено вертикально вверх с начальной скоростью V01 = 15 м/с. Через 1 с вертикально вверх бросают второе тело. Какую начальную скорость V02 нужно сообщить
второму телу, чтобы оба тела упали на Землю одновременно.
Дано: V01 = 15 м/с, τ = 1 с; V02 - ?
Решение.
Кинематические уравнения движения тел имеют вид (см. рис 33):
2
g( t – τ)
gt 2
и x = v ( t – τ) −
.Начало отсчета времени совпаx =v t –
2
02
1 01
2
2
дает с моментом броска первого тела. По условию задачи оба тела падают на Землю в один и тот же момент времени t = t
. Координаты тел
падения
в этот момент равны нулю. Поэтому для момента падения кинематические уравнения движения будут иметь вид:
0=v t
01 падения
2
2
g ( t падения – τ )
gt падения
, 0 = v t падения – τ −
. Приравнивая
−
02
2
2
(
)
правые части уравнений, получим:
Рисунок 33
31
v =
02
2v01 – gτ
2v
= 10 м/с . Причем тела упадут на Землю в момент t
= 01 , то есть через
падения
2
g
3 с после броска первого тела. На рисунке 34 показаны графики движения обоих тел.
Ответ: 10 м/с.
Рисунок 34
Задача 13.4.
С высоты начинает падать без начальной скорости тело. Одновременно с ним с поверхности Земли под углом α бросают другое тело так, чтобы оба тела столкнулись в воздухе. Расстояние по горизонтали между точками бросания равно L. Показать, что угол α
не зависит от начальной скорости V0 второго тела, и определить этот угол, если
H
= 3.
L
Решение:
Напишем уравнения движения обоих тел в проекциях на
оси ОХ и ОY:
gt 2
Для первого тела: x1 = v 0 cosα ⋅ t ; y1 =v 0sinα ⋅ t.
2
gt 2
Для второго тела x 2 = L ; y 2 =H. В момент встречи
2
t = t встр координаты положения тел равны друг другу,
т.е. х1 = х2 и y1 = y2. Следовательно: L=v 0 cosα ⋅ t встр и
v 0sinα ⋅ t встр -
2
gt встр
2
=H-
2
gt встр
2
. Получив t встр =
L
,
v 0 cosα
L
H
=
H . Или tgα= . Из этого следует,
v 0 cosα
L
что угол бросания не зависит от начальной скорости
второго тела. Окончательно tgα= 3 ; α =600.
Ответ: 600
Рисунок 35
имеем v 0sinα ⋅
32
13.5. Два тела свободно падают с разных высот и достигают Земли одновременно. Время падения первого тела 2 с, второго 1 с. Найти разность начальных высот падения первого и второго тел. Начальные
скорости тел равны нулю. {15 м}
13.6. Движение двух материальных точек задано уравнениями X1= 25 + 2t – 4t2 и Х2 = 60 + 2t +0,5t2. В
какой момент времени скорости этих тел будут одинаковыми? {0 c}
13.7. По одному направлению из одной точки одновременно начали двигаться два тела: одно равномерно со скоростью 5 м/с, а другое равноускоренно без начальной скорости с ускорением 2 м/с2. Через
какое время второе тело догонит первое? {5 c}
13.8. Два камня находятся на одной вертикали на расстоянии 20 м друг от друга. В некоторый момент
времени верхний камень бросают вертикально вниз со скоростью 2 м/с, а нижний камень отпускают
без начальной скорости. Через какое время камни столкнутся? Какой путь пройдет к этому моменту
каждый камень?
{10 c; 520 м; 500 м}
13.9. С башни высотой 20 м одновременно бросают два шарика: один вертикально вверх со скоростью
15 м/с, другой вертикально вниз со скоростью 5 м/с. Каков интервал времени, отделяющий моменты
падения шариков на Землю? {2,45 с}
13.10. Из двух точек, находящихся на одной вертикали на расстоянии 50 м, бросили одновременно навстречу друг другу два тела с одинаковой скоростью 5 м/с. Определить, через какое время и на каком расстоянии от верхней точки тела столкнутся. {5 c, 150 м}
13.11. Тело свободно падает с высоты 45 м. Одновременно с высоты 75 м бросили второе тело. Какова начальная скорость второго тела, если оба тела достигли земли одновременно? {10 м/с}
13.12. С какой начальной скоростью нужно бросить вертикально вниз тело с высоты 20 м, чтобы оно упало на землю на 1 с быстрее тела, падающего с той же высоты без начальной скорости? {15 м/с}
13.13. Два тела брошены одновременно, одно – вертикально вверх с высоты 20 м и с начальной скоростью
20 м/с, а другое – вертикально вниз с высоты 120 м и начальной скоростью 20 м/с. Через сколько
времени после начала движения встретятся эти тела? {2,5 с}
13.14. Из точки, расположенной на большой высоте от поверхности земли. одновременно бросают два тела с одинаковой скоростью 20 м/с, первое вертикально вниз, второе вертикально вверх. Через какое
время после броска тела будут находиться на расстоянии 200 м друг от друга? {5 c}
13.15. Первое тело брошено с поверхности земли вертикально вверх с начальной скоростью 5 м/с. В тот
же момент с той же по величине начальной скоростью вертикально вниз из точки, соответствующей
наивысшей точке траектории полета первого тела, брошено второе тело. На какой высоте от поверхности земли встретятся тела? {55 см}
13.16. С крыши с интервалом времени в 1 с падают одна за другой две капли. Определить расстояние между каплями через 2 с после начала падения второй капли. {25 м}
13.17. Стоя на краю скалы высотой 180 м над землей, мальчик выронил камень. Вслед за этим через 1 с он
уже бросил второй камень вертикально вниз с некоторой начальной скоростью. Определить эту
скорость, если оба камня упали на землю одновременно. {31 м/с}
13.18. Два шарика брошены из одной точки с одинаковыми начальными скоростями, равными 5 м/с, вертикально вверх с интервалом времени 0,5 с один после другого. Через какое время после вылета
первого шарика, они встретятся в полете? Сопротивлением воздуха пренебречь. {0,75 с}
13.19. Аэростат опускается вертикально вниз с постоянной скоростью 10 м/с. Из аэростата бросают камень вертикально вверх со скоростью 2 м/с относительно земли. Найти максимальное расстояние
между камнем и аэростатом в процессе движения. {7,2 м/с}
13.20. Из аэростата, опускающегося равномерно вниз со скоростью 5 м/с, в момент нахождения его на высоте 100 м над поверхностью Земли бросили вертикально вниз небольшое тело со скоростью 10 м/с
относительно аэростата. Какой промежуток времени разделяет моменты приземления тела и аэростата? {16,8 м}
13.21. Из аэростата, опускающегося равномерно вниз со скоростью 5 м/с, бросили вертикально вверх небольшое тело со скоростью 10 м/с относительно аэростата. Через какое время после броска тело и
аэростат вновь окажутся на одной высоте? {2 c}
13.22. Аэростат опускается равномерно вниз со скоростью 5 м/с. В какой-то момент из него подбрасывают
вертикально вверх небольшое тело с начальной скоростью 30 м/с относительно аэростата. Какое
расстояние окажется между телом и аэростатом в момент нахождения тела в наивысшей точке своей траектории? {43,75 м}
13.23. Аэростат начинает подниматься с земли равноускоренно вертикально вверх и за 10 с достигает высоты 200 м. Через 5 с после старта из аэростата выпадает камень без начальной скорости относительно него. Какой максимальной высоты достигнет камень? Каким будет расстояние между аэростатом и камнем в момент его падения на землю? {70 м; 231 м}
13.24. Тело с начальной скоростью 20 м/с и ускорением 0,2 м/с2 начинает двигаться из точки А по прямой
в точку В, отстоящую от А на расстоянии 3,46 км. Через 20 с из точки В в точку А начинает равноускоренно двигаться другое тело с начальной скоростью 7 м/с. Через 100 с после начала движения
33
первого тела они встретились. Найти ускорение второго тела и его скорость в момент встречи.
{0,03125 м/с2; 4,5 м/с}
Последовательные этапы движения с различными ускорениями.
Задача 14.1.
Двигатель ракеты, запущенной с поверхности Земли вертикально вверх, сообщает ей постоянное ускорение равное 10 м/с2. В течении какого минимального времени должен проработать двигатель, чтобы ракета достигла максимальной высоты 250 м?
Дано: a = 10 м / с 2 H = 250 м , t min -?
Решение.
Движение ракеты состоит из двух этапов. Первый – это движение с
ускорением a при работающем двигателе (на рисунке слева). Как
только двигатель выключается, ускорение ракеты становится равным ускорению свободного падения, поэтому второй этап – движение с ускорением свободного падения g (на рисунке справа).
При этом ракета еще некоторое время продолжает подниматься до
максимальной высоты H , а затем падает.
На каждом этапе движение ракеты – равноускоренное, поэтому



описывается уравнениями: r = r0 + V0 t +

at 2
2
,
 

V = V + at ,которые
0
будучи спроецированными на ось ОХ имеют вид:
Рисунок 36
2
a t2
x = x + V t + x ;V = V + a t.
0
0x
x
0x
x
2
Рассмотрим первый этап движения ракеты.
Начальные условия для этого этапа: x = 0, V = 0, a = a . С уче0
x
0
том этих условий уравнения движения для первого этапа имеют вид: x =
at 2
, V =at .
x
2
Пусть двигатели выключаются в некоторый момент времени t . К этому мо-
1
1
менту ракета поднимается на высоту h
и приобретает скорость V1 . Рассматat12
ривая точку 1, получим: h=
и
2
V = at . Эти значения будут являться
1
1
начальными для следующего этапа
движения – с ускорением свободного
падения.
Рассмотрим второй этап движения ракеты (начало отсчета времени для этого
этапа выберем в точке 1). Начальные
at12
, V = V = at . Учиусловия: x = h =
0
0
1
1
2
Рисунок 37
тывая это, получим кинематические
уравнения для второго этапа движения
34
at12
gt 2
ракеты (с выключенным двигателем): x=
, V =at – g t . Минимальность
+ at t –
1
x
1
2
2
времени работы двигателя ( t = t ) означает, что высота H = 250 м является для ракеты
1
min
максимальной (скорость ракеты на этой высоте равна нулю). Если время работы двигателя
будет меньше искомого t min , то ракета не долетит до высоты H . Поэтому для точки
2: t = t , x = H , V = 0 . Уравнения движения для этой точки имеют вид:
2
X
gt 22
, 0 = at min – gt 2 . Выражая t , имеем
min 2
2
2
2
at
at 2  a 
2H
=5c.
t = min . Используя это значение, получим: H= min 1+  , откуда t =
min
2
g
2  g
 a
a 1+ 
 g
H=
at 2
min
+ at
t –
График зависимости координаты ракеты от времени показан на рисунке 37 (красная линия
– подъем с ускорением a при работающих двигателях, зеленая – движение под действием
силы тяжести, когда двигатели не работают).
Ответ: 5 с.
14.2. Тело двигалось 20 с равномерно, затем в течении 20 с равноускоренно. Определить скорость равномерного движения, если путь за все время движения равен 275 м, а скорость за второй промежуток
времени удвоилась. {5,5 м/с}
14.3. Автомобиль начинает движение из состояния покоя и проходит путь 120 м. Первые 80 м он движется
равноускоренно, а оставшиеся 40 м – равномерно и проходит их за 2 с. Какова средняя скорость движения автомобиля на всем пути? {12 м/с}
14.4. Автомобиль начинает двигаться с места и двигаясь равноускоренно за 10 с развивает скорость 20 м/с.
Далее он движется равномерно и прямолинейно в течении 5 с. Затем автомобиль тормозит в течении 5
с до полной остановки. Определить путь, пройденный автомобилем. {250 м}
14.5. Тело движется с постоянной скоростью 3 м/с в течение 5 с, после чего начинает двигаться равноускоренно с ускорением 0,2 м/с2. Чему будет равна его скорость через 15 с от начала движения и какой
путь пройдет тело за это время. {5 м/с; 55 м}
14.6. Тело, двигаясь прямолинейно с ускорением 3 м/с2 достигло скорости 15 м/с, а затем двигаясь 25 с
равнозамедленно с некоторым ускорением, остановилось. Определить путь, пройденный телом за все
время движения. Начальная скорость равна нулю. {225 м}
14.7. Мальчик, двигаясь равноускоренно из состояния покоя, съехал на санках с горы длиной 50 м за 10 с, а
затем проехал по горизонтальному участку ещё 25 м до остановки. Найдите ускорение мальчика на
втором участке движения. {2 м/с2}
14.8. Парашютист прыгает с самолёта. Первые 2 с он свободно падает, а затем 20 с опускается с постоянной скоростью до земли. С какой высоты прыгал парашютист? {420 м}
14.9. Двигатель ракеты, взлетевшей вертикально вверх работал в течение 20 с. Ракета, продолжая двигаться
еще некоторое время, достигла максимальной высоты 1,5 км. Найти ускорение ракеты во время работы двигателей. {5 м/с2}
14.10. Двигатели ракеты, запущенной вертикально вверх с поверхности земли работали в течение 10 с и сообщали ракете постоянное ускорение 30 м/с2. Какой максимальной высоты над поверхностью земли
достигнет ракета после выключения двигателей? {6000 м}
14.11. В течение 20 с ракета поднимается с постоянным ускорением 0,8g, после чего двигатели ракеты выключаются. Через какое время после этого ракета упадет на землю? {44 с}
14.12. Тело начинает двигаться вдоль прямой без начальной скорости с постоянным ускорением. Через 30
секунд ускорение тела меняется по направлению на противоположное, оставаясь таким же по величине. Через какое время от начала движения тело вернётся в исходную точку? {102,3 с}
14.13. Тело начинает двигаться вдоль прямой без начальной скорости с постоянным ускорением. Через 28 с
ускорение тела меняется по направлению на противоположное, и уменьшается по величине на 4%.
Через какое время после этого тело вернется в исходную точку?
{70 c}
14.14. Аэростат поднимается с Земли с ускорением 1,5 м/с2 вертикально вверх без начальной скорости. Через 20 с после начала движения аэростата из него выпал предмет. Определить какое расстояние
предмет пролетит за последнюю секунду своего падения. {78,55 м}
35
14.15. Аэростат поднимается с Земли с ускорением 0,5 м/с2 вертикально вверх без начальной скорости. Через 30 с после начала движения аэростата из него выпал предмет. Определить через какое время после
этого предмет окажется на Земле. {8,37 с}
14.16. Аэростат поднимается с постоянной скоростью 6 м/с. На высоте 50 м с него сбрасывают груз без начальной скорости относительно аэростата. Найти время падения груза на землю. Определить его скорость в момент соприкосновения с землей. {3,8 с; 32,2 м/с}
Кинематика равномерного движения по окружности.
Движение по окружности с постоянной по модулю
скоростью – криволинейное движение, траекторией которого является окружность и при котором модуль скорости материальной точки остается постоянным.
Угловая скорость ω – величина, характеризующая быстроту движения тела по окружности, равная отношению угла поворота ϕ радиуса, связанного с точкой, к
промежутку времени ∆t за который этот поворот произошел:
∆ϕ
.
ω=
∆t
Единица измерения угловой скорости – радиан в секунРисунок 38
ду (рад/с). При описании движения тела по окружности
углы измеряются в радианах.
Угловая скорость ω связана с линейной скоростью V формулой
V = ω R.
Период вращения T – время одного полного оборота материальной точки по окружности. Период вращения можно представить в виде:
∆t
T= ,
N
где ∆t - интервал времени, в течении которого происходит N оборотов по окружности.
За время, равное одному периоду, отрезок, соединяющий материальную точку с центром окружности, поворачивается на угол 2π радиан, а тело проходит путь 2πR . С учетом этого связь периода с линейной и угловой скоростями выражается формулами:
2πR
2π
,
V=
ω= .
T
T
Частота вращения ν - величина, численно равная числу оборотов, совершаемых телом за единицу времени (одну секунду), определяется формулой:
N
ν= ,
∆t
и связана с периодом T формулой:
1
ν= .
T
Связь частоты с линейной и угловой скоростями:
V=2πν ⋅ R ; ω=2πν .
Единица измерения периода – секунда (с), единица измерения
частоты обратная секунда (с-1)
Равномерное движение точки по окружности – движение с
ускорением, но это не равноускоренное движение.
36
Рисунок 39
Центростремительное (нормальное) ускорение an – ускорение при равномерном движении по окружности, оно характеризует изменение направления вектора скорости. В каждой точке траектории ускорение направлено к центру окружности – перпендикулярно (по
нормали) к касательной, проведенной к окружности в данной точке (рис-39).
V2
an =
= ω2 R = V ω .
R
Задача 15.1.
Найдите радиус вращающегося колеса, если линейная скорость точки, лежащей на ободе, в 2,5 раза больше линейной скорости точки, лежащей на 3 см ближе к оси колеса.
Дано: ∆r = 3 ⋅ 10-2 м, V1 = 2,5 ⋅ V2 ; V2 , R - ?
Решение.
При вращении диска угловая скорость всех его точек
одинакова. Действительно, за один и тот же интервал
времени отрезки, соединяющие точки 1 и 2 (см. рисунок
40) с центром окружности, поворачиваются на один и тот
же угол. ω1 =ω2
Точка 1 находится на ободе диска и движется по окружности, радиус которой равен радиусу диска. Обозначим его R . Радиус окружности, по которой вращается
точка 2, обозначим r . Из условия задачи следует:
R − r =∆r . Угловые скорости точек 1 и 2 можно выраV 2,5V2
V
зить формулами: ω=1 1=
и ω2 = 2 . Осуществляя
R
R
r
Рисунок 40
5
R
подстановки, получим: r =
и R = ∆r = 5 ⋅10-2 м .
3
2,5
Ответ: 5 см.
Задача 15.2.
Сфера радиусом 1 м вращается вокруг вертикальной оси с частотой 90 об/мин. Определить нормальное ускорение точек сферы, направление на которые из центра сферы составляет угол 600 с вертикалью.
Дано: R=1 м, ν=1,5 с-1 , α=600 ;a n -?
Решение.
Точки сферы, направление на которые из центра сферы составляет угол α с вертикалью, лежат на окружности радиуса R ⋅ sin α (см. рисунок 41). Тогда нормальное ускорение
этих точек равно: a n =ω2 R ⋅ s inα , где ω - угловая скорость
вращения сферы, которая связана с частотой формулой:
ω = 2πν . Из уравнений имеем
a n = 4π 2ν 2 R ⋅ sin α ≈ 76,93 м / с 2 .
Ответ: 76,93 м/с2.
Рисунок 41
37
Задача 15.3.
Стержень длиной 50 см вращается с частотой 36 об/мин вокруг перпендикулярной к нему оси пересекающей линию стержня, при этом один его конец движется с линейной
скоростью 60 см/с. Найдите линейную скорость другого конца стержня.
м
Дано: L=0,5 м,ν =0,6 c-1 ,V1 =0,6 ; V2 -?
с
Решение.
Стержень вращается вокруг оси, перпендикулярной плоскости рисунка и проходящей через точку О. Угловая скорость всех точек вращающегося стержня одинакова и равна ω . Скорости концов
стержня V1 и V2 связаны с угловой скоростью ω
формулами
V1 = ωR1 = 2πν R1 , V2 = ωR 2 = 2πν R 2 . (Здесь учтено,
что ω = 2πν ). Кроме того, выполняется очевидное
соотношение: R1 + R 2 = L , где L - длина стержня.
Складывая уравнения, получим:
V1 +V2 = 2πν ( R1 +R 2 ) = 2πν L , откуда получаем
Рисунок 42
Ответ: 1,284 м/с.
окончательно: V2 =2πν L – V1 ≈ 1, 284
м
.
с
Задача 15.4.
Две материальные точки одновременно начинают движение по окружности из одного
положения в противоположных направлениях. Через какой промежуток времени от начала движения они встретятся, если период обращения одной точки 3 с, а второй – 6 с?
Дано: Т1 = 3 с, Т 2 = 6 с. ∆t - ?
Решение.
К моменту встречи отрезки, соединяющие первую и вторую точки с центром окружности, повернутся на углы ϕ1 и ϕ 2 , соответственно (рисунок 43). Причем, как видно из рисунка ϕ1 + ϕ2 =.
2π
(Период обращения первой точки меньше, значит она движется
быстрее и к моменту встречи пройдет больший путь.)
Из определения угловой скорости следует, что
2π
2π
2π
);
∆t , ϕ2 = ω2 ∆t =
∆t (здесь учтено, что ω =
ϕ1 = ω1∆t =
T1
T
T2
∆t - интервал времени от начала движения до момента встречи.
Рисунок 43
Подставляя эти выражения в исходное, получим:
2π
2π
∆t +
∆t = 2π ,откуда находим искомое время:
T1
T2
TT
∆t = 1 2 = 2 c .
T1 +T2
Ответ: 2 с.
15.5. Двигаясь по окружности с постоянной по модулю скоростью, равной 10 м/с, тело переместилось из
точки 1 в точку 2 по дуге с углом раствора 60°. Найдите модуль изменения скорости тела. {10 м/с}
15.6. Точка движется по окружности с постоянной скоростью 50 см/с. Вектор скорости изменяет направление на 300 за время 2c. Каково нормальное ускорение точки? {0,13 м/с2}
15.7. Колесо велосипеда при равномерном вращении совершает 2,5 оборота за 0,2 с. На какой угол повернется спица колеса за время 0,01 с? {450}
38
15.8. При равномерном вращении колесо повернулось на 2π/3 рад за 7 с. Определить период вращения диска. {21 c}
15.9. На плоскости диска проведена прямая линия от его центра к краю по радиусу. Диск начал равномерно
вращаться, при этом прямая линия повернулась на угол 800 за 4 с. Найти период вращения диска. {18
с}
15.10. Угол поворота колеса, имеющего радиус 0,1 м, изменяется по закону φ = π · t. Найти линейную скорость точек обода колеса. {0,34 м/с}
15.11. Путь, пройденный материальной точкой при ее равномерном движении по окружности, изменяется с
течением времени по закону S = 6,28·t. Найти частоту вращения точки, если радиус окружности равен
10 см. {10 с-1}
15.12. Материальная точка движется по окружности, имеющей радиус 10 см. Пройденный путь зависит от
времени по закону S= A··t, где А = 1 м/с. Найти угловую скорость точки. {10 рад/с}
15.13. Материальная точка движется по окружности, имеющей радиус 10 см. Пройденный путь зависит от
времени по закону S= A·t, где А = 2 м/с. Найти число оборотов, сделанных ею за 5 с движения.
{15,92}
15.14. Диск равномерно вращается вокруг своей оси так, что точки, расположенные на расстоянии 30 см от
оси, проходят за некоторое время путь 4 м. Сколько оборотов за это время сделает диск? {2,12}
15.15. Колесо диаметром 50 см делает 720 оборотов за 4 минуты. Определить линейную скорость точек обода колеса. {9,42 м/с}
15.16. Колесо делает 100 оборотов за 1 мин. Определить период вращения колеса. {0,6 с}
15.17. Как изменится ускорение точек обода колеса при уменьшении периода вращения колеса в 5 раз?
{увеличится в 25 раз}
15.18. Найти угловую скорость искусственного спутника Земли, вращающегося по круговой орбите с периодом обращения 88 мин. Найти линейную скорость движения этого спутника, если известно, что
его орбита расположена на расстоянии 200 км от поверхности Земли. Радиус Земли 6400 км.
{0,001 c-1; 6,6 км/с}
15.19. По краю вращающейся с угловой скоростью ω = 0,1 рад/с карусели радиусом 5 м, шагает мальчик.
Определить нормальное ускорение мальчика, если известно, что поворачивая обратно и шагая с
прежней скоростью, мальчик перестает перемещаться относительно Земли. {0,05 м/с2}
15.20. Сфера радиусом 1 м вращается вокруг вертикальной оси с частотой 90 об/мин. Определить нормальное ускорение точек сферы, направление на которые из центра сферы составляет угол 600 с вертикалью. {77 м/с2}
15.21. Центростремительное ускорение человека, находящегося на карусели на расстоянии 6,4 м от ее центра равно 10 м/с2. Определить линейную скорость человека. {8 м/с}
15.22. Определить модуль скорости точек земной поверхности на экваторе. Радиус Земли принять равным
6400 км. {465 м/с}
15.23. Определить скорость орбитального движения Земли, считая радиус её орбиты равным 150 млн км.
{2,987.104 м/с}
15.24. Велосипедист движется по закруглению дороги радиусом 100 м со скоростью 10 м/с. С каким ускорением он проходит закругление? {1 м/с2}
15.25. Чему равен радиус закругления дороги, если по ней движется автомобиль с центростремительным
ускорением 2 м/с2 при скорости 72 км/ч? {200 м}
15.26. Два танка двигаются навстречу друг другу с одинаковыми по модулю скоростями. Когда расстояние
между ними равно 1,5 км танки, не меняя величин скоростей начинают разворот по окружностям
одинаковых радиусов и через 31,4 с расстояние между ними становится минимальным и равным 500
м. Определить скорость танков. {25 м/с}
15.27. При равномерном подъёме груза с помощью лебедки, диаметр барабана которой равен 18 см, скорость подъёма груза равна 0,9 м/с. Определите частоту вращения барабана. {1,47 с-1}
15.28. Минутная стрелка часов на 20% длиннее секундной. Во сколько раз линейная скорость конца секундной стрелки больше, чем минутной стрелки? {50}
15.29. Минутная стрелка часов в четыре раза длиннее секундной стрелки. Найти отношение линейных скоростей концов названных стрелок. {15}
15.30. Скорость точек рабочей поверхности шлифовального круга не должна превышать100 м/с. Найти предельную частоту вращения круга диаметром 40 см. {79,8 с-1}
15.31. Праща, оружие древних людей, представляет собой камень, привязанный к веревке. Камень вращается по окружности с частотой 2 об/с. Расстояние от центра вращения равно 2 м. Чему будет равна скорость вылетевшего камня. {25,1 м/с}
15.32. Определить радиус маховика и центростремительное ускорение точек на его ободе, если при вращении скорость точек на ободе равна 6 м/с, а точек, находящихся на расстоянии 15 см ближе к оси, равна 5,5м/c. {1,8 м; 20 м/с2}
15.33. Линейная скорость точек обода вращающегося колеса равна 3 м/с. Точки, расположенные на 10 см
ближе к оси, имеют линейную скорость 2 м/с. Каковы радиус и угловая скорость вращения колеса?
{0,3 м;10 с-1}
39
15.34. Стержень длиной 1м вращается с частотой 1 c-1 вокруг оси, проходящей через стержень перпендикулярно ему. Нормальное ускорение одного из концов стержня 16 м/с2. Определить линейную скорость
другого конца. {3,73 м/с}
15.35. Стержень длиной 50 см вращается с частотой 72 об/мин вокруг перпендикулярной к нему оси пересекающей линию стержня, при этом один его конец движется с линейной скоростью 1 м/с. Найдите
линейную скорость другого конца стержня. {2,77 м/с}
Комбинированные задачи
Задача 16.1.
Ось с двумя дисками, жестко закреплёнными на ней и расположенными на расстоянии
0,9 м друг от друга, вращается с частотой 2500 об/мин. Пуля, летящая вдоль оси, пробивает оба диска. При этом отверстие от пули во втором диске смещено относительно
отверстия в первом диске на угол 300. Найти скорость пули.
Дано: n = 2500 об/мин = 125/3 об/с; ϕ = 300 = π/6; L = 0,9 м. Vп - ?
Решение.
Рисунок 44
L
равно времени поворота дисков
Vп
ϕ
L
ϕ
2πnL 2π⋅125⋅0,9⋅6
на угол ϕ: ∆t =
. Отсюда
. Следовательно: Vп =
=
=
= 450 м/с .
2πn
Vп 2πn
ϕ
3⋅π
Время пролёта пулей расстояния между дисками ∆t =
Ответ: 450 м/с.
16.2. С каким периодом вращаются колеса, равномерно движущегося без пробуксовки со скоростью 144
км/ч автомобиля, если их радиус 30 см.
16.3. Тонкостенный шар радиусом 1 м вращается с угловой скоростью 628 рад/с относительно оси, проходящей через его центр. С какой минимальной скоростью должна лететь пробивающая шар пуля, чтобы в оболочке шара было только одно отверстие. Траектория пули проходит сквозь центр шара.
{400 м/с}
16.4. Вагон шириной d, движущийся прямолинейно со скоростью v, был пробит пулей, двигавшейся все
время перпендикулярно плоскости движения вагона. Смещение отверстия в стенках вагона относительно друг друга равно L. Определить скорость движения пули. {Vпули=d∙v/L}
16.5. Волчок, вращаясь с частотой 20 об/с, свободно падает с высоты 5м. Сколько оборотов сделает он за
время падения? Начальная скорость падения волчка равна нулю. {20}
16.6. Пуля, выпущенная из винтовки, попадает во вращающийся с частотой 50 об/с тонкостенный цилиндр
диаметром 20 см. Найдите скорость пули, если выстрел произведен в направлении диаметра цилиндра, а к моменту вылета пули из цилиндра входное отверстие сместилось на 1 см. {628 м/с}
16.7. Мальчик равномерно вращает камень, прикрепленный к легкой веревке, по окружности, лежащей в
вертикальной плоскости. Период вращения 0,25 с. Центр окружности находится на высоте 150 см от
40
поверхности земли. Длина нити 40 см. В тот момент, когда камень находится в верхней точке окружности мальчик отпускает веревку. С какой скоростью камень упадет на Землю. {12 м/с}
16.8. Человек катается на карусели радиусом 15 м. Выпавший из его рук предмет упал на землю на расстоянии 20 м от оси карусели. Определить период вращения карусели. Карусель расположена в горизонтальной плоскости на высоте 3 м от земли. {6,6 c}
41