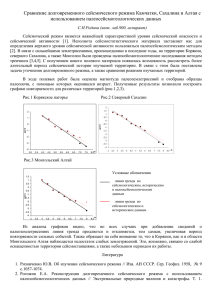
ДИНАМИЧЕСКИЕ ХАРАКТЕРИСТИКИ ОТРАЖЕННЫХ ВОЛН С
реклама

Технологии сейсморазведки, № 2, 2012, с. 12–24 http://ts.ipgg.nsc.ru УДК 550.834 ДИНАМИЧЕСКИЕ ХАРАКТЕРИСТИКИ ОТРАЖЕННЫХ ВОЛН С УЧЕТОМ ВКЛАДА ЭЛЕМЕНТАРНЫХ ГРАНИЦ И ТОЛЩ В.Л. Трофимов, Ф.Ф. Хазиев, В.А. Милашин ООО “Мегацентр-Плюс”, 123298, Москва, ул. Народного Ополчения, 40, корп. 3, Россия, e-mail: trofimvl@gmail.com, hrsgeo@mail.ru, milashin@pcntr.msk.ru На основе разработанного комплекса программ моделирования динамических характеристик отраженных волн изучены особенности формирования интерференционного волнового поля и его динамических параметров в целевом интервале разреза с оценкой вклада элементарных границ и толщ. Для исследования характера проявления интерференции волнового поля и его динамических характеристик вводится понятие “интерференционная матрица вкладов”, представляющая собой прямоугольную таблицу, содержащую количество информации (вклады) об изучаемом свойстве пласта в характеристиках волнового поля или в результатах его преобразований. В интерференционных волновых полях псевдоакустических преобразований, мгновенных динамических параметров (мгновенных амплитуд, фаз и частот) и деконволированной сейсмической записи показан эффект интерференции волн в виде послойного разложения трасс этих характеристик (локальных кривых записей динамических свойств волн). Сейсмическое моделирование волнового поля и его динамических параметров, элементарная граница, вклады границ и толщ, интерференционная матрица вкладов, акустическая жесткость, интерференция волн, псевдоакустические преобразования, мгновенные амплитуды, фазы и частоты, деконволюция DYNAMIC CHARACTERISTICS OF THE REFLECTIONS, WITH THE CONTRIBUTION FROM ELEMENTARY BOUNDARIES AND STRATA HONORED* V.L. Trofimov, F.F. Khaziev, V.A. Milashin Megacenter-Plyus Ltd., 123298, Moscow, Narodnogo Opolcheniya str., 40, Bldg. 3, Russia, e-mail: trofimvl@gmail.com, hrsgeo@mail.ru, milashin@pcntr.msk.ru A software system, developed to model dynamic characteristics of reflections, has facilitated the study of how an interference wavefield and its dynamic parameters are formed in a target interval and how elementary boundaries and strata contribute to the dynamic characteristics. A notion of “contribution interference matrix” is introduced to help study the manifestation of interference wavefield and its dynamic characteristics; the matrix being a rectangular table where information (contribution) on a geologic formation parameter is entered as wavefield characteristics or as a wavefield transformation results. Interference wavefields of acoustic impedance section transforms, of instantaneous amplitudes, phases and frequencies, and of deconvolved seismic data exhibit interference effects as layered decomposition of traces of such characteristics (local curves of wave dynamic parameters). Modeling of seismic wave field and its dynamic parameters, elementary boundary, contributions of boundaries and geologic formations, contribution interference matrix, acoustic impedance, wave interference, acoustic impedance section transforms, instantaneous amplitudes, phases and frequencies, deconvolution ВВЕДЕНИЕ При интерпретации сейсмических данных часто приходится сталкиваться с проблемой адекватного отображения относительно тонких пластов геологического разреза или их совокупностей в соответствующие интервалы сейсмических временных разрезов или кубов сейсмической записи. Особую сложность при этом составляет определение места отображения в сейсмическом волновом поле конкретных временных интервалов изучаемого разреза, непосредственно связанных с продуктивными (нефтенасыщенными) или потенциально продуктивными интервалами геологического разреза. При этом очевидно, что от правильной (адекватной) оценки места и характера отображения последних во многом будут зависеть результаты прогнозирования тех или иных геологических * Текст аннотации приводится в авторской редакции. © В.Л. Трофимов, Ф.Ф. Хазиев, В.А. Милашин, 2012 12 показателей (в первую очередь таких, как литологический состав, коллекторские свойства, нефтегазонасыщенность), а также их качественные и количественные характеристики. На практике часто упускается из виду целый ряд аспектов, которые оказывают существенное влияние на определение места отображения целевых интервалов изучаемого геологического разреза в соответствующие интервалы сейсмического волнового поля. Почти не рассматривается вопрос об имеющемся различии такой важной характеристики, как вертикальная разрешающая способность данных сейсмического волнового поля и методов стандартного каротажа (ГИС). Это расхождение, как известно, можно оценить в ≈1–2 порядка (в зависимости от частотного состава сейсмической записи и глубины исследований), и оно оказывается не в пользу сейсмического метода (можно при этом констатировать существенно более низкую вертикальную разрешающую способность сейсмических записей по сравнению с таковой на кривых методов ГИС). Также (что не менее важно) не раскрывается вопрос о наличии явления всеобъемлющей интерференции на сейсмических трассах (как на реальных, так и на модельных). Данное явление отраженных волн, как известно, выражается и в том, что каждая из амплитуд сейсмической записи (на каждом из временных дискретов) содержит информацию, характеризующуюся реакцией на зондирующий реальную среду сейсмический импульс, которая формируется от вышезалегающих акустических неоднородностей. Как отмечено в [Хазиев и др., 2011], каждая из амплитуд сейсмической записи характеризуется как сумма вкладов от вышезалегающих “элементарных пластов” (с их уникальной интерференцией), отличающая ее от других, проявляющихся на остальных амплитудах сейсмической записи. В то же время информация об акустических неоднородностях реальной среды в форме реакции на зондирующий сейсмический импульс проявляется в форме локальных сейсмических сигналов. Количественно ее можно представить в виде соответствующих кривых вкладов элементарных границ или толщ в суммарную интерференционную сейсмограмму. При этом акустические неоднородности разреза проявляются в виде изменений либо акустической жесткости (произведение плотности на скорость ρV ), либо коэффициентов отражения [Гогоненков, 1987]. Кривые вклада в суммарную интерференционную сейсмограмму отображаются на временном интервале полной длины сейсмического импульса, зондирующего реальную среду, плюс толщина элементарного пласта или толщи (имеется в виду толщина того интервала разреза, который непосредственно анализируется) [Хазиев, Трофимов, 2003; Хазиев и др., 2011]. В результате такой интерференции информация от каждого из элементарных пластов распределяется по временной координате в течение всего прохождения через элементарный пласт (или совокупность таких пластов) зондирующего реальную среду сейсмического импульса, достаточно протяженного по временной или глубинной координате. Следует заметить, что подобная ситуация – только некоторая внешняя часть проблемы “соответствия” (скорее всего, проблемы “различия”) данных сейсморазведки и ГИС. Более детальный анализ влияния геологических параметров разреза на его акустические характеристики и динамику сейсмической записи показывает, что, с одной стороны, на формирование довольно сложной структуры сейсмической записи влияет, как уже отмечено выше, интерференция локальных сейсмических сигналов [Хазиев, Трофимов, 2003; Милашин и др., 2004; Трофимов, Хазиев, 2011; Хазиев и др., 2011]. С другой стороны, следует иметь в виду, что в реальном геологическом разрезе в каждой его точке проявляется результат некоторой “геологической интерференции” геологических показателей, образуя суммарный эффект в результатах геофизических измерений в скважинах. При этом “сейсмическая интерференция” в определенном смысле оказывается отображением соответствующей “геологической интерференции” геологических показателей, также весьма сложной по своей интерференционной структуре. Результат последней визуально можно видеть на результатах автоматизированной обработки данных ГИС [Трофимов и др., 2007; и др.]. Очевидно, что в каждой точке модели реального геологического разреза, особенно в его продуктивных интервалах, содержится та или иная конкретная количественная информация о литологическом составе, коллекторских свойствах и нефтегазонасыщенности пород-коллекторов, которые в той или иной степени оказывают влияние на динамику сейсмической записи. Особенности формы сейсмической записи, как известно, определяются амплитудными и фазовыми характеристиками возбуждаемого в источнике сейсмического импульса, распространяющегося через акустические неоднородности в изучаемой реальной среде. При оценке суперпозиции локальных сейсмических сигналов и ее непосредственного влияния на структуру результирующей интерференционной сейсмической записи следует иметь в виду механизм (процесс) формирования интерференции данных сигналов, который также проявляется и в его различных динамических характеристиках, содержащих гораздо больше информации о среде, чем кинематические. Но сложность распределения этих параметров в динамической структуре сейсмической записи создает проблемы при их использовании, особенно при переходе к изучению в классе тонкослоистых моделей. Это обуславливает необходимость количественного детального анализа динамической структуры сейсмической записи до их применения для целей прогноза или решения обратной динамической задачи сейсмики. Такое исследование также важно и для оценки предельной потенциальной возможности извлечения рассматриваемой характеристики среды из данных наблюдений и их преобразований (например, из выбранной совокупности атрибутов). Наряду с перечисленными проблемами остается нераскрытым вопрос о влиянии на динамические характеристики отраженных волн таких важных геологических показателей изучаемого разреза, как литология, коллекторские свойства и нефтегазонасыщенность. Не изучены вопросы и об информативности самой динамики сейсмической записи в целом, о ее восстанавливаемой или невосстанавливаемой структуре (если при этом иметь в виду возможность получения из динамики сейсмозаписи адекватной модели акустических неоднородностей реальной среды при корректном численном решении обратной динамической задачи сейсмики как результата реализации специального графа обработки сейсмических данных, включающего в себя процедуру сейсмической инверсии по исходным сейсмограммам и окончательным временным разрезам или кубам сейсмической записи [Трофимов и др., 2009] и влиянии на структуру волнового поля различных волн-помех. Неизученной остается также проблема “слабых” сейсмических сигналов [Милашин и др., 2004], которая имеет непосредственное отношение к оценке вклада в сейсмическое волновое поле вышеотмеченных геологических факторов (показателей), таких как литология, коллекторские свойства и нефтегазонасыщенность. Очевидно, что многие из перечисленных проблем не изучены в полной мере, но их актуальность при этом не утрачивается. От их решения будет во многом зависеть достоверность прогнозирования по сейсмическим данным различных геологических показателей. 13 14 Рис. 1. Результаты сейсмического моделирования по одной из скважин Шаимского нефтегазоносного региона. В настоящей статье рассматривается только один из указанных выше вопросов – каким образом проявляется структура интерференции отраженных волн в различных динамических параметрах сейсмических волн на основе изучения влияния вкладов элементарных границ и толщ непосредственно в интерференционную структуру этих динамических параметров. На начальном этапе исследований частично этот вопрос был затронут в работах [Хазиев, Трофимов, 2003; Хазиев и др., 2011]. В данной статье будет показано, каким образом продуктивные и непродуктивные интервалы изучаемого разреза отображаются в динамических параметрах волн на основе разложения волнового поля по вкладам элементарных границ и толщ в динамику сейсмической записи. В качестве модельного примера в настоящей статье взят один из результатов для одномерного сейсмического моделирования. Он получен с использованием материалов по одной из скважин Шаимского нефтегазоносного региона Западной Сибири и представлен на рис. 6 и 7 в статье [Хазиев и др., 2011]. В указанной работе дается подробное описание основных особенностей результатов моделирования, на которых, помимо прочего, приведено графическое представление эффекта интерференции сейсмической записи. В настоящей статье эти два рисунка объединены в один (рис. 1). На представленных таким образом графиках название каждого из них определяет их назначение и роль при анализе приведенных результатов сейсмомоделирования (см. рис. 1). Не останавливаясь на детальном рассмотрении этих графиков и особенностях строения анализируемого геологического разреза (их описание с необходимыми подробностями дается в [Хазиев и др., 2011]), отметим лишь следующее: отличительной особенностью рассматриваемого модельного эксперимента является применение равновременной модели с шагом квантования по времени, равным 1 мс (именно с таким шагом квантования на рассматриваемой площади Западной Сибири отрабатывались, а затем обрабатывались и интерпретировались сейсмические данные 3D-съемки МОГТ) [Трофимов и др., 2009; Хазиев и др., 2011]. Данная модель как результат аппроксимации исходных кривых акустической скорости, плотности и акустической жесткости, представленная на рис. 1, а–в, соответствует тем графикам, на которых равновременные границы ограничивают слои минимальной мощности, определяемой шагом квантования сейсмической записи по времени. Продуктивными (нефтенасыщенными) пластами в этой модели разреза являются пласты с номерами 2 и 3. Они, как отмечено в [Хазиев и др., 2011], относятся к отложениям горизонтов Т1(Ю2), Т2(Ю3+4) тюменской свиты байосс-батского возраста (J2b-bt ) средней юры. К центральной части каждого из этих пластов приурочено по одному проницаемому нефтенасыщенному пропластку. Последние имеют нефтенасыщенную толщину, равную ≈1–2 м. Остальные пласты с индексами: 1 – отложения нижнеданиловской подсвиты келловей-оксфорд-кимеридж-волжского ярусов (J3k-v) верхней юры; 4 – отложения горизонта Т3(Ю5) тюменской свиты байосс-батского возраста (J2b-bt) средней юры (с возможной нефтеносностью); 5 – отложения коры выветривания доюрского основания; 6, 7, 8, 9 и 10 – образования доюрского основания, состоящего в рассматриваемом интервале разреза из эффу- зивных, эффузивно-осадочных и метаморфизованных горных пород. Как отмечено выше, первые три графика на рис. 1, а–в – это исходные кривые акустического каротажа, распределения плотности пород, акустической жесткости (ρV) и соответствующие им равновременные модели скорости, плотности и акустической жесткости (т. е. результат аппроксимации этих исходных кривых с шагом дискретизации сейсмозаписи по времени). Зондирующим реальную геологическую среду является минимально-фазовый сейсмический импульс. Он рассмотрен совместно со своими амплитудно-частотным и фазовым спектрами ранее (в [Хазиев и др., 2011] на рис. 6, д–ж). Этот сейсмический импульс извлечен из реальных сейсмических трасс, расположенных вблизи вертикального сечения разреза, приуроченного к стволу (разрезу) рассматриваемой скважины. На следующих трех графиках рис. 1 представлены: распределение коэффициентов отражения, модельная и реальная сейсмические трассы и суммарный вклад каждой из элементарных границ (элементарных пластов) в интерференционное волновое поле (см. рис. 1, г–е). Сравнительно небольшое различие модельной и реальной сейсмических трасс, встречающееся в практике работ почти всегда при сопоставлении результатов решения прямой задачи сейсморазведки и фактических сейсмических данных, объясняется следующим: ограниченным временным интервалом анализа; использованием, как правило, некоторого приближения при аппроксимации кривых скорости, плотности и акустической жесткости; недостаточно полным учетом кратных отражений и свойств поглощающей слоистой среды; отличием рассматриваемого вертикального сечения разреза от фактически пространственного положения пути распространения продольных сейсмических волн и т. п. ИНТЕРФЕРЕНЦИОННАЯ МАТРИЦА ВКЛАДОВ Характер проявления интерференции сейсмических волн, отраженных от каждого из выделенных 10 пластов (толщ), представлен на кривых вклада каждого из этих пластов (см. рис. 1, ж). В численном виде интерференция волн приведена в “Таблице вкладов пластов”. Это практически те же кривые вклада толщ, но представленные в форме соответствующей числовой матрицы (см. рис. 1, з). Ее авторы называют “интерференционной матрицей вкладов” (ИМВ). Она является некоторым конкретным отображением процесса (механизма) формирования интерференционного волнового поля. Интерференционная матрица вкладов представляет собой прямоугольную таблицу, содержащую количество информации (вклады) об исследуемом (конкретном) параметре пласта в характеристиках волнового поля или его преобразованиях. Значение каждого элемента матрицы – это вклад рассматриваемого параметра пласта или помехи в амплитуду дискрета на данном времени (глубине). Оно получается путем расчета прямой задачи и сравнения соответствующих значений от других пластов, участвующих в формировании рассматриваемого поля, его преобразования или атрибута. В этом заключается физический и информационный смысл матрицы вкладов. Столбцы матрицы при этом представляют собой распределение вклада об изучаемом пласте по пространственной координате, а строки – соотношение количества инфор- 15 мации от разных пластов для данной точки изучаемого разреза. ИМВ достаточно полно описывает процесс формирования характеристик поля для заданной модели среды и является универсальной и в то же время удобной таблицей для исследования на количественном и качественном уровне возможностей извлечения необходимой информации из экспериментальных сейсмических данных. Ее размерность зависит от размерности используемой модели реальной среды (одномерной, двумерной, трехмерной) и от вида оператора решения прямой задачи (сверточный, лучевой, волновой и т. д.). Спектр применения ИМВ достаточно широкий: от обработки данных полевых наблюдений, решения обратной динамической задачи сейсмики, реализации интерпретационных прогнозных алгоритмов до получения конечных результатов в виде площадных карт параметров. Матрица вкладов также может быть использована для постановки и решения специальных вопросов – для сведения некорректных задач в их корректный аналог (построение регуляризирующего функционала, выбор параметров регуляризации, анализ и синтез параметров обработки, изучение слабых сигналов и т. д.). Вид ИМВ зависит от того, какая задача в данный момент решается и какую информацию нужно получить: от разбиения среды на пласты до уровня параметризации (акустические жесткости, коэффициенты отражения, коэффициент поглощения и т. д.) и т. п. Таким образом, весь процесс интерференции волн представляется поточечно (как в графическом, так и в численном видах) с шагом квантования сейсмической записи по времени. При этом хорошо видно, что каждая из амплитуд модельной сейсмической трассы содержит информацию от некоторой (вполне конкретной) совокупности вышезалегающих пластов. Как уже отмечалось выше, каждая из амплитуд сейсмической записи на каждом из ее дискретов характеризуется уникальной интерференцией вкладов от рассматриваемых пластов, отличающей ее от таковых на всех остальных дискретах сейсмической записи. Каждая из них также характеризуется различным соотношением вкладов заданных толщ и доминированием одного из них над всеми остальными. На графиках рис. 1, и, к приводятся “содержание модельной трассы” и “содержание реальной трассы”, на которых изображены помимо суммарных интерференционных сейсмических записей отнормированные локальные сейсмические записи как результат сейсмических откликов на акустические неоднородности толщ изучаемого разреза. По этим сейсмическим записям, в частности, видно, что в пределах каждой из фаз суммарной сейсмограммы, за исключением самой первой фазы, проявляется интерференция (суперпозиция) вкладов толщ. Распределение по вертикальной координате самых интенсивных значений вкладов толщ среди всех остальных, представленное на рис. 1, л, показывает, что от продуктивных пластов 2 и 3 интенсивные значения вкладов формируются только на двух сравнительно непротяженных (по сравнению с исходным расположением пластов в разрезе, см. рис. 1, м) участках сейсмотрассы. Протяженность участков сейсмотрассы, расположенных на временах t0 (1728–1734 и 1734–1742 мс соответственно), довольно небольшая, равна 6 и 8 мс. При этом указанные временные интервалы приурочены к тем участкам сейсмотрассы, которые характеризуются относительно низкими амплитудами (см. рис. 1, г). Инфор- 16 мация, представленная на рис. 1, н, показывает, что наибольшими средними значениями вклада каждого из рассматриваемых пластов в интерференционное волновое поле обладают пласты с номерами 1, 4 и 9. Продуктивные пласты 2 и 3 характеризуются некоторыми промежуточными средними значениями вклада толщ. При сейсмическом моделировании динамических характеристик волнового поля непосредственно использовался разработанный комплекс программ VKSYNT [Трофимов, Хазиев, 2011; Хазиев и др., 2011]. На его основе возможно решение следующих задач: – изучение особенностей формирования отраженных волн в исследуемом интервале разреза на основе оценки вклада элементарных границ и толщ в интерференционное волновое поле; – стратиграфическая привязка отражений; – определение временного интервала для выполнения прогноза искомых параметров выбранной системой прогнозирования, в которой используются различные параметры формы сейсмической записи; – оценка геологической информативности отражений (в том числе слабых сейсмических сигналов), соответствующих целевым интервалам разреза; – классификация имеющихся на площади работ скважин в соответствии с установленной геологической информативностью отражений и выбор числа эталонных скважин; – формирование сейсмического образа для каждой из эталонных скважин в виде совокупности динамических и кинематических характеристик, отображающих основные особенности формы сейсмической записи. ВКЛАД ГРАНИЦ И ПЛАСТОВ В РЕЗУЛЬТАТЫ ПСЕВДОАКУСТИЧЕСКИХ ПРЕОБРАЗОВАНИЙ Для получения информации о физических характеристиках пород (в частности, информации, приближающейся к акустическому и плотностному каротажу) и решения задачи расчленения геологического разреза в последнее время широко используется методика псевдоакустического каротажа (ПАК). Принципиальная особенность применения этой методики состоит в том, что осуществляется обращение сейсмической трассы в кривую акустической жесткости согласно известным формулам [Гогоненков, 1987; Боганик, Гурвич, 2006; и др.]. При этом если сейсмическая трасса Si рассматривается как последовательность коэффициентов отражения, то, имея информацию об акустической жесткости первого слоя (Vρ)0 и зная амплитуду сейсмического сигнала А, легко определяются акустические жесткости нижележащих слоев [Гогоненков, 1987]. На рис. 2, а, б представлены результаты псевдоакустических преобразований сейсмической трассы, предварительно рассмотренной на рис. 1, в двух вариантах – в виде традиционного (см. рис. 2, а) и широкополосного (см. рис. 2, б) ПАК. Из этих рисунков хорошо видны основные особенности вкладов каждого из 10 пластов, кровли которых имеют непосредственное отношение к определенным отражающим границам: на кривых вклада каждого из рассматриваемых пластов; в интерференционной матрице вкладов (ИМВ); попластовом разложении трассы ПАК в ее традиционном неотнормированном и отнормирован- Рис. 2. Оценка вклада элементарных границ и толщ в интерференционное поле псевдоакустических преобразований (ПАК) сейсмической записи: а – традиционный ПАК; б – широкополосный ПАК. ном изображениях – локальных кривых записей ПАК. При этом следует отметить две важные черты полученных результатов. Первая состоит в том, что результаты преобразования ПАК (см. рис. 2, а, б) оказываются сравнительно близкими к распределению акустической жесткости, построенному по скважинным данным, несмотря на довольно сильное “осреднение” (процедурой ПАК) “акустических деталей”, непосредственно установленных на основе использования “элементарных границ и пластов” (см. рис. 1, в). Второй важной особенностью является то, что с использованием выполненных преобразований тем не менее не удается освободиться от довольно сильной интерференции вклада рассматриваемых пластов в каждую из амплитуд трассы ПАК. Нефтеперспективные пласты с номерами 2 и 3 при этом на кривых попластового разложения почти никак не проявляются. ВКЛАД ГРАНИЦ И ПЛАСТОВ В МГНОВЕННЫЕ ДИНАМИЧЕСКИЕ ПАРАМЕТРЫ Динамические характеристики отраженных волн также сравнительно широко применяются в практике интерпретации сейсмических данных, особенно тех, которые получают в условиях сложного строения геологического разреза. При этом динамический анализ отраженных волн опирается на результаты дифференциальных динамических характеристик сейсмических записей, основанных на преобразовании Гильберта и понятии аналитического сигнала [Пудовкин, 1984; Тяпкин и др., 1986; Птецов, 1989; Боганик, Гурвич, 2006; и др.]. В этом способе непосредственно измеряются мгновенные характеристики сигналов, которым к тому же присваивается определенный физический смысл. Не останавливаясь на всех подробностях таких преобразований, отметим лишь, что комплексная функция сейсмической записи Z(t) действительного переменного, определяемая как аналитический сигнал, соответствующий “физическому” сигналу в виде действительной функции s(t), представляется в комплексной области как Z(t) = s(t) + iU(t). Здесь реальная s(t) и мнимая U(t), называемая сопряженной s(t), компоненты связаны между собой преобразованием Гильберта [Пудовкин, 1984; Тяпкин и др., 1986; Гогоненков, 1987; Птецов, 1989; Боганик, Гурвич, 2006]. По реальной компоненте, как известно, можно определить мнимую и восстановить сейсмотрассу в комплексной области. Устойчивость формального способа трансформации сигнала (преобразований Гильберта) обеспечивается при выполнении физической осуществимости “аналитического сигнала”, т. е. s(t) = 0, если t ≤ 0. Кроме этого, обязательным условием является дифференцируемость функции s(t) для всего исследуемого временного интервала (этому условию, как известно, сейсмические трассы удовлетворяют практически всегда [Тяпкин и др., 1986]). Основными мгновенными характеристиками являются следующие: 1. Мгновенная амплитуда A(t), имеющая физический смысл огибающей всех экстремумов трассы. Мгновенная амплитуда, как известно, дает возможность (с погрешностью до 5 %) количественно оценить перепад скоростей и плотностей в слоях. Интенсивность отражения при этом не зависит от фазы и частот и связывается с литологическими изменениями на границе пластов, с несогласными напласто- 18 ваниями, а также с возможными залежами углеводородов. 2. Мгновенная фаза ϕ(t) имеет физический смысл поворота вектора огибающей A(t) в комплексной плоскости при ее движении по оси времени t от начала регистрации. Она будет характеризовать абсолютное время прихода каждого отсчета – мгновенного текущего значения амплитуды сейсмического сигнала. При этом крутизна наклона мгновенной фазы или число ее сбросов в интервале времен характеризует частоту переслаивания и характер напластования [Птецов, 1989]. В то же время она не зависит от интенсивности отражения и может быть использована при выделении слабых сигналов, разрывов, сбросов, прослеживании выклиниваний [Пудовкин, 1984; Тяпкин и др., 1986]. 3. Мгновенная частота f(t) имеет физический смысл скорости вращения вектора огибающей во времени. Частоту также можно выразить через производную фазы по времени, а также через реальную и мнимую трассы. С помощью мгновенной частоты можно измерить непрерывное изменение частотного состава сейсмического сигнала как по времени, так и по горизонтали вдоль напластования. При этом появляется возможность проследить латеральные изменения литологии и нефтенасыщения в продуктивных пластах с учетом изменения свойств осадков во вмещающей толще, поскольку фаза и частота наиболее полно характеризуют характер и частоту переслаивания осадочных толщ [Птецов, 1989]. На этой же основе локализуются зоны выклинивания, приводящие к значительным изменениям частоты, выделяются зоны контактов углеводородов с пластовой водой, фиксируется смещение в сторону низких частот (“низкочастотная тень”) на отражениях от горизонтов ниже газонасыщенных пород [Пудовкин, 1984]. На рис. 3, а, б и 4, а приводятся результаты оценки вклада толщ применительно к мгновенным динамическим характеристикам отраженных волн для интервала разреза, который представлен и на рис. 1. На этих рисунках хорошо видно реализованное с помощью динамических характеристик сейсмических волн расчленение разреза в соответствии с их вышеизложенным физическим смыслом. Вместе с тем вклады каждой из 10 толщ рассматриваемого разреза в каждую из мгновенных динамических характеристик волн разнообразны и индивидуальны по своей структуре. Это хорошо проявляется на кривых вклада пластов, числовой таблице (матрице) вкладов (ИМВ) и на результатах попластового разложения трассы этих характеристик в неотнормированном и отнормированном вариантах (на локальных кривых записей мгновенных фаз, частот и амплитуд (см. рис. 3, а, б и 4, а)). Следует заметить, что по вкладу “элементарных границ” в интерференционное поле мгновенных фаз и мгновенных частот (см. рис. 3, а, б) их информативность оценивается не столь высоко по сравнению с результатами предыдущих псевдоакустических преобразований (см. рис. 2, а, б). При этом хорошо видно, что диапазон изменения вклада этих границ в интерференционное поле фаз составляет от 85 до 100 %, частот – от 88,6 до 88,7 %, тогда как на результатах псевдоакустических преобразований вклад “элементарных границ” в интерференционное поле ПАК оценивается диапазоном от 0 до 100 %. Рис. 3. Оценка вклада элементарных границ и толщ в интерференционное поле мгновенных динамических характеристик отраженных волн: а – мгновенные фазы; б – мгновенные частоты. Рис. 4. Оценка вклада элементарных границ и толщ в интерференционное поле динамических характеристик отраженных волн: а – мгновенные амплитуды; б – текущая энергия сейсмической записи. На равновременных кривых вклада “элементарных границ” в интерференционное поле мгновенных амплитуд их информативность оказывается уже значительно выше – изменения вклада этих границ оцениваются диапазоном от 5 до 55 % (см. рис. 4, а). Следует также отметить, что многие из кривых вклада пластов на мгновенных амплитудах (см. рис. 4, а) оказываются весьма близкими по своему уровню в отличие от таковых для мгновенных фаз и частот (см. рис. 3, а, б). Несмотря на вполне определенный физико-геологический смысл преобразований сейсмического волнового поля, какими являются динамические параметры (мгновенные амплитуды, фазы и частоты), тем не менее также не удается освободиться от сильной интерференции вклада рассматриваемых пластов в каждый из дискретов трассы используемых мгновенных динамических характеристик отраженных волн. Нефтеперспективные пласты с номерами 2 и 3 тоже никаким образом на кривых попластового разложения по вкладам себя не проявляют. В качестве некоторого сравнительного материала для мгновенных амплитуд (см. рис. 4, а) на рис. 4, б приведены результаты расчетов в форме текущей энергии, которая определяется как осредняющая амплитуд сейсмической трассы в скользящем окне оператора энергии заданной длины. При этом хорошо видно, что кривая текущей энергии (см. рис. 4, б) сейсмического сигнала внешне во многом повторяет кривую мгновенных амплитуд (см. рис. 4, а). Но в остальном: в структуре кривых вклада границ, вклада пластов, числовой таблице вкладов (ИМВ), в результатах попластового разложения трассы рассматриваемых характеристик в неотнормированном и отнормированном вариантах (на локальных кривых записей мгновенных фаз, частот и амплитуд) – эти различия весьма существенны (см. рис. 4, б). Кроме того, на равновременных кривых вклада “элементарных границ” в интерференционное поле текущей энергии их информативность оказывается значительной – изменения вклада этих границ оцениваются диапазоном от 0 до 100 %. ВКЛАД ГРАНИЦ И ПЛАСТОВ В РЕЗУЛЬТАТЫ ДЕКОНВОЛЮЦИИ СЕЙСМИЧЕСКОЙ ЗАПИСИ Процедура деконволюции (обратная фильтрации), позволяющая извлечь отражающие характеристики среды из сверточной модели сейсмической записи, есть, как известно, разложение наблюденного временного ряда, образованного сверткой, на его составные части. Такие процедуры давно широко используются в практике обработки сейсмических данных [Козлов, 1977; Сильвиа, Робинсон, 1983; Зенов и др., 1985; Гогоненков, 1987; Боганик, Гурвич, 2006; и др.]. При этом дополнительно может решаться целый ряд и других задач: подавление многократных отражений, волн-спутников, реверберационных волн-помех, повышение временной разрешенности записи, компенсация искажающего влияния среды, уменьшение флуктуации формы сигнала и т. д. Из-за ограниченности частотной полосы сейсмической записи и ее осложнения случайными помехами, особенно на тех составляющих, где энергия сигнала достаточно мала, “идеально” разделить сверточные компоненты практически не удается, приходится оставаться в рамках элементов структуры волнового поля. Учитывая опыт и научные интересы авторов, в настоящей статье нет необходимости перечислять все достоинства и недостатки методов обратной фильтрации (деконволюции). Этим методам посвящены многочисленные статьи и монографии [Козлов, 1977; Сильвиа, Робинсон, 1983; Зенов и др., 1985; Гогоненков, 1987; Боганик, Гурвич, 2006; и др.]. Отметим лишь то, что для практических целей используются сложные алгоритмы построения обратных фильтров со строгой геофизической и математической постановкой задачи. При этом в практике обработки деконволюция почти никогда не применяется как процедура полного сжатия сейсмического сигнала. Как справедливо отмечают авторы [Зенов и др., 1985], при наличии помех, ограниченном частотном диапазоне сигнала такая задача не может быть решена даже при известной и постоянной форме импульса. К отмеченному следует добавить и то, что деконволюция есть не что иное, как некоторая тривиальная попытка решить обратную динамическую задачу сейсмики. Как представляется, одним из существенных ее недостатков является то, что эта процедура не знает, какие частотные составляющие необходимо “вытягивать”, а какие “оставлять в покое” (в последнем случае, как правило, возникают ложные отражения). Особенность ее применения состоит и в том, что после преобразований волнового поля с помощью деконволюции, являющейся нелинейной процедурой, по преобразованному волновому полю уже практически невозможно восстановить адекватную акустическую модель реальной среды. Однако есть еще одна отличительная черта применения данной процедуры. Так, на рис. 5, а показана ситуация в целом и в частности с проблемой интерференции элементарных границ и толщ в интерференционном поле, преобразованном процедурой деконволюции. При этом хорошо видно, что деконволированная трасса стала более высокочастотной по сравнению с исходной сейсмической записью (см. рис. 1, д) и она в определенной степени повторяет поведение кривой акустической жесткости, установленной по скважинным данным (см. рис. 1, в). Информативность в виде распределения по разрезу равновременных кривых вклада элементарных границ оказывается несколько заниженной (по сравнению с таковой на исходной непреобразованной сейсмотрассе (см. рис. 1, е)), оцениваемой диапазоном их изменения от 30 до 85 %. Кривые вклада пластов в соответствии с физическим смыслом преобразований, выполненных процедурой деконволюции, оказываются более высокочастотными по сравнению с аналогичными кривыми для исходной сейсмозаписи. Они также проявляются как в числовом виде (в интерференционной матрице вкладов), так и на результатах попластового разложения деконволированной трассы в неотнормированном и отнормированном вариантах (см. рис. 5, а). И что очень важно, полученные с использованием процедуры деконволюции результаты в целом оказываются не свободными от влияния эффекта интерференции вкладов от рассматриваемых пластов в каждую из амплитуд суммарной деконволированной трассы. В колонке отображения пластов в трассе деконволюции видно, что информация от нефтеперспективного пласта 2 оказывается “раздробленной”, перекрывающейся преимущественно информацией от покрывающего пласта 1 и подстилающего пласта 3. 21 Рис. 5. Оценка вклада элементарных границ и толщ в интерференционное поле динамических характеристик сейсмической записи: а – деконволюция сейсмозаписи; б – вторая производная сейсмической записи. Информация от нефтеперспективного пласта 3 в вертикальном интервале деконволированного разреза при этом сокращается примерно в 1,5 раза по сравнению с исходным расположением этого пласта в вертикальном сечении геологического разреза. В качестве некоторого сравнительного материала для оценки результата вклада границ и пластов в интерференционную деконволированную трассу (см. рис. 5, а) на рис. 5, б дается результат расчетов в форме преобразования исходной сейсмической записи в трассу ее второй производной с перевернутой полярностью (такой вид преобразований был предложен в ОАО “ЦГЭ”). При этом хорошо видно, что кривая второй производной сейсмозаписи (см. рис. 5, б) имеет внешнее сходство с деконволированной сейсмической трассой (см. рис. 5, а). Однако на трассу второй производной по исходной сейсмограмме “накладывается” еще некоторая высокочастотная компонента, связанная с относительно высокой чувствительностью второй производной сейсмозаписи. В остальном – в структуре кривых вклада границ, вклада пластов, числовой таблице вкладов (ИМВ), в результатах попластового разложения трассы рассматриваемых характеристик в неотнормированном и отнормированном вариантах (на локальных кривых записей второй производной) – эти различия с аналогичными результатами деконволюции оказываются существенными (см. рис. 5, б). На равновременных кривых вклада “элементарных границ” в интерференционное поле второй производной их информативность оказывается несколько выше, чем на результатах деконволюции, – изменения вклада этих границ здесь оцениваются диапазоном от 0 до 80 %. Основные выводы по выполненным исследованиям сводятся к следующему. 1. Без учета вклада элементарных границ и толщ в интерференционное волновое поле, а также в различные динамические параметры отраженных волн весьма сложно интерпретировать акустические неоднородности разреза, изучаемые только на основе элементов структуры волнового поля. Без вышеотмеченных компонент поля и его динамических параметров (вкладов элементарных границ и толщ) сложно определить место отображения конкретных целевых интервалов на временном разрезе, связанных с продуктивными или потенциально продуктивными интервалами геологического разреза. 2. В условиях, когда при интерпретации сейсмических данных (особенно при прогнозировании по сейсмическим данным различных геологических показателей) приходится работать с интерференционными сейсмическими записями и их динамическими характеристиками, следует предварительно оценить вклады элементарных границ и пластов в поле динамических параметров. Правильный выбор целевого временного интервала, в котором находится максимально возможная информация (вклад) от целевого объекта, позволит существенно повысить эффективность прогнозирования. 3. Идеальным способом учета (исключения) эффекта интерференции волн и построения тонкослоистых моделей реальной среды является численное решение обратной динамической задачи сейсмики, позволяющее разделить информацию, содержащуюся в сейсмической записи, на две: об источнике возбуждения упругих колебаний и о реальной геологической среде [Хазиев, Трофимов, 2003; Милашин и др., 2004; Трофимов и др., 2007, 2009; Трофимов, Хазиев, 2011; Хазиев и др., 2011; и др.]. Таким образом, в процессе интерпретации сейсмических данных, особенно при использовании динамических параметров отраженных волн с целью повышения эффективности прогноза акустических неоднородностей, состава и свойств геологического разреза, целесообразно выполнять детальную оценку вклада в интерференционное волновое поле и динамические характеристики отраженных волн. Литература Боганик Г.Н., Гурвич И.И. Сейсморазведка. М.: АИС, 2006. 744 с. Гогоненков Г.Н. Изучение детального строения осадочных толщ сейсморазведкой. М.: Недра, 1987. 221 с. Зенов А.А., Малкин А.Л., Сорин А.Я., Фиников Д.Б. Современные методы обратной и корректирующей фильтрации сейсмических записей. М.: ВНИИОЭНГ. Обзорная информация. Серия нефтегазовая геология и геофизика, 1985, 60 с. Козлов Е.А. Прогностическая фильтрация кратных волн в неидеальных условиях // Прикладная геофизика. 1977. № 87. С. 3–19. Милашин В.А., Трофимов В.Л., Хазиев Ф.Ф. Выделение слабых сигналов методом сейсмической инверсии // Материалы 7-й науч.-практ. конф. “Пути реализации нефтегазового потенциала ХМАО”. Ханты-Мансийск, 2004. Т. 2. С. 295–307. Птецов С.Н. Анализ волновых полей для прогнозирования геологического разреза. М.: Недра, 1989. 135 с. Пудовкин А.А. Алгоритмическое и методическое обеспечение литологического расчленения отложений по динамическим характеристикам отраженных волн в методе многократных перекрытий. Разведочная геофизика. М.: Обзор ВИЭМС, 1984. 65 с. Сильвиа М.Т., Робинсон Э.А. Обратная фильтрация геофизических временных рядов при разведке на нефть и газ. М.: Недра, 1983. 247 с. Трофимов В.Л., Хазиев Ф.Ф., Милашин В.А., Качкин А.А., Тимонин А.Б., Мальцев Г.А. Автоматизированная обработка и интерпретация данных ГИС для обнаружения нефтеперспективных объектов методами высокоразрешающей сейсмики // Технологии сейсморазведки. 2007. № 2. С. 54–66. Трофимов В.Л., Милашин В.А., Хазиев Ф.Ф., Черников Д.И., Качкин А.А., Тимонин А.Б. Специальная обработка и интерпретация данных сейсмических наблюдений в сложных геологических условиях методом высокоразрешающей сейсмики // Технологии сейсморазведки. 2009. № 3. С. 36–50. Трофимов В.Л., Хазиев Ф.Ф. Изучение влияния состава и свойств пород на геолого-геофизические параметры нефтеперспективных отложений // Технологии сейсморазведки. 2011. № 1. С. 22–33. Тяпкин Ю.К., Бельфер И.К., Погожев В.М., Мушин И.А., Митрофанов Г.М. Оценка возможностей использования мгновенных динамических характеристик сейсмических записей при поисках нефти и газа. Разведочная геофизика. М.: Обзор ВИЭМС, 1986. 76 с. Хазиев Ф.Ф., Трофимов В.Л. Модельные исследования результатов решения обратной динамической задачи сейсмики // Геофизика. Технологии сейсморазведки. 2003. С. 27–37. Хазиев Ф.Ф., Трофимов В.Л., Милашин В.А. Оценка вклада элементарных границ и толщ в сейсмическое волновое поле для многослойных поглощающих сред // Технологии сейсморазведки. 2011. № 2. С. 86–96. 23 КОРОТКО ОБ АВТОРАХ ТРОФИМОВ Владимир Леонидович – кандидат геолого-минералогических наук, руководитель департамента интерпретации ООО “Мегацентр-Плюс”. Тел.: 8(499) 192-63-65 E-mail: trofimvl@gmail.com ХАЗИЕВ Фаниль Фаязович – ведущий геофизик ООО “Мегацентр-Плюс”. Тел.: 8(499) 192-63-65 E-mail: hrsgeo@gmail.ru МИЛАШИН Владимир Алексеевич – кандидат геолого-минералогических наук, генеральный директор ООО “Мегацентр-Плюс”. Тел.: 8(499) 192-63-65 E-mail: milashin@pentr.msk.ru 24