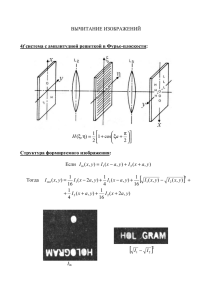
Рекурсия. Примеры классических задач Задача 1. Вычислить
реклама

Рекурсия. Примеры классических задач
Задача 1. Вычислить факториал числа N.
Для решения задачи рекурсивным алгоритмом необходимо знать рекуррентное правило
вычисления факториала и условие выхода из рекурсии.
N!=(N−1)! ∗ N, если N = 0, то N! = 1
//Классический способ
#include <iostream>;
#include<cmath>;
#include<fstream>;
using namespace std;
int main()
{
ifstream in;
ofstream out;
in.open("input.txt");
out.open("output.txt");
long long int n, p=1;
cin>>n;
for (int i=1; i<=n; i++)
{
p=p*i;
}
cout<<p;
in.close();
out.close();
return 0;
}
//Решение при помощи рекурсии
#include <iostream>;
#include<cmath>;
#include<fstream>;
using namespace std;
// описание рекурсивной функции
long long int fact(int k)
{
if (k==1) return 1;
else
return k*fact(k-1);
}
int main()
{
ifstream in;
ofstream out;
in.open("input.txt");
out.open("output.txt");
long long int n;
in>>n;
out<<fact(n); // Вызов
рекурсии
in.close();
out.close();
return 0;
}
Задача 2. По заданному числу N вычислить число Фибоначчи F(N)
Для решения задачи необходимо знать, что последовательностью Фибоначчи называется
последовательность чисел F0, F1, ..., Fn, ..., где
F0 = 0, F1 = 1, Fk = Fk-1 + Fk-2 (k > 1)
//Классический способ. Динамическое
программирование. Псевдокод
//Решение при помощи рекурсии.
Псевдокод процедуры
создать массив F[0...n]
F[0]←0,F[1]←1
для i от 1 до n:
F[i]← F[i−1] +F[i−2]
вернуть F[n]
Рисунок рекурсивных
вызовов для задачи
«Вычисление чисел
Фибоначчи» входит в
состав курса «Алгоритмы и
структуры данных»
https://stepic.org/lesson
Fib1 (n)
Если n ≤ 1 :
вернуть n
Вернуть Fib1(n−1) +Fib1(n−2)