4. В соответствии со значениями многомерной средней

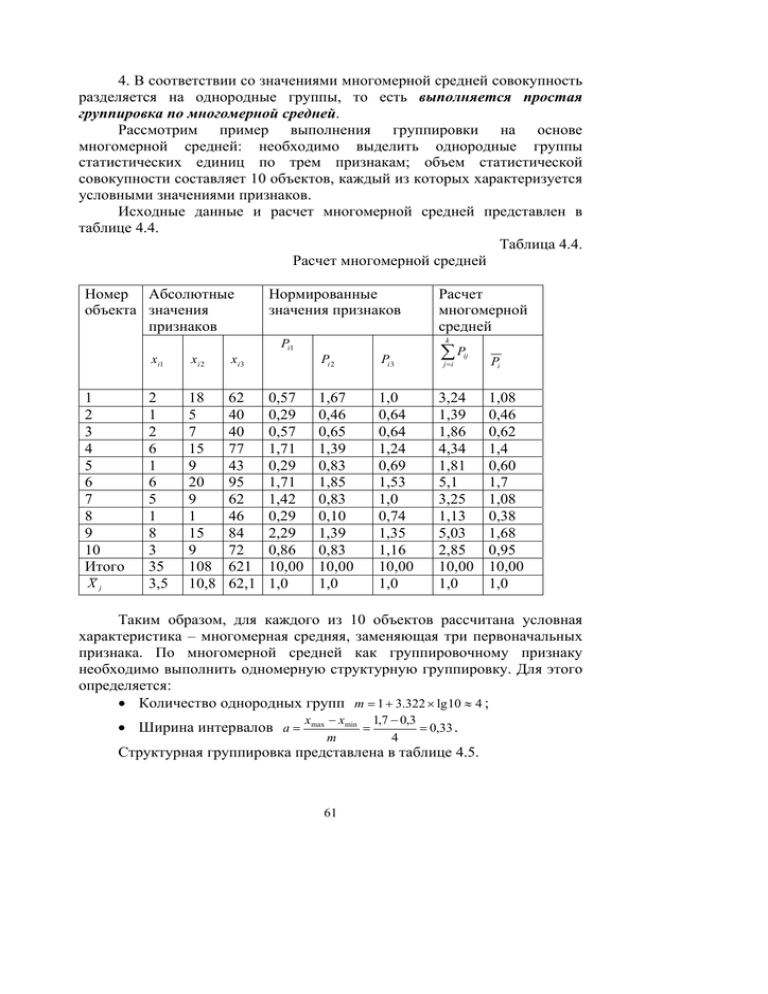
4. В соответствии со значениями многомерной средней совокупность
разделяется на однородные группы, то есть выполняется простая
группировка по многомерной средней.
Рассмотрим пример выполнения группировки на основе
многомерной средней: необходимо выделить однородные группы
статистических единиц по трем признакам; объем статистической
совокупности составляет 10 объектов, каждый из которых характеризуется
условными значениями признаков.
Исходные данные и расчет многомерной средней представлен в
таблице 4.4.
Таблица 4.4.
Расчет многомерной средней
Номер Абсолютные
объекта значения
признаков
Нормированные
значения признаков
Pi1
1
2
3
4
5
6
7
8
9
10
Итого
Xj
xi1
xi 2
xi 3
2
1
2
6
1
6
5
1
8
3
35
3,5
18
5
7
15
9
20
9
1
15
9
108
10,8
62
40
40
77
43
95
62
46
84
72
621
62,1
0,57
0,29
0,57
1,71
0,29
1,71
1,42
0,29
2,29
0,86
10,00
1,0
Расчет
многомерной
средней
k
Pi 2
Pi 3
∑P
1,67
0,46
0,65
1,39
0,83
1,85
0,83
0,10
1,39
0,83
10,00
1,0
1,0
0,64
0,64
1,24
0,69
1,53
1,0
0,74
1,35
1,16
10,00
1,0
3,24
1,39
1,86
4,34
1,81
5,1
3,25
1,13
5,03
2,85
10,00
1,0
j =i
ij
Pi
1,08
0,46
0,62
1,4
0,60
1,7
1,08
0,38
1,68
0,95
10,00
1,0
Таким образом, для каждого из 10 объектов рассчитана условная
характеристика – многомерная средняя, заменяющая три первоначальных
признака. По многомерной средней как группировочному признаку
необходимо выполнить одномерную структурную группировку. Для этого
определяется:
• Количество однородных групп m = 1 + 3.322 × lg 10 ≈ 4 ;
• Ширина интервалов a =
xmax − xmin 1,7 − 0,3
=
= 0,33 .
m
4
Структурная группировка представлена в таблице 4.5.
61
Таблица 4.5.
Группировка объектов по многомерной средней
№
групп
1
2
3
4
Итого
Параметры групп
xiн
xiв
ai
0,38
0,71 0,33
0,71
1,04 0,33
1,04
1,37 0,33
1,37
1,07 0,33
0,38
1,07 1,32
Номера объектов
Количество объектов
в группе, ni
2,3,5,8
10
1,7
4,6,9
-
4
1
2
3
10
Таким образом, 10 объектов были распределены по 4-м однородным
группам.
При втором подходе к выполнению многомерных группировок
каждая единица совокупности, обладающая набором из k признаков
рассматривается как точка в k-мерном пространстве – пространстве
признаков, а каждому признаку придается смысл координаты. Задача
классификации в этом случае сводится к выделению сгущений объектов в
этом пространстве. Для этого используются различные алгоритмы, но
всегда однородные группы выделяются на основании близости объектов
по совокупности признаков. Мерой близости объектов, то есть мерой
сходства единиц совокупности, могут служить различные критерии.
Выделяют три типа мер сходства:
•
Коэффициенты подобия;
•
коэффициенты связи;
•
показатели расстояния.
Коэффициенты подобия используются для измерения степени
близости между парой объектов, каждый из признаков которых принимает
значения 0 или 1.
Наиболее простой коэффициент подобия рассчитывается по
формуле:
S ij =
Pij
m
;
где Pij - число совпадений признаков у объектов i и j;
m – общее число признаков, по которым осуществляется сравнение.
0 ≤ S ij ≤ 1 .
Коэффициенты корреляции используются как измерители силы
связи между статистическими единицами или между признаками. Для
измерения тесноты связи количественных признаков применяют
коэффициенты линейной корреляции.
В кластерном анализе мерой сходства является мера расстояния
между двумя объектами I и
j. Для количественных признаков
используется Евклидово расстояние:
62