Лекция 18 Волны. Акустика

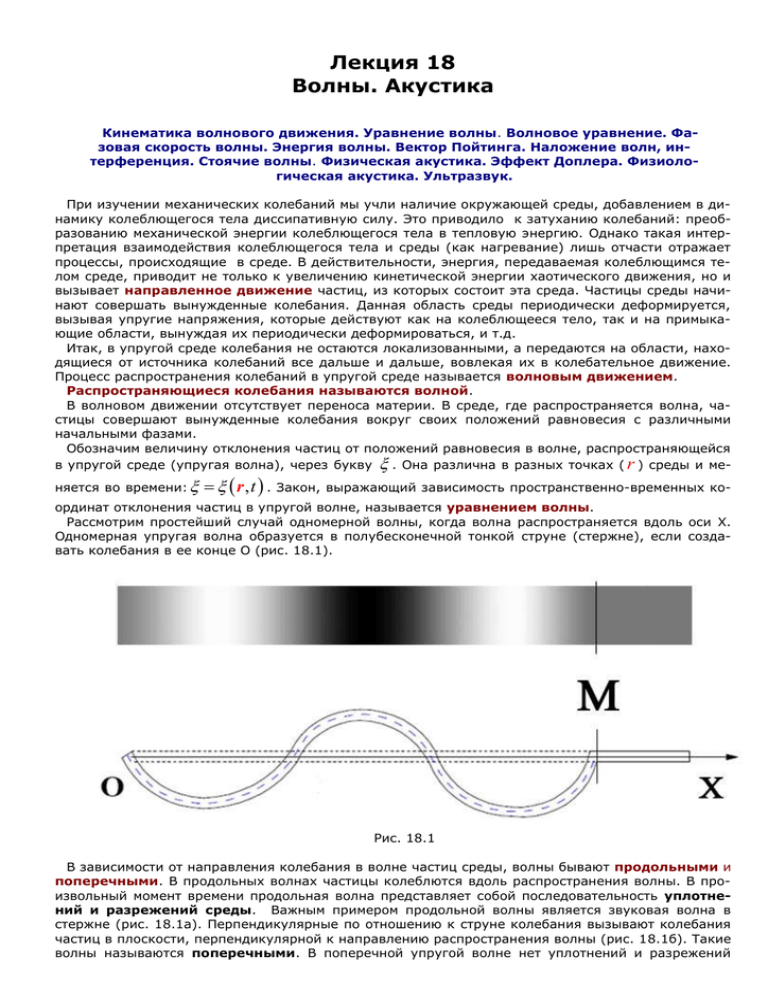
Лекция 18
Волны. Акустика
Кинематика волнового движения. Уравнение волны. Волновое уравнение. Фазовая скорость волны. Энергия волны. Вектор Пойтинга. Наложение волн, интерференция. Стоячие волны. Физическая акустика. Эффект Доплера. Физиологическая акустика. Ультразвук.
При изучении механических колебаний мы учли наличие окружающей среды, добавлением в динамику колеблющегося тела диссипативную силу. Это приводило к затуханию колебаний: преобразованию механической энергии колеблющегося тела в тепловую энергию. Однако такая интерпретация взаимодействия колеблющегося тела и среды (как нагревание) лишь отчасти отражает
процессы, происходящие в среде. В действительности, энергия, передаваемая колеблющимся телом среде, приводит не только к увеличению кинетической энергии хаотического движения, но и
вызывает направленное движение частиц, из которых состоит эта среда. Частицы среды начинают совершать вынужденные колебания. Данная область среды периодически деформируется,
вызывая упругие напряжения, которые действуют как на колеблющееся тело, так и на примыкающие области, вынуждая их периодически деформироваться, и т.д.
Итак, в упругой среде колебания не остаются локализованными, а передаются на области, находящиеся от источника колебаний все дальше и дальше, вовлекая их в колебательное движение.
Процесс распространения колебаний в упругой среде называется волновым движением.
Распространяющиеся колебания называются волной.
В волновом движении отсутствует переноса материи. В среде, где распространяется волна, частицы совершают вынужденные колебания вокруг своих положений равновесия с различными
начальными фазами.
Обозначим величину отклонения частиц от положений равновесия в волне, распространяющейся
в упругой среде (упругая волна), через букву  . Она различна в разных точках ( r ) среды и меняется во времени: 
   r ,t  . Закон, выражающий зависимость пространственно-временных ко-
ординат отклонения частиц в упругой волне, называется уравнением волны.
Рассмотрим простейший случай одномерной волны, когда волна распространяется вдоль оси X.
Одномерная упругая волна образуется в полубесконечной тонкой струне (стержне), если создавать колебания в ее конце О (рис. 18.1).
Рис. 18.1
В зависимости от направления колебания в волне частиц среды, волны бывают продольными и
поперечными. В продольных волнах частицы колеблются вдоль распространения волны. В произвольный момент времени продольная волна представляет собой последовательность уплотнений и разрежений среды. Важным примером продольной волны является звуковая волна в
стержне (рис. 18.1а). Перпендикулярные по отношению к струне колебания вызывают колебания
частиц в плоскости, перпендикулярной к направлению распространения волны (рис. 18.1б). Такие
волны называются поперечными. В поперечной упругой волне нет уплотнений и разрежений
среды, то есть отсутствуют деформации сжатия и растяжения. Здесь мы имеем дело с деформациями скольжения.
Существуют волновые движения, содержащие в себе компоненты и продольных, и поперечных
колебаний, то есть они и не продольны, и не поперечны. Например, в возникающих на поверхности воды, так называемых, гравитационных волнах частицы совершают вертикальные движения по окружности с радиусом, убывающим с глубиной. анимация
Как и любое колебание, волны можно представлять в виде наложения гармонических (меняющихся по закону синуса или косинуса) волн с различными параметрами. Ограничимся, поэтому,
исследованием гармонических волн.
Пусть в токе О струне (стержню) переданы колебания
  0, t   A sin t    ,
(18.1)
которые распространяются вдоль нее со скоростью u. Скорость распространения возбуждений u,
которая называется скоростью волны, не следует путать со скоростью колебательного движения
частицы в волне
v   t .
Через определенное время
t1  x / u
возбужденные в точке О коле-
бания достигнут точки М стержня (рис. 11.1). Следовательно, если потери энергии при распространении отсутствуют, то колебания в точке М будут иметь ту же частоту  и амплитуду А, но
будут «отставать» от колебаний в точке О на время
t1 :


  x, t   A sin   t  t1      A sin t 
x

  .
u

(18.2)
В отличие от колебаний волны наделены как временной, так и пространственной периодичностью. Период T волны в произвольной точке среды x это период колебаний частицы в
этой точке:
  x, t  T     x, t  ,
откуда
T  2   1 
.
(18.3)
Циклическая  и линейная  частоты колебания частицы в волне называются соответственными частотами волны. Расстояние между ближайшими точками, колеблющимися в одинаковой фазе
в данный момент времени, называется длиной волны λ, которая и представляет величину пространственного периода волны:
  x   , t     x, t  ,
откуда
 u  2 ,
или
  u /  uT .
(18.4)
Значит, длина волны это расстояние, которое проходит волна за один период колебаний.
Учитывая полученные соотношения, уравнение одномерной гармонической волны (18.2)
запишем в виде


1 x
   ,
T  

  x, t   A sin  2 

или
  x, t   Asin t  kx    ,
(18.5')
(18.5)
где
k  2 
(18.6)
называется волновым числом (количество волн, умещающихся в
Величина
2
см).
  x, t   t  kx  
(18.7)
в уравнении волны (18.5) называется фазой волны, а   x,0  – есть начальная фаза колебаний в данной точке x . Значит, колебания в точках x1 и x 2 отличаются только начальными фазами:
  k  x1  x2  .
Если эта разность равна
2 n , n  1, 2 ,
т.е. эти точки находятся друг от друга на расстоя-
нии, кратном  , то они совершают одинаковые движения.
Геометрическое место тех точек, в которых в данный момент времени частицы имеют одинаковую фазу, называется волновой поверхностью или волновым фронтом. По виду волнового
фронта волны подразделяются на плоские, цилиндрические, сферические и другие. Например, одномерная гармоническая волна (18.5) – плоская волна, так как при   const получаем
x
t    
k
 const ,
которая есть уравнение плоскости, проходящей через точку x , перпендикулярно распространения волны.
Сферическую волну можно получить, возбудив гармонические колебания в какой-либо точке
бесконечной среды. Уравнением сферической волны является
  r, t  
A
sin t  kr    , r  0,
r
где r – расстояние рассматриваемой точки от источника волны. Заметим, что амплитуда сферической волны убывает даже в случае отсутствия поглощения. Это следует из закона сохранения
энергии.
Дифференцируя фазу волны (18.7), считая ее постоянной, получим  dt  kdx  0 , откуда
dx 
  u.
dt k
Значит,
волны.
u
(18.8)
– скорость распространения фронта волны, которая называется фазовой скоростью
Волновое уравнение. Фазовая скорость волны.
Обсудим динамику волн в стержне, рассмотренных в предыдущем параграфе. Пусть, в стержне
распространяется поперечная волна. Мысленно выделим в стержне цилиндрический элемент длиной x , находящийся на расстоянии x от его левого конца (рис. 18.2). Если обозначить в волновом поле смещение основания цилиндра с координатой
смещение
x
в момент времени
t
через
  x, t  , то
Рис. 18.2
основания
x x
будет
  x  x, t  . В зависимости от разности этих величин рассматриваемый
цилиндрический элемент будет подвергаться деформации сжатия или растяжения (зависимость
  x, t 
- нелинейная). Определим относительное удлинение цилиндрического элемента

Преобразовав
  x  x, t 
   x  x, t     x, t 

x
x
в ряд по степеням

x , и считая x
(18.9´)
очень маленьким, будем иметь
  x, t 
.
x
(18.9)
Согласно закону Гука, в стержне возникнет нормальное напряжение
  E  E
где
E

,
x
(18.10)
– модуль Юнга материала стержня.
x и можно взять ускорение элементарного цилиндра
 1, так что из (18.9´) 

, а массу – m   x , где  – плотность стержня,  – площадь продольного се2
Обычно
2
равным
t
чения. Для применения второго закона Ньютона к рассматриваемому элементарному цилиндру
определим равнодействующую нормальных сил, действующих на него в данный момент времени:

 2
F     x  x     x   t  
 x  E 2  x,
x
x
(18.11)
где для получения последнего выражения использован закон Гука (18.10).
Второй закон Ньютона дает
 2
 2
x 2  E x 2 ,
x
x
откуда
 2  x, t    2  x, t 
 
 0.
x 2
E
t 2
(18.12)
Полученное дифференциальное уравнение и есть волновое уравнение. Его общее решение
имеет вид
  x, t   f1  x  ut   f 2  x  ut  ,
где
f1
и
f2
(18.13)
– произвольные функции, а
u E 
(18.14)
- скорость продольной упругой волны.
Первый член общего решения волнового уравнения описывает волну, распространяющуюся по
положительному направлению оси X, а второй член – в противоположном направлении. Задав
начальные и краевые условия, мы конкретизируем вид решения (18.12). В примере полубесконечной струны (стержня) из начального условия (18.1) получаем
f2  0 , а
f1  x  vt   A sin t  kx    .
То, что скорость продольных волн в упругой среде зависит от модуля Юнга, вполне понятно, так
как распространение продольных волн сопровождается деформациями сжатия и растяжения среды. Подобным же образом можно показать, что скорость упругой поперечной волны дается
формулой
v G ,
(18.15)
где G – модуль сдвига среды, так как распространение поперечных упругих волн связано с
деформациями сдвига. Жидкости и газы лишены упругих свойств, связанных с деформациями
сдвига. По этой причине поперечные упругие волны в жидкостях и газах распространяться
не могут.
Энергия волны. Вектор Пойтинга.
Источник волн, деформируя примыкающие к нему объемы, непрерывно передает им энергию,
которая перемещает волну в среде.
Определим изменение энергии объема dV упругого стержня, обусловленного распространением
в нем плоской продольной волны
  x, t   A sin t  kx    .
(18.16)
В качестве объема dV выберем выделенный в предыдущем параграфе элементарный цилиндр.
Кинетическая энергия, приобретенная им в волновом поле, будет равна
v2
2
A 2 2
dK   dV  dm  
dx cos 2 t  kx    .
2
2
2
(18.17)
Изменение потенциальной энергии равно упругой энергии, обусловленной относительной деформацией ε элементарного цилиндра
1
dU  E 2 dx
2
С другой стороны, пользуясь выражениями (18.5), (18.9) и
 2  A2 k 2 cos 2 t  kx    
(18.18)
v   t , получим
k 2v2
2

v2
v2


,
u2
E
(18.19)
где для получения двух последних выражений мы воспользовались формулами (18.8) и (18.14).
Подставляя (18.19) в (18.18) будем иметь
1
dU  dT   v 2 dV .
2
(18.20)
Это свойство характерно для любой одномерной бегущей волны.
Изменение полной механической энергии рассматриваемого элементарного объема будет
dE  dT  dU   v 2   A2 2 dV cos2 t  kx    .
Отсюда для плотности энергии плоской синусоидальной волны будем иметь
w
dE
  v 2   A2 2 cos 2 t  kx   
dV
.
(18.21)
Значит, кинетическая и потенциальная энергия волнового движения - периодические функции
от
x, t . Они колеблются в одинаковой фазе с одинаковыми амплитудами, равными  A2 2 / 2 . Эти
закономерности верны для любой упругой волны независимо от вида волнового фронта и деформации, так как они обусловлены механизмом распространения упругой волны. Очень важно, что
полная механическая энергия волнового движения в любом объеме dV периодически меняется
во времени. Это и есть основное энергетическое различие колебательных и волновых движений,
поскольку в первом полная энергия постоянна (изменения кинетической и потенциальной энергий
происходят в противоположных фазах). Распространение волны в упругой среде неразрывно связано с процессом передачи энергии от одних участков среды к другим. Именно поэтому при волновом движении объемная плотность энергии периодически меняется со временем в каждой точке
среды.
Волна переносит энергию. Скорость распространения энергии в волне равна скорости той поверхности, на которой плотность энергии имеет наибольшее значение. В плоской гармонической
волне, как следует из формулы
A2 2
w   A  cos t  kx     
1  cos 2 t  kx     ,
2
поверхность, на которой обьемная плотность энергии волны максимальна - w  wmax , определяется условием t  kx    0 , откуда следует, что скорость распространения этой поверхности
совпадает с фазовой скоростью волны u   / k . Скорость переноса энергии, которая называ2
2
2
ется групповой скоростью волны, в общем случае не совпадает е ее фазовой скоростью.
Перенос энергии волной характеризуется вектором Пойтинга или вектором плотности потока энергии. Это - энергия, переносимая за единицу времени через единичную площадку, перпендикулярную направлению распространения волны:

dEuˆ
,
dtd  cos 
где dE – энергия, перенесенная через площадь d за время
гии, заключенной в заштрихованной области (рис. 18.3):
dE  wvdtd  cos .
(19.22)
dt . Понятно, что она равна энер-
Рис. 18.3
Учитывая последнее выражение в определении вектора Пойтинга, получим
  wuгр .
(18.23)
Значит, вектор Пойтинга – это произведение плотности энергии волны и групповой
скорости ее распространения.
Наложение волн
Рассмотрим наложение двух волн с одинаковой длиной волны в однородной и изотропной среде.
Предположим, что эти волны возбуждаются одновременно источниками, расположенными в точках
O1
и
O2
(рис. 18.4). В произвольной точке среды М будем иметь
Рис.18.4
A1
A
sin 1t  k1 x  1   1 sin 1
r1
r1
A
A
 2  2 sin 2 t  k2 x  2   2 sin  2
r2
r2
1 
(18.24)
(18.25)
Согласно принципу наложения колебаний в точке М получим новое гармоническое колебание:
  1   2  A sin ,
где
(18.26)
2
2
A  A 
AA
A   1    2   2 1 2 cos  1   2  ,
r1r2
 r1   r2 
A
 A

A
A
tg    1 sin 1  2 sin  2   1 cos 1  2 cos  2 
r2
r2
 r1
  r1

2
(18.27)
(18.28)
Результат наложения волн зависит от среднего значения последнего члена в выражении квадрата амплитуды (18.27) результирующей волны (18.26). Пространственно-временная зависимость
этого члена, или как его еще называют, интерференционного члена, обусловлена разностью
фаз накладывающихся волн:
1   2  2  1  t  k  r2  r1   2  1  .
Отсюда следует, что временная зависимость разности фаз исчезает, если накладывающиеся
волны имеют одинаковую частоту:
1  2 .
Волны, разность фаз которых не зависит от времени, называются когерентными.
При наложении когерентных волн возникает явление интерференции – периодическое
распределение энергии между волнами в пространстве. Действительно, для когерентных волн выражение (18.26) имеет следующий вид:
2
2
A  A 
AA
 2

A   1    2   2 1 2 cos   r2  r1   2  1   ,
r1r2


 r1   r2 
2
(18.29)
откуда следует, что в точке М амплитуда результирующего колебания будет максимальной, если
2

Отсюда, если
r
2
 r1   2  1   2 n; n  0, 1, 2,...
1   2 , то для разности хода волн (ход волны
– это путь, проходимый волной от
источника до рассматриваемой точки) будем иметь
r2  r1  n .
(18.30’)
Если разность хода равна целому числу длин волн, то волны усиливают друг друга, и
мы имеем максимальную интенсивность. Если же
r2  r1   2n  1  2,
(18.30)
то будем иметь минимум интенсивности.
При наложении некогерентных волн явление интерференции не наблюдается, так как среднее
квадрата результирующей амплитуды равна сумме квадратов средних амплитуд накладывающихся волн.
Стоячие волны
Следствием интерференции является образование стоячих волн. Простейшую одномерную стоячую волну можно возбудить, вызвав гармонические колебания на одном из концов
стержня (или гибкой струны) конечной длины . В зависимости от способа возбуждения колебаний, бегущая волна
1  x, t   A0 sin t  kx  ,
(18.31)
может быть или продольной, или поперечной. Отражаясь от другого конца стержня (струны), в
той же точке М волна создаст колебания по закону (здесь поглощение волны игнорируется)
Рис.18.5
2  x, t   A0 sin t  k  x  2     ,
где

(18.32)
– возможное изменение фазы волны из-за отражения. По принципу наложения волн ре-
зультирующее колебание в точке М будет
  x, t   2 A0 cos k   x    2  sin t  k   2 .
(18.33)
Полученное выражение есть уравнение одномерной стоячей волны, где
A x   2 A0 cos k   x    2 .
(18.34)
Периодическая функция, зависящая от координат и представляющая амплитуду стоячей волны.
Заметим, что в точках
k   x    2   n; n  0, 1, 2,...
амплитуда колебаний максимальна и равна
2 A0 .
(18.35)
Эти точки называются пучностями стоячей
волны. А точки, определяемые условием
k   x    2   2n  1 2; n  0, 1, 2,...
характеризуются нулевым значением амплитуды и называются узлами стоячей волны.
рис. 18.6 a
(18.36)
рис. 18.6 б
Во время отражения упругих волн изменение фазы продольной волны

зависит величины
волнового сопротивления сред по разные стороны от поверхности отражения. Под волновым
сопротивлением упругой среды понимают произведение  u , где  – плотность массы среды, а
u
– фазовая скорость распространения продольной волны. Если продольная волна из среды с
волновым сопротивлением
1u1
падает на границу среды с волновым сопротивлением
 2 u2
по
направлению нормали, то
  0, если 2u2  1u1 ,
   , если 2u2  1u1 .
(18.37)
Расстояние между двумя пучностями (узлами) называется длиной стоячей волны:
ст  x2  x1 

k


2
.
(18.38)
Значит, длина стоячей волны равна половине длине соответствующей бегущей волны (рис. 18.6
а).
Заметим одну важную особенность стоячей волны.
Все точки в области между узлами стоячей волны колеблются в одинаковой фазе, но с
разными амплитудами (рис. 18.6 а). Действительно, в уравнении стоячей волны (18.33) зависящий от времени фазовый член не зависит от координаты. При переходе от одной ячейки стоячей
волны к другой амплитудный член (18.34) меняет знак. Это означает, что в соседних ячейках
колебания совершаются в противоположных фазах.
В отличие от бегущей волны, в стоячей волне отсутствует перенос энергии. В каждой из
ячеек полная энергия не меняется с течением времени, а только периодически переходит из кинетической энергии в потенциальную и наоборот. Это является следствием того, что стоячая волна представляет собой наложение противоположно двигающихся бегущих волн, переносящих
одинаковую энергию. В этом и есть причина того, что они получили название стоячих волн.
Во время свободных колебаний закрепленной за один конец упругой струны в ней устанавливаются стоячие волны, причем на закрепленном конце мы будем иметь узел, а на открытом конце –
пучность (рис. 18.6 б). Следовательно, в такой струне должно поместиться четное число полуволн:
  2m  1 ст 2, m  1;2;...
Если закреплены оба конца струны (например, в струнных музыкальных инструментах), то на
обоих концах струны будем иметь узлы. Это означает, что в струне должно помещаться целое
число длин волн
Но
 mст
ст   / 2  u / 2 . Так что

u
m, m  1;2;...
2
(18.39)
которая представляет спектр частот собственных колебаний струны. Нетрудно показать,
что собственная частота струны зависит от напряжения растяжения σ. Оно выражается зависимостью скорости распространения волн вдоль натянутой струны
u  .
Этим и обусловлена «настройка» струнных инструментов – увеличением или уменьшением силы
натяжения в них струн.
Акустика.
Так называется учение о звуке. Причиной звуковых ощущений людей и животных является воздействие на их органы слуха упругих звуковых волн, распространяющихся в воздухе от источника
звука. Человек с нормальным слухом способен воспринимать в форме звука такие упругие волны,
частоты которых не меньше 16 Гц и не больше 20 кГц. Звуковые волны с частотами, меньшими 16
Гц, называют инфразвуком, а волны с частотами, большими 20 кГц, - ультразвуком. Человеческое ухо наиболее чувствительно к волнам в области частот 1,5-3 кГц.
Рассматривая любое акустическое явление, следует учесть, что с одной стороны, звук – это
физический процесс распространения упругих волн в среде, а с другой - психофизиологический процесс восприятия указанного физического процесса. Первый круг вопросов
является предметом исследования физической акустики, а второй - физиологической акустики.
Физические характеристики звука.
Для характеристики звука в акустике используются частота звуковой волны (или спектр частот,
для сложного звука) и интенсивность звука.
Интенсивностью, или силой, звука называется модуль среднего значения вектора плотности
потока (вектора Умова-Пойтинга) энергии звуковой волны
I  w  u,
где u – групповая скорость волны.
Для синусоидальной волны скорость
мулой
где
A
– амплитуда волны,

u
совпадает с фазовой скоростью, а w выражается фор-
w  12  A2 2 ,
– плотность массы упругой среды.
Следовательно, для интенсивности синусоидальной звуковой волны получаем
I  12 A2 2  u.
В системе единиц СИ интенсивность звука измеряется в единицах Вт / м .
Давление среды, в которой распространяется звуковая волна, в каждой точке непрерывно колеблется. Изменение давления среды  в звуковой волне называется звуковым давлением,
2
которое равно произведению волнового сопротивления среды
 u на скорость v
частиц в волне:
p   uv .
Средняя величина квадрата звукового давления связана с интенсивностью синусоидальной звуковой волны простой формулой
(p)2  uI , или
Здесь
p3
pз  (p)2  uI .
называется среднеквадратичным звуковым давлением.
В воздухе при нормальном давлении и температуре
200 C ( u  418 кг / м с )
2
значения интен-
сивности и среднеквадратичного давления для различных звуков приведены в таблице.
Таблица интенсивностей и среднеквадратичного давления различных звуков
Звук
Расстояние от
источника в
м
Тихий разговор
Громкий разговор
Фортиссимо оркестра
Шум самолета
Интенсивность
звука в
Вт / м
Среднеквадратичное дав-
2
ление в
2  103
0,06  0,2
108
105  104
102
1
1
10
5
Н / м2
2
20
1
Эффект Доплера.
Регистрируемая частота звука ν совпадает с частотой колебаний источника
0
лишь в том слу-
чае, когда приемник и источник неподвижны относительно среды. В остальных случаях
 0 .
Например, если источник приближается к неподвижному наблюдателю, то звуковой сигнал кажется более высоким, а при удалении от наблюдателя – более низким, чем тон неподвижного источника. Это явление называется эффектом Доплера. анимация
Распространение звука в упругой среде связано с колебаниями давления и плотности в каждой
ee точке. Области среды, в которых звуковое давление в данный момент времени максимально,
называются сгущениями, а области, в которых оно минимально, - разряжениями звуковой
волны. Расстояние между двумя соседними сгущениями (или разряжениями) равно длине  звуковой волны. Сгущения и разряжения распространяются относительно среды с фазовой скоростью
u волны. За один период колебаний T0  1/ 0 неподвижный источник излучает волну с длиной
0  uT0 . Если источник звука приближается к приемнику со скоростью v , то за время T0 источник приблизится к приемнику на расстояние vT0 , поэтому между двумя соседними сгущениями
расстояние, т.е. длина принимаемой звуковой волны, станет равной
1  uT0  vT0   u  v  / 0 ,
а частота –
1 
u
1
 0
u
.
uv
Если приемник также движется относительно среды со скоростью
то число

v2
навстречу источника звука,
сгущений звуковой волны, регистрируемых приемником, за 1 сек будет равным
   1     1 
v2
1
  1 (1 
v2
),
u
где  – дополнительное число принимаемых сгущений из-за движения приемника.
Таким образом, частота принимаемого звука будет:
  0
u  v2
.
uv
Это есть формула, выражающая эффект Доплера в акустике. Здесь скорости
v
и
v2
считают-
ся положительными, если источник и приемник звука приближаются друг к другу. Очевидно, при
этом принимаемая частота больше частоты излучаемого звука. Если источник и приемник удаляются друг от друга, то регистрируется обратный эффект.
Поглощение и отражение звука, реверберация.
Поглощение звука – это необратимый переход энергии звуковой волны в другие виды энергии, в частности, в теплоту. Поглощение звука характеризуется коэффициентом поглощения
 , которая определяется как обратная величина расстояния, на котором амплитуда волны
уменьшается в e  2, 72 раз. Другой характеристикой поглощения звука является коэффициент
   /  , ( 
потерь
- длина волны звука) или добротность
Q  1/  .
Величина

– есть
логарифмический декремент затухания.
Отражение звука. При падении на границу раздела двух однородных сред (воздух – стена,
воздух – водная поверхность и т.д.) плоская звуковая волна может частично отражаться и частично преломляться (проходить во вторую среду). Интенсивность отраженной волны характеризуется
R  I отр / I п , где I отр
коэффициентом отражения:
- интенсивность отраженной волны,
Iп
- интен-
сивность падающей волны. При вычислении коэффициента отражения следует учесть следующие
граничные условия: на границе двух сред должны быть равны давления и нормальные составляющие скорости частиц среды. При этом получается:
R
в
1
атм и
1
атм и
Медь
Сталь
падения
если
– отношение плотно-
– отношение скоростей распро-
u1  u 2 и углах падения, больших критического
   arcsin  u1 / u2  , имеет место полное внутреннее
отражение волн.
При отражении от границы двух сред фаза звуковой
воны  может меняться на величину  , или не меняться. Это зависит от отношения волновых сопротивлений этих сред. При нормальном падении волны (угол
  0 ) имеем:
 ,
 2 / 1
При
14  105
15  105
33  105
46  106
Стекло
u1 / u2
,
странения волн (относительный показатель преломления сред).
450
0 C)
0
Вода (при 20 C )
– угол падения,
стей масс сред,
429
0

где
кг / м2  с
00 C )
Кислород (при
( 2 / 1 )cos  (u1 / u2 ) 2  sin 2 
Волновое
сопротивление
Среда
Воздух (при
( 2 / 1 )cos  (u1 / u2 ) 2  sin 2 
   2 u 2 / 1u1  1 ;
  0,
если
   2 u 2 / 1u1  1 .
В первом случае говорят, что волна отражается от «более плотной» среды, а во втором – от
«менее плотной» среды.
Связь между амплитудами падающей (
A ),
отраженной (
Aотр )
и проходящей (
Aпр )
во вторую
среду волн, в случае нормального падения имеет вид
Aотр 
При
 1
1 
A,
1 
отраженная волна отсутствует, а при
Aпр 
 
2
A.
1 
- отсутствует проходящая волна. По-
следнее условие соблюдается при отражении звука, распространяющегося в воздухе, от поверхностей жидкостей и твердых тел.
Отраженная от какого-либо препятствия и принятая наблюдателем звуковая волна называется
эхо. Эхо различимо на слух, если принятый и посланный звуковые импульсы разделены интерва-
лом времени
  50  60 мс . Эхо становится многократным, если имеется несколько отражающих
поверхностей. В замкнутых объемах отдельные многократные эхо сливаются в сплошной отзвук,
вызывающий реверберацию.
Реверберация – это процесс постепенного затухания звука в закрытых помещениях после выключения его источника. Воздушный объем помещения представляет собой колебательную систему с большим числом собственных частот. Каждый из них характеризуется своим коэффициентом
затухания. Поэтому, возбужденные источником звуковые колебания разных частот затухают не
одновременно.
Длительность реверберации характеризуется временем реверберации – это время, за которое
интенсивность звука, после выключения его источника, уменьшается в миллион раз. Время реверберации – важнейший фактор, определяющий акустическое качество помещения. Существует
отдельная отрасль – архитектурная акустика, которая занимается именно этими вопросами.
Физиологическая акустика.
Здесь для характеристики звуковых ощущений применяются понятия высоты, тембра и громкости звука.
Высота – это качество звука, зависящее от ее частоты и оцениваемое на слух. С уменьшением
частоты высота звука понижается.
В отличие от интенсивности звука и среднеквадратичного давления, которые являются объективными характеристиками звуковой волны, громкость звука является субъективной оценкой
слухового ощущения. Громкость звука зависит не только от его среднеквадратичного давления
p3 ,
но и от чувствительности уха, которая неодинакова для звуков разной интенсивности и ча-
стоты. Так, например, если звуковое давление меньше некоторой величины, называемой порогом
слышимости, то такой звук ухом не воспринимается. Порог слышимости зависит от частоты звука, достигая минимума (порядка
p3  2  105 Н / м2 ) при частотах 1,5 – 3 кГц. С другой стороны,
достаточно интенсивные звуки не воспринимаются ухом как звуки и вызывают болевые ощущения
(рис.18.7). Минимальное значение
p3 , при
котором появляется это ощущение, называется поро-
гом болевого ощущения. Он максимален при частотах 0,5 – 1 кГц и составляет примерно
200 Н / м2 .
В плоскости
 v, p 
область слышимых звуков ограничена двумя пороговыми кривыми, пред-
ставленными на рис. 18.7.
Рис. 18.7
В акустике звуки, соответствующие синусоидальным волнам называются простыми, или чистыми тонами. Однако упругие волны, возбуждаемые реальными источниками звука, представляют собой совокупность синусоидальных волн с различными амплитудами и частотами. В зависимости от вида спектра частот и соответствующих им интенсивностей все звуки можно разбить на
две группы:
а) тональные, или музыкальные звуки, обладающие линейчатым спектром; таковы, например, звуки различных музыкальных инструментов;
б) шумы – звуки, обладающие сплошным спектром; например, шелест листьев, уличный шум,
шум морского прибоя и т.д.
При слуховом восприятии звука с линейчатым спектром возникает ощущение звука более или
менее определенного тона, называемого основным тоном. Частота основного тона
0
совпадает
с наименьшей частотой линейчатого спектра тонального звука. Тоны, соответствующие остальным
частотам спектра, называются обертонами. В случае периодического звука частоты обертонов
кратны νо, а сами обертоны называются гармониками.
Ультразвук.
Ультразвук - высокочастотные колебания в диапазоне
1013 Гц
2  104 - 109 Гц .
Область частот
109
-
называется гиперзвуком.
Для генерации, регистрации и анализа ультразвуковых волн используются главным образом
пьезоэлектрические и магнитострикционные излучатели и датчики (преобразователи).
Действие пьезоэлектрических излучателей основано на явлении обратного пьезоэлектрического эффекта. Пьезоэлектрические излучатели применяются для генерирования ультразвуков с частотами до 50  10 Гц.
Магнитострикционные излучатели применяются для получения низкочастотных ультразву6
ков (до 2  10 Гц). Их действие основано на явлении магнитострикции - изменении размеров
ферромагнитных тел в магнитном поле.
Ультразвуковые волны обладают рядом специфических свойств. Важнейшая их особенность
состоит в том, что, подобно свету, они могут излучаться в виде узких направленных пучков, называемых ультразвуковыми лучами. Это свойство является результатом малости длины
ультразвуковой волны. Отражение и преломление ультразвуковых лучей на границе раздела
двух сред происходит по законам геометрической оптики, установленным для световых лучей.
Поэтому для изменения направления распространения и фокусирования ультразвуковых лучей применяются зеркала различной формы, звуковые линзы, призмы и другие устройства,
действие которых на ультразвуковые лучи подобно действию на световые лучи одноименных
с ними оптических устройств.
На законе прямолинейного распространения ультразвуков основаны такие технически
важные применения этих волн, как ультразвуковая локация и дефектоскопия. Принцип
ультразвуковой локации состоит в следующем. Источник ультразвука излучает короткий сигнал, распространяющийся в определенном направлении до тех пор, пока на его пути не
встретится какое-либо препятствие, при отражении от которого образуется эхо-сигнал, распространяющийся в обратном направлении. Измеряя промежуток времени t между моментом посылки сигнала источником и моментом возвращения эхо-сигнала, можно определить
 ut / 2 , где u - скорость ультразвурасстояние
от источника сигнала до препятствия:
ка в среде. По изменению частоты эхо-сигнала, обусловленному эффектом Доплера, можно
определить величину и направление так называемой л у ч е в о й с к о р о с т и движущегося
препятствия - составляющей его скорости вдоль направления распространения сигнала. Ультразвуковые гидролокаторы широко применяются для измерения глубин моря, обнаружения подводных лодок, обнаружения крупных косяков рыб и т.д
Ультразвуковая локация в воздухе практически невозможна из-за чрезвычайно
5
сильного затухания ультразвуковых волн. Так, например, для волн с частотой 10 Гц амплитуда звукового давления в воздухе убывает в 100 раз на каждые 10 м расстояния от источника волн.
Ультразвук применяется для обнаружения внутренних дефектов (раковин, трещин, неоднородности структуры) в твердых телах. Это осуществляется с применением различных типов
ультразвуковых дефектоскопов. В теневом дефектоскопе источник и приемник ультразвукового луча располагаются напротив друг друга с противоположных сторон исследуемого тела.
Внутренние дефекты в теле вызывают рассеяние ультразвука и образуют «звуковую тень».
Поэтому интенсивность луча, прошедшего через такое тело, меньше, чем интенсивность луча,
прошедшего через аналогичное тело, не содержащее внутренних дефектов. «Просвечивая»
тело ультразвуком в различных местах и направлениях, можно определить форму, размеры и
5
расположение этих дефектов. Однако мелкие раковины и трещины не дают резкой «тени», и
их обнаружение таким способом затруднительно.
Более совершенен импульсный дефектоскоп, который по принципу действия подобен ультразвуковому локатору: обнаружение внутренних дефектов в теле производится по поступающим
от них эхо-сигналам. Расстояние от поверхности тела, на которой установлен источник коротких ультразвуковых сигналов, до внутренней раковины, трещины и т. д. определяется по
продолжительности промежутка времени между отправкой сигнала и приходом эхо-сигнала.
Благодаря большой амплитуде звукового давления, создаваемого мощными ультразвуками,
в жидкости возникает кавитация - непрерывно образуются и исчезают внутренние разрывы.
Исчезновение разрывов сплошности жидкости сопровождается кратковременным возрастанием
давления до многих сотен атмосфер. В связи с этим ультразвук обладает дробящим действием. Он разрушает находящиеся в жидкости твердые тела, микроорганизмы, сложные молекулы и т.д. Разрушающее действие ультразвука в жидкости на поверхность твердых тел заметно увеличивается при введении в нее мелких абразивных частиц. Это явление используется
для ультразвукового «сверления» отверстий различной формы в стекле, керамике, сверхтвердых сплавах. Для этой цели применяются источники ультразвука (ультразвуковые вибраторы),
наконечники которых имеют ту же форму, какую нужно придать отверстию в обрабатываемом
изделии…
Контрольные вопросы:
● Как образуются волны в упругой среде?
● Какими параметрами характеризуется волна?
● Чем отличаются продольные волны от поперечных волн?
● Что такое фазовая скорость волны?
● Как зависит от времени объемная плотность энергии упругой волны?
● Что характеризует вектор Пойтинга?
● Какие волны при наложении дают интерференцию?
● Чем отличается стоячая волна от бегущей?
● В чем заключается эффект Доплера?
● Чем характеризуется звук в физической акустике?
● Каковы характеристики звука в физиологической акустике?
● Каковы применения ультразвука?