061_neunet

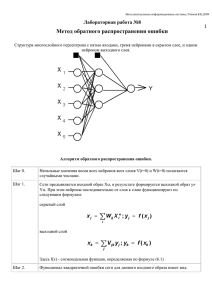
Интеллектуальные
Интеллектуальные информационные
информационные системы
системы
Д.А.
Д.А. Назаров
Назаров
(ред.
Декабрь
(ред. Декабрь 2012)
2012)
ОдноОдно- ии многослойные
многослойные нейронные
нейронные сети,
сети,
Обучение
Обучение методом
методом обратного
обратного распространения
распространения ошибки
ошибки
Осовский С. Нейронные сети для обработки информации / Пер. с польского
И.Д. Рудинского - М.: Финансы и статистика, 2002
Однослойная сеть
Однослойную сеть образуют нейроны, расположенные в одной плоскости. Каждый i-й
нейрон имеет поляризацию (сязь с весом w i0 , по которой поступает единичный сигнал),
а также множество связей с весами w ij , по которым поступают входные сигналы x j
.
Значения весов подбираются в процессе обучения сети, заключающемся в приближении
выходных сигналов y i к ожидаемым значениям d i . Мерой близости считается значение
целевой функции E (w ij ) . При использовании p обучающих векторов
⟨ ⃗x , d⃗ ⟩
для
обучения сети, включающей M выходных нейронов, целевая функция определяется
евклидовой метрикой в виде:
p
p
M
1
1
)
(k ) 2
E= ∑ ∥ y⃗( k )− d⃗( k )∥2= ∑ ∑ ( y (k
i −d i )
2 k =1
2 k =1 i=1
2
y2
y1
yM
…
1
wi j
…
x1
x2
x3
Рис. 1. Схема однослойной ИНС
3
xN
Расположенные на одном уровне нейроны функционируют независимо друг от друга,
поэтому возможности такой сети ограничиваются свойствами отдельных нейронов.
Несмотря на то, что однослойная сеть имеет небольшое практическое применение,
её продолжают использовать там, где для решения поставленной задачи задачи
достаточно и одного слоя нейронов.
Выбор архитектуры такой сети весьма прост. Количество входных нейронов
⃗x
(сенсоров) определяется размерностью входного вектора
d
выходных нейронов определяется размерностью вектора ⃗
, а количество
.
Обучение сети производится, как правило, с учителем и является точной копией
обучения одиночного нейрона.
4
Многослойный перцептрон (многослойная ИНС)
Многослойная сеть состоит из нейронов, расположенных на разных уровнях, причём,
помимо входного и выходного слоёв, имеется ещё, как минимум, один внутренний,
т. е. скрытый, слой.
Такая нейронная сеть также называется многослойным перцептроном.
1
w
1
(1)
10
v1
x1
...
w(2)
20
w(2)
1K
...
...
y1
v2
x2
xN
w(2)
10
w(1)
2N
vK
yM
w(2)
MK
w(1)
KN
Рис. 2. Двухслойная полносязная ИНС с одним скрытым слоем
5
Выходные сигналы нейронов скрытого слоя обозначаются
выходного слоя -
v j , j=1, 2,… , K
, а
y j , j=1, 2,… , M.
Пусть функция активации задана в сигмоидальной форме. С целью упрощения записи
будет использоваться расширенное обозначение входного вектора сети в виде
T
⃗x =( x 0, x 1, … , x N ) , где x 0=1 соответствует единичному сигналу поляризации. С
x сязаны два выходных вектора сети:
вектором ⃗
●
Вектор фактических выходных сигналов:
T
⃗y=( y 1, y 2, … , y M )
●
Вектор ожидаемых выходных сигналов:
d⃗ =(d 1, d 2, … , d M )T
(2)
и
для всех слоёв сети,
w(1)
w
ij
ij
чтобы при заданном векторе ⃗
x получить на выходе значения сигналов y i , которые
с требуемой точностью будут совпадать с ожидаемыми значениями d i ∀i=1,2 ,… , M
Цель обучения состоит в подборе таких значений весов
6
С учётом включения веса сигнала поляризации, выходной сигнал i -го нейрона
скрытого слоя описывается функцией:
vi = f
(
N
∑ w(1)ij x j
j =0
)
При этом для входа на следующем слое принимается
v 0 =1 . В выходном слое k -й
нейрон вырабатывает выходной сигнал, вычисляемый по формуле:
yk= f
(
K
∑ w(ki2) vi
i=0
) ( (
K
=f
N
∑ w (2)ki ∑ w(1)
ij x j
i=0
j=0
))
Из этой формулы видно, что на значение выходного слоя влияют веса обоих
слоёв.
Необходим способ обучения многослойных сетей с учётом влияния всех слоёв на
выход сети.
7
Алгоритм обратного распространения ошибки
Алгоритм обратного распространения ошибки (error back propagation) определяет
стратегию подбора весов многослойной сети с применением градиентных методов
оптимизации. Его основу составляет целевая функция, формулируемая, как
правило,в виде квадратичной суммы разностей между фактическими и ожидаемыми
⃗⟩
значениями выходных сигналов. В случае единичной обуающей выборки ⟨ ⃗x , d
целевая функция определяется в виде:
M
1
E (w)= ∑ ( y k −d k )2
2 k =1
При большем количестве обучающих выборок
j=1, 2, … , p
целевая функция
превращается в сумму по всем выборкам:
p
M
1
E (w)= ∑ ∑ ( y(k j )−d (k j) )2
2 j=1 k =1
Уточнение весов может проводиться после предъявления каждой обучающей выборки
(режим «онлайн») либо однократно после предъявления всех выборок, составляющих
цикл обучения (режим «оффлайн»)
8
Обучение производится в несколько этапов:
1.
⃗x
Предъявляется обучающая выборка
и рассчитываются значения сигналов
⃗x определяются значения выходных
сигналов v i скрытого слоя, а затем – значения y i нейронов выходного слоя (в случае
соответствующих нейронов сети. Для заданного
двухслойной сети) по формулам:
vi = f
2.
(
N
∑ w ij x j
(1)
j =0
)
,
yk= f
(
K
) ( (
K
∑ w vi = f
i=0
( 2)
ki
∑w
i=0
(2)
ki
N
∑ wij x j
(1)
j=0
))
Минимизируется значение целевой функции.
Если целевая функция непрерывна, то наиболее эффективным способом обучения
оказывается применение градиентных методов оптимизации, согласно которым
уточнение вектора весов производится по формуле:
w
⃗ ( k+1)= w
⃗ (k )+Δ w
⃗
Δw
⃗ =η p( w
⃗ ) , η - скорость обучения, p( w
где
⃗ ) - направление в многомерном
пространстве значений весовых коэффициентов w
⃗.
9
Обучение
многослойной
сети
с
применением
градиентных
методов
требует
определения вектора градиента для каждого слоя сети, что необходимо для
правильного выбора направления
p( w
⃗ ). Эта задача имеет очевидное решение только
для весов нейронов выходного слоя.
Для обучения внутренних слоёв необходимо учитывать влияние этих слоёв на
итоговый выход сети и ту погрешность, которая создаётся под их влиянием.
Для обучения внутренних слоёв с учетом влияния их погрешности была создана
специальная стратегия, называемая алгоритмом обратного распространения ошибки.
10
Как уже говорилось при рассмотрении алгоритма обучения нейрона с помощью
градиентного метода, веса нейронов корректируются в сторону убывания целевой
функции, т. е. в сторону, противоположную градиенту с координатами:
T
 ∇ 0 E , ∇ 1 E , ∇ 2 E ,... , ∇ N E 
∇ j E=
, где
∂E
∂ wij
Компонент градиента, как приводилось ранее, расписывается следующим образом:
dyi
∂ ui
∂E
∂E
=
⋅
⋅
=( y i −d i )⋅f ' (u i )⋅x j
∂ w ij
∂ yi
dui
∂ w ij
x1
Однако применить её можно только к
обучению нейронов выходного слоя.
.
.
.
xj
.
.
.
Для обучения внутренних слоёв
необходимо учитывать их влияние на
xN
целевую функцию.
11
w i1
w ij
w i0
++
wi N
ui
f (u i )
yi
Рассмотрим зависимость целевой функции от выхода j-го нейрона предпоследнего
n+1
∑
k =1
∂ E dy k ∂ u k
⋅ ⋅
=
∂ y k du k ∂ y j
K
n+1
∑ ∂∂ yE ⋅ f ' (u k )⋅w (n+1)
jk
k=1
k
...
∂E
=
∂ yj
K
yj
w jk
...
...
слоя (n < N):
yk
где суммирование производится по всем K нейронам
следующего слоя (n+1), сязанным с рассматриваемым j-м нейроном текущего слоя n.
Обозначим:
(n)
δj =
∂E
⋅f ' (u j ) , тогда получим рекуррентное соотношение:
∂ yj
[
∂E
⋅f ' (u j )=
(n)
∂ yj
При этом для выходного слоя N :
K n+1
( n+1)
∑ δk
k =1
(n+1)
⋅w jk
]
δ Nj =( y Nj −d j )⋅f ' (u j )
12
(n)
⋅ f ' (u j )=δ j
Таким образом, для произвольного слоя n компоненты градиента вычисляются:
(n) (n−1)
Δ w(n)
=−ηδ
ij
j yi
очевидно, что для первого слоя (n=1):
y(1)
i =x i
Иногда для устранения эффекта осцилляции вводят коэффициенты инерционности
обучения:
(n) (n−1)
(n)
Δ w(n)
(t+1)=−ηδ
y
+α
w
ij
j
i
ij (t) ,
∣α∣<1
или
(n)
( n) (n−1)
Δ w(n)
(t+1)=−η
μ
Δ
w
(t)+(1−μ)δ
[
],
ij
ij
j yi
13
∣μ∣<1
Алгоритм обратного распространения ошибок можно описать в следующем виде:
1.
1. Подать
Подать на
на вход
вход сигналы
сигналы
2.
2. Рассчитать
Рассчитать выход
выход внешнего
внешнего слоя
слоя
Если
Если ошибка
ошибка сети
сети существенна
существенна
E >ϵ
3.
3. Рассчитать
Рассчитать изменения
изменения весов
весов внешнего
внешнего слоя
слоя
δ(jN ) → Δ w(ijN )
4.
4. Рекуррентный
Рекуррентный рассчёт
рассчёт весов
весов нейронов
нейронов внутренних
внутренних слоёв
слоёв
(n)
δ(n)
→
Δ
w
j
ij , n<N
14
Останов
Останов