Отчет по дисциплине: Телекоммуникации
реклама

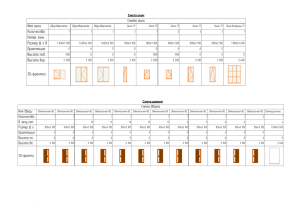
ÑÀÍÊÒ-ÏÅÒÅÐÁÓÐÃÑÊÈÉ ÃÎÑÓÄÀÐÑÂÅÍÍÛÉ ÏÎËÈÒÅÕÍÈ×ÅÑÊÈÉ ÓÍÈÂÅÐÑÈÒÅÒ Êàôåäðà êîìïüþòåðíûõ ñèñòåì è ïðîãðàìíûõ òåõíîëîãèé Îò÷åò ïî äèñöèïëèíå: Òåëåêîììóíèêàöèè Ëàáîðàòîðíàÿ ðàáîòà 2 Ñïåêòðû ïðîñòûõ ñèãíàëîâ Ïðåïîäàâàòåëü Áîãà÷ Í. Â. Âûïîëíèëà ñòóäåíòêà ãðóïïû 33501/4-2 Ïåðåòÿòüêî Å. Â. ÑÏá 2015 1 Öåëü Ïîëó÷èòü ïðåäñòàâëåíèå î ñâîéñòâàõ ñïåêòðîâ. 2 Ïîñòàíîâêà çàäà÷è  êîìàíäíîì îêíå MATLAB è â ñðåäå Simulink ïðîìîäåëèðóéòå ñëåäóþùèå òåñòîâûå ñèãíàëû: NP −1 ïîëèãàðìîíè÷åñêèé ñèãíàë y(t) = cos(nt) n=0 ïðÿìîóãîëüíûé èìïóëüñíûé ñèãíàë y(t) = Ï(t,Ti) òðåóãîëüíûé èìïóëüñíûé ñèãíàë y(t) = ∆(t,Ti) Ïîëó÷èòå èõ ñïåêòðû. 1 3 Õîä ðàáîòû Íèæå ïðåäñòàâëåí êîä â Matlab 2 1. Ïîëèãàðìîíè÷åñêèé ñèãíàë y(t) = NP −1 cos(nt). ×òîáû ïîëó÷èòü ïîëèãàðìîíè÷åñêèé n=0 ñèãíàë íóæíî ïðîñóììèðîâàòü íåñêîëüêî ãàðìîíè÷åñêèõ ñèãíàëîâ(cos èëè sin). Íà ðèñóíêå 1 ïðåäñòàâëåíííî èçîáðàæåíèå ïîëèãðàìíè÷åñêîãî ñèãíàëà ïîëó÷åííîãî â ðåçóëüòàòå ìîäåëèðîâàíèÿ ñèãíàëà. Ðèñ.1 Íà ðèñóíêå 2 ïðåäñòàâëåí ñïåêòð ïîëèãàðìîíè÷åñêîãî ñèãíàëà. Ðèñ.2 3 Èñïîëüçóÿ ñðåäñòâà Simulink áûëî ïðîâåäåíî ìîäåëèðîâàíèå. Ðåçóëüòàòû ìîäåëèðîâàíèÿ è ñàìè ìîäåëè ïðåäñòàâëåíû íèæå. Èñïîëüçóÿ ñðåäñòâà Simulink ñëîæèëè íåñêîëüêî ãàðìîíè÷åñêèõ ñèãíàëîâ. Ðèc.3 Ðèñ.4 Ïîëèãàðìîíè÷åñêèé ñèãíàë ñ ïîìîùüþ ñðåäñòâà Simulink 4 Ðèñ.5 Ñïåêòð ïîëèãàðìîíè÷åñêîãî ñèãíàëà 5 2. Ïðÿìîóãîëüíûé èìïóëüñíûé ñèãíàë y(t) = Ï(t,Ti) Ïðÿìîóãîëüíûé èìïóëüñ ñ åäåíè÷íîé àìïëèòóäîé îáîçíà÷àåòñÿ Ï(t,Ti). Ïåðâûé àðãóìåíò îáîçíà÷àåò ïîëîæåíèå èìïóëüñà íà ãîðèçîíòàëüíîé îñè. Âòîðîé àðãóìåíò îçíà÷àåò øèðèíó èìïóëüñà. Âåëè÷èíà ðàâíàÿ T/t íàçûâàåòñÿ ñêâàæíîñòüþ èìïóëüñíîé ïîñëåäîâàòåëüíîñòè. Ñïåêòð ïðÿìîóãîëüíîãî èìïóëüñà îïðåäåëÿåòñÿ âûðàæåíèåì: R∞ R (T n/2) Ô(f) = −∞ (t, T n)e−j2πf t dt = −(T n/2) e−j2πf t dt = sin(πf T n)/πf Ðèñ.6 Ïðÿìîóãîëüíûé ñèãíàë ïîëó÷åííûé â ðåçóëüòàòå ìîäåëèðîâàíèÿ Ðèñ.7 Ñïåêòð ïðÿìîóãîëüíîãî ñèãíàëà 6 Èñïîëüçóÿ ñðåäñòâà Simulink ïîëó÷èëè ïðÿìîóãîëüíûé ñèãíàë(Ðèñ. 9) Ðèc.8 Ðèñ.9 Ïðÿìîóãîëüíûé èìïóëüñ ñ ïîìîùüþ ñðåäñòâà Simulink 7 Ðèñ.10 Ñïåêòð ïðÿìîóãîëüíîãî èìïóëüñà 8 3. Òðåóãîëüíûé èìïóëüñíûé ñèãíàë y(t) = δ (t,Ti) Òðåóãîëüíûé ñèììåòðè÷íûé èìïóëüñ, ñåðåäèíà êîòîðîãî ñîîòâåòñâóåò t = 0, äëèòåëüíîñòü ðàâíà Ti, à àìïëèòóäà åäèíèöå. Òàêîé èìïóëüñ ìîæíî ïðåäñòàâèòü â â èäå ñâåðòêè äâóõ îäèíàêîâûõ ïðÿìîóãîëüíûõ èìïóëüñîâ äëèòåëüíîñòüþ Ti/2. ∆(t,Tn) = (2/Tn)Ï(t,(Tn/2))*Ï(t,(Tn/2)) Ðèñ.11 Òðåóãîëüíûé ñèãíàë ïîëó÷åííûé â ðåçóëüòàòå ìîäåëèðîâàíèÿ Ðèñ.12 Ñïåêòð òðåóãîëüíîãî ñèãíàëà 9 Èñïîëüçóÿ ñðåäñòâà Simulink ïîëó÷èëè òðåóãîëüíûé ñèãíàë. Ðèc.13 Ðèñ.14 Òðåóãîëüíûé ñèãíàë ñ ïîìîùüþ ñðåäñòâà Simulink 10 Ðèñ.15 Ñïåêòð òðåóãîëüíîãî ñèãíàëà 11 4 Âûâîä  äàííîé ðàáîòå áûëè ïîëó÷åíû ñèãíàëû ðàçëè÷íûõ âèäîâ: ïîëèãàðìîíè÷åñêèé, òðåóãîëüíûé è ïðÿìîóãîëüíûé. Ïîëèãàðìîíè÷åñêèé ñèãíàë áûë ïîëó÷åí ñóììèðîâàíèåì êîñèíóñîâ. Ïðÿìîóãîëüíûé ñèãíàë áûë ïîëó÷åí ñ ïîìîùüþ ñïåöèàëüíîé ôóíêöèè, ãåíåðèðóþùåé ïðÿìîóãîëüíûå èìïóëüñû. Ïðèìåíÿÿ îïåðàöèþ ñâåðòêè ê äâóì ïðÿìîóãîëüíûì èìïóëüñàì ïîëó÷àåì ñèãíàë òðåóãîëüíîãî âèäà.  ðåçóëüòàòå òàêîãî ïðåîáðàçîâàíèÿ áóäóò ïîëó÷åíû 2 ëèíåéíûå ôóíêöèè: ñ ïîëîæèòåëüíûì è îòðèöàòåëüíûì êîýôôèöèåíòîì íàêëîíà. Âñå âûøå ïåðå÷èñëåííûå ñèãíàëû áûëè òàê æå ïîëó÷åíû â ñðåäå Simulink. Äëÿ ïîëó÷åíèÿ òðåóãîëüíîãî èìïóëüñà â ýòîé ñðåäå áûëè ñîåäèíåíû ãåíåðàòîð ïðÿìîóãîëüíûõ èìïóëüñîâ è ôèëüòð ñ ïðÿìîóãîëüíûì îêíîì. Áûë èñïîëüçîâàí ÊÈÕ ôèëüòð, êîòîðûé ïîçâîëèë ñãåíåðèðîâàòü íåîáõîäèìûé ñèãíàë, ïîòîìó ÷òî îí âûïîëíèë ñâåðòêó ñèãíàëà ñ ìàññèâîì èç 1. 12