Для реактивного двухполюсника построить схему - RGR

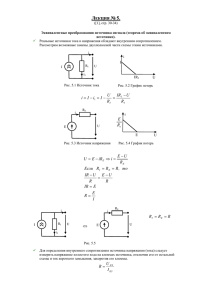
Контрольная работа №1
Задача 1
( 5 4)
Для реактивного двухполюсника построить схему обратного двухполюсника и
рассчитать его элементы.
Схема реактивного двухполюсника приведена на рис. 1.
C1
L2
а)
L1
Рис. 1. Исходный реактивный двухполюсник.
Значения элементов двухполюсников:
L1 = 10 мГн; C1 = 0.3 мкФ;
L2 = 18 мГн.
Коэффициент перехода R2 = k = 0.7 Ом2.
Для решения задачи нужно выполнить следующее:
используя правила, построить схему обратного двухполюсника относительно
заданного;
рассчитать значения элементов обратного двухполюсника по данным исходного
двухполюсника при указанном коэффициенте перехода (отношении между значениями
элементов двухполюсников);
определить все резонансные частоты и характеры резонансов исходного и обратного
двухполюсников;
построить частотные характеристики реактивных сопротивлений обоих
двухполюсников (Z = jx (ω)) и показать характеристические строки двухполюсников с
расположенными на них полюсами и нулями;
указать, к каким классам канонических схем двухполюсников относятся оба
двухполюсника и в чем особенность их свойств;
рассчитать реактивные сопротивления двухполюсников на одной частоте, лежащей в
каждой из частотных полос: 0 - ω1, ω1 - ω2, .... ωn - ∞, где ω1, ω2, ωn, - соответственно первая,
вторая и последняя резонансные частоты.
В заключение следует ответить на вопросы:
1. Какие схемы двухполюсников называются каноническими, в чем их особенности и
практическое значение?
2. В каких устройствах автоматики, телемеханики и связи используются обратные
двухполюсники?
Рассмотрим двухэлементные LC двухполюсники.
Последовательное соединение (рис. 2).
C
L
Рис. 2. Последовательное соединение LC.
Сопротивление двухполюсника:
Z (ω ) = jωL +
1
= jL
jωC
ω2 −
ω
1
2
2
LC = jL ω − ω р ,
ω
(1)
где
ωр2 =
1
LC
- резонансная частота (резонанс напряжений).
Проводимость двухполюсника:
Y (ω ) =
1
1
ω
=−j ⋅ 2
.
Z (ω )
L ω − ωр2
Параллельное соединение (рис. 3).
C
L
Рис. 3. Параллельное соединение LC.
Проводимость двухполюсника:
Y (ω ) =
1
jω L
+ jωC = jC
ω2 −
ω
1
2
2
LC = jC ω − ω р ,
ω
где
ωр2 =
1
LC
- резонансная частота (резонанс токов).
Сопротивление двухполюсника:
Z (ω ) =
1
1
ω
=−j ⋅ 2
.
Y (ω )
C ω − ωр2
(2)
Найдем сопротивление исходного двухполюсника (рис. 1).
⎛
⎞
1
ω
⎟=
Z (ω ) = Z 2 (ω ) + Z 1 (ω ) = jωL2 + ⎜⎜ − j ⋅ 2
2 ⎟
C
ω
−
ω
1
1 ⎠
⎝
⎛
= jL2 ⋅
1 ⎞⎞
⎛
⎟⎟
ω ⎜⎜ ω 2 − ⎜⎜ ω1 2 +
L2 C1 ⎟⎠ ⎟⎠
⎝
⎝
(ω 2 − ω1 )
2
ω (ω 2 − ω 2 2 )
= jL2 ⋅
,
2
(ω 2 − ω1 )
где
*
ω1 2 =
1
=
L1C1
ω 2 2 = ω1 2 +
1
=
L2 C1
1
8
−2
1 × 10
−7
= 3.333 × 10
2
1/с ;
⋅ 3 × 10
1
8
3.333 × 10 +
8
−2
1.8⋅ 10
−7
= 5.185 × 10
2
1/с ;
⋅ 3 × 10
Сопротивление исходного двухполюсника:
ω (ω 2 − ω 2 2 )
Z (ω ) = jL2 ⋅
,
2
(ω 2 − ω1 )
(3)
где
2
8
2
2
8
2
L2 = 0.018 Гн; ω 1 = 3.333 × 10 1/с ; ω 2 = 5.185 × 10 1/с .
Рассчитаем значения элементов обратного двухполюсника.
Для исходного двухполюсника с сопротивлением заданным формулой (3), сопротивление
обратного двухполюсника будет:
Z ′(ω ) = − j
k (ω 2 − ω12 )
,
L2 ω (ω 2 − ω2 2 )
(4)
где
Z·Z' = k = 0.7 Ом2 – постоянный множитель, зависящий от значений элементов схемы.
Существует четыре схемы реализации двухполюсника, заданного формулой (4), см. табл. 1.
Выберем схему реализации (рис. 4) разложением сопротивления Z'(ω) на простые дроби:
C'2
С'1
L'2
Рис. 4. Схема реализации обратного двухполюсника.
Найдем значения элементов обратного двухполюсника.
Z ′(ω ) = Z1 (ω ) + Z 2 (ω ) =
⎛
1
1
ω ⎞
+⎜− j ⋅ 2
⎟=
jωC1′ ⎝ C2′ ω − ω2 2 ⎠
⎛ 2
C2′ ⎞
2
⎜ ω − ω2 ′
⎟
C1 + C2′ ⎠
C ′ + C2′ ⎝
k (ω 2 − ω12 )
j
=−j 1
⋅
=
−
⋅
=.
C1′ ⋅ C2′
L2 ω (ω 2 − ω2 2 )
ω (ω 2 − ω2 2 )
Находим:
ω12 = ω2 2 ⋅
C2′
C ′ + C2′ ω2 2 ω2 2
C′
⇒ 1
= 2;
= 1+ 1 ;
2
ω1
ω1
C1′ + C2′
C2′
C2′
L2 ω2 2
k C1′ + C2′ 1 C1′ + C2′ 1 ω2 2
′
=
=
=
⇒
=
C
.
1
L2 C1′ ⋅ C2′ C1′ C2′
C1′ ω12
k ω12
ω2 2
C1′
ω12
L2 ω2 2
′
′
=
1
+
⇒
C
=
C
=
.
2
ω12
C2′
ω2 2 − ω12 1 k ω2 2 − ω12
Получим:
C1′ =
*
L2 ω2 2
k ω12
C2′ =
L2 ω2 2
.
k ω2 2 − ω12
По формуле для резонансной частоты находим:
L2′ =
1
;
ω2 ⋅ C2′
2
Вычисляем значения элементов обратного двухполюсника:
C1′ =
C2′ =
L2 ω2 2
=
k ω12
L2 ω2 2
=
k ω2 2 − ω12
L2′ =
1
=
ω2 ⋅ C2′
2
8
0.018 5.185 × 10
⋅
= 0.04 Ф;
0.7 3.333 × 108
8
0.018
5.185 × 10
⋅
= 0.072 Ф;
0.7 5.185 × 108 − 3.333 × 108
1
−8
8
= 2.679 × 10
Гн;
5.185 × 10 ⋅ 0.072
Сопротивление обратного двухполюсника:
Z ′(ω ) = − j
k (ω 2 − ω12 )
,
L2 ω (ω 2 − ω2 2 )
где
2
2
k
2
2
8
8
= 38.89 Ом/с; ω 1 = 3.333 × 10 1/с ; ω 2 = 5.185 × 10 1/с .
L2
Параметры схемы (рис. 4) обратного двухполюсника:
−8
C'1 = 0.04 Ф; C'2 = 0.072 Ф; L'2 = 2.679 × 10
Гн.
Характеры резонансов исходного и обратного реактивных двухполюсников.
Исходный двухполюсник (рис. 5).
ω2
0
∞
ω1
C1
Z (ω ) = jL2 ⋅
a)
ω (ω − ω 2 )
,
2
(ω 2 − ω1 )
2
2
L2
а)
L1
б)
в)
Рис. 5.
Частота резонанса ω2 образована последовательным включением катушки L2 и контура
L1C1 (резонанс напряжений). Такие колебания возможны при замкнутых внешних зажимах
двухполюсника.
Частота резонанса ω1 представляет собой частоту собственных колебаний
колебательного контура L1C1 (резонанс токов). Такие колебания возможны при разомкнутых
внешних зажимах двухполюсника.
Обратный двухполюсник (рис. 6).
ω1
∞
ω2
0
a)
C'2
k (ω 2 − ω12 )
Z ′(ω ) = − j
,
L2 ω (ω 2 − ω2 2 )
С'1
L'2
б)
в)
Рис. 6.
Частота резонанса ω2 образована параллельным включением L'2C'2 (резонанс токов).
Такие колебания возможны при разомкнутых внешних зажимах двухполюсника.
Частота резонанса ω1 представляет собой частоту собственных колебаний цепи,
образованной последовательным соединением C'1L'2C'2 (резонанс напряжений). Такие
колебания возможны при замкнутых внешних зажимах двухполюсника.
Характеристические строки двухполюсников изображены на рис. 5. а) и рис. 6. а).
Частотные характеристики реактивных двухполюсников изображены на рис.7, 8.
В табл.1 дана классификация реактивных двухполюсников по характеристическим
строкам. Исходный двухполюсник относится к первому типу, схема 1. Обратный
двухполюсник относится ко второму типу, схема 3.
Особенность свойств двухполюсников (рис. 5, 6):
- для всех реактивных двухполюсников в выражениии для сопротивления числитель
является четным, а знаменатель нечетным по частоте (либо наоборот);
- двухполюсник (рис. 6) не пропускает постоянный ток, обратный ему (рис. 5) - пропускает;
- процессы в цепях, составленных из катушек индуктивности и конденсаторов с высокой
добротностью не сопровождаются сколь-нибудь значительным выделением энергии.
x(ω), Ом
3000
ω1
2000
1000
0
5000
1 .10
4
1.5 .10
4
2 .10
4
2.5 .10
4
3 .10
4
ω, 1/c
1000
2000
Рис. 7. Частотная характеристика исходного двухполюсника.
x' (ω), Ом
ω2
0.01
0
5000
4
1 .10
4
1.5 .10
4
2 .10
4
2.5 .10
4
3 .10
0.01
0.02
Рис. 8. Частотная характеристика обратного двухполюсника.
ω, 1/c
Рассчитаем реактивные сопротивления двухполюсников на одной частоте, лежащей в
каждой из частотных полос: 0 – ω1, ω1 – ω2, .... ωn – ∞,
*
Выберем следующие часторы:
3
4
ω 01 = 9.13 × 10 1/c; ω 12 = 2.05 × 10 1/c;
4
ω 2∞ = 3.42 × 10 1/c.
Для исходного двухполюсника:
2
8
2
8
ω − 5.185⋅ 10
Z ( ω ) = j⋅ 1.8⋅ 10 ⋅ ω ⋅
-2
ω − 3.333⋅ 10
(
3
) = 286j
(
4
(
4
Z 9.13 × 10
Ом;
) = −417j
Z 2.05 × 10
) = 479j
Z 3.42 × 10
Ом;
Ом;
Для обратного двухполюсника:
Z' ( ω ) = −38.89 j⋅
2
8
ω − 3.333⋅ 10
(
2
(
3
(
4
(
4
)
8
ω ⋅ ω − 5.185⋅ 10
) = −2.45j × 10− 3
Z' 9.13 × 10
) = 1.68j × 10− 3
Z' 2.05 × 10
Z' 3.42 × 10
) = −1.46j × 10− 3
Ом;
Ом;
Ом;