АНАЛИЗ ЧУВСТВИТЕЛЬНОСТИ РЕЗУЛЬТАТОВ РАСЧЕТОВ

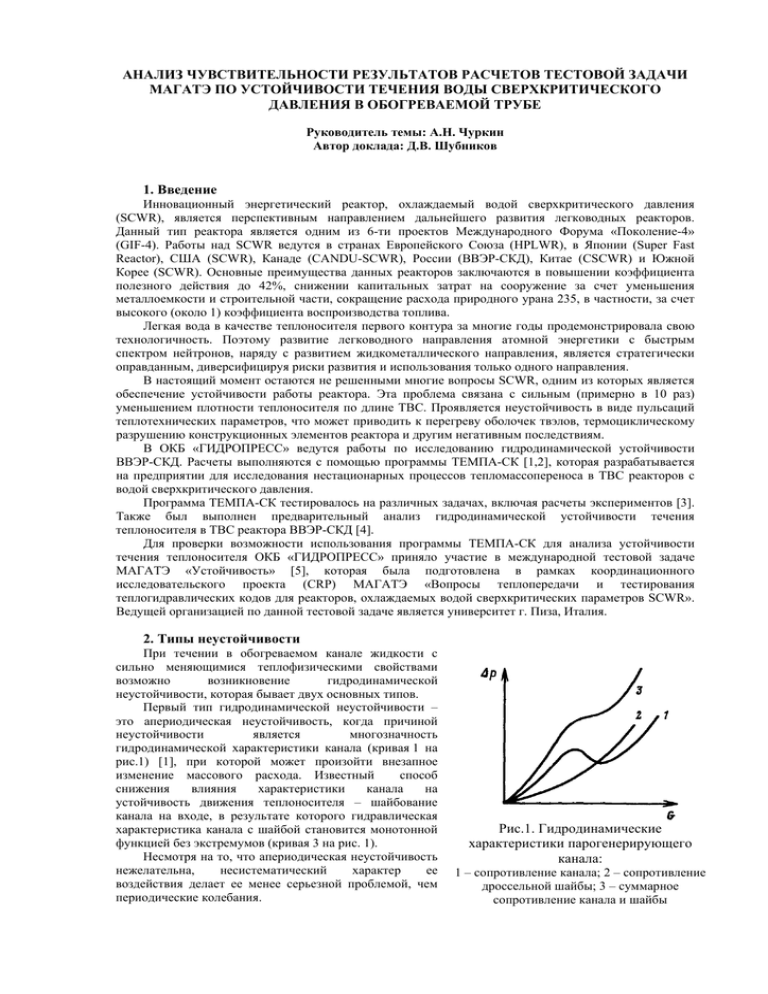
АНАЛИЗ ЧУВСТВИТЕЛЬНОСТИ РЕЗУЛЬТАТОВ РАСЧЕТОВ ТЕСТОВОЙ ЗАДАЧИ
МАГАТЭ ПО УСТОЙЧИВОСТИ ТЕЧЕНИЯ ВОДЫ СВЕРХКРИТИЧЕСКОГО
ДАВЛЕНИЯ В ОБОГРЕВАЕМОЙ ТРУБЕ
Руководитель темы: А.Н. Чуркин
Автор доклада: Д.В. Шубников
1. Введение
Инновационный энергетический реактор, охлаждаемый водой сверхкритического давления
(SCWR), является перспективным направлением дальнейшего развития легководных реакторов.
Данный тип реактора является одним из 6-ти проектов Международного Форума «Поколение-4»
(GIF-4). Работы над SCWR ведутся в странах Европейского Союза (HPLWR), в Японии (Super Fast
Reactor), США (SCWR), Канаде (CANDU-SCWR), России (ВВЭР-СКД), Китае (CSCWR) и Южной
Корее (SCWR). Основные преимущества данных реакторов заключаются в повышении коэффициента
полезного действия до 42%, снижении капитальных затрат на сооружение за счет уменьшения
металлоемкости и строительной части, сокращение расхода природного урана 235, в частности, за счет
высокого (около 1) коэффициента воспроизводства топлива.
Легкая вода в качестве теплоносителя первого контура за многие годы продемонстрировала свою
технологичность. Поэтому развитие легководного направления атомной энергетики с быстрым
спектром нейтронов, наряду с развитием жидкометаллического направления, является стратегически
оправданным, диверсифицируя риски развития и использования только одного направления.
В настоящий момент остаются не решенными многие вопросы SCWR, одним из которых является
обеспечение устойчивости работы реактора. Эта проблема связана с сильным (примерно в 10 раз)
уменьшением плотности теплоносителя по длине ТВС. Проявляется неустойчивость в виде пульсаций
теплотехнических параметров, что может приводить к перегреву оболочек твэлов, термоциклическому
разрушению конструкционных элементов реактора и другим негативным последствиям.
В ОКБ «ГИДРОПРЕСС» ведутся работы по исследованию гидродинамической устойчивости
ВВЭР-СКД. Расчеты выполняются с помощью программы ТЕМПА-СК [1,2], которая разрабатывается
на предприятии для исследования нестационарных процессов тепломассопереноса в ТВС реакторов с
водой сверхкритического давления.
Программа ТЕМПА-СК тестировалось на различных задачах, включая расчеты экспериментов [3].
Также был выполнен предварительный анализ гидродинамической устойчивости течения
теплоносителя в ТВС реактора ВВЭР-СКД [4].
Для проверки возможности использования программы ТЕМПА-СК для анализа устойчивости
течения теплоносителя ОКБ «ГИДРОПРЕСС» приняло участие в международной тестовой задаче
МАГАТЭ «Устойчивость» [5], которая была подготовлена в рамках координационного
исследовательского проекта (CRP) МАГАТЭ «Вопросы теплопередачи и тестирования
теплогидравлических кодов для реакторов, охлаждаемых водой сверхкритических параметров SCWR».
Ведущей организацией по данной тестовой задаче является университет г. Пиза, Италия.
2. Типы неустойчивости
При течении в обогреваемом канале жидкости с
сильно меняющимися теплофизическими свойствами
возможно
возникновение
гидродинамической
неустойчивости, которая бывает двух основных типов.
Первый тип гидродинамической неустойчивости –
это апериодическая неустойчивость, когда причиной
неустойчивости
является
многозначность
гидродинамической характеристики канала (кривая 1 на
рис.1) [1], при которой может произойти внезапное
изменение массового расхода. Известный
способ
снижения
влияния
характеристики
канала
на
устойчивость движения теплоносителя – шайбование
канала на входе, в результате которого гидравлическая
характеристика канала с шайбой становится монотонной
функцией без экстремумов (кривая 3 на рис. 1).
Несмотря на то, что апериодическая неустойчивость
нежелательна,
несистематический
характер
ее
воздействия делает ее менее серьезной проблемой, чем
периодические колебания.
Рис.1. Гидродинамические
характеристики парогенерирующего
канала:
1 – сопротивление канала; 2 – сопротивление
дроссельной шайбы; 3 – суммарное
сопротивление канала и шайбы
Второй тип гидродинамической неустойчивости – это периодическая неустойчивость. Она
подразделяется на три класса:
1) периодическая неустойчивость в одиночном канале;
2) периодическая неустойчивость в системе параллельных каналов (характерно для активной
зоны, состоящей из чехловых ТВС);
3) периодическая неустойчивость в контуре циркуляции теплоносителя (характерно для
двухконтурной РУ с естественной циркуляцией теплоносителя в первом контуре).
Данная статья направлена на исследование периодической неустойчивости в одиночном канале.
Этот тип неустойчивости называют также «канальная неустойчивость» или «колебания волн
плотности». Периодическая неустойчивость связана с наличием запаздывающих во времени обратных
связей между расходами на входе и выходе из канала и его гидравлическим сопротивлением.
3. Описание тестовой задачи МАГАТЭ «Устойчивость»
В данной задаче сверхкритическая жидкость движется в обогреваемой трубе длиной L=4,27 м и
внутренним диаметром D=8,36 мм. Тепловой поток с поверхности трубы равномерный по длине.
Перепад давления на входе и выходе зависит от постоянных коэффициентов местного сопротивления
(Кin=20, Кout варьируется от 2 до 20). Шероховатость принята равной ε=2,5·10-5 м. Рассматривается как
вертикальная ориентация трубы, так и горизонтальная.
Схематическое изображение рабочего участка задачи представлено на рис. 2.
Рис.2. Схема рабочего участка задачи.
В качестве граничных условий задается давление и температура во входной камере, а также
давление в выходной камере. Перепад давления на трубе выбирался из условия обеспечения расхода
жидкости в холодном состоянии в диапазоне 0,04 – 0,08 кг/с.
В тестовой задаче предлагалось сделать расчеты для различных типов жидкостей, а для воды – для
различных давлений. Это объясняется тем, что необходим более глубокий анализ влияния свойств
жидкости на механизм зарождения неустойчивости. Перечень рассматриваемых в задаче жидкостей и
соответствующие давления в выходной камере приведены в таблице 1. Поскольку в программе
ТЕМПА-СК в данный момент реализован расчет свойств только воды, и поскольку давление 30 и
40 МПа не являются характерными для ВВЭР-СКД, был выполнен поиск границ устойчивого течения
воды с давлением 25 МПа. В дальнейшем возможны расчеты и для остальных типов жидкости,
указанных в задаче.
Таблица 1
Рассматриваемые в задаче жидкости.
Жидкость
Давление, МПа
Вода
25, 30, 40
Углекислый газ (СО2)
8,0
Фреон (R23)
5,7
Аммиак
15,0
Целью расчета является определение параметров системы, при которых начинается периодическая
неустойчивость. Эти параметры было предложено объединить в безразмерные комплексы NSPC и NTPC
[6].
NSPC – безразмерный комплекс, определяющий недогрев жидкости до псевдокритической
температуры на входе в обогреваемый канал (sub-pseudocritical number):
N SPC =
β pc
C p pc
⋅ ( hpc − hin ) .
NTPC – безразмерный комплекс, определяющий подогрев жидкости в канале (trans-pseudocritical
number):
NTPC =
β pc Q
.
⋅
C p pc G
Так как температура и давление жидкости на входе не изменяются в ходе расчета, то NSPC также не
меняется. Для ряда предложенных значений NSPC производится отдельный расчет по определению
мощности, при которой возникают колебания параметров теплоносителя и течения. Алгоритм
определения границ неустойчивости следующий:
за несколько секунд производится быстрый рост мощности до значения, при котором
колебания еще не начались. Это необходимо для сокращения времени расчета, и никак не
влияет на последующее развитие событий (величина скачка уточняется предварительным
расчетом);
после скачка производится медленное увеличение мощности до того момента, когда
возникнут колебания;
данные о расходе через канал и мощности в момент начала колебаний фиксируются;
производится расчет NTPC гр;
значение NTPC гр заносится в сравнительную таблицу.
Момент начала колебаний фиксируется по формальному критерию: локальное повышение расхода
на фоне его медленного уменьшения в процессе разогрева.
Описанный выше алгоритм поиска границы неустойчивости работает в том случае, если скорость
увеличения мощности достаточно мала, чтобы имитировать квазистационарный режим.
По результатам расчетов заполнялась сравнительная таблица, единая для всех участников
(Таблица 2).
Таблица 2
Сравнительная таблица результатов
Имя участника
Вариант
Ориентация канала
Nspc
Kout=20
Kout=20
Ntpc,
Тип колебаний
граничное
Периодический
или
апериодический
Обозначение
D0.5V-K20 to K2
V
D1.0V-K20 to K2
V
1
D1.5V-K20 to K2
V
1,5
D2.0V-K20 to K2
V
2
D2.5V-K20 to K2
V
2,5
D3.0V-K20 to K2
V
3
Kout=10
Ntpc,
граничное
Kout=10
Тип колебаний
Kout=5
Kout=5
Kout=2
Ntpc,
Тип колебаний
Ntpc,
граничное
граничное
Kout=2
Тип колебаний
Периодический
или
апериодический
Периодический
или
апериодический
Периодический
или
апериодический
0,5
После того, как все участники передали в ведущую организацию (университет г. Пиза) результаты
своих расчетов, были открыты результаты расчетного линейного анализа устойчивости, выполненного
проф. Амбросини, которые показаны на рис. 3 линиями. Пунктирные и сплошные линии получены для
различной степени нодализации расчетной области при решении линеаризованной системы уравнений.
На этом же рисунке показанные значками результаты, полученные по коду RELAP.
Рис.3. Результаты, полученные методом линейного анализа.
С представленными на рис. 3 результатами линейного анализа сравнивались результаты расчетов
всех участников.
4. Результаты расчета
Расчет производился по указанному выше алгоритму для воды под давлением P=25МПа.
Сравнение результатов расчетов с результатами проф. Амбросини представлено в таблице 3 и на рис. 4.
Таблица 3
Полученные результаты расчета в ОКБ «ГИДРОПРЕСС» и сравнение их с результатами
линейного анализа устойчивости
Kout
NSPC
NTPC гр (Ambrosini)
NTPC гр (ГП)
20
0,5
3,02
3,21
1
2,61
2,8
1,5
2,80
2,93
2
3,15
3,35
2,5
3,59
3,73
10
1,5
3,24
3,53
5
1,5
3,75
4,28
Рис. 4 Результаты базового расчета ОКБ «ГИДРОПРЕСС» в сравнении с результатами
линейного анализа устойчивости
Как показывает сравнение, имеются отличия в расчетных значениях NTPC гр, особенно для значений
Kout равных 10 и 5. Для значений Kout = 2 результаты не были получены из-за превышения выходной
температуры воды значения 800 ºС, которая является предельным значение для программы ТЕМПА-СК.
Из рис. 4 видно, что по результатам расчетов ОКБ «ГИДРОПРЕСС» неустойчивость возникала при
больших значениях NTPC гр. , т.е. при большей мощности канала.
В связи с обнаруженными отличиями в результатах расчетов ОКБ «ГИДРОПРЕСС» и проф.
Амбросини возникла необходимость произвести анализ чувствительности результатов, для определения
влияния того или иного параметра на результаты расчета. Это и являлось целью данной работы.
5. Анализ чувствительности
Анализ чувствительности, приведенный в данном докладе, состоит из следующих этапов:
1) выполнение вариантных расчетов с измененными параметрами расчетной модели (поправки на
неизотермичность потока, количество слоев, время нагрева и т.д.) для Kout=20;
2) выбор параметров, которые в значительной мере влияют на результаты расчета;
3) совмещение параметров для получения наибольшего влияния на результат;
4) расчет по рекомендованным совмещенным параметрам для Kout=10 и Kout=5;
5) сравнение с результатами, полученными методом линейного анализа.
На первом этапе выполнена серия расчетов с изменением только одного параметра расчетной
модели по отношению к базовому варианту для Kout=20 и NSPC =1,5, результаты которого представлены
в разделе 4. Результаты расчетов приведены на рис. 5 – 9. Черным кружком выделены результаты и
значения параметров, которые были в базовом расчете.
3,05
3
NTPC гр
2,95
2,9
2,85
2,8
2,75
17
18
19
20
Местное сопротивление
ТЕМПА-СК
Ambrosini
Рис. 5. Влияние местного сопротивления на выходе на значение NTPC гр
21
3
2.9
2.85
2.8
2.75
0
50
100
150
200
250
300
350
400
Количество слоев
ТЕМПА-СК
Ambrosini
Рис. 6. Влияние количества слоев в расчетной модели на значение NTPC гр
3.05
3
2.95
NTPC гр
NTPC гр
2.95
2.9
2.85
2.8
2.75
0
5
10
15
20
25
30
35
40
Скорость повышения мощности (Вт/с)
ТЕМПА-СК
Ambrosini
Рис. 7. Влияние скорости повышения мощности на значение NTPC гр
45
2.98
2.96
2.94
NTPC гр
2.92
2.9
2.88
2.86
2.84
2.82
2.8
2.78
0
1
2
3
4
5
Поправка на трение
Без поправки
Кириллов
Попов
Попов (упрощ.)
Тарасова и Леонтьев
Михеев
Ambrosini
Рис. 8. Влияние поправки на неизотермичность потока для коэффициента трения
2.98
2.96
2.94
2.92
NTPC гр
2.9
2.88
2.86
2.84
2.82
2.8
2.78
0
1
2
3
4
Поправки на критерий Нуссельта
Не учит
Кириллов
Джексон и Фистер
Джексон
Краснощеков и Протопопов
Краснощеков
Ambrosini
Рис. 9. Влияние поправки на неизотермичность потока для коэффициента теплоотдачи
5
В таблице 4 приведены параметры, рекомендованные для выполнения расчетов.
Таблица 4
Рекомендованные параметры расчетной модели.
Название параметра
Значение
Поправка на критерий Нуссельта
Краснощеков-Протопопов
NTPC гр
2,93
Поправка на трение
Попов
2,92
Количество слоев
Скорость повышения мощности
91
2,5 Вт/с
2,91
2,84
Как видно из сравнения, наибольшее влияние на результаты расчетов оказывает уменьшение
скорости нагрева. Это объясняется тем, что с уменьшением скорости нагрева, режим приближается к
квазистационарному. Успевают развиться колебания, которые приводят к локальному повышению
расхода (это служило критерием начала неустойчивости).
Вводимые в спецификации тестовой задачи [5] поправки для местного гидравлического
сопротивление на входе и выходе (–1 на выходе и +1 на входе, которые учитывают, соответственно,
расширение и сужение потока) также оказывает заметное влияние на получаемый результат, особенно
для меньших значений местных коэффициентов гидралического сопротивления на выходе. Однако, в
целях соблюдения условий задачи, местное сопротивление на выходе было решено оставить равное
принятому в базовом расчете.
При изменении расчетного количества слоев, функция ведет себя неоднозначно. Возможно, это
связано с точностью определения начала колебаний, для ответа требуются дополнительные
исследования. Для сокращения времени расчета было выбрано количество слоев, равное 91.
Среди поправок на неизотермичность потока для критерия Нуссельта была выбрана поправка
Краснощекова-Протопопова. Данное решение связано с тем, что в других расчетах, касающихся
сверхкритических параметров, эта поправка лучше предсказывала теплоотдачу при течении в круглой
трубе. В таблице 5 приведены формулы расчета для различного типа поправок на неизотермичность
потока для критерий Нуссельта, используемые в программном комплексе ТЕМПА-СК.
№
1
Таблица 5
Список поправок на критерий Нуссельта, используемых в программе ТЕМПА-СК.
Поправка на критерий теплоотдачи
Формула
Кириллов и др. (1990) [8], [7]
⎛ c
Nu/Nu 0 = ⎜ p
⎜c
⎝ pж
Джексон и Фистер (1975) [8], [9]
Nu = 0, 0183Re
2
3
n
0,82
ж
5
Pr
0,5
Джексон (2002) [7], [10]
Краснощеков и Протопопов (1960) [7], [11], [12]
Краснощеков и др. (1967) [7], [13]
⎛ ρ ст ⎞
⎜
⎟
⎝ ρж ⎠
0,3
0,3
Nu = 0, 0183 Re
4
m
⎞ ⎛ ρст ⎞
⎟⎟ ⋅ ⎜
⎟ ⋅ ϕ (K)
⎠ ⎝ ρж ⎠
⎛ ρ ст ⎞ ⎛ cp ⎞
⎟
⎜
⎟ ⎜
⎝ ρ ж ⎠ ⎜⎝ cpж ⎟⎠
Pr
0 ,11
⎛ λж ⎞
⎟⎟
⎜⎜
⎝ λ ст ⎠
⎛μ ⎞
Nu = Nu 0 ⎜⎜ ж ⎟⎟
⎝ μ ст ⎠
⎛ρ ⎞
Nu = Nu 0 ⎜⎜ ст ⎟⎟
⎝ ρж ⎠
0,5
0,82
ж
0,3
−0 , 33
⎛ cp ⎞
⎜
⎟
⎜ cpж ⎟
⎝
⎠
n
0 , 35
,
n
⎛ cp ⎞
⎜
⎟ ,
⎜ cpж ⎟
⎝
⎠
Среди поправок на неизотермичность потока для гидравлического сопротивления трения была
выбрана поправка Попова. В таблице 6 приведены формулы различного типа поправок, используемые в
программе ТЕМПА-СК.
1
Таблица 6
Список поправок на гидравлическое сопротивление, используемых в программе
ТЕМПА-СК.
Поправка на коэффициент гидравлического
Формула
сопротивления
0,4
Кириллов и др. [14], [15]
⎛ρ ⎞
2
Попов [14], [16]:
3
Попов (упрощ.)
4
Тарасова и Леонтьев [14], [17]
5
Михеев [18]
№
ξ / ξ0 = ⎜
ст
⎟
⎝ ρж ⎠
0,74
⎛ ρ ⎞
ξ / ξ0 = ⎜ ⎟ ,
⎝ ρж ⎠
где ρ = ρст + ρ ж .
2
⎛ ρ ст ⎞
⎟
⎝ ρж ⎠
0,74
ξ / ξ0 = ⎜
⎛ μст ⎞
⎟
⎝ μж ⎠
0,22
ξ / ξ0 = ⎜
1
⎛ Pr ⎞ 3
ξ / ξ 0 = ⎜ ст ⎟
⎝ Prж ⎠
После принятия рекомендованных параметров расчетной схемы получаются результаты,
представленные в таблице 7. Дополнительно рассчитаны варианты без учета поправок на значения
местных коэффициентов гидравлического сопротивления.
Таблица 7
Сравнение результатов расчета по доработанной схеме с эталонными результатами.
Вариант
Kout=20
Kout=10
Kout=5
Результаты линейного анализа устойчивости
2,80
3,24
3,75
Базовые значения параметров
2,93
3,53
4,28
Рекомендуемые значения параметров
2,78
3,38
4,11
2,71
3,23
3,87
Рекомендуемые значения параметров без
поправок на значения местных коэффициентов
гидравлического сопротивления (ГП)
6. Заключение
Выполненный анализ чувствительности показал, что наибольше влияние на расчетное значение
границы устойчивости оказывают не параметры расчетной схемы и принятые корреляции для
коэффициента теплоотдачи и коэффициента трения, а параметры алгоритма поиска границы
неустойчивости (скорость повышения мощности), а также неопределенность местных коэффициентов
гидравлического сопротивления.
В ходе работы были выбраны параметры, рекомендованные для расчетов тестовой задачи
МАГАТЭ. Результаты выполненного анализа могут использоваться при разработке расчетных моделей
для анализа гидродинамической устойчивости течения теплоносителя в ТВС ВВЭР-СКД.
7. Список литературы
1.
2.
3.
Ягов П.В., Чуркин А.Н. Программа расчета процессов тепломассопереноса в ТВС активной
зоны реакторов с водой сверхкритического давления ТЕМПА-СК // Сб. труд. конференции
молодых специалистов ОКБ «ГИДРОПРЕСС» 2008. – Подольск, ОКБ «ГИДРОПРЕСС», 2008.
– С.23-32.
Churkin A.N., Yagov P.V., “Computer code TEMPA-SC: Simulation of Thermo-Hydraulic Processes
in the Core of VVER-SCP Reactor”, 4th International Symposium on Supercritical Water-Cooled
Reactors, March 8-11, 2009, Heidelberg, Germany, Paper No. 02,
http://www.hplwr.eu/public/Symposium/Proceedings_01-20.zip.
Ягов П.В., Чуркин А.Н., Щекин И.Г. Испытания программы ТЕМПА-СК // Международная
научно-техническая конференция «Обеспечение безопасности АЭС с ВВЭР», ОКБ
«ГИДРОПРЕСС», 2009.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
Churkin A.N., Yagov P.V., Mokhova O.V. Thermal-Hydraulics of VVER-SCP Core with SinglePass Coolant Flow. Hydroprofiling and Stability // IAEA technical meeting on “Heat transfer,
thermal-hydraulics and system design for super-critical water-cooled reactors”, July 5-8, 2010, Pisa,
Italy. Paper № TM24.
Ambrosini W. Specifications for a Benchmark Exercise on Flow Stability in Heated Channels with
Supercritical Fluids, University of Pisa, Italy, DIMNP RL 1214(2009) Rev. 3, Pisa, March 16th,
2010.
Ambrosini W., Sharabi M. Dimensionless Parameters in Stability Analysis of Heated Channels with
Fluids at Supercritical Pressures, Nuclear Engineering and Design 238 (2008), p.1917–1929.
Кириллов П.Л., Юрьев Ю.С., Бобков В.П. Справочник по теплогидравлическим расчетам
(ядерные реакторы, теплообменники, парогенераторы). М: Энергоатомиздат. 1990.
Pioro I.L., Duffey R.B. Heat Transfer and Hydraulic Resistance at Supercritical Pressures in Power
Engineering Applications. – ASME Press, New York, NY, USA, 2007. – 328 p.
Jackson J.D., Fewster J., 1975. Forced Convection Data for Supercritical Pressure Fluids. HTFS
21540.
Jackson J.D., 2002. Consideration of Heat Transfer Properties of Supercritical Pressure Water in
Connection with the Cooling of Advanced Nuclear Reactors. Proc. of the 13th Pacific Basin Nuclear
Conf., Shenzhen City, China, Oct. 21-25
Краснощеков Е. А., Протопопов В. С., 1959. Теплообмен при сверхкритических параметрах в
потоках углекислого газа и воды в трубах. Теплоэнергетика, No. 12, стр. 26–30.
Краснощеков Е. А., Протопопов В. С., 1960. Теплообмен при сверхкритических параметрах в
потоках углекислого газа и воды в трубах. Теплоэнергетика, No. 10, стр. 94
Краснощеков Е. А., Протопопов В. С., Кураева И. В., 1967 Экспериментальное исследование
теплообмена углекислого газа при сверхкритических параметрах. Доклады второй всесоюзной
конференции тепло- и массопереноса, Минск, Беларусь, Май 1964, Часть 1, стр. 26-35
Pioro I.L., Duffey R.B. Heat Transfer and Hydraulic Resistance at Supercritical Pressures in Power
Engineering Applications. – ASME Press, New York, NY, USA, 2007. – 328 p.
Кириллов П.Л., Юрьев Ю. С., Бобков В.П. Справочник по теплогидравлическим расчетам
(ядерные реакторы, теплообменники, парогенераторы). М: Энергоатомиздат. 1990, Москва,
Россия, стр. 66–67, стр. 130–132.
Попов В. Н., 1967. Теоретический расчет теплообмена и сопротивления трению для
сверхкритического углекислого газа. Доклады второй всесоюзной конференции тепло- и
массопереноса, Минск, Беларусь, Май 1964, Часть 1, стр. 46-56.
Тарасова Н. В. И Леонтьев Н. В., 1968. Гидравлическое сопротивление при течении воды в
обогреваемых трубах при сверхкритических параметрах, (Теплофизика Высоких Температур,
стр. 755–756.) стр. 721-722.
Pioro I.L., Duffey R.B., Tyler J.D., “Hydraulic Resistance of Fluids Flowing in Channels at
Supercritical Pressures (Survey),” Nuclear Engineering and Design, 231, 124, 187-197 (2004).