Решить транспортную задачу методом потенциалов

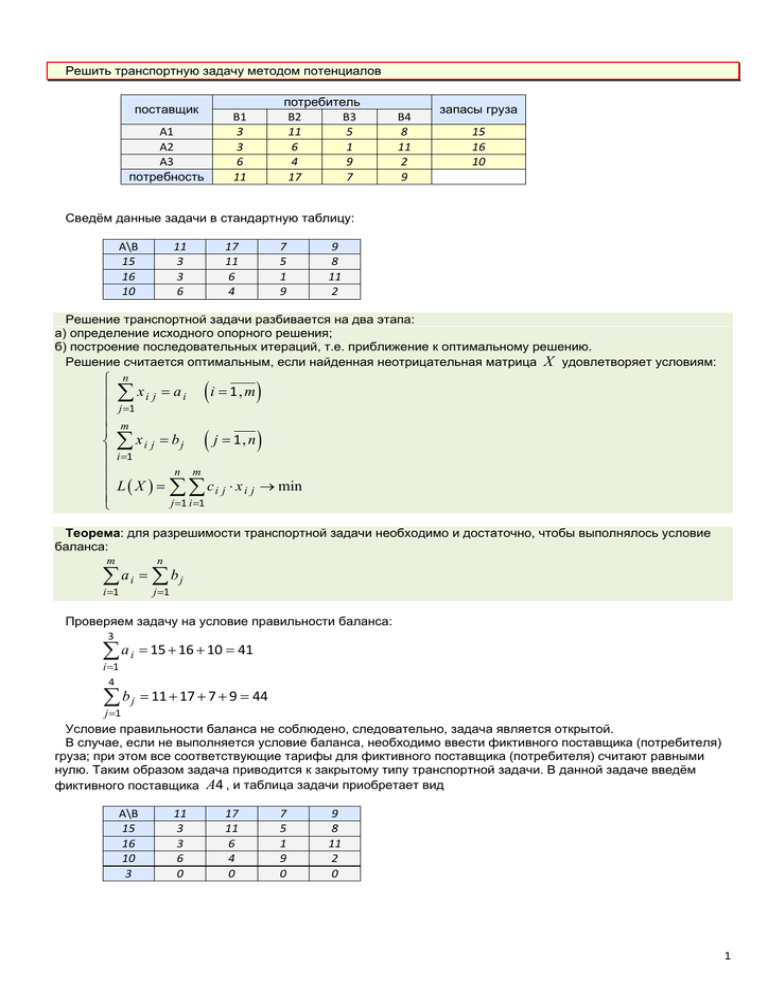
Решить транспортную задачу методом потенциалов
поставщик
потребитель
B2 B3
11 5
6 1
4 9
17 7
B1 3 3 6 11 A1 A2 A3 потребность
B4
8
11
2
9
запасы груза
15
16
10
Сведём данные задачи в стандартную таблицу:
A\B 15 16 10 11 3 3 6 17 11 6
4
7 5 1 9 9
8
11
2
Решение транспортной задачи разбивается на два этапа:
а) определение исходного опорного решения;
б) построение последовательных итераций, т.е. приближение к оптимальному решению.
Решение считается оптимальным, если найденная неотрицательная матрица X удовлетворяет условиям:
⎧ n
i = 1, m
⎪ ∑ xi j = ai
⎪ j =1
⎪ m
⎪
j = 1, n
⎨ ∑ xi j = bj
⎪ i =1
⎪
n m
⎪ L ( X ) = ∑ ∑ c i j ⋅ x i j → min
⎪
j =1 i =1
⎩
(
)
(
)
Теорема: для разрешимости транспортной задачи необходимо и достаточно, чтобы выполнялось условие
баланса:
m
n
i =1
j =1
∑ ai = ∑ bj
Проверяем задачу на условие правильности баланса:
3
∑ a i = 15 + 16 + 10 = 41
i =1
4
∑ b j = 11 + 17 + 7 + 9 = 44
j =1
Условие правильности баланса не соблюдено, следовательно, задача является открытой.
В случае, если не выполняется условие баланса, необходимо ввести фиктивного поставщика (потребителя)
груза; при этом все соответствующие тарифы для фиктивного поставщика (потребителя) считают равными
нулю. Таким образом задача приводится к закрытому типу транспортной задачи. В данной задаче введём
фиктивного поставщика A4 , и таблица задачи приобретает вид
A\B 15 16 10 3 11 3 3 6 0 17 11 6
4
0
7 5 1 9 0 9
8
11
2
0
1 Последовательность дальнейших действий такова:
● составим распределительную (транспортную) таблицу для закрытой задачи,
● строим начальный опорный план,
● вычисляем потенциалы (для занятых поставками клеток) *,
● вычисляем оценки (для незанятых клеток).
Если получится хотя бы одна отрицательная оценка, то план неоптимален, и для клетки с наибольшей (по
модулю) отрицательной оценкой построим цикл пересчёта, тем самым улучшив план. Для нового опорного
плана повторяем все вычисления, начиная с пункта *.
Если же все оценки неотрицательны, то план перевозок оптимален; вычислим его стоимость и выпишем
матрицу перевозок, не включая в неё фиктивного поставщика или фиктивного потребителя, если таковые
были.
№ 3 7 1
2
№ A\B 11 17 7 9 6 15 5 16 4 10 7 3 vj 3
11
3
6
0
3 11
4
6
9
4
1
0
3
11 5
1
7
9
0
6 8
ui 0 ‐5 ‐7 ‐11 11
2
9
0
9 №0 L ( X ) = 3 ⋅ 11 + 11 ⋅ 4 + 6 ⋅ 9 + 1 ⋅ 7 + 4 ⋅ 1 + 2 ⋅ 9 + 0 ⋅ 3 = 160
► Определим начальный план. Начальный план составим методом минимальных тарифов (альтернативный
метод - правило "северо-западного угла").
№ min тариф
поставка
вычёркиваем
1 c 23 = 1 x 23 = 7 j = 3 2 c 34 = 2 x 34 = 9 j =4 3 c 11 = 3 x 11 = 11 j =1 4 c 32 = 4 x 32 = 1 i =3 5 c 22 = 6 x 22 = 9 i =2 6 c 12 = 11 x 12 = 4
i =1
7 c 42 = 0 x 42 = 3 i = 4, j = 2 Фиктивный поставщик с нулевыми тарифами рассматривается в последнюю очередь.
Заметим, что на последнем шаге всегда происходит одновременное освобождение строки и столбца; так что
в благоприятном (невырожденном) случае получается m + n − 1 заполненных клеток таблицы ( m - количество
строк, n - количество столбцов).
Клетки таблицы, в которых записаны поставки, называются базисными, а остальные клетки - свободными.
Полученный план невырожденный ( m + n − 1 = 4 + 4 − 1 = 7 ).
Неотрицательная матрица X , удовлетворяющая условиям задачи, называется планом (или допустимым
планом) задачи. Допустимый план называется оптимальным, если он доставляет минимум целевой функции.
Допустимый план, имеющий не более m + n − 1 отличных от нуля компонентов x i j , называется базисным,
или опорным. Опорный план, имеющий ровно m + n − 1 отличных от нуля компонент, называется
невырожденным, а если число отличных от нуля компонент меньше, чем m + n − 1 , то план называется
вырожденным.
2 Оценим полученный план перевозок методом потенциалов. К строкам и столбцам матрицы затрат
ci j ,
оформленной в виде распределительной таблицы, подберём числа u i и v j так, чтобы u i + v j = c i j для
каждой занятой клетки ( i , j ) . Числа u i и v j называются потенциалами.
Поскольку число занятых клеток равно m + n − 1 , то для однозначного определения потенциалов u i , v j
один из них можно брать произвольно, например, u 1 = 0 (или число, отличное от нуля - неважно).
Потенциалы записываются в дополнительных строке и столбце. Пусть u 1 = 0 , тогда остальные потенциалы
находятся последовательно следующим образом:
u 1 + v 1 = c 11 = 3
→
v1 = 3
u 1 + v 2 = c 12 = 11
→
v 2 = 11
u 2 + v 2 = c 22 = 6
→
u 2 = −5
u 2 + v 3 = c 23 = 1
→
v3 = 6
u 3 + v 2 = c 32 = 4
→
u 3 = −7
u 3 + v 4 = c 34 = 2
→
v4 = 9
u 4 + v 2 = c 42 = 0
→
u 4 = −11
► Проверяем план на оптимальность, вычисляя оценки всех клеток таблицы. Поскольку оценки для занятых
клеток равны нулю, вычисляем оценки для всех незанятых клеток:
Δ13 = c 13 − u 1 − v 3 = 5 − 0 − 6 = −1
<0
Δ14 = c 14 − u 1 − v 4 = 8 − 0 − 9 = −1
<0
Δ21 = c 21 − u 2 − v 1 = 3 − ( −5) − 3 = 5
Δ24 = c 24 − u 2 − v 4 = 11 − ( −5 ) − 9 = 7
Δ31 = c 31 − u 3 − v 1 = 6 − ( −7 ) − 3 = 10
Δ33 = c 33 − u 3 − v 3 = 9 − ( −7 ) − 6 = 10
Δ 41 = c 41 − u 4 − v 1 = 0 − ( −11) − 3 = 8
Δ 43 = c 43 − u 4 − v 3 = 0 − ( −11 ) − 6 = 5
Δ 44 = c 44 − u 4 − v 4 = 0 − ( −11) − 9 = 2
Получены две клетки с отрицательной оценкой:
Δ13 = −1 , Δ14 = −1 .
План неоптимален, будем его улучшать. Но прежде определим стоимость реализации этого плана.
Вычисляем затраты по начальному плану (значение целевой функции):
L ( X ) = 3 ⋅ 11 + 11 ⋅ 4 + 6 ⋅ 9 + 1 ⋅ 7 + 4 ⋅ 1 + 2 ⋅ 9 + 0 ⋅ 3 = 160
Чтобы улучшить план перевозок, имеющий отрицательные оценки, необходимо для свободной клетки
распределительной таблицы, имеющей отрицательную оценку, построить цикл пересчёта (называемый
коротко циклом). Цикл позволяет перераспределить занятые клетки так, чтобы получить новый план перевозок
с меньшими суммарными затратами.
Цикл - это совокупность клеток распределительной таблицы, из которых только одна клетка свободная - та,
для которой строится цикл. Клетки, составляющие цикл, расположены в углах замкнутой ломаной линии,
каждый отрезок которой лежит на одной и той же строке или на одном и том же столбце распределительной
таблицы (т.е. наискось по строкам или столбцам отрезки ломаной не могут располагаться).
Если ломаная линия пересекается в некоторой клетке, то эта клетка не принадлежит циклу.
Теорема. Для каждой свободной клетки распределительной таблицы можно построить цикл, и только один.
Каждой клетке цикла поставим в соответствие знаки + и − ; которые при обходе цикла будут чередоваться.
При этом свободную клетку (начальную клетку цикла) всегда считаем положительной. Величина груза,
перемещаемая с помощью цикла, равна наименьшей из величин, расположенных в отрицательных клетках.
3 ► Для клетки (1 , 3 ) , имеющей отрицательную оценку Δ13 = −1 , построим цикл. Он будет включать в себя
клетки + (1 , 3 ) , - ( 2 , 3 ) , + ( 2 , 2 ) , - ( 1 , 2 ) . Величина груза, перемещаемого по клеткам цикла
λ = min {4 , 7} = 4 . Найденную величину прибавим в положительных клетках цикла и вычтем в
отрицательных клетках цикла. При этом, очевидно, клетка ( 1 , 2 ) станет свободной. Таким образом, получен
новый план перевозок:
A\B 15 16 10 3 vj 11 3
11
3
17 6
0
3 7 11
4−4 = 0
6
9 + 4 = 13
4
1
0
3
5
0+4 = 4
1
7−4 = 3
9
0
10 5 ui 9 8
11
2
9
0
0 ‐4 ‐6 ‐10 8 №1 L ( X ) = 3 ⋅ 11 + 5 ⋅ 4 + 6 ⋅ 13 + 1 ⋅ 3 + 4 ⋅ 1 + 2 ⋅ 9 + 0 ⋅ 3 = 156
Таким образом построена таблица с новым планом, состоящим из старых поставок, не вовлечённых в цикл,
и новых - в вершинах рассмотренного цикла. Клетка (1 , 3 ) теперь занята, а клетка (1 , 2 ) стала свободной.
Произведём перерасчёт потенциалов u i , v j и оценок Δ i j . Пусть u 1 = 0 , тогда
u 1 + v 1 = c 11 = 3
→
v1 = 3
u 1 + v 3 = c 13 = 5
→
v3 = 5
u 2 + v 3 = c 23 = 1
→
u 2 = −4
u 2 + v 2 = c 22 = 6
→
v 2 = 10
u 3 + v 2 = c 32 = 4
→
u 3 = −6
u 3 + v 4 = c 34 = 2
→
v4 = 8
u 4 + v 2 = c 42 = 0
→
u 4 = −10
Вычисляем оценки (для незанятых клеток, поскольку оценки всех занятых клеток - нулевые):
Δ12 = c 12 − u 1 − v 2 = 11 − 0 − 10 = 1
Δ14 = c 14 − u 1 − v 4 = 8 − 0 − 8 = 0
Δ21 = c 21 − u 2 − v 1 = 3 − ( −4 ) − 3 = 4
Δ24 = c 24 − u 2 − v 4 = 11 − ( −4 ) − 8 = 7
Δ31 = c 31 − u 3 − v 1 = 6 − ( −6 ) − 3 = 9
Δ33 = c 33 − u 3 − v 3 = 9 − ( −6 ) − 5 = 10
Δ 41 = c 41 − u 4 − v 1 = 0 − ( −10 ) − 3 = 7
Δ 43 = c 43 − u 4 − v 3 = 0 − ( −10 ) − 5 = 5
Δ 44 = c 44 − u 4 − v 4 = 0 − ( −10 ) − 8 = 2
4 Отрицательных оценок нет, следовательно, найден оптимальный план перевозок груза с матрицей объёмов
перевозок
⎛ 11 0 4 0 ⎞
⎜
⎟
X = ⎜ 0 13 3 0 ⎟
⎜ 0 1 0 9⎟
⎝
⎠
При этом L ( X ) = 3 ⋅ 11 + 5 ⋅ 4 + 6 ⋅ 13 + 1 ⋅ 3 + 4 ⋅ 1 + 2 ⋅ 9 + 0 ⋅ 3 = 156 .
Замечание. Если найден оптимальный план и:
• Если одна или несколько оценок свободных клеток равны нулю, то транспортная задача имеет
альтернативные оптимальные решения.
• И наоборот, если среди оценок свободных клеток нет нулевых, задача имеет единственное решение.
Решение задачи в Mathcad 14:
Получено одно из альтернативных оптимальных решений. Изменив параметры функции Minimize, получим
другое оптимальное решение:
Литература:
1) Лунгу К.Н. "Линейное программирование; руководство к решению задач", 2005, стр. 85;
2) Данко П.Е., Попов А.Г., Кожевникова Т.Я. "Высшая математика в упражнениях и задачах", часть 1, 2003, стр. 288;
3) Алексеев Е.Р., Чеснокова О.В. "Mathcad 12", 2005, стр. 224;
4) Истомин Л.А., Степин В.П. "Математическое программирование", 2003, стр. 19 (решение транспортной задачи методом
потенциалов);
5) Плотников А.Д. "Математическое программирование", 2006, стр. 109 (транспортная задача).
5