Validation & Verification
реклама
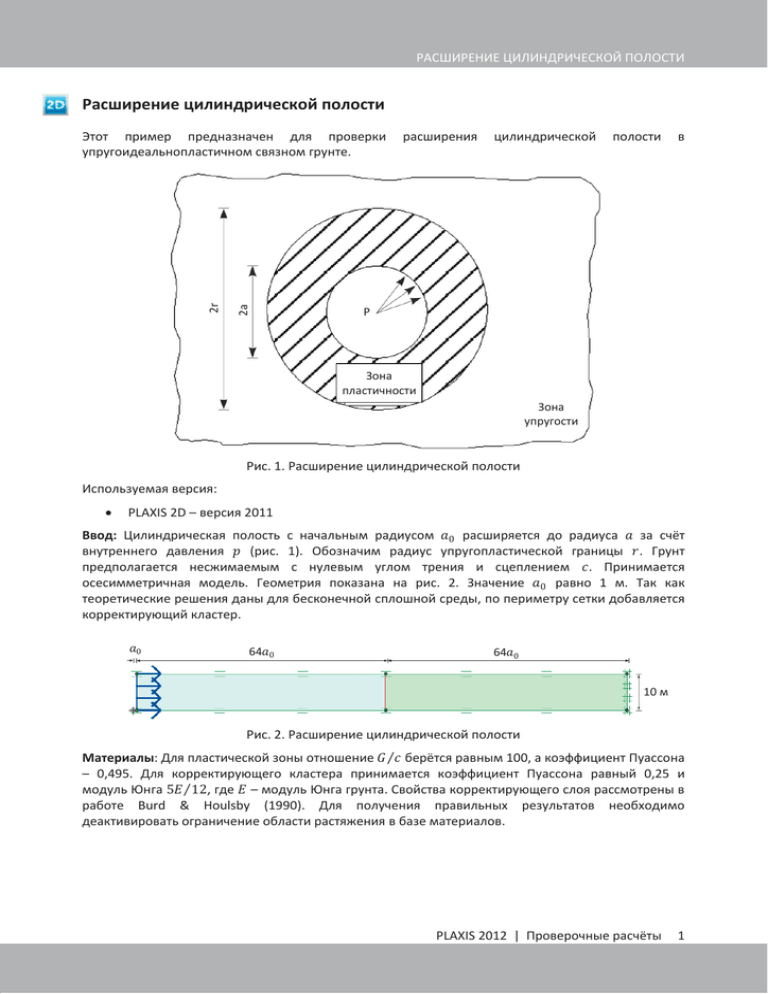
РАСШИРЕНИЕ ЦИЛИНДРИЧЕСКОЙ ПОЛОСТИ Расширение цилиндрической полости 2a 2r Этот пример предназначен для проверки упругоидеальнопластичном связном грунте. расширения цилиндрической полости в P Зона пластичности Зона упругости Рис. 1. Расширение цилиндрической полости Используемая версия: x PLAXIS 2D – версия 2011 Ввод: Цилиндрическая полость с начальным радиусом ܽͲ расширяется до радиуса ܽ за счёт внутреннего давления ( рис. 1). Обозначим радиус упругопластической границы ݎ. Грунт предполагается несжимаемым с нулевым углом трения и сцеплением ܿ. Принимается осесимметричная модель. Геометрия показана на рис. 2. Значение ܽͲ равно 1 м. Так как теоретические решения даны для бесконечной сплошной среды, по периметру сетки добавляется корректирующий кластер. ܽͲ 64ܽͲ 64ܽͲ 10 м Рис. 2. Расширение цилиндрической полости Материалы: Для пластической зоны отношение ܩΤܿ берётся равным 100, а коэффициент Пуассона – 0,495. Для корректирующего кластера принимается коэффициент Пуассона равный 0,25 и модуль Юнга ͷ ܧΤͳʹ, где – ܧмодуль Юнга грунта. Свойства корректирующего слоя рассмотрены в работе Burd & Houlsby (1990). Для получения правильных результатов необходимо деактивировать ограничение области растяжения в базе материалов. PLAXIS 2012 | Проверочные расчёты 1 ПРОВЕРОЧНЫЕ РАСЧЁТЫ Грунт: Модель Мора-Кулона ܩൌ ͳͲͲ кНΤмʹ ܿ ൌ ͳ кНΤмʹ Корректирующий слой: Линейно-упругая модель ܧൌ ͳʹͶǡ кНΤмʹ ߥ ൌ Ͳǡʹͷ ߥ ൌ ͲǡͶͻͷ Сетка: В Global coarseness (Крупность сетки) выбирается опция Coarse (Грубая). Измельчите сетку в точках заданных перемещений при значении Local element size factor (Коэффициент крупности элемента), равном 0,2. Установите коэффициент крупности элемента для других точек равным 2. Окончательная сетка конечных элементов представлена на рис. 3. Рис. 3. Сетка для задачи расширения цилиндрической полости Расчёты: В начальной фазе расчётов создаются нулевые начальные напряжения с использованием процедуры Ͳܭпри σ െ ݐ݄ ݃݅݁ݓܯравным нулю. Расчёт малых деформаций проводится в две фазы. Фаза 1 – пластический расчёт и для Loading input (Ввод нагрузки) выбирается опция Staged construction (Поэтапное строительство). Устанавливается опция Reset displacement to zero (Сбросить перемещения на ноль). Заданные перемещения активируются. Фаза 2 – пластический расчёт и для Loading input) выбирается опция Multipliers (Коэффициенты). Значения полных коэффициентов определены, как показано на рис. 4. Рис. 4. Вкладка Multipliers (Коэффициенты), отображающая значения, присвоенные коэффициентам Аналогично проводится расчёт больших перемещений. Однако для больших перемещений выполняется расчёт Updated mesh (Изменяемая сетка). Вывод: Вычисленные зависимости между давлением в полости и радиальным перемещением приведены на рис. 5. Для того чтобы рассчитать давление в полости по результатам, полученным с помощью программы PLAXIS, необходимо разделить силу, действующую на 1 радиан поверхности полости, на сумму толщины слоя грунта и радиуса полости. 2 Проверочные расчёты | PLAXIS 2012 Приведённое давление в полости ሺܽ െ ܽͲ ሻΤܽͲ РАСШИРЕНИЕ ЦИЛИНДРИЧЕСКОЙ ПОЛОСТИ Малые перемещения Большие перемещения Малые перемещения PLAXIS 2D Большие перемещения PLAXIS 2D Приведённое радиальное перемещение ሺܽ െ ܽͲ ሻΤܽͲ Рис. 5. Соотношения между радиальным перемещением и давлением в полости Проверка: Эта задача изучалась рядом исследователей. Существуют теоретические решения для малых и больших перемещений (см. Sagaseta (1984)). Аналитическое решение может быть получено с помощью следующих зависимостей. Решение для малых перемещений: ܩ ʹ ݎൌ ʹ ൬ ൰ ܽͲ ሺܽെܽͲ ሻ ܿ ൌ ʹܩሺܽെܽ Ͳ ሻ ܽͲ ൌ ܿ െ ʹܿ ܽͲ ݎ для ݎ൏ ܽͲ для ݎ ܽͲ Решение для больших перемещений: ʹݎൌ ͳ ʹ ሺܽ െ ܽͲʹ ሻ ߟʹݎ ൌ ܨܩሺߟሻ ݎ൏ܽ для ߟ ൌ ܨܩሺߟ ݎሻ ʹܿ ቀ ቁ ߟݎ для ݎܽ где ߟʹ ൌ ܽʹ െ ܽͲʹ ܽʹ ߟ ʹݎൌ ͳ െ ቀ ܨሺߟሻ ൌ ߟʹ െܿ ቁ ܩ ߟʹ ߟ Ǥ ǤǤ Ͷ ͻ Как видно, результаты программных расчётов очень хорошо согласуются с аналитическими решениями (рис. 5). PLAXIS 2012 | Проверочные расчёты 3 ПРОВЕРОЧНЫЕ РАСЧЁТЫ Для малых перемещений результат аналитического расчёта дал радиус пластической зоны, равный 28,28 м, а радиус, рассчитанный по PLAXIS 2D, равен 27,96 м. Распределение пластических точек для решения при малых перемещениях представлено на рис. 6. Рис. 6. Итоговые пластические точки в решении при малых перемещениях Для больших перемещений результат аналитического расчета дал радиус пластической зоны, равный 49,11 м, а радиус, рассчитанный по PLAXIS 2D, равен 49,09 м. Распределение пластических точек для решения при больших перемещениях представлено на рис. 7. Рис. 7. Итоговые пластические точки в решении при больших перемещениях 4 Проверочные расчёты | PLAXIS 2012 РАСШИРЕНИЕ ЦИЛИНДРИЧЕСКОЙ ПОЛОСТИ БИБЛИОГРАФИЯ [1] Burd, H.J., Houlsby, G.T. (1990). Analysis cylindrical expansion problems. Int. J. Num. Analys. Mech. Geomech., 14, 351–366. [2] Sagaseta, C. (1984). Personal communication. PLAXIS 2012 | Проверочные расчёты 5 ПРОВЕРОЧНЫЕ РАСЧЁТЫ 6 Проверочные расчёты | PLAXIS 2012