Экономические факторы в модели голосования: пример
реклама

ÏÐÈÊËÀÄÍÀß ÝÊÎÍÎÌÅÒÐÈÊÀ
¹2(14) 2009
À. Â. Çàõàðîâ, Äåàí Ôàíòàööèíè
Ýêîíîìè÷åñêèå ôàêòîðû â ìîäåëè ãîëîñîâàíèÿ:
ïðèìåð Íèäåðëàíäîâ, Âåëèêîáðèòàíèè è Èçðàèëÿ
 äàííîé ñòàòüå ïðîâîäèòñÿ ýêîíîìåòðè÷åñêàÿ îöåíêà ïðîñòðàíñòâåííîé ìîäåëè ãîëîñîâàíèÿ íà ïàðëàìåíòñêèõ âûáîðàõ ñ èñïîëüçîâàíèåì îïðîñíûõ äàííûõ ïî Âåëèêîáðèòàíèè, Íèäåðëàíäàì è Èçðàèëþ. Ïîêàçàíî, ÷òî ïðè ãîëîñîâàíèè áîëåå îáðàçîâàííûå èçáèðàòåëè áîëüøèé âåñ ïðèäàþò ïîëèòè÷åñêèì ïðîãðàììàì ïàðòèé. Âûáîð ìåíåå îáðàçîâàííûõ èçáèðàòåëåé îáóñëîâëåí â ïåðâóþ î÷åðåäü èõ äîõîäîì, ìåñòîì ïðîæèâàíèÿ, îòíîøåíèåì ê ðåëèãèè è ïðî÷èìè ñîöèàëüíî-ýêîíîìè÷åñêèìè ôàêòîðàìè.
 ñëó÷àå Èçðàèëÿ àíàëîãè÷íóþ ðîëü èãðàåò ñòåïåíü ñîáëþäåíèÿ èçáèðàòåëåì ðåëèãèîçíûõ òðàäèöèé: ìåíåå ðåëèãèîçíûå èçáèðàòåëè ïðèäàþò áîëüøèé âåñ ïîëèòè÷åñêèì
ïðîãðàììàì ïàðòèé.
Ââåäåíèå
îãëàñíî òåîðèè, ïðåäëîæåííîé Ý. Äàóíñîì â ðàáîòå «Ýêîíîìè÷åñêàÿ òåîðèÿ äåìîêðàòèè», âî âðåìÿ âûáîðîâ èçáèðàòåëü ãîëîñóåò çà òó ïàðòèþ, ÷üÿ ïîëèòè÷åñêàÿ ïðîãðàììà
íàèáîëåå òî÷íî ñîîòâåòñòâóåò åãî ïðåäïî÷òåíèÿì. Ýòî ïðåäïîëîæåíèå ëåæèò â îñíîâå
âñåõ òåîðåòèêî-èãðîâûõ ìîäåëåé ïîëèòè÷åñêîé êîíêóðåíöèè è íåîäíîêðàòíî ïîäâåðãàëîñü
ýìïèðè÷åñêîé ïðîâåðêå. Äàííûé âîïðîñ áûë èññëåäîâàí â îñíîâîïîëàãàþùåé ñòàòüå Ê. Ïóëà è Ã. Ðîçåíòàëÿ [Poole and Rosenthal (1984)], â ðàáîòå Ì. Àëâàðåçà è Äæ. Íýãëåðà [Alvarez and
Nagler (2000)], à òàêæå â ðàáîòàõ Í. Ñêîôèëüäà [Schofield (2007)], Ê. Êóèíà, Ý. Ìàðòèíà è Ý. Óèíôîðäà [Quinn, Martin and Whitford [1999]), Äæ. Àäàìñà, Äæ. Äîó è Ñ. Ìåððèëà [Adams, Dow and
Merrill (2006)] è äð. Àíàëèç ïðîñòðàíñòâåííîé ìîäåëè íà îñíîâå îòå÷åñòâåííûõ äàííûõ, ñîáðàííûõ â 2007 ã. ïåðåä âûáîðàìè â Ãîñóäàðñòâåííóþ Äóìó, áûë ïðîäåëàí àâòîðîì [Çàõàðîâ
(2008)].
 îñíîâå âñåõ ïåðå÷èñëåííûõ âûøå ýìïèðè÷åñêèõ èññëåäîâàíèé ëåæèò òàê íàçûâàåìàÿ âåðîÿòíîñòíàÿ ìîäåëü ãîëîñîâàíèÿ, ñîãëàñíî êîòîðîé âûáîð èçáèðàòåëÿ ÿâëÿåòñÿ ñëó÷àéíîé âåëè÷èíîé. Ïðè ýòîì âåðîÿòíîñòü òîãî, ÷òî èçáèðàòåëü ïðîãîëîñóåò çà ïîëèòè÷åñêóþ ïàðòèþ, çàâèñèò
îò ñòåïåíè ñîîòâåòñòâèÿ ïîëèòè÷åñêîé ïðîãðàììû ïàðòèè âçãëÿäàì èçáèðàòåëÿ, à òàêæå îò ñîöèàëüíî-äåìîãðàôè÷åñêèõ õàðàêòåðèñòèê èçáèðàòåëÿ. Ïðè ðàçëè÷íûõ ïðåäïîëîæåíèÿõ îòíîñèòåëüíî ôóíêöèè ïîëåçíîñòè èçáèðàòåëÿ ìîæíî îöåíèòü ïàðàìåòðû ýòîé ôóíêöèè, èñïîëüçóÿ îïðîñíûå äàííûå è ïðèìåíÿÿ ìîäåëü ìíîæåñòâåííîãî (èëè áèíàðíîãî) âûáîðà.
Âñå ðàáîòû — íà÷èíàÿ ñ ðàáîòû Ïóëà è Ðîçåíòàëÿ [Poole and Rosenthal (1984)], â êîòîðîé
èñïîëüçîâàëèñü äàííûå ïðåçèäåíòñêèõ âûáîðîâ â ÑØÀ, ïîäòâåðæäàþò ãèïîòåçó î òîì, ÷òî
èçáèðàòåëè ñêëîííû ïîääåðæèâàòü ïàðòèè è êàíäèäàòîâ ñ áîëåå áëèçêèìè ïîëèòè÷åñêèìè
ïðîãðàììàìè èëè èäåîëîãè÷åñêèìè ïîçèöèÿìè. Îòìå÷àåòñÿ òàêæå âàæíîñòü òàêèõ ôàêòîðîâ,
êàê ïîïóëÿðíîñòü, ðåïóòàöèÿ è ò. ï. Ñîâîêóïíîñòü äàííûõ ôàêòîðîâ íàçûâàåòñÿ âàëåíòíî-
Ñ
57
R Îáùåñòâî
ÏÐÈÊËÀÄÍÀß ÝÊÎÍÎÌÅÒÐÈÊÀ
Ýêîíîìè÷åñêèå ôàêòîðû â ìîäåëè ãîëîñîâàíèÿ: ïðèìåð Íèäåðëàíäîâ, Âåëèêîáðèòàíèè è Èçðàèëÿ
¹2(14) 2009
ñòüþ êàíäèäàòà èëè ïàðòèè [Stokes (1963)]. Â ðÿäå ðàáîò — [Quinn, Martin et al. (1999)] è [Schofield, Quinn, Martin, and Whitford (1998)] — áûëî ïîêàçàíî, ÷òî âàëåíòíîñòü, ïðèïèñûâàåìàÿ
ïàðòèè èçáèðàòåëåì, çàâèñèò îò åãî ñîöèàëüíî-äåìîãðàôè÷åñêèõ õàðàêòåðèñòèê.
Ïî ðåçóëüòàòàì îöåíêè ïðîñòðàíñòâåííîé ìîäåëè ãîëîñîâàíèÿ íà îñíîâå îïðîñíûõ äàííûõ ìîæíî ïðîâåðÿòü ðàçëè÷íûå ïðåäïîëîæåíèÿ îòíîñèòåëüíî ðàöèîíàëüíîñòè êàíäèäàòîâ èëè ïîëèòè÷åñêèõ ïàðòèé.  ÷àñòíîñòè, ìîæíî ïðîâåðèòü, íàñêîëüêî íàáëþäàåìûå ïîçèöèè ïîëèòè÷åñêèõ àãåíòîâ ñîîòâåòñòâóþò ðàâíîâåñèþ Íýøà ïðè íàáëþäàåìîì ýëåêòîðàòå.
Ýòî ìîæíî ñäåëàòü äâóìÿ ñïîñîáàìè. Âî-ïåðâûõ, ìîæíî íàéòè ðàâíîâåñèå Íýøà ÷èñëåííûìè
ìåòîäàìè. Âî-âòîðûõ, â ðÿäå ðàáîò — [Hinich (1977)], [Lin, Enelow and Dorussen (1999)],
[Schofield (2007)], [Banks and Duggan (2004)], [McKelvey and Patty (2006)] — ïîêàçàíî, ÷òî â âåðîÿòíîñòíîé ìîäåëè ãîëîñîâàíèÿ óñëîâèÿ ïåðâîãî ïîðÿäêà ìàêñèìèçàöèè âûèãðûøà êàíäèäàòîâ óäîâëåòâîðÿþòñÿ, åñëè âñå ïîçèöèè êàíäèäàòîâ ñîâïàäàþò.  ýòîì ñëó÷àå ìîæíî
ïðîâåðèòü, óäîâëåòâîðÿþòñÿ ëè óñëîâèÿ âòîðîãî ïîðÿäêà ìàêñèìèçàöèè âûèãðûøà êàíäèäàòîâ.
Êóèíí è Ìàðòèí [Quinn and Martin (2002)], èññëåäóÿ âûáîðû 1989 ã. â Íèäåðëàíäàõ, ïîêàçàëè, ÷òî ðàâíîâåñèå Íýøà è íàáëþäàåìîå ðàâíîâåñèå íå ñîâïàäàþò. Ïî èõ ìíåíèþ, äàííîå ðàñõîæäåíèå ìîæíî îáúÿñíèòü ñòðàòåãè÷åñêèì ïîâåäåíèåì ïîëèòè÷åñêèõ ïàðòèé, ìàêñèìèçèðóþùèì âåðîÿòíîñòü âõîæäåíèÿ â ïðàâÿùóþ êîàëèöèþ ïîñëå âûáîðîâ.  ðàáîòàõ
[Schofield, Sened and Nixon (1998)], [Schofield and Sened (2005)] è [Schofield (2007)] äëÿ âûáîðîâ 1992 è 1996 ãã. â Èçðàèëå óòâåðæäàåòñÿ, ÷òî ðàñõîæäåíèå ÿâëÿåòñÿ ñëåäñòâèåì äåéñòâèÿ
ïîëèòè÷åñêèõ àêòèâèñòîâ, áîëåå àêòèâíî ïîääåðæèâàþùèõ ïîëèòè÷åñêèå ïàðòèè, èìåþùèå
áëèçêèå ê íèì èäåîëîãè÷åñêèå ïîçèöèè. Ñóùåñòâóþò òàêæå íåäàâíèå ðàáîòû Ñêîôèëüäà è Êàòàéôå [Schofield and Cataife (2007)] ïî âûáîðàì 1989 è 1995 ãã. â Àðãåíòèíå, Ñêîôèëüäà è Îçäåìèðà [Schofield and Ozdemir (2008)] ïî âûáîðàì 1999 è 2002 ãã. â Òóðöèè.
Äðóãîé ñïîñîá îáúÿñíèòü íàáëþäàåìîå ðàñõîæäåíèå â ïîëèòè÷åñêèõ ïðîãðàììàõ ïàðòèé
è êàíäèäàòîâ — ââåñòè àëüòåðíàòèâíûå ïðåäïîëîæåíèÿ îòíîñèòåëüíî ïðåäïî÷òåíèé èçáèðàòåëåé. Ðàáèíîâè÷ è Ìàêäîíàëüä [Rabinovitz and MacDonald (1989)], Èâåðñåí [Iversen (1994)],
Àäàìñ è Ìåððèë [Adams and Merrill (1999)], Ìåððèë è Ãðîôìàí [Merrill and Grofman (1999)]
ïðåäëàãàþò òàê íàçûâàåìóþ òåîðèþ íàïðàâëåííîãî ãîëîñîâàíèÿ, ñîãëàñíî êîòîðîé ñóùåñòâóþò èçáèðàòåëè, ïðåäïî÷èòàþùèå ëåâûå èëè ïðàâûå ïàðòèè, è èçáèðàòåëü çàèíòåðåñîâàí
íå òîëüêî â òîì, íàñêîëüêî ïîëèòè÷åñêàÿ ïðîãðàììà ïàðòèè ñîîòâåòñòâóåò åãî ïðåäïî÷òåíèÿì, íî è â òîì, íàñêîëüêî ëåâîé èëè ïðàâîé îíà ÿâëÿåòñÿ. Àäàìñ, Äîó è Ìåððèë [Adams, Dow,
and Merrill (2006)], Òåðíåð è Åéìàí [Thurner and Eymann (2000)], Ïëåéí è Ãåðøòåíñîí [Plane
and Gershtenson (2004)] è Ïåðåñ [Peress (2005)] ñ÷èòàþò, ÷òî îäíèì èç èñòî÷íèêîâ ðàñõîæäåíèÿ ÿâëÿåòñÿ íåÿâêà èçáèðàòåëåé. Ñîãëàñíî Àëüâàðåñó è Íýãëåðó [Alvarez and Nagler (2000)],
èçáèðàòåëü â Âåëèêîáðèòàíèè ìîæåò ãîëîñîâàòü ñòðàòåãè÷åñêè, èñïîëüçóÿ ñâîé ãîëîñ äëÿ òîãî, ÷òîáû íàêàçàòü ïàðòèþ, êîòîðàÿ ìåíüøå âñåãî åìó íðàâèòñÿ.
Âîïðîñ î òîì, íàñêîëüêî ïîëèòè÷åñêèå ïðîãðàììû ïàðòèé âàæíû äëÿ ðàçíûõ èçáèðàòåëåé, äîñòàòî÷íî ðåäêî ïîäíèìàëñÿ â ñîâðåìåííîé ëèòåðàòóðå. Íåêîòîðûå ìîäåëè — òàêèå,
êàê â ðàáîòå Òåðíåðà è Åéìàíà [Thurner and Eymann (2000)] — ïîçâîëÿþò ðàçíûì ïîëèòè÷åñêèì âîïðîñàì ïðèäàâàòü ðàçíîå çíà÷åíèå. Îäíàêî â áîëüøèíñòâå ìîäåëåé ïðåäïîëàãàëîñü, ÷òî âàæíîñòü êàæäîãî âîïðîñà áóäåò îäèíàêîâîé äëÿ âñåõ èçáèðàòåëåé. Âîçìîæíîñòü
ñóùåñòâîâàíèÿ áîëåå îáùåé ìîäåëè áûëà óêàçàíà â ðàáîòå Ñêîôèëüäà è Ñåíåäà [Schofield
and Sened (2006)].
58
Îáùåñòâî R
ÏÐÈÊËÀÄÍÀß ÝÊÎÍÎÌÅÒÐÈÊÀ
Õýëëâèã [Hellwig (2008a)] èññëåäîâàë ýëåêòîðàëüíîå ïîâåäåíèå â 16 ñòðàíàõ Çàïàäíîé Åâðîïû è ïîêàçàë, ÷òî íåêîòîðûå ãðóïïû èçáèðàòåëåé óäåëÿþò áîëüøåå âíèìàíèå îðèåíòàöèè
ïîëèòè÷åñêèõ ïðîãðàìì ïàðòèé ïî øêàëå «ëåâî—ïðàâî».  ÷àñòíîñòè, ê òàêèì èçáèðàòåëÿì
îòíîñÿòñÿ çàíÿòûå â ïðîèçâîäñòâå íåòîðãóåìûõ òîâàðîâ. Äëÿ òåõ, êòî çàíÿò â ïðîèçâîäñòâå
òîðãóåìûõ òîâàðîâ èëè â ïðîèçâîäñòâå óñëóã, «ëåâèçíà» èëè «ïðàâèçíà» ïîëèòè÷åñêîé ïðîãðàììû ïàðòèè íå òàê âàæíà.  ýòîé è ïîñëåäóþùåé ðàáîòàõ [Hellwig (2008b)] óêàçàíî, ÷òî
âëèÿíèå ïîëèòè÷åñêèõ ýëèò åâðîïåéñêèõ ñòðàí íà ãëîáàëèçîâàííûå ñåêòîðà ýêîíîìèêè îãðàíè÷åíî. Òàêèì îáðàçîì, èçáèðàòåëåé, çàíÿòûõ â ýòèõ îáëàñòÿõ, ïîëèòè÷åñêèå ïðîãðàììû
ïàðòèé èíòåðåñóþò íå òàê ñèëüíî.
 äàííîé ñòàòüå áóäåò èññëåäîâàíà ìîäåëü ìíîæåñòâåííîãî âûáîðà, îñíîâàííàÿ íà òðåõ
íàáîðàõ äàííûõ: Íèäåðëàíäû â 1977 ã., Âåëèêîáðèòàíèÿ â 1987 ã., Èçðàèëü â 1996 ã. Ïðåäïîëàãàåì, ÷òî ñòåïåíü âëèÿíèÿ ïîëèòè÷åñêèõ ïðîãðàìì ïàðòèé íà âûáîð èçáèðàòåëÿ çàâèñèò
îò åãî ñîöèàëüíî-äåìîãðàôè÷åñêèõ õàðàêòåðèñòèê.  îòëè÷èå îò ïðîöèòèðîâàííûõ ðàáîò
ïðåäïîëîæèì, ÷òî èçáèðàòåëü ìîæåò ïðèäàâàòü ðàçíûå âåñà ðàçëè÷íûì àñïåêòàì ïîëèòè÷åñêèõ ïðîãðàìì ïàðòèé.
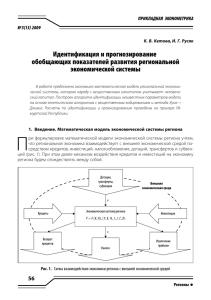
Ðàññìîòðèì ïðèìåð (ðèñ. 1). Äîïóñòèì, èçáèðàòåëåé èíòåðåñóþò äâà ïóíêòà â ïðîãðàììå êàæäîé ïàðòèè: ïîçèöèÿ ïî ýêîíîìè÷åñêîé ïîëèòèêå (ïðàâàÿ ïîçèöèÿ îçíà÷àåò ìåíüøóþ ñòåïåíü
âìåøàòåëüñòâà ãîñóäàðñòâà â ýêîíîìèêó) è ïîçèöèÿ ïî ñîöèàëüíîé ïîëèòèêå (ëèáåðàëüíàÿ ïîçèöèÿ îòðàæàåò ïðèîðèòåò ëè÷íûõ ñâîáîä ãðàæäàí íàä îáùåñòâåííûìè èíòåðåñàìè). Íà ðèñóíêå èçîáðàæåíû ïðåäïî÷òåíèÿ òðåõ èçáèðàòåëåé. Äëÿ êàæäîãî èçáèðàòåëÿ ïîêàçàíû åãî íàèëó÷øàÿ àëüòåðíàòèâà (ò. å. êîìáèíàöèÿ ýêîíîìè÷åñêîé è ñîöèàëüíîé ïîëèòèêè, êîòîðóþ îí
ïðåäïî÷òåò ëþáîé äðóãîé) è îäíà èç êðèâûõ áåçðàçëè÷èÿ.
Ðèñ. 1. Ïðèìåð ðàçëè÷íûõ ïðåäïî÷òåíèé èçáèðàòåëåé
Èçáèðàòåëü A ïðåäïî÷èòàåò ïðàâóþ ýêîíîìè÷åñêóþ è êîíñåðâàòèâíóþ ñîöèàëüíóþ ïîëèòèêó. Ïðè ýòîì îáà àñïåêòà ïîëèòè÷åñêèõ ïëàòôîðì ïàðòèé îäèíàêîâî âàæíû äëÿ äàííîãî èçáèðàòåëÿ. Ïîñëåäíåå óòâåðæäåíèå íå ÿâëÿåòñÿ âåðíûì äëÿ èçáèðàòåëåé B è C. Äëÿ èçáèðàòåëÿ B ýêîíîìè÷åñêàÿ ïîëèòèêà íàìíîãî âàæíåå ñîöèàëüíîé. Ðåøàÿ çàäà÷ó âûáîðà ìåæäó ïîëèòè÷åñêèìè ïàðòèÿìè, òàêîé èçáèðàòåëü îðèåíòèðóåòñÿ â ïåðâóþ î÷åðåäü íà
ïîçèöèþ ïàðòèé ïî ýêîíîìè÷åñêîé ïîëèòèêå. Äëÿ èçáèðàòåëÿ C áîëåå âàæíà ñîöèàëüíàÿ
ïîëèòèêà.
59
R Îáùåñòâî
À. Â. Çàõàðîâ, Äåàí Ôàíòàööèíè
¹2(14) 2009
ÏÐÈÊËÀÄÍÀß ÝÊÎÍÎÌÅÒÐÈÊÀ
¹2(14) 2009
 áîëüøèíñòâå èññëåäîâàíèé (ñì. [Alvarez and Nagler (2000)], [Quinn, Martin, and Whitford
(1999)], [Schofield (2007)] è äðóãèå ðàáîòû) ïðåäïîëàãàëîñü, ÷òî âñå èçìåðåíèÿ ïîëèòè÷åñêèõ
ïðîãðàìì ïàðòèé îäèíàêîâî âàæíû äëÿ èçáèðàòåëåé (ò. å. êðèâûå áåçðàçëè÷èÿ èçáèðàòåëåé ÿâëÿþòñÿ îêðóæíîñòÿìè, êàê ó èçáèðàòåëÿ A íà ðèñ. 1).
Èíûìè ñëîâàìè, ïðîñòðàíñòâåííàÿ ìåòðèêà ïîëèòè÷åñêèõ ïðåäïî÷òåíèé èçáèðàòåëåé ÿâëÿåòñÿ ñòàíäàðòíîé åâêëèäîâîé. Ýòî ïðåäïîëîæåíèå ñîîòâåòñòâóåò ñëåäóþùåé ôóíêöèè ïîëåçíîñòè èçáèðàòåëÿ:
Ýêîíîìè÷åñêèå ôàêòîðû â ìîäåëè ãîëîñîâàíèÿ: ïðèìåð Íèäåðëàíäîâ, Âåëèêîáðèòàíèè è Èçðàèëÿ
u ij = a j + g Tj x i - b| y j - v i | 2 + e ij ,
(1)
ãäå u ij — ïîëåçíîñòü, êîòîðóþ èçáèðàòåëü i Î {1, K , N} ïðèïèñûâàåò ïàðòèè j Î {1, K , M};
a j — ïàðàìåòð, îòðàæàþùèé ïðèâëåêàòåëüíîñòü ïàðòèè j;
g j Î Â L — âåêòîð ïàðàìåòðîâ, êîòîðûå ïîêàçûâàþò, êàê ñîöèàëüíî-äåìîãðàôè÷åñêèå õàðàêòåðèñòèêè èçáèðàòåëÿ âëèÿþò íà ïðèâëåêàòåëüíîñòü äëÿ íåãî ïàðòèÿ j;
x i — âåêòîð ñîöèàëüíî-äåìîãðàôè÷åñêèõ õàðàêòåðèñòèê èçáèðàòåëÿ i (òàêèõ, êàê îáðàçîâàíèå èëè äîõîä);
y j Î Â K — ïîëèòè÷åñêàÿ ïðîãðàììà ïàðòèè j;
v i Î Â K — ïîëèòè÷åñêàÿ ïðîãðàììà, êîòîðóþ èçáèðàòåëü i ñ÷èòàåò íàèëó÷øåé;
b — ïàðàìåòð, îòðàæàþùèé òî, íàñêîëüêî ñèëüíî íà âûáîð èçáèðàòåëåé âëèÿþò ïîëèòè÷åñêèå ïðîãðàììû ïàðòèé;
|×| — åâêëèäîâà ïðîñòðàíñòâåííàÿ ìåòðèêà;
e ij — ñëó÷àéíàÿ îøèáêà;
T — ñèìâîë òðàíñïîíèðîâàíèÿ.
 çàâèñèìîñòè îò ðàçëè÷íûõ ïðåäïîëîæåíèé îòíîñèòåëüíî ðàñïðåäåëåíèÿ âåëè÷èí e ij
íà îñíîâå ôóíêöèè ïîëåçíîñòè (1) â ðàçíûõ ðàáîòàõ îöåíèâàëèñü ëîãèò- èëè ïðîáèò-ìîäåëè
ìíîæåñòâåííîãî âûáîðà.
Âåëè÷èíû y j , v i ïðåäïîëàãàëèñü ëèáî îäíîìåðíûìè, ëèáî äâóìåðíûìè. Ïåðâûé ñëó÷àé
áîëåå õàðàêòåðåí äëÿ ÑØÀ, âòîðîé — äëÿ ñòðàí Çàïàäíîé Åâðîïû. Ïî÷òè âñå èññëåäîâàíèÿ
óêàçûâàëè íà çíà÷èìîñòü êîýôôèöèåíòà b.
Ôóíêöèÿ ïîëåçíîñòè (1) íå îòðàæàåò íåêîòîðûõ åñòåñòâåííûõ ïðåäïîëîæåíèé îòíîñèòåëüíî ýëåêòîðàëüíîãî ïîâåäåíèÿ èçáèðàòåëåé. Âî-ïåðâûõ, ðàçíûå èçáèðàòåëè ìîãóò ïîðàçíîìó îöåíèâàòü âàæíîñòü ðàçëè÷íûõ àñïåêòîâ ïîëèòè÷åñêèõ ïðîãðàìì ïàðòèé (êàê, íàïðèìåð, èçáèðàòåëè B è C íà ðèñ. 1. Ïðè÷åì âàæíîñòü òîãî èëè èíîãî àñïåêòà ìîæåò îïðåäåëÿòüñÿ ñîöèàëüíî-äåìîãðàôè÷åñêèìè õàðàêòåðèñòèêàìè èçáèðàòåëÿ.
Âî-âòîðûõ, äëÿ íåêîòîðîé ãðóïïû èçáèðàòåëåé (ñêàæåì, äëÿ áîëåå îáðàçîâàííûõ èëè áîëåå èíôîðìèðîâàííûõ) ìîãóò áûòü âàæíû îáà èçìåðåíèÿ ïîëèòè÷åñêîé ïðîãðàììû. Ìåíåå
îáðàçîâàííûé èçáèðàòåëü, êîòîðûé íå ñëåäèò çà ïîëèòè÷åñêîé îáñòàíîâêîé, ìîæåò ïðîñòî
íå îáðàùàòü âíèìàíèÿ íà ïîëèòè÷åñêèå ïðîãðàììû ïàðòèé. Âûáîð òàêîãî èçáèðàòåëÿ
â áîëüøåé ìåðå ìîæåò áûòü îáóñëîâëåí åãî ñîöèàëüíî-äåìîãðàôè÷åñêèìè õàðàêòåðèñòèêàìè (íàïðèìåð, áîëåå ðåëèãèîçíûé èçáèðàòåëü ïðîãîëîñóåò çà ïàðòèþ, êîòîðàÿ ïîçèöèîíèðóåò ñåáÿ êàê «õðèñòèàíñêàÿ»). Òàêîé èçáèðàòåëü òàêæå áóäåò îòäàâàòü ïðåäïî÷òåíèå ïàðòèÿì ñ áîëüøèì àäìèíèñòðàòèâíûì èëè ôèíàíñîâûì ðåñóðñîì. Èñõîäÿ èç ýòèõ ïðåäïîëîæåíèé
ñëåäóåò ñôîðìóëèðîâàòü áîëåå îáùóþ ìîäåëü â îòëè÷èå îò ìîäåëè (1).
60
Îáùåñòâî R
ÏÐÈÊËÀÄÍÀß ÝÊÎÍÎÌÅÒÐÈÊÀ
1. Äàííûå
Èñïîëüçóåì äâà èñòî÷íèêà èñõîäíûõ äàííûõ. Ïåðâûé — îïðîñ íàñåëåíèÿ Åâðîáàðîìåòð1
(Eurobarometer), ïðîâåäåííûé â Íèäåðëàíäàõ è Âåëèêîáðèòàíèè â 1978 ã., è îïðîñ åâðîïåéñêèõ ïàðòèéíûõ ýëèò ñðåäíåãî óðîâíÿ (EPPMLE — European Political Parties’ Middle Level Elites),
ïðîâåäåííûé òàì æå è â òîì æå ãîäó. Ñîöèîëîãè÷åñêèé îïðîñ Åâðîáàðîìåòð ïðîâîäèòñÿ
äâàæäû â ãîä â ñòðàíàõ Åâðîñîþçà íà÷èíàÿ ñ 1971 ã.
Ñðåäè âîïðîñîâ, çàäàâàåìûõ â õîäå îïðîñà Åâðîáàðîìåòð, íàñ èíòåðåñîâàëè 5 âîïðîñîâ,
ôèêñèðóþùèõ ñîöèàëüíî-ýêîíîìè÷åñêèé ñòàòóñ ðåñïîíäåíòà, 7 âîïðîñîâ, îïðåäåëÿþùèõ
åãî ïîëèòè÷åñêèå ïðåäïî÷òåíèÿ, è âîïðîñ î íàìåðåíèè ðåñïîíäåíòà ãîëîñîâàòü íà ïðåäñòîÿùèõ ïàðëàìåíòñêèõ âûáîðàõ. Ïî îòâåòàì íà ïåðâûå 5 âîïðîñîâ ìû îïðåäåëèëè ïåðåìåííûå manlab (1 — åñëè ðåñïîíäåíò çàíèìàåòñÿ ôèçè÷åñêèì òðóäîì, 0 — â îáðàòíîì ñëó÷àå), income (äîõîä ïî øêàëå — îò 0 äî 12), relig (ñòåïåíü ðåëèãèîçíîñòè ðåñïîíäåíòà — îò 0
äî 4), educ (êîëè÷åñòâî ëåò îáðàçîâàíèÿ ïîñëå ñðåäíåé øêîëû — îò 1 äî 9), stown (ðàçìåð
íàñåëåííîãî ïóíêòà, â êîòîðîì ïðîæèâàåò ðåñïîíäåíò, — îò 0 äî 3).
Âòîðîé íàáîð âîïðîñîâ âûÿñíÿåò îòíîøåíèå ðåñïîíäåíòà ê îñíîâíûì àêòóàëüíûì ïîëèòè÷åñêèì âîïðîñàì, âêëþ÷àÿ ãîñóäàðñòâåííîå ðåãóëèðîâàíèå êðóïíûõ ìåæíàöèîíàëüíûõ
êîðïîðàöèé, ïðàâî æåíùèí íà àáîðò, íåîáõîäèìîñòü äîïîëíèòåëüíûõ ñèëîâûõ ìåð ïî áîðüáå ñ ìåæäóíàðîäíûì òåððîðèçìîì, ðàçâèòèå ÿäåðíîé ýíåðãåòèêè, ðàñøèðåíèå äîëè ãîñóäàðñòâà â ñîáñòâåííîñòè ïóáëè÷íûõ êîìïàíèé, äîïîëíèòåëüíûå ìåðû ïî çàùèòå îêðóæàþùåé ñðåäû, ïåðåðàñïðåäåëåíèå äîõîäà ìåæäó èìóùèìè è íåèìóùèìè ñëîÿìè íàñåëåíèÿ. Îòâåò íà êàæäûé âîïðîñ ðàñïîëàãàåòñÿ ïî øêàëå îò 1 äî 7. Äâóìåðíûå îöåíêè ïîëèòè÷åñêèõ
ïðåäïî÷òåíèé ðåñïîíäåíòîâ ïîëó÷åíû ñ èñïîëüçîâàíèåì ôàêòîðíîãî àíàëèçà â ðàáîòå Êóèííà, Ìàðòèíà è Óèòôîðäà [Quinn, Martin and Whitford (1999)]. Ýòè îöåíêè èñïîëüçóþòñÿ
è â äàííîé ñòàòüå.
Íà îñíîâå ðåçóëüòàòîâ ôàêòîðíîãî àíàëèçà ìîæíî äàòü ñëåäóþùóþ èíòåðïðåòàöèþ ïîëó÷åííûõ îöåíîê ïîëèòè÷åñêèõ ïðåäïî÷òåíèé ðåñïîíäåíòîâ. Ïåðâîå èçìåðåíèå (èëè ïåðâûé
ôàêòîð ïðåäïî÷òåíèé) òðàêòóåòñÿ êàê ñòàíäàðòíîå ïîëîæåíèå èçáèðàòåëÿ ïî øêàëå «ëåâî—ïðàâî». Âòîðîå èçìåðåíèå (ôàêòîð) — êàê îòíîøåíèå èçáèðàòåëÿ ê óðîâíþ ïîëèòè÷åñêèõ è ãðàæäàíñêèõ ñâîáîä â îáùåñòâå. Èçáèðàòåëü ñ âûñîêèì çíà÷åíèåì ýòîãî ôàêòîðà áóäåò ïîääåðæèâàòü ïðàâî æåíùèí íà àáîðò, ÿâëÿòüñÿ ïðîòèâíèêîì æåñòêèõ ìåð ïî áîðüáå
ñ òåððîðèçìîì è ÿâëÿòüñÿ ñòîðîííèêîì ïåðåðàñïðåäåëåíèÿ äîõîäîâ ìåæäó áîãàòûìè è áåäíûìè.
Âòîðîé èñòî÷íèê äàííûõ, èñïîëüçóåìûé íàìè, — îïðîñ îáùåñòâåííîãî ìíåíèÿ, ïðîâåäåííûé â Èçðàèëå ïåðåä ïàðëàìåíòñêèìè âûáîðàìè 1996 ã. [Arian and Shamir (1999)]. Äâóìåðíûå îöåíêè ïîëèòè÷åñêèõ ïðåäïî÷òåíèé áûëè ïîëó÷åíû èç èñõîäíûõ îïðîñíûõ äàííûõ ñ èñïîëüçîâàíèåì ôàêòîðíûõ âåñîâ èç ðàáîòû Ñêîôèëüäà è Ñåíåäà [Schofield and Sened (2006),
òàáë. A4.1, ðèñ. 4.5].
Íà îñíîâå ðàáîòû Ñêîôèëüäà è Ñåíåäà â êà÷åñòâå ñîöèàëüíî-äåìîãðàôè÷åñêèõ ïåðåìåííûõ áûëè èñïîëüçîâàíû obser (ñòåïåíü ñîáëþäåíèÿ ðåëèãèîçíûõ òðàäèöèé — îò 1 äî 4), ashk
(ÿâëÿåòñÿ ëè ðåñïîíäåíò àøêåíàçè — 0 èëè 1), educ (êîëè÷åñòâî ëåò îáðàçîâàíèÿ — îò 0
äî 25), income (äîõîä — îò 1 äî 5) è age (âîçðàñò).
1
http://www.gesis.org/en/services/data/survey-data/eurobarometer
61
R Îáùåñòâî
À. Â. Çàõàðîâ, Äåàí Ôàíòàööèíè
¹2(14) 2009
ÏÐÈÊËÀÄÍÀß ÝÊÎÍÎÌÅÒÐÈÊÀ
¹2(14) 2009
2. Ìîäåëü
Ìû îöåíèâàåì ìîäåëü ìíîæåñòâåííîãî âûáîðà, â êîòîðîé ïîëåçíîñòü èçáèðàòåëÿ i, ïðèïèñûâàåìàÿ ïàðòèè j, ðàâíà:
u ij = a j + g Tj x i -| y j - v i | B i + e ij ,
(2)
| z | B i = z T B i z.
(3)
Ýêîíîìè÷åñêèå ôàêòîðû â ìîäåëè ãîëîñîâàíèÿ: ïðèìåð Íèäåðëàíäîâ, Âåëèêîáðèòàíèè è Èçðàèëÿ
Ïîëîæèòåëüíî îïðåäåëåííàÿ ìàòðèöà B i , çàäàþùàÿ ïðîñòðàíñòâåííóþ ìåòðèêó â ìîäåëè
ãîëîñîâàíèÿ, èìååò âèä:
æ b 1i b 3 i ö÷
,
(4)
B i = çç
è b 3 i b 2 i ÷ø
ãäå b hi = b h1 + b hT 2 x i .
(5)
Äëÿ h = 1, 2, 3 b h1 — ñêàëÿð, b h 2 Î Â L — âåêòîð-ñòîëáåö. Òàêàÿ ìîäåëü ó÷èòûâàåò âëèÿíèå
âåëè÷èí x i íà ìåòðèêó, ñ ïîìîùüþ êîòîðîé èçáèðàòåëü i îöåíèâàåò ïîëèòè÷åñêóþ ïðîãðàììó
êàæäîé èç ïàðòèé.
Ñëó÷àéíûå îøèáêè ïðåäïîëàãàþòñÿ íåçàâèñèìî ðàñïðåäåëåííûìè ñîãëàñíî çàêîíó
P( e ij £ a ) = exp(- exp(-a )).
(6)
Ïðåäïîëàãàåòñÿ, ÷òî èçáèðàòåëü i ïîääåðæèâàåò ïàðòèþ j, åñëè ýòà ïàðòèÿ ïðåäîñòàâëÿåò
èçáèðàòåëþ íàèáîëüøóþ ïîëåçíîñòü. Îáîçíà÷èì z i èíäåêñ ïàðòèè, çà êîòîðóþ ñîáèðàåòñÿ
ïðîãîëîñîâàòü èçáèðàòåëü i:
z i = argmax k Î{1K
, , M } u ik .
(7)
Âåðîÿòíîñòü òîãî, ÷òî èçáèðàòåëü i ïðîãîëîñóåò çà ïàðòèþ j, ðàâíà:
Pij = P( j = z i ) =
exp( a j + g j x i -| y j - v i | B i )
M
.
(8)
å exp( a k + g k x i -| y k - v i | B i )
k =1
Ôóíêöèÿ ïðàâäîïîäîáèÿ ìîäåëè åñòü ïðîèçâåäåíèå (8) ïî âñåì èçáèðàòåëÿì:
N
L = Õ Piz i .
(9)
i=1
Îöåíèâàåì ìîäåëü, ìàêñèìèçèðóÿ (9) ïî âåëè÷èíàì a j , g j è ïî ïàðàìåòðàì ìàòðèöû B i .
3. Îöåíêà ìîäåëè
Ìû îöåíèëè íåñêîëüêî ìîäåëåé ñ ðàçëè÷íûìè îãðàíè÷åíèÿìè íà ìåòðèêó B i .
I. Ïðîñòðàíñòâåííàÿ ìîäåëü ãîëîñîâàíèÿ ñî ñòàíäàðòíîé åâêëèäîâîé ìåòðèêîé
æ b 0 ö÷
.
B i = çç
è0 b ÷ø
(10)
Òå æå ìîäåëè áûëè îöåíåíû è â ðàáîòàõ [Quinn, Martin and Whitford [1999]) è (Schofield and
Sened [2006]).
62
Îáùåñòâî R
ÏÐÈÊËÀÄÍÀß ÝÊÎÍÎÌÅÒÐÈÊÀ
II. Ïðîñòðàíñòâåííàÿ ìîäåëü ãîëîñîâàíèÿ, â êîòîðîé ïåðâîå è âòîðîå èçìåðåíèÿ ïîëèòè÷åñêîãî ïðîñòðàíñòâà èìåþò ðàçíóþ âàæíîñòü. Òåì íå ìåíåå âàæíîñòü ïåðâîãî è âòîðîãî èçìåðåíèé îäèíàêîâà äëÿ âñåõ èçáèðàòåëåé. Ïðîñòðàíñòâåííàÿ ìåòðèêà èìååò âèä:
æb 1
B i = çç
è0
0 ö÷
.
b 2 ÷ø
(11)
III. Ïðîñòðàíñòâåííàÿ ìîäåëü ãîëîñîâàíèÿ c ïåðåêðåñòíûì ýôôåêòîì, â êîòîðîé âàæíîñòü îáîèõ èçìåðåíèé îäèíàêîâà äëÿ âñåõ èçáèðàòåëåé:
æ b1
B i = çç
èb 3
b 3 ö÷
.
b 2 ÷ø
(12)
IV. Ìîäåëü, â êîòîðîé âàæíîñòü ïåðâîãî è âòîðîãî èçìåðåíèé îäèíàêîâà äëÿ êàæäîãî èçáèðàòåëÿ, îäíàêî çàâèñèò îò åãî ñîöèàëüíî-äåìîãðàôè÷åñêèõ õàðàêòåðèñòèê. Ñîîòâåòñòâóþùàÿ ïðîñòðàíñòâåííàÿ ìåòðèêà çàäàåòñÿ êàê
æ b i 0 ö÷
,
(13)
B i = çç
è 0 b i ÷ø
ãäå b i = b1 + b 2T x i .
(14)
Ïðè ñïåöèôèêàöèè (13)—(14) âîçìîæíî, ÷òî äëÿ íåêîòîðûõ ðåñïîíäåíòîâ îöåíåííàÿ ìàòðèöà (13) áóäåò îòðèöàòåëüíî îïðåäåëåíà, âñëåäñòâèå ÷åãî îöåíåííàÿ ôóíêöèÿ ïîëåçíîñòè
íå áóäåò èìåòü ñìûñëà. Îäíà èç âîçìîæíûõ àëüòåðíàòèâ — îïðåäåëèòü ìîäåëü òàê, ÷òîáû êîýôôèöèåíòû b i âñåãäà áûëè ïîëîæèòåëüíû, íàïðèìåð, ïîñòàâèòü b i = exp(b1 + b 2T x i ). Ê ñîæàëåíèþ, ïðè òàêîé ñïåöèôèêàöèè ìîäåëè ôóíêöèÿ ïðàâäîïîäîáèÿ (9) ïåðåñòàåò áûòü âîãíóòîé, ÷òî âûçûâàåò òðóäíîñòè ñ åå ìàêñèìèçàöèåé (àâòîðû íå ñìîãëè ýòîãî ñäåëàòü, èñïîëüçóÿ
ïðîãðàììíûå ïàêåòû Stata 8.0 è Gauss). Ê ñ÷àñòüþ, äëÿ êàæäîãî èç òðåõ íàáîðîâ äàííûõ âñå
êîýôôèöèåíòû b i áûëè ïîëîæèòåëüíû.
V. Ìîäåëü, â êîòîðîé âàæíîñòü ïåðâîãî è âòîðîãî èçìåðåíèé ðàçíàÿ äëÿ êàæäîãî èçáèðàòåëÿ è çàâèñèò îò åãî ñîöèàëüíî-äåìîãðàôè÷åñêèõ õàðàêòåðèñòèê.
Ïðîñòðàíñòâåííàÿ ìåòðèêà çàäàåòñÿ êàê
æb 1
B i = çç i
è0
0
b 1i
÷ö ,
÷ø
(15)
T
T
ãäå b 1i = b11 + b12
x i , b 2 i = b 21 + b 22
xi .
(16)
VI. Ìîäåëü c ïåðåêðåñòíûì ýôôåêòîì, â êîòîðîé âàæíîñòü ïåðâîãî è âòîðîãî èçìåðåíèé ðàçíàÿ äëÿ êàæäîãî èçáèðàòåëÿ è çàâèñèò îò åãî ñîöèàëüíî-äåìîãðàôè÷åñêèõ õàðàêòåðèñòèê:
æ b1
B i = çç i
èb 3i
b 3i
b 2i
÷ö ,
÷ø
(17)
T
T
T
ãäå b 1i = b11 + b12
x i , b 2 i = b 21 + b 22
x i , b 3 i = b 31 + b 32
xi .
(18)
Äëÿ Íèäåðëàíäîâ ìû ðàññìàòðèâàëè âûáîð ìåæäó 4 ïàðòèÿìè: Ïàðòèÿ òðóäà (PvDA), Áëîê
õðèñòèàíñêèõ äåìîêðàòîâ (CDA), ëèáåðàëüíàÿ Íàðîäíàÿ ïàðòèÿ çà ñâîáîäó è äåìîêðàòèþ
63
R Îáùåñòâî
À. Â. Çàõàðîâ, Äåàí Ôàíòàööèíè
¹2(14) 2009
ÏÐÈÊËÀÄÍÀß ÝÊÎÍÎÌÅÒÐÈÊÀ
¹2(14) 2009
Ýêîíîìè÷åñêèå ôàêòîðû â ìîäåëè ãîëîñîâàíèÿ: ïðèìåð Íèäåðëàíäîâ, Âåëèêîáðèòàíèè è Èçðàèëÿ
(VVD), ðàäèêàëüíàÿ Äåìîêðàòè÷åñêàÿ ïàðòèÿ D66. Äëÿ Âåëèêîáðèòàíèè áûëè ðàññìîòðåíû
ìîäåëè âûáîðà ìåæäó 3 îñíîâíûìè ïàðòèÿìè: ëèáåðàëîâ (Labor), êîíñåðâàòîðîâ (Conservative) è ëèáåðàëüíûõ äåìîêðàòîâ (Liberal). Äëÿ Èçðàèëÿ áûëà ðàññìîòðåíà ìîäåëü âûáîðà ìåæäó 7 ïàðòèÿìè: Ïàðòèÿ òðóäà (Labor), íàöèîíàëèñòè÷åñêàÿ ïàðòèÿ Likud, ñîöèàë-äåìîêðàòè÷åñêàÿ ïàðòèÿ Meretz, ïàðòèÿ Third Way, òðè ðåëèãèîçíûå ïàðòèè — Mafdal, Modelet
è Shas.
Ïî âîçìîæíîñòè ìû ñðàâíèâàëè ìîäåëè ïðè ïîìîùè òåñòà îòíîøåíèÿ ïðàâäîïîäîáèÿ,
ðåçóëüòàòû ýòèõ òåñòîâ ïðèâåäåíû â òàáë. 1, 2.  êàæäîé êëåòêå òàáëèöû ïåðâîå çíà÷åíèå åñòü
ðàçíèöà ìåæäó ëîãàðèôìàìè ïðàâäîïîäîáèÿ äâóõ ñðàâíèâàåìûõ ìîäåëåé; âòîðîå çíà÷åíèå — ðàçíèöà â ÷èñëå ñòåïåíåé ñâîáîäû äâóõ ìîäåëåé, òðåòüå çíà÷åíèå — p-ñòàòèñòèêà
òåñòà îòíîøåíèÿ ïðàâäîïîäîáèÿ.  çàãîëîâêàõ ñòîëáöîâ è ñòðîê òàáëèöû îáîçíà÷åíû ïàðàìåòðû, âõîäÿùèå â ìàòðèöó B i äëÿ êàæäîé ìîäåëè. Íàïðèìåð, 1-é ñòîëáåö òàáë. 1 ñîîòâåòñòâóåò ìîäåëè I; 6-é ñòîëáåö — ìîäåëè V, â êîòîðîé â êîýôôèöèåíò b 1 â êà÷åñòâå ðåãðåññîðà âõîäèò educ, à â êîýôôèöèåíò b 2 — manlab.
Òàáëèöà 1
Òåñò îòíîøåíèÿ ïðàâäîïîäîáèÿ äëÿ Íèäåðëàíäîâ
Ìîäåëü I
Ìîäåëü II
b 1: const
b 1: const
b 2: const
Ìîäåëü II
b 1: const
0,44
b 2: const
1
Ìîäåëü III Ìîäåëü IV Ìîäåëü IV Ìîäåëü V
b 1: const
b 2: const
b 3: const
b 1: const,
educ
b 1: âñå
b 1: const,
educ
b 2: const,
manlab
Ìîäåëü V
b 1: âñå
b 2: âñå
—
0,34
Ìîäåëü III
b 1: const
0,55
0,11
b 2: const
2
1
b 3: const
0,57
Ìîäåëü IV
b 1: const, educ
4,46
—
0,639
1
—
0,003
Ìîäåëü IV
b 1: âñå
5,51
1,05
5
4
0,051
Ìîäåëü V
b 1: const, educ
12,3
—
0,71
11,86
7,84
64
Îáùåñòâî R
ÏÐÈÊËÀÄÍÀß ÝÊÎÍÎÌÅÒÐÈÊÀ
Îêîí÷àíèå òàáë. 1
b 2: const, manlab
Ìîäåëü I
Ìîäåëü II
b 1: const
b 1: const
b 2: const
Ìîäåëü III Ìîäåëü IV Ìîäåëü IV Ìîäåëü V
b 1: const
b 2: const
b 3: const
b 1: const,
educ
b 1: âñå
b 1: const,
educ
b 2: const,
manlab
3
2
2
0,00002
0,00001
0,0003
Ìîäåëü V
b 1: âñå
14,68
14,22
10,22
9,1700
2,34
b 2: âñå
11
10
10
6
8
0,029
0,0062
0,79
7,22
0,002
0,0015
Ìîäåëü VI
b 1: âñå
19,53
19,09
18,98
15,07
14,0200
b 2: âñå
17
16
15
16
12
b 3: âñå
0,0018
0,0015
0,0009
0,013
Ìîäåëü V
b 1: âñå
b 2: âñå
4,85
14
0,0055
6
0,44
0,13
Òàáëèöà 2
Òåñò îòíîøåíèÿ ïðàâäîïîäîáèÿ äëÿ Âåëèêîáðèòàíèè
Ìîäåëü I
Ìîäåëü II
b 1: const
b 1: const
b 2: const
Ìîäåëü II
b 1: const
0,27
b 2: const
1
Ìîäåëü III Ìîäåëü IV Ìîäåëü IV Ìîäåëü V
b 1: const
b 2: const
b 3: const
b 1: const,
educ
b 1: âñå
b 1: const,
educ
b 2: const,
manlab
Ìîäåëü V
b 1: âñå
b 2: âñå
—
0,47
Ìîäåëü III
b 1: const
0,28
0,01
b 2: const
2
1
b 3: const
0,77
0,92
Ìîäåëü IV
b 1: const, educ
—
2,110
1
—
0,004
65
R Îáùåñòâî
À. Â. Çàõàðîâ, Äåàí Ôàíòàööèíè
¹2(14) 2009
ÏÐÈÊËÀÄÍÀß ÝÊÎÍÎÌÅÒÐÈÊÀ
¹2(14) 2009
Îêîí÷àíèå òàáë. 2
Ìîäåëü I
Ìîäåëü II
b 1: const
b 1: const
b 2: const
Ýêîíîìè÷åñêèå ôàêòîðû â ìîäåëè ãîëîñîâàíèÿ: ïðèìåð Íèäåðëàíäîâ, Âåëèêîáðèòàíèè è Èçðàèëÿ
Ìîäåëü IV
b 1: âñå
Ìîäåëü III Ìîäåëü IV Ìîäåëü IV Ìîäåëü V
b 1: const
b 2: const
b 3: const
b 1: const,
educ
2,93
0,82
5
4,00
Ìîäåëü V
b 1: const, educ
5,8700
5,6,000
3,7700
b 2: const, manlab
4
3
3
0,0194
0,0107
0,0576
7,9600
7,7000
5,850
Ìîäåëü V
b 1: âñå
b 2: âñå
11
10
0,1181
Ìîäåëü VI
b 1: âñå
12,0800
11,8100
18,9800
b 2: âñå
17
16
15
b 3: âñå
0,1152
0,0981
0,0009
b 1: const,
educ
b 2: const,
manlab
2,0900
6
7
0,305
0,1213
0,7588
9,970
9,1500
6,2100
16
0,229
b 1: âñå
b 2: âñå
—
5,0400
10
0,1441
b 1: âñå
Ìîäåëü V
12
0,1069
13
0,4935
4,120
6
0,221
Äëÿ âñåõ èññëåäóåìûõ ñòðàí (Íèäåðëàíäû, Âåëèêîáðèòàíèÿ è Èçðàèëü) ìîäåëè II è III ñ ïîñòîÿííûìè êîýôôèöèåíòàìè íå ïðèíîñÿò óëó÷øåíèÿ íàä ìîäåëüþ I. Ëîãàðèôìû êîýôôèöèåíòîâ
ïðàâäîïîäîáèÿ äëÿ âñåõ òðåõ ìîäåëåé ïðèìåðíî îäèíàêîâû (ñì. òàáë. 1, 2). Îòìåòèì, ÷òî äëÿ Íèäåðëàíäîâ êîýôôèöèåíòû b 1 è b 2 ÿâëÿþòñÿ çíà÷èìûìè êàê â ìîäåëè II, òàê è â ìîäåëè III, à êîýôôèöèåíò b 3 â ìîäåëè III íåçíà÷èì.  òî æå âðåìÿ â Âåëèêîáðèòàíèè â ìîäåëÿõ II, III çíà÷èì òîëüêî
êîýôôèöèåíò b 1 . Ýòî îçíà÷àåò, ÷òî ïîëèòèêà â Âåëèêîáðèòàíèè áîëåå îäíîìåðíà — íà ýëåêòîðàëüíîå ïîâåäåíèå èçáèðàòåëÿ âëèÿåò òîëüêî çíà÷åíèå ïåðâîãî ôàêòîðà ïîëèòè÷åñêèõ ïðåäïî÷òåíèé. Äëÿ Èçðàèëÿ æå âñå òðè êîýôôèöèåíòà â ìîäåëè III ÿâëÿþòñÿ çíà÷èìûìè. Äëÿ âñåõ òðåõ
ñòðàí ìàòðèöû B i â ìîäåëè III ÿâëÿþòñÿ ïîëîæèòåëüíî îïðåäåëåííûìè.
Îöåíêà âåðîÿòíîñòè òîãî, ÷òî äàííûé èçáèðàòåëü ïðîãîëîñóåò çà êàæäóþ èç 4 ïîëèòè÷åñêèõ ïàðòèé, ïðèâåäåíà â òàáë. 3. Ìû ðàññìàòðèâàåì ìîäåëü IV äëÿ Íèäåðëàíäîâ. Êàæäàÿ
ñòðîêà òàáëèöû ñîîòâåòñòâóåò ãèïîòåòè÷åñêîìó èçáèðàòåëþ ñ çàäàííûìè íàìè ñîöèàëüíîýêîíîìè÷åñêèìè õàðàêòåðèñòèêàìè è ïîëèòè÷åñêèìè ïðåäïî÷òåíèÿìè (v1 è v2). Âñå ïåðåìåííûå, êðîìå educ, çàôèêñèðîâàíû íà ñðåäíåâçâåøåííîì óðîâíå. Çíà÷åíèÿ 0,81 è 0,53 ñîîòâåòñòâóþò îäíîìó ñòàíäàðòíîìó îòêëîíåíèþ 1-ãî è 2-ãî ïðîñòðàíñòâåííûõ ôàêòîðîâ ïîëèòè÷åñêèõ
ïðåäïî÷òåíèé èçáèðàòåëÿ. Ìîæíî âèäåòü, ÷òî ó èçáèðàòåëåé ñ áîëåå âûñîêèì îáðàçîâàíèåì
(educ = 9) îöåíåííûå âåðîÿòíîñòè ãîëîñîâàíèÿ ãîðàçäî ñèëüíåå çàâèñÿò îò ïîëèòè÷åñêèõ
ïðåäïî÷òåíèé, ÷åì ó èçáèðàòåëåé ñ íèçêèì óðîâíåì îáðàçîâàíèÿ (educ = 1).
66
Îáùåñòâî R
ÏÐÈÊËÀÄÍÀß ÝÊÎÍÎÌÅÒÐÈÊÀ
Òàáëèöà 3
Îöåíêè âåðîÿòíîñòè èçáèðàòåëÿ ïðîãîëîñîâàòü
çà êàæäóþ èç 4 ïàðòèé äëÿ Íèäåðëàíäîâ (ìîäåëü IV)
educ = 1
educ = 9
v1
v2
PvDA
VVD
CDA
D66
0,00
0,00
0,49
0,13
0,29
0,09
0,00
0,53
0,45
0,14
0,34
0,07
0,00
–0,53
0,52
0,12
0,27
0,09
0,81
0,00
0,23
0,27
0,43
0,07
–0,81
0,00
0,73
0,05
0,16
0,06
0,00
0,00
0,16
0,16
0,39
0,29
0,00
0,53
0,13
0,17
0,53
0,17
0,00
–0,53
0,19
0,13
0,24
0,44
0,81
0,00
0,01
0,56
0,37
0,06
–0,81
0,00
0,74
0,02
0,05
0,19
 ìîäåëè IV äëÿ Íèäåðëàíäîâ òîëüêî êîýôôèöèåíò ïðè educ èç âåêòîðà b 2 áûë ñòàòèñòè÷åñêè çíà÷èìûì, îñòàëüíûå 4 êîýôôèöèåíòà — ïðè stown, income, manlab è relig — íåçíà÷èìû
êàê ïî îòäåëüíîñòè, òàê è ñîâìåñòíî (èõ èñêëþ÷åíèå ñíèæàåò ëîãàðèôì ïðàâäîïîäîáèÿ âñåãî íà 1,05).
 òàáë. 4 ïðèâåäåíû ðåçóëüòàòû îöåíîê ìîäåëè IV äëÿ Âåëèêîáðèòàíèè. Äëÿ ýòîé ñòðàíû
îáðàçîâàíèå èìååò àíàëîãè÷íûé, íî çíà÷èòåëüíî áîëåå ñëàáûé ýôôåêò íà b 2 . Ïðè ýòîì ñîîòâåòñòâóþùèé êîýôôèöèåíò çíà÷èì òîëüêî íà óðîâíå 5%. Îñòàëüíûå 4 êîýôôèöèåíòà, êàê äëÿ
Íèäåðëàíäîâ, ÿâëÿþòñÿ íåçíà÷èìûìè.
Äëÿ Èçðàèëÿ â ìîäåëè IV åäèíñòâåííûé çíà÷èìûé êîýôôèöèåíò â b 2 (êðîìå êîíñòàíòû)
áûë ïðè relig. Ïðè ïðî÷èõ ðàâíûõ, ÷åëîâåê, íå ñîáëþäàþùèé ðåëèãèîçíûå îãðàíè÷åíèÿ, áóäåò áîëåå îñòðî ðåàãèðîâàòü íà èçìåíåíèÿ â ïîëèòè÷åñêèõ ïðîãðàììàõ ïàðòèé.
Òàáëèöà 4
Ðåçóëüòàòû îöåíêè ìîäåëè IV äëÿ Âåëèêîáðèòàíèè
Ïàðàìåòðû
Labor
Êîýôôèöèåíò
Ñòàíäàðòíàÿ îøèáêà
const
0,432
0,497
manlab
1,060
0,269
relig
–0,214
0,111
income
–0,107
0,054
stown
0,056
0,162
educ
0,063
0,055
67
R Îáùåñòâî
À. Â. Çàõàðîâ, Äåàí Ôàíòàööèíè
¹2(14) 2009
ÏÐÈÊËÀÄÍÀß ÝÊÎÍÎÌÅÒÐÈÊÀ
¹2(14) 2009
Îêîí÷àíèå òàáë. 4
Ïàðàìåòðû
Liberal Democrats
Ñòàíäàðòíàÿ îøèáêà
–0,980
0,250
manlab
0,412
0,397
relig
0,022
0,151
income
–0,105
0,071
stown
–0,247
0,221
educ
0,117
0,065
const
0,460
0,194
manlab
–0,011
0,102
relig
–0,009
0,042
income
–0,024
0,021
stown
–0,025
0,065
educ
0,045
0,023
const
b
Ýêîíîìè÷åñêèå ôàêòîðû â ìîäåëè ãîëîñîâàíèÿ: ïðèìåð Íèäåðëàíäîâ, Âåëèêîáðèòàíèè è Èçðàèëÿ
Êîýôôèöèåíò
Ëîãàðèôì êîýôôèöèåíòà ïðàâäîïîäîáèÿ
–358,706
B íå ÿâëÿåòñÿ ïîëîæèòåëüíî îïðåäåëåííîé
0%
Ïðèìå÷àíèå. Ïåðâûå äâå ãðóïïû îöåíåííûõ ïàðàìåòðîâ ñîîòâåòñòâóþò ïàðàìåòðàì y j è a j (const) äëÿ
äâóõ èç òðåõ ïîëèòè÷åñêèõ ïàðòèé. Äëÿ òðåòüåé ïàðòèè (êîíñåðâàòîðîâ) ýòè ïàðàìåòðû ïðèðàâíåíû ê 0, òàê
êàê ýòî íåîáõîäèìî äëÿ èäåíòèôèêàöèè ìîäåëè. Ïîñëåäíÿÿ ãðóïïà ïàðàìåòðîâ ñîîòâåòñòâóåò b2 è b1 (const).
Ñëåäóþùàÿ ñòðîêà — ëîãàðèôì êîýôôèöèåíòà ïðàâäîïîäîáèÿ (9). Íàêîíåö, ìû ñ÷èòàåì, êàêîé ïðîöåíò
èç îöåíåííûõ ìàòðèö B i ÿâëÿåòñÿ ïîëîæèòåëüíî îïðåäåëåííûì.
 ìîäåëè V äëÿ Íèäåðëàíäîâ áûëè çíà÷èìû êîýôôèöèåíòû ïðè educ â âåêòîðå b12 , à òàêæå
êîýôôèöèåíò ïðè manlab â âåêòîðå b 22 (òàáë. 5).
Äëÿ Âåëèêîáðèòàíèè â ìîäåëè V òîëüêî êîýôôèöèåíò ïðè stown èç âåêòîðà b 22 áûë èíäèâèäóàëüíî çíà÷èì. Ìîäåëü ñ îãðàíè÷åíèÿìè, â êîòîðîé áûëè ñîõðàíåíû êîýôôèöèåíò educ
èç âåêòîðà b12 è êîýôôèöèåíòû manlab è stown èç âåêòîðà b 22 , ïîêàçàëà ëó÷øèé ðåçóëüòàò
â ïëàíå òåñòà îòíîøåíèÿ ïðàâäîïîäîáèÿ.
Òàáëèöà 5
Ðåçóëüòàòû îöåíêè ìîäåëè V äëÿ Íèäåðëàíäîâ
Ïàðàìåòð
PvDA
Êîýôôèöèåíò
Ñòàíäàðòíàÿ îøèáêà
const
1,836
0,617
manlab
1,469
0,633
relig
0,078
0,165
income
–0,044
0,045
68
Îáùåñòâî R
ÏÐÈÊËÀÄÍÀß ÝÊÎÍÎÌÅÒÐÈÊÀ
Îêîí÷àíèå òàáë. 5
Ïàðàìåòð
VVD
CDA
b1
b2
Êîýôôèöèåíò
Ñòàíäàðòíàÿ îøèáêà
stown
0,353
0,249
educ
–0,188
0,062
const
–0,146
0,758
manlab
–0,372
0,854
relig
0,054
0,185
income
0,120
0,051
stown
0,238
0,287
educ
0,015
0,070
const
–1,603
0,756
manlab
1,178
0,679
relig
1,423
0,193
income
0,035
0,050
stown
0,537
0,272
educ
–0,098
0,066
const
0,263
0,096
educ
0,116
0,027
const
1,084
0,280
manlab
–1,217
0,746
Ëîãàðèôì ïðàâäîïîäîáèÿ
–422,621
B íå ÿâëÿåòñÿ ïîëîæèòåëüíî îïðåäåëåííîé
14,74%
Ïðèìå÷àíèå. Èç b1, b 2 ñîõðàíåíû òîëüêî çíà÷èìûå êîýôôèöèåíòû.
Äëÿ Èçðàèëÿ ìîäåëü VI íå ïðèâåëà ê óëó÷øåíèþ íàä ìîäåëÿìè I è III (òàáë. 6).
Òàáëèöà 6
Ðåçóëüòàòû îöåíêè ìîäåëè VI äëÿ Èçðàèëÿ
Ïàðàìåòð
Likud
Êîýôôèöèåíò
Ñòàíäàðòíàÿ îøèáêà
const
10,729
2,789
educ
–0,044
0,075
age
0,007
0,015
ashk
–0,556
0,915
income
–0,153
0,379
obser
–0,454
0,673
69
R Îáùåñòâî
À. Â. Çàõàðîâ, Äåàí Ôàíòàööèíè
¹2(14) 2009
ÏÐÈÊËÀÄÍÀß ÝÊÎÍÎÌÅÒÐÈÊÀ
¹2(14) 2009
Ïðîäîëæåíèå òàáë. 6
Ïàðàìåòð
Avoda
Ýêîíîìè÷åñêèå ôàêòîðû â ìîäåëè ãîëîñîâàíèÿ: ïðèìåð Íèäåðëàíäîâ, Âåëèêîáðèòàíèè è Èçðàèëÿ
Modelet
Mafdal
Third
Shas
Êîýôôèöèåíò
Ñòàíäàðòíàÿ îøèáêà
const
6,547
2,560
educ
0,029
0,065
age
0,026
0,013
ashk
–0,287
0,831
income
–0,116
0,333
obser
–0,002
0,645
const
3,343
2,502
educ
0,285
0,098
age
0,037
0,019
ashk
0,259
0,756
income
–0,078
0,301
obser
–2,240
0,554
const
1,031
2,893
educ
0,107
0,130
age
0,005
0,024
ashk
0,651
0,915
income
–0,156
0,311
obser
–1,064
0,638
Way
const
4,363
educ
0,015
0,111
age
0,013
0,021
ashk
0,370
1,126
income
–0,210
0,469
obser
0,153
0,808
const
10,863
3,643
educ
–0,244
0,128
age
–0,035
0,026
ashk
0,056
1,304
income
0,317
0,456
70
Îáùåñòâî R
ÏÐÈÊËÀÄÍÀß ÝÊÎÍÎÌÅÒÐÈÊÀ
Îêîí÷àíèå òàáë. 6
Ïàðàìåòð
b1
b2
b3
Êîýôôèöèåíò
Ñòàíäàðòíàÿ îøèáêà
obser
–1,714
0,859
const
2,936
0,613
ashk
–0,523
0,324
income
–0,138
0,099
const
2,279
0,752
ashk
–0,387
0,496
obser
–0,599
0,216
const
–3,833
1,062
ashk
0,865
0,659
obser
0,872
0,278
Ëîãàðèôì ïðàâäîïîäîáèÿ
–644,990
B íå ÿâëÿåòñÿ ïîëîæèòåëüíî îïðåäåëåííîé
46,65%
Ïðèìå÷àíèå. Èç b1, b 2, b 3 ñîõðàíåíû òîëüêî çíà÷èìûå êîýôôèöèåíòû.
Äëÿ Íèäåðëàíäîâ è Âåëèêîáðèòàíèè ìîäåëü VI íå ïîêàçûâàåò ëó÷øèé ðåçóëüòàò, ÷åì ìîäåëü V, ò. å. b 31 è âñå êîýôôèöèåíòû èç b 32 ÿâëÿþòñÿ ñîâìåñòíî íåçíà÷èìûìè. Äëÿ Èçðàèëÿ ñîîòâåòñòâóþùèå êîýôôèöèåíòû áûëè çíà÷èìûìè íà óðîâíå 5% (ñì. òàáë. 6). Çíà÷åíèå ëîãàðèôìà ïðàâäîïîäîáèÿ äëÿ ìîäåëè ñ îãðàíè÷åíèÿìè, â êîòîðîé ñîõðàíåíû ashk è income â b12 ,
à òàêæå ashk è obser â b 22 è b 32 , âñåãî íà 2,92 íèæå, ÷åì äëÿ ìîäåëè áåç îãðàíè÷åíèé.
Çàêëþ÷åíèå
 ñòàíäàðòíîé ôîðìóëèðîâêå âåðîÿòíîñòíîé ìîäåëè ãîëîñîâàíèÿ îöåíêà èçáèðàòåëåì
ïîëèòè÷åñêîé ïàðòèè çàâèñèò êàê îò ïðîãðàììû ïàðòèè, òàê è îò ñîöèàëüíî-äåìîãðàôè÷åñêèõ õàðàêòåðèñòèê èçáèðàòåëÿ.  äàííîé ñòàòüå ïðåäïîëàãàåòñÿ, ÷òî ïðåäïî÷òåíèÿ èçáèðàòåëåé îïèñûâàþòñÿ áîëåå îáùåé, ÷åì â óêàçàííûõ ðàáîòàõ, ôóíêöèåé ïîëåçíîñòè.  ÷àñòíîñòè, ïîëåçíîñòü, ïðèïèñûâàåìàÿ èçáèðàòåëåì ïîëèòè÷åñêîé ïàðòèè, ÿâëÿåòñÿ ôóíêöèåé
îò îáîáùåííîãî åâêëèäîâà ðàññòîÿíèÿ ìåæäó ïîëèòè÷åñêîé ïðîãðàììîé ïàðòèè è íàèëó÷øåé àëüòåðíàòèâîé èçáèðàòåëÿ. Ïîêàçàíî, ÷òî äëÿ Íèäåðëàíäîâ (è â ìåíüøåé ìåðå äëÿ Âåëèêîáðèòàíèè) ïàðàìåòðû ýòîé ìåòðèêè çàâèñÿò îò èíäèâèäóàëüíûõ õàðàêòåðèñòèê èçáèðàòåëÿ,
â ïåðâóþ î÷åðåäü — îò åãî îáðàçîâàíèÿ.
Òàêèì îáðàçîì, ñîöèàëüíî-äåìîãðàôè÷åñêèå õàðàêòåðèñòèêè âëèÿþò íà ñòåïåíü çíà÷èìîñòè äëÿ èçáèðàòåëÿ òåõ èëè èíûõ àñïåêòîâ ïîëèòè÷åñêèõ ïðîãðàìì ïàðòèé.  Âåëèêîáðèòàíèè
è Íèäåðëàíäàõ áîëåå îáðàçîâàííûå èçáèðàòåëè óäåëÿþò áîëüøåå âíèìàíèå ïîëèòè÷åñêèì
ïðîãðàììàì ïàðòèé.  Èçðàèëå àíàëîãè÷íóþ ðîëü èãðàåò ñîáëþäåíèå èçáèðàòåëåì åâðåéñêèõ
ðåëèãèîçíûõ òðàäèöèé. Ëþäè, íå ñîáëþäàþùèå òðàäèöèè, áîëåå ñêëîííû ãîëîñîâàòü çà òå ïàðòèè, ÷üÿ ïîçèöèÿ íàèáîëåå ñîîòâåòñòâóåò èõ ïîëèòè÷åñêèì âçãëÿäàì.
71
R Îáùåñòâî
À. Â. Çàõàðîâ, Äåàí Ôàíòàööèíè
¹2(14) 2009
ÏÐÈÊËÀÄÍÀß ÝÊÎÍÎÌÅÒÐÈÊÀ
Ýêîíîìè÷åñêèå ôàêòîðû â ìîäåëè ãîëîñîâàíèÿ: ïðèìåð Íèäåðëàíäîâ, Âåëèêîáðèòàíèè è Èçðàèëÿ
¹2(14) 2009
 òî æå âðåìÿ íå ïîäòâåðäèëàñü ãèïîòåçà î òîì, ÷òî ïðîñòðàíñòâåííàÿ ìåòðèêà ïîëèòè÷åñêèõ ïðåäïî÷òåíèé èçáèðàòåëåé ÿâëÿåòñÿ íåñòàíäàðòíîé åâêëèäîâîé.
Îöåíêà è èíòåðïðåòàöèÿ ðåçóëüòàòîâ ìîäåëåé (15)—(16) è (17)—(18) áûëè çàòðóäíåíû, òàê
êàê äëÿ çíà÷èòåëüíîé ÷àñòè íàáëþäåíèé îöåíåííûå ìàòðèöû B i íå ÿâëÿþòñÿ ïîëîæèòåëüíî
îïðåäåëåííûìè. Ïîïûòêè îïðåäåëèòü ìîäåëü òàêèì îáðàçîì, ÷òîáû óñëîâèå íà ïîëîæèòåëüíóþ îïðåäåëåííîñòü B i âûïîëíÿëîñü âñåãäà, ïðèâîäèëè ê íåâîãíóòîñòè ôóíêöèè ïðàâäîïîäîáèÿ, ÷òî âûçûâàëî òðóäíîñòè ïðè åå ìàêñèìèçàöèè.
Ðåçóëüòàòû äàííîé ñòàòüè ìîæíî ñðàâíèòü ñ ðàáîòîé Àäàìñà è Ýçðîó [Adams and Ezrow
(2008)]. Èññëåäóÿ îïðîñíûå äàííûå 12 çàïàäíîåâðîïåéñêèõ ñòðàí ñ äåìîêðàòè÷åñêèìè òðàäèöèÿìè íà ïðîòÿæåíèè íåñêîëüêèõ ëåò, îíè ïîñòðîèëè èíäåêñ ãðàæäàíñêîé àêòèâíîñòè äëÿ êàæäîãî èç ðåñïîíäåíòîâ. Áûëî ïîêàçàíî, ÷òî áîëåå âûñîêîå çíà÷åíèå èíäåêñà ñâîéñòâåííî èçáèðàòåëåì ñ áîëåå ëåâûìè ïîëèòè÷åñêèìè âçãëÿäàìè. Òàêæå áûëî ïîêàçàíî, ÷òî ïàðòèè ñêëîííû
èçìåíÿòü ñâîè ïîëèòè÷åñêèå ïðîãðàììû â îòâåò íà èçìåíåíèå ïîëèòè÷åñêèõ ïðåäïî÷òåíèé èçáèðàòåëåé ñ âûñîêèìè çíà÷åíèÿìè èíäåêñà ãðàæäàíñêîé àêòèâíîñòè. Ýòà çàâèñèìîñòü êîñâåííî
ïîäòâåðæäàåò îñíîâíîé âûâîä äàííîé ñòàòüè, òàê êàê äëÿ Âåëèêîáðèòàíèè è Íèäåðëàíäîâ áîëåå
îáðàçîâàííûå èçáèðàòåëè èìåþò áîëåå âûñîêèå çíà÷åíèÿ 1-ãî ôàêòîðà ïîëèòè÷åñêèõ ïðåäïî÷òåíèé è áîëåå íèçêèå çíà÷åíèÿ 2-ãî ôàêòîðà, à âûñîêàÿ ãðàæäàíñêàÿ àêòèâíîñòü ñâîéñòâåííà
â ïåðâóþ î÷åðåäü áîëåå îáðàçîâàííûì ñëîÿì íàñåëåíèÿ.
Ñïèñîê ëèòåðàòóðû
Çàõàðîâ À. Â. Îöåíêà ðàçìåæåâàíèÿ ýëåêòîðàëüíîãî ïðîñòðàíñòâà è ïîñòðîåíèå ìàòåìàòè÷åñêîé ìîäåëè âûáîðà èçáèðàòåëÿ // Ïðèêëàäíàÿ ýêîíîìåòðèêà. 2008.
Adams J. Policy divergence in multicandidate probabilistic spatial voting // Public. Choice. 1999. ¹ 100. P. 103–122.
Adams J. Party competition and responsible party government. Ann Arbor, MI: University of Michigan Press, 2001.
Adams J., Ezrow L. Who do European Parties Represent? How Western European Parties Represent the Policy
Preferences of Opinion Leaders // Journal of Politics. 2009. ¹ 71. P. 206–223.
Adams J., Merrill S. Modelling party strategies and policy representation in multiparty elections: Why are
strategies so extreme? // American Journal of Political Science. 1999. ¹ 43. P. 765–781.
Adams J., Dow J., Merrill S. The Political Consequences of Alienation-Based and Indifference-Based Voter
Abstention: Applications to Presidential Elections // Political Behavior. 2006. ¹ 28(1) P. 65–86.
Alvarez M. R., Nagler J. New Approach to Modeling Strategic Voting in Multiparty Elections // British Journal
of Political Science. 2000. ¹ 30(1). P. 57–75.
Alvarez M. R, Nagler J., Bowler S. Issues, economics and the dynamics of multiparty elections: The 1997 British
general election // American Political Science Review. 2000. ¹ 94. P. 131–150.
Arian A., Shamir M. Elections in Israel. Albany: SUNY Press, 1996.
Ashworth S., Bueno de Mesquita E. Valence Competition and Platform Divergence. Unpublished paper, 2007.
Banks J., Duggan J. Probabilistic Voting in the Spatial Model of Elections: The Theory of Office-Motivated
Candidates / David Austan-Smith and John Duggan, eds. // Social Choice and Strategic Decisions. New York:
Springer, 2004.
Torsten I. Political Leadership and Representation in West European Democracies: A Test of Three Models
of Voting // American Journal of Political Science. 1994. ¹ 38(1). P. 45–74.
Hellwig T. Explaining the Salience of Left-Right Ideology in Postindustrialist Democracies: The Role of Structural
Economic Change // European Journal of Political Research. 2008. ¹ 47(6). P. 687–709.
72
Îáùåñòâî R
ÏÐÈÊËÀÄÍÀß ÝÊÎÍÎÌÅÒÐÈÊÀ
Hellwig T. Globalization, Policy Constraints, and Vote Choice //Journal of Politics. 2008. ¹ 70(4). P. 1128–1141.
Hinich M. Equilibrium in spatial voting: The median voter result is an artifact // Journal of Economic Theory.
1977. ¹ 16. P. 208–219.
Lin Tse-Min, Enelow J., Dorussen H. Equilibrium in Multicandidate Probabilistic Spatial Voting // Public Choice.
1999. ¹ 98. P. 59–82.
McKelvey R., Patty J. W. A Theory of Voting in Large Elections // Games and Economic Behavior. 2006. ¹ 57(1).
P. 155–180.
Merrill S., Grofman B. A Unified Theory of Voting: directional and proximity spatial models // Cambridge
University Press, 1999.
Peress M. Securing the Base: Electoral Competition under Variable Turnout. Mimeo. Universito of Rochester,
2005.
Plane D. L., Gershtenson J. Candidate's ideological locations, abstention, and turnout in US midterm Senate
elections // Political Behavior. 2004. ¹ 26. P. 69–93.
Poole K. T., Rosenthal H. U. S. Presidential Elections 168–1980: A Spatial Analysis // American Journal of Political
Science. 1984. ¹ 28(2). P. 282–312.
Quinn K. M., Martin A. D. An integrated computational model of multiparty electoral competition // Statistical
Science. 2002. ¹ 17. P. 405–419.
Quinn K. M., Martin A. D., Whitford A. B. Voter Choice in Multi-Party Democracies: A Test of Competing Theories
and Models // American Journal of Political Science. 1999. ¹ 43(4). P. 1231–1247.
Rabinowitz G., Macdonald S. E. A Directional Theory of Issue Voting // American Political Science Review. 1989.
¹ 83. P. 93–121.
Schofield N. Equilibrium in the Spatial `Valence' Model of Politics // Journal of Theoretical Politics. 2004. ¹ 16(4).
P. 447–481.
Schofield N. A Valence Model of Political Competition in Britain // Electoral Studies. 2005. ¹ 24(3).
P. 347–370.
Schofield N. The Mean Voter Theorem: Necessary and Sufficient Conditions for Convergent Equilibrium //
Review Of Economic Studies. 2007. ¹ 74. P. 965–980.
Schofield N., Cataife G. A model of political competition with activists applied to the elections of 1989 and
1995 in Argentina // Mathematical Social Sciences. 2007. ¹ 53. P. 213–231.
Schofield N., Ozdemir U. Party Positioning. 2008 (Unpublished manuscript).
Schofield N., Sened I. Local Nash Equilibria in Multipaty Politics // Annals of Operations Reseearch. 2002. ¹ 109.
P. 193–210.
Schofield N., Sened I. Modeling the Interactions of Parties, Activists and Voters: Why is the Political Center
so Empty? // European Journal of Political Research. 2005. ¹ 44(3). P. 355–390.
Schofield N., Sened I. Multiparty Democracy: Elections and Legislative Politics. Cambridge University Press.
2006.
Schofield N., Sened I., Nixon D. Nash equilibrium in multiparty competitionwith «stochastic» voters // Annals
of Operations Research. 1998. ¹ 84. P. 3–27.
Schofield N., Martin A. D., Quinn K. M., Whitford A. B. Multiparty Competition in Netherlands and Germany:
A Model Based on Multinomial Probit // Public Choice. 1998. ¹. 97. P. 257–293.
Stokes D. Spatial models of party competition // American Political Science Review. 1963. ¹ 57. P. 368–377.
Thurder P. W., Eymann A. Policy-Specific Alienation and Indifference in the Calculus of Voting: A Simultaneous
Model of Party Choice and Abstention // Public Choice. 2000. ¹ 102. P. 51–77.
Zakharov A. A Model of Candidate Location and Endogenous Valence // Public Choice. 2008. ¹ 138 (3–4).
73
R Îáùåñòâî
À. Â. Çàõàðîâ, Äåàí Ôàíòàööèíè
¹2(14) 2009