Алгоритм декодирования Витерби с

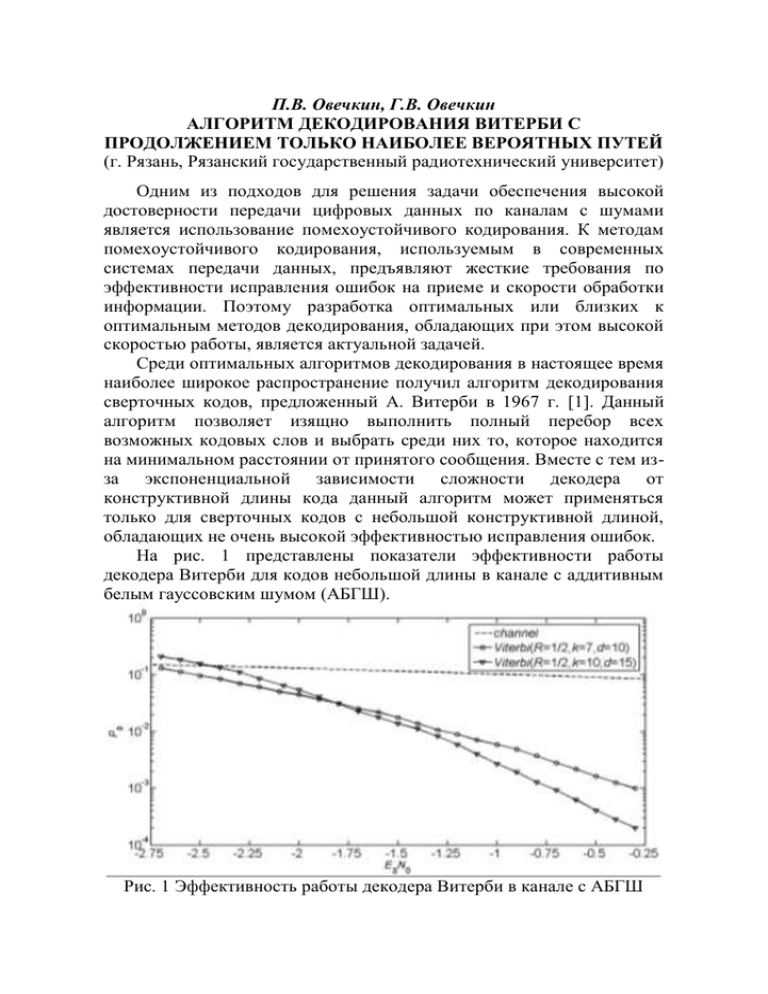
П.В. Овечкин, Г.В. Овечкин
АЛГОРИТМ ДЕКОДИРОВАНИЯ ВИТЕРБИ С
ПРОДОЛЖЕНИЕМ ТОЛЬКО НАИБОЛЕЕ ВЕРОЯТНЫХ ПУТЕЙ
(г. Рязань, Рязанский государственный радиотехнический университет)
Одним из подходов для решения задачи обеспечения высокой
достоверности передачи цифровых данных по каналам с шумами
является использование помехоустойчивого кодирования. К методам
помехоустойчивого кодирования, используемым в современных
системах передачи данных, предъявляют жесткие требования по
эффективности исправления ошибок на приеме и скорости обработки
информации. Поэтому разработка оптимальных или близких к
оптимальным методов декодирования, обладающих при этом высокой
скоростью работы, является актуальной задачей.
Среди оптимальных алгоритмов декодирования в настоящее время
наиболее широкое распространение получил алгоритм декодирования
сверточных кодов, предложенный А. Витерби в 1967 г. [1]. Данный
алгоритм позволяет изящно выполнить полный перебор всех
возможных кодовых слов и выбрать среди них то, которое находится
на минимальном расстоянии от принятого сообщения. Вместе с тем изза экспоненциальной зависимости сложности декодера от
конструктивной длины кода данный алгоритм может применяться
только для сверточных кодов с небольшой конструктивной длиной,
обладающих не очень высокой эффективностью исправления ошибок.
На рис. 1 представлены показатели эффективности работы
декодера Витерби для кодов небольшой длины в канале с аддитивным
белым гауссовским шумом (АБГШ).
Рис. 1 Эффективность работы декодера Витерби в канале с АБГШ
На рисунке по горизонтальной оси отмечено значение отношения
сигнал-шум в канале связи с АБГШ, а по вертикальной – вероятность
ошибки на бит на выходе декодера. При моделировании на вход
декодера Витерби поступали мягкие решения демодулятора (16
уровней квантования), эксперимент продолжался до получения не
менее 1000 ошибок на выходе декодера. Видно, что декодер короткого
кода с R = 1/2, k = 7 и d =10 обладает сравнительно невысокой
эффективностью и снижает вероятность ошибки на два порядка до
уровня 10 -3 при шуме -0.25 дБ в канале. Средняя скорость
декодирования программной версии оптимального декодера Витерби
составила 19000 бит/с на компьютере со средними характеристиками.
Декодер для кодера с большей длиной кодирующего регистра k = 10
обладает большей эффективностью декодирования и снижает
вероятность ошибки на три порядка до уровня 10 -4 при шуме -0.25 дБ
в канале. При этом средняя скорость декодирования данного декодера
существенно падает (до уровня 500 бит/с), так как сложность
оптимального декодирования возрастает экспоненциально с
увеличением длины кода (O(2k)). Отметим, что целью данной работы
не являлось ускорение программных версий за счет оптимизации
программного кода или использования возможностей современных
компьютеров, скорость приведена только для того, чтобы установить
соотношения в скоростях между разными алгоритмическими
подходами к декодированию.
Во многих системах наряду с высокой эффективностью
исправления ошибок предъявляют и жесткие требования к скорости
декодирования информации. Данное требование делает невозможным
использование оптимальных декодеров для длинных (соответственно
и более эффективных) кодов из-за экспоненциально возрастающей от
длины кода сложности декодирования. Для сокращения объема
вычислений при работе декодера можно использовать подход,
который заключается в том, что на каждом шаге декодировании
просматриваются не все возможные пути по кодовой решетке, а только
некоторое подмножество из них. На рис. 2 показаны характеристики
декодера Витерби, для которого на каждом шаге декодирования
отбирались только npath путей с наименьшей метрикой.
Декодер с полным просмотром путей на каждом шаге анализирует
512 состояний декодера, скорость декодирования составляет 500 бит/с.
Декодер с частичным просмотром путей npath = 256 имеет
сопоставимую
эффективность
декодирования,
но
процесс
декодирования выполняется со скоростью 1500 бит/c. Дальнейшее
снижение числа просматриваемых путей npath = 128 повышает
скорость декодирования до 4500 бит/c, но в 2.5 раза повышает и
вероятность ошибки по сравнению с декодером Витерби с полным
перебором.
Рис. 2 Эффективность работы декодера Витерби с неполным
перебором путей в канале с АБГШ
Для данного кода после декодирования с неполным перебором
ветвей существует теоретическая возможность дальнейшего
исправления ошибок до уровня оптимального декодера. Например,
можно использовать декодер другого типа, на вход которого поступает
полученное после декодирования кодовое слово и первоначально
принятое из канала сообщение. Для того чтобы скорость
декодирования
существенно
не
уменьшилась,
необходимо
использовать декодер с линейной сложностью декодирования.
Наиболее подходящим в этом случае может быть использование
двоичного многопорогового декодера (МПД) [2, 3], отличительной
особенностью которого является высокая скорость декодирования
наряду с хорошей эффективностью. Так как после декодирования
Витерби с неполным перебором (npath = 256) в области его
эффективной работы остается не более 0.1% ошибок, то
предполагается, что при поступлении в информационный регистр
несистематического МПД декодированной последовательности с
формированием синдрома на базе принятого из канала сообщения
уровень ошибок будет уменьшен до уровня алгоритма с полным
перебором.
Так как сложность многопорогового декодера возрастает линейно
с увеличением длины кода, то сложность декодирования такой схемы
будет в существенной степени определяться скоростью работы
декодера Витерби. Это дает возможность использования более
длинных кодов с декодированием алгоритмом Витерби с неполным
переборов ветвей и дальнейшим снижением с помощью МПД
вероятности ошибки до теоретически возможного уровня. Данная
схема будет обладать как высокой скоростью декодирования, так и
высокой его эффективностью, что и требует большинство
современных систем передачи и обработки информации. Дальнейшее
исследование будет посвящено подбору кодов большей длины, выбору
наилучшего числа просматриваемых путей декодером Витерби и
организации двухэтапной схемы декодирования такого кода
декодером Витерби и двоичным несистематическим многопороговым
декодером.
Большой объем разнообразного научного и обучающего материала
по двоичным и недвоичным многопороговым декодерам и другим
методам коррекции ошибок, представлен на специализированном вебсайте www.mtdbest.ru [3].
Работа выполнена при поддержке РФФИ (грант №15-07-06348) и
гранта Президента РФ (грант МД-639.2014.9).
Библиографический список
1. Золотарёв В.В., Овечкин Г.В. Помехоустойчивое кодирование.
Методы и алгоритмы. Справочник – М.: Горячая линия – Телеком,
2004, 126 с.
2. Золотарев В.В. Теория и алгоритмы многопорогового
декодирования // Под редакцией члена-корреспондента РАН
Ю.Б. Зубарева. - М.: «Радио и связь», «Горячая линия – Телеком»,
2006. 276 с.
3. Веб-сайт www.mtdbest.ru.