Алгоритм решения текстовой задачи № Вопросы к задаче

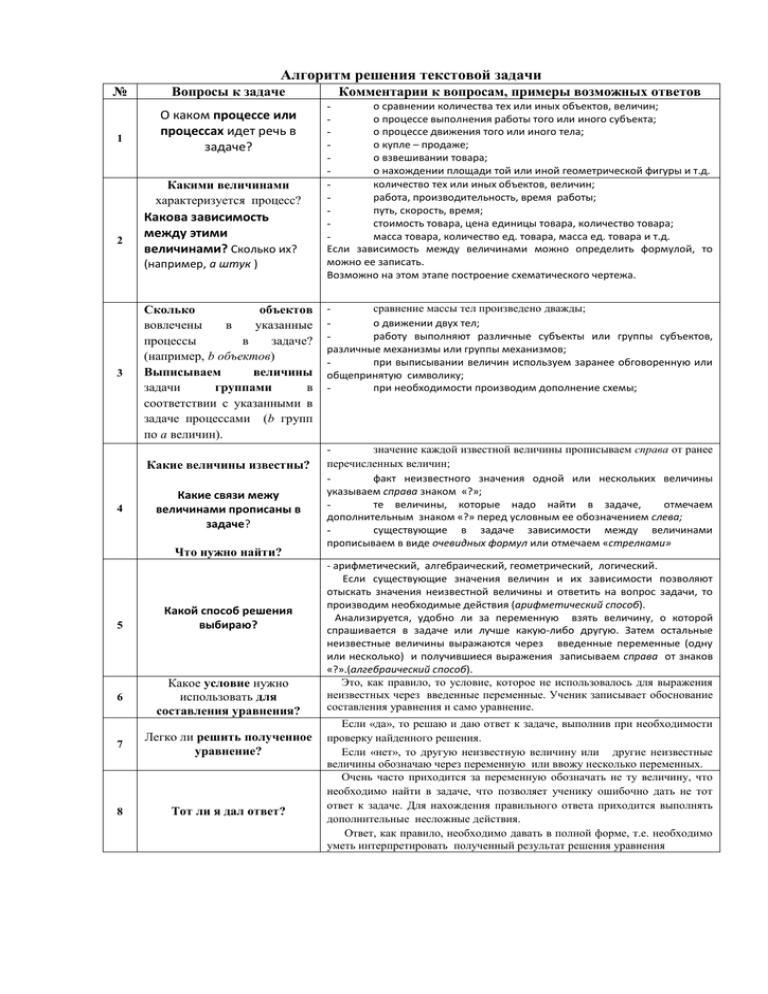
Алгоритм решения текстовой задачи
№
1
Вопросы к задаче
О каком процессе или
процессах идет речь в
задаче?
Какими величинами
характеризуется процесс?
2
Какова зависимость
между этими
величинами? Сколько их?
(например, а штук )
3
Сколько
объектов
вовлечены
в
указанные
процессы
в
задаче?
(например, b объектов)
Выписываем
величины
задачи
группами
в
соответствии с указанными в
задаче процессами (b групп
по а величин).
Какие величины известны?
4
Какие связи межу
величинами прописаны в
задаче?
Что нужно найти?
5
Какой способ решения
выбираю?
6
Какое условие нужно
использовать для
составления уравнения?
7
Легко ли решить полученное
уравнение?
8
Тот ли я дал ответ?
Комментарии к вопросам, примеры возможных ответов
о сравнении количества тех или иных объектов, величин;
о процессе выполнения работы того или иного субъекта;
о процессе движения того или иного тела;
о купле – продаже;
о взвешивании товара;
о нахождении площади той или иной геометрической фигуры и т.д.
количество тех или иных объектов, величин;
работа, производительность, время работы;
путь, скорость, время;
стоимость товара, цена единицы товара, количество товара;
масса товара, количество ед. товара, масса ед. товара и т.д.
Если зависимость между величинами можно определить формулой, то
можно ее записать.
Возможно на этом этапе построение схематического чертежа.
сравнение массы тел произведено дважды;
о движении двух тел;
работу выполняют различные субъекты или группы субъектов,
различные механизмы или группы механизмов;
при выписывании величин используем заранее обговоренную или
общепринятую символику;
при необходимости производим дополнение схемы;
значение каждой известной величины прописываем справа от ранее
перечисленных величин;
факт неизвестного значения одной или нескольких величины
указываем справа знаком «?»;
те величины, которые надо найти в задаче,
отмечаем
дополнительным знаком «?» перед условным ее обозначением слева;
существующие в задаче зависимости между величинами
прописываем в виде очевидных формул или отмечаем «стрелками»
- арифметический, алгебраический, геометрический, логический.
Если существующие значения величин и их зависимости позволяют
отыскать значения неизвестной величины и ответить на вопрос задачи, то
производим необходимые действия (арифметический способ).
Анализируется, удобно ли за переменную взять величину, о которой
спрашивается в задаче или лучше какую-либо другую. Затем остальные
неизвестные величины выражаются через введенные переменные (одну
или несколько) и получившиеся выражения записываем справа от знаков
«?».(алгебраический способ).
Это, как правило, то условие, которое не использовалось для выражения
неизвестных через введенные переменные. Ученик записывает обоснование
составления уравнения и само уравнение.
Если «да», то решаю и даю ответ к задаче, выполнив при необходимости
проверку найденного решения.
Если «нет», то другую неизвестную величину или другие неизвестные
величины обозначаю через переменную или ввожу несколько переменных.
Очень часто приходится за переменную обозначать не ту величину, что
необходимо найти в задаче, что позволяет ученику ошибочно дать не тот
ответ к задаче. Для нахождения правильного ответа приходится выполнять
дополнительные несложные действия.
Ответ, как правило, необходимо давать в полной форме, т.е. необходимо
уметь интерпретировать полученный результат решения уравнения