Математика Ажулаева П.М.

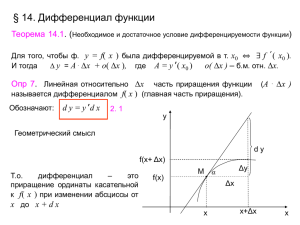
1.
2.
3.
4.
5.
6.
7.
8.
9.
1.
2.
3.
4.
5.
6.
7.
8.
9.
Группа КС- 13
Дисциплина «Элементы высшей математики»
12.02.2015
2-58. Практические занятия № 11 «Вычисление производных»
Задания № 208-212(а, б), 215, 224,225 (в, г) стр. 117, 120
Учебник Алгебра и начала анализа А.Н. Колмогоров
2-60. Применение производной (теория)
Подготовить конспект
Учебник Алгебра и начала анализа А.Н. Колмогоров стр. 137, 143-147
Контрольные вопросы по теме
Критические точки.
Необходимое условие экстремума.
Признак максимума.
Признак минимума.
Признак возрастания, убывания функции. Алгоритм.
Алгоритм вычисления наибольшего и наименьшего значения функции с помощью
производной.
Формулы дифференцирования.
Правила дифференцирования.
Производная в физике и технике.
13.02.2015
2-62. Практические занятия № 12 «Применение производной»
Задания № 268 стр. 141, 281 (а, в), 288 (а, г)
Учебник Алгебра и начала анализа А.Н. Колмогоров
2-64. Исследование и построение графика функции
Учебник Алгебра и начала анализа А.Н. Колмогоров стр. 151- 153 (конспект теории с
примерами исследования).
Контрольные вопросы по теме
Критические точки.
Необходимое условие экстремума.
Признак максимума.
Признак минимума.
Признак возрастания, убывания функции. Алгоритм.
Алгоритм вычисления наибольшего и наименьшего значения функции с помощью
производной.
Формулы дифференцирования.
Правила дифференцирования.
Схема исследования.
14.02.2015
2-66. Практическое занятие № 13 «Исследование и построение графика функции»
Задания № 297 (а, г), № 300 (б, г)
Самостоятельная работа № 10 Расчетно-графическая работа по теме: «Исследование и
построение графика функции» (выполнить на исследование и построение не менее трех
примеров) стр. 154 Учебник Алгебра и начала анализа А.Н. Колмогоров и привести
примеры из других источников.
2-68. Дифференциал функции (теория, конспект, примеры 3-5)
Литература Н. Ш. Кремер «Высшая математика для экономистов» стр. 244-248
2-70. Практическое занятие № 14 Дифференциал. Применение.
Замечание по всем темам и для самостоятельной работы использовать также
учебник Ш. Кремер «Высшая математика для экономистов»
Группа КС- 13
Дисциплина «Элементы высшей математики»
16. 02.2015
4-72. Практическое занятие № 14-15 Дифференциал. Применение.
Дифференциал
Применение дифференциала в приближенных вычислениях
Определение. Дифференциалом функции в некоторой точке x называется главная, линейная часть
приращения функции.
Дифференциал функции y = f(x) равен произведению её производной на приращение независимой
переменной x.
Это записывается так:
𝒅𝒚 = 𝒚′ ∆𝒙 или 𝒅𝒇(𝒙) = 𝒇′ (𝒙)∆𝒙 или же 𝒅𝒇(𝒙) = 𝒇′ (𝒙)𝒅𝒙
Итак, дифференциал функции y = f(x) равен произведению её производной на приращение независимой
переменной.
Геометрический смысл дифференциала
Нарафике функции y=f(x) возьмем произвольную точку M(x;y) и дадим аргументу x приращение ∆𝑥.
При этом функция получит приращение ∆𝑦 (на
рисунке отрезок NM1).
М1
у
Проведем касательную к кривой y=f(x) в точке M и
обозначим угол ее наклона к оси Ox через 𝛼 , тогда
P
М

f x   tg  .
N
Из треугольника

0
х
х+х
х
MNP
находим
PN  MN  tg α 
 Δx tg   f xΔx , т.е. dy  PN
.
Таким образом, дифференциал функции численно равен приращению ординаты касательной, проведенной
к графику функции y=f(x) в данной точке, когда аргумент x получает приращение ∆𝑥.
Пример 1. Найти дифференциалы функций:
1)
;
2)
3)
;
;
4)
.
Применение дифференциала в приближенных вычислениях
Приближенное равенство
или
(1)
позволяет использовать дифференциал для приближенных вычислений значений функции.
Запишем приближенное равенство более подробно.
Так как
то
или
(2)
Пример 1. Пользуясь понятием дифференциала, вычислить приближенно ln 1,01.
Решение. Число ln 1,01 является одним из значений функции y = ln x . Формула (11) в данном
случае примет вид
Положим
тогда
Следовательно,
что является очень хорошим приближением
(табличное значение ln 1,01 = 0,0100).
Пример 2. Пользуясь понятием дифференциала, вычислить приближенно
Решение. Число
1
√1,005
является одним из значений функции 𝑦 =
1
1
1
√1,005
√𝑥
Так как производная этой функции 𝑦 ′ = −
,
2𝑥√𝑥
то формула (11) примет вид
Полагая
и
получаем
(табличное значение
).
Пользуясь приближенным значением числа, можно иметь возможность судить о степени его
точности. С этой целью вычисляют его абсолютную и относительную погрешности.
Абсолютная погрешность
приближенного числа y равна абсолютной величине разности между
точным числом b и его приближенным значением:
(3)
Относительной погрешностью
приближенного числа y называется отношение абсолютной
погрешности этого числа к абсолютной величине соответствующего точного числа:
(4)
Если точное число неизвестно, то
(5)
Иногда, прежде чем применить формулу (11), требуется предварительно преобразовать исходную
величину. Как правило, это делается в двух целях. Во-первых, надо добиться, чтобы величина
была
достаточно малой по сравнению с 𝑓 ′ (x0), так как чем меньше
, тем, вообще говоря, точнее
результат приближенного вычисления. Во-вторых, желательно, чтобы величина f(x0) вычислялась просто.
3
Пример 5. Пользуясь понятием дифференциала, вычислить приближенно √2. Оценить точность
полученного результата.
Самостоятельная работа № 11 расчетная работа по вычислению производных, применение и
дифференциал.
Литература Н. Ш. Кремер «Высшая математика для экономистов» стр. 176 -208; 244-248
выписать примеры с решениями и объяснениями.
17.02.2015
4-76. Интегральное исчисление
Литература Н. Ш. Кремер «Высшая математика для экономистов» стр.251-257 составить
конспект, выписать формулы, правила, свойства и разобраться в примерах, приведенных в
учебнике. Повторить материал первого курса «Первообразная».
18.02.2015
2-78. Методы интегрирования
Литература Н. Ш. Кремер «Высшая математика для экономистов» стр.258-262 составить
конспект, выписать формулы, правила, свойства и разобраться в примерах, приведенных в
учебнике. Повторить материал первого курса «Первообразная».
Группа КС -14
Дисциплина «Математика»
14.02.2015 2-166. Практическое занятие № 42. Решение задач.
Задания № 219, 220, 229 (а, б)
Учебник Л.С. Атанасян стр. 67-68
16.02.2015. 2-168. Пирамида. Тетраэдр. (теория)
Учебник Л.С. Атанасян стр. 69- 71, 24.
17.02.2015. 2-170. ПЗ № 43 Решение задач.
Задания. № 17 стр. 13; 67, 71, стр. 29; 239,241 стр. 72 Учебник Л.С. Атанасян
Самостоятельная работа № 26 Работа с конспектом (дополнение), изготовление модели
фигур, развертки. №271 – 275 – практические задания Стр. 79 Учебник Л.С. Атанасян
Контрольные вопросы
1. Многогранник.
2. Выпуклый, невыпуклый многогранник.
3. Призма.
4. Виды призм.
5. Параллелепипед.
6. Прямоугольный параллелепипед.
7. Пирамида.
8. Усеченная пирамида.
9. Правильные многогранники.
Группа ТЭ -14
Дисциплина «Математика»
14.02.2015 2-166. Практическое занятие № 42. Решение задач.
Задания № 219, 220, 229 (а, б)
Учебник Л.С. Атанасян стр. 67-68
18.02.2015. 2-168. Пирамида. Тетраэдр. (теория)
Учебник Л.С. Атанасян стр. 69- 71, 24.
2-170. ПЗ № 43 Решение задач.
Задания. № 17 стр. 13; 67, 71, стр. 29; 239,241 стр. 72 Учебник Л.С. Атанасян
Самостоятельная работа № 26 Работа с конспектом (дополнение), изготовление модели
фигур, развертки. №271 – 275 – практические задания Стр. 79 Учебник Л.С. Атанасян
Контрольные вопросы
1. Многогранник.
2. Выпуклый, невыпуклый многогранник.
3. Призма.
4. Виды призм.
5. Параллелепипед.
6. Прямоугольный параллелепипед.
7. Пирамида.
8. Усеченная пирамида.
9. Правильные многогранники.