анализ уровня и структуры цен, формируемых каналами
реклама

Óòêèíà Í.Â., Ñåìåðêîâà Ë.Í.
Пензенский государственный университет
ÀÍÀËÈÇ ÓÐÎÂÍß È ÑÒÐÓÊÒÓÐÛ ÖÅÍ, ÔÎÐÌÈÐÓÅÌÛÕ ÊÀÍÀËÀÌÈ
ÐÀÑÏÐÅÄÅËÅÍÈß ÏÐÎÄÓÊÖÈÈ
 ñòàòüå ðàññìàòðèâàþòñÿ âîïðîñû, ñâÿçàííûå ñ ïðîöåññîì öåíîîáðàçîâàíèÿ ïðîèçâîäñòâåííîãî ïðåäïðèÿòèÿ, èñïîëüçóþùåãî êîñâåííûå êàíàëû ðàñïðåäåëåíèÿ. Ïðèâîäÿòñÿ ìàòåìàòè÷åñêàÿ
ìîäåëü è àëãîðèòì ðåøåíèÿ çàäà÷è àíàëèçà óðîâíÿ è ñòðóêòóðû öåí, ôîðìèðóåìûõ êàíàëàìè
ðàñïðåäåëåíèÿ ïðîäóêöèè; ðàññìàòðèâàåòñÿ ïðèìåð ðåøåíèÿ êîíêðåòíîé ïðàêòè÷åñêîé çàäà÷è.
Ââåäåíèå
 óñëîâèÿõ ðûíî÷íîé ýêîíîìèêè îäíîé
èç ãëàâíûõ çàäà÷ óïðàâëåíèÿ ïðîèçâîäñòâåííûì ïðåäïðèÿòèåì ÿâëÿåòñÿ óïðàâëåíèå ñáûòîì âûïóñêàåìîé èì ïðîäóêöèè. ×åì âûøå
ýôôåêòèâíîñòü ñáûòà, òåì ñèëüíåå ó ïðåäïðèÿòèÿ êîíêóðåíòíîå ïðåèìóùåñòâî íà ðûíêå.
Äëÿ êîíêðåòíîãî ïðîèçâîäñòâåííîãî ïðåäïðèÿòèÿ ýôôåêòèâíîñòü ñáûòà çàâèñèò îò ìíîãèõ ôàêòîðîâ, òàêèõ êàê öåíà è êà÷åñòâî âûïóñêàåìîé ïðîäóêöèè, ðàñõîäû íà ðåêëàìó,
âûáîð òîðãîâûõ ïîñðåäíèêîâ, ïðàâèëüíàÿ
îðãàíèçàöèÿ ñåòè ðàñïðåäåëåíèÿ è äðóãèõ.
Ñ÷èòàåòñÿ, ÷òî îäíîé èç íàèáîëåå ðàñïðîñòðàíåííûõ ïðè÷èí íèçêîãî óðîâíÿ ïðîäàæ ïðîäóêöèè ïðîèçâîäñòâåííûõ ïðåäïðèÿòèé ÿâëÿåòñÿ íåñîîòâåòñòâèå ðîçíè÷íûõ öåí
çàÿâëåííîìó ïîçèöèîíèðîâàíèþ [1, 2, 3]. Çàíèæåííàÿ ðîçíè÷íàÿ öåíà ïî ñðàâíåíèþ ñ
îæèäàåìîé çà÷àñòóþ àññîöèèðóåòñÿ ó êîíå÷íûõ ïîòðåáèòåëåé ñ íèçêèì êà÷åñòâîì òîâàðà. Êðîìå òîãî, çàíèæåííàÿ ðîçíè÷íàÿ öåíà
íà ïðîäóêöèþ, âûïóñêàåìóþ ïðåäïðèÿòèåì,
ìîæåò îñëàáèòü èíòåðåñ ó ðîçíè÷íûõ òîðãîâöåâ, òàê êàê óìåíüøàåòñÿ âåëè÷èíà èõ òîðãîâîé íàöåíêè. Çàâûøåííûå ðîçíè÷íûå öåíû
òàêæå íå ñïîñîáñòâóþò óâåëè÷åíèþ îáúåìîâ
ïðîäàæ. Êîíå÷íûé ïîòðåáèòåëü îòêàçûâàåòñÿ îò ïîêóïêè òîâàðà, åñëè íå ìîæåò ñåáå
ïîçâîëèòü êóïèòü åãî ïî ïðåäëàãàåìîé öåíå
èëè ñ÷èòàåò íåöåëåñîîáðàçíûì ïëàòèòü áîëüøèå äåíüãè çà òîâàð ïðè íàëè÷èè àíàëîãè÷íîãî ïî áîëåå íèçêîé öåíå. Ïðè ýòîì çíà÷èòåëüíîå âëèÿíèå íà ïîëèòèêó öåí ïðîèçâîäñòâåííîãî ïðåäïðèÿòèÿ îêàçûâàåò ïîñðåäíè÷åñêàÿ äåÿòåëüíîñòü òîðãîâëè. Ñëåäîâàòåëüíî, äëÿ îáåñïå÷åíèÿ ýôôåêòèâíîãî ñáûòà ðóêîâîäñòâó ïðîèçâîäñòâåííîãî ïðåäïðèÿòèÿ,
èñïîëüçóþùåãî êîñâåííûå êàíàëû ðàñïðåäåëåíèÿ, ñëåäóåò óäåëèòü îñîáîå âíèìàíèå àíàëèçó óðîâíÿ è ñòðóêòóðû íå òîëüêî ðîçíè÷-
&
ВЕСТНИК ОГУ №6(88)/июнь`2008
íûõ öåí, íî è öåí ïåðåïðîäàæè, ôîðìèðóåìûõ êàíàëàìè ðàñïðåäåëåíèÿ.
Òàêèì îáðàçîì, ìîæíî ñäåëàòü âûâîä,
÷òî çàäà÷à àíàëèçà óðîâíÿ è ñòðóêòóðû öåí,
ôîðìèðóåìûõ êàíàëàìè ðàñïðåäåëåíèÿ ïðîäóêöèè, ÿâëÿåòñÿ âàæíîé äëÿ ïðîèçâîäñòâåííîãî ïðåäïðèÿòèÿ.
Ðåøåíèå çàäà÷è àíàëèçà óðîâíÿ è ñòðóêòóðû öåí, ôîðìèðóåìûõ êàíàëàìè ðàñïðåäåëåíèÿ ïðîäóêöèè
Äëÿ ðåøåíèÿ çàäà÷è àíàëèçà óðîâíÿ è
ñòðóêòóðû öåí, ôîðìèðóåìûõ êàíàëàìè ðàñïðåäåëåíèÿ, ïðåäëàãàåòñÿ èñïîëüçîâàòü ïîäõîä, îñíîâàííûé íà ïðèìåíåíèè ìàòåìàòè÷åñêîãî ìîäåëèðîâàíèÿ.
Ìàòåìàòè÷åñêîå ìîäåëèðîâàíèå ïîçâîëÿåò íå òîëüêî ôîðìàëèçîâàòü ýêîíîìè÷åñêîå ÿâëåíèå èëè ïðîöåññ, íî è âûÿâèòü åãî
îñîáåííîñòè [4, ñ. 270]. Êðîìå òîãî, ìàòåìàòè÷åñêèå ìîäåëè èìåþò õîðîøóþ ïðåäñòàâèìîñòü â ÝÂÌ. Ýòî îñîáåííî àêòóàëüíî â íàñòîÿùåå âðåìÿ, êîãäà íà ìíîãèõ êðóïíûõ è
óñïåøíûõ ïðîèçâîäñòâåííûõ ïðåäïðèÿòèÿõ
âíåäðÿþòñÿ èíôîðìàöèîííûå ñèñòåìû ïëàíèðîâàíèÿ èëè óïðàâëåíèÿ, â òîì ÷èñëå è
ñáûòîâîé äåÿòåëüíîñòüþ.
Êàê èçâåñòíî, îñíîâíûìè ýòàïàìè ïðîöåññà ìîäåëèðîâàíèÿ ÿâëÿþòñÿ [5, 6]:
ïîñòàíîâêà çàäà÷è;
ïîñòðîåíèå ìàòåìàòè÷åñêîé ìîäåëè çàäà÷è;
ðàçðàáîòêà èëè âûáîð ìåòîäîâ (èëè àëãîðèòìîâ), ñ ïîìîùüþ êîòîðûõ ìîæíî ðåøèòü çàäà÷ó;
ðåøåíèå çàäà÷è è àíàëèç ïîëó÷åííûõ
ðåçóëüòàòîâ.
Ðàññìîòðèì èõ áîëåå ïîäðîáíî ïðèìåíèòåëüíî ê ðåøåíèþ çàäà÷è àíàëèçà óðîâíÿ è
ñòðóêòóðû öåí, ôîðìèðóåìûõ êàíàëàìè ðàñïðåäåëåíèÿ.
Уткина Н.В., Семеркова Л.Н.
Çàäà÷à àíàëèçà óðîâíÿ è ñòðóêòóðû öåí,
ôîðìèðóåìûõ êàíàëàìè ðàñïðåäåëåíèÿ ïðîäóêöèè, çàêëþ÷àåòñÿ â ðàñ÷åòå õàðàêòåðèñòèê
ïðîöåññà ðàñïðåäåëåíèÿ ïî èçâåñòíûì çíà÷åíèÿì óïðàâëÿåìûõ ïàðàìåòðîâ, ïðè ôèêñèðîâàííîé ñòðóêòóðå ñåòè ðàñïðåäåëåíèÿ1.
 êà÷åñòâå õàðàêòåðèñòèê ïðîöåññà ðàñïðåäåëåíèÿ â äàííîì ñëó÷àå âûñòóïàþò çíà÷åíèÿ
ðåêîìåíäóåìûõ öåí ïðîäàæè äëÿ îïòîâûõ è
ðîçíè÷íûõ òîðãîâûõ ïîñðåäíèêîâ2; â êà÷åñòâå
óïðàâëÿåìûõ ïàðàìåòðîâ öåëåñîîáðàçíî èñïîëüçîâàòü îïòîâóþ öåíó ïðîèçâîäèòåëÿ è çàïëàíèðîâàííûé èì îáúåì ïðîäàæ (èëè îáúåì
ïðîèçâîäñòâà) êîíêðåòíîãî âèäà ïðîäóêöèè.
 êà÷åñòâå ìàòåìàòè÷åñêîãî îïèñàíèÿ
ñåòè ðàñïðåäåëåíèÿ ïðîäóêöèè â ðàáîòàõ [7,
8] ïðåäëîæåíî èñïîëüçîâàòü ãðàô ïîòîêà òîâàðîâ3 (ÃÏÒ). Ôîðìàëüíî ãðàô ïîòîêà òîâàðîâ G = ( V, A ) îïðåäåëÿåòñÿ íåïóñòûì êîíå÷íûì ìíîæåñòâîì À äóã è îòîáðàæåíèåì ∆
ìíîæåñòâà À íà V × V .
Ñðåäè ìíîæåñòâà âåðøèí V ãðàôà G âûäåëÿþòñÿ äâà íåïåðåñåêàþùèõñÿ ïîäìíîæåñòâà
V' è V' ' ' âåðøèí. Âåðøèíàì δ i ñ îòðèöàòåëüíîé
ñòåïåíüþ σ − ( δ i ) = 0 ñòàâÿòñÿ â ñîîòâåòñòâèå
ïðîèçâîäèòåëè òîâàðîâ. Âåðøèíàì δ j ñ ïîëîæèòåëüíîé ñòåïåíüþ σ + ( δ j ) = 0 ñòàâÿòñÿ â ñîîòâåòñòâèå êîíå÷íûå ïîòðåáèòåëè òîâàðîâ. Êàæäîé âåðøèíå δ r èç ïîäìíîæåñòâà
V' ' = V /( V'∪V' ' ' ) ñîîòâåòñòâóåò ïîñðåäíèê. Äóãàì ãðàôà G ñîîòâåòñòâóþò õîçÿéñòâåííûå ñâÿçè, óñòàíàâëèâàåìûå ìåæäó ó÷àñòíèêàìè ïðîöåññà ðàñïðåäåëåíèÿ; ïðîïóñêíàÿ ñïîñîáíîñòü c ij äóãè a ij èíòåðïðåòèðóåòñÿ êàê ìàêñèìàëüíîå êîëè÷åñòâî òîâàðîâ, êîòîðîå ìîæåò
áûòü ïðîäàíî i-ì ó÷àñòíèêîì ïðîöåññà ðàñïðåäåëåíèÿ (èëè êóïëåíî j-ì ó÷àñòíèêîì) â ðåçóëüòàòå óñòàíîâëåíèÿ ìåæäó íèìè õîçÿéñòâåííîé
ñâÿçè íà íåêîòîðûé ïåðèîä âðåìåíè.
Äëÿ îòîáðàæåíèÿ õîçÿéñòâåííûõ ñâÿçåé
âîñïîëüçóåìñÿ ìàòðèöåé PR, ðàññìîòðåííîé
â ðàáîòå [9]. Çíà÷åíèÿ ýëåìåíòîâ ìàòðèöû PR
èíòåðïðåòèðóþòñÿ êàê ñòåïåíè ïðåäïî÷òåíèÿ
óñòàíîâëåíèÿ õîçÿéñòâåííûõ ñâÿçåé ìåæäó
ó÷àñòíèêàìè ïðîöåññà ðàñïðåäåëåíèÿ â íåêîòîðûé ïåðèîä âðåìåíè. Òàêèì îáðàçîì, ãðàô
Анализ уровня и структуры цен...
ïîòîêà òîâàðîâ ÿâëÿåòñÿ íå÷åòêèì ãðàôîì G = ( V, A ) [10, ñ. 55], òàê êàê óäîâëåòâîðÿåò
~
âûðàæåíèþ:
(1)
∀( δ i , δ j ) ∈ V × V : µ G ( δ i , δ j ) ∈ M ,
ãäå µ G ( δ i , δ j ) ôóíêöèÿ ïðèíàäëåæíîñòè äóãè
a ij , ñîåäèíÿþùåé âåðøèíû δ i è δ j , ãðàôó G;
M ìíîæåñòâî ïðèíàäëåæíîñòåé ýëåìåíòîâ
ìíîæåñòâà V × V .
 íàñòîÿùåå âðåìÿ åùå íåäîñòàòî÷íî
õîðîøî ðàçðàáîòàíû ôîðìàëèçîâàííûå ìåòîäû ïîèñêà ðåøåíèé íà íå÷åòêèõ ãðàôàõ.
Ïîýòîìó öåëåñîîáðàçíî ïåðåéòè îò íå÷åòêîãî îïèñàíèÿ ñåòè ðàñïðåäåëåíèÿ ê òî÷íîìó
åå ïðåäñòàâëåíèþ. Äëÿ ýòîãî âîñïîëüçóåìñÿ
ïîíÿòèåì ïîðîãà ðàçäåëåíèÿ [11]. Â äàííîì
ñëó÷àå ïîðîã ðàçäåëåíèÿ γ öåëåñîîáðàçíî
îãðàíè÷èòü óñëîâèåì:
~
~
γ < min
max min[µ A ( δ j , δ i ), µ A ( δ j , δ r )], (2)
ir
i
δj
i
ãäå µ A ( δ j , δ i ) , µ A ( δ j , δ r ) ýëåìåíòû ìàòðèöû PR.
Åñëè ïîðîã γ âûáðàí, òî ñîãëàñíî òåîðåìå îá îòäåëèìîñòè [11] äëÿ i-ãî ó÷àñòíèêà
ïðîöåññà ðàñïðåäåëåíèÿ öåëåñîîáðàçíî óñòàíàâëèâàòü õîçÿéñòâåííûå ñâÿçè ñ äðóãèìè
ó÷àñòíèêàìè ïðîöåññà ðàñïðåäåëåíèÿ, êîòîðûå îáðàçóþò óðîâíåâîå ìíîæåñòâî M i :
i
i
M i = {δ j | µ A ( δ j ) ≥ γ} äëÿ âñåõ δ j ∈ M i .
(3)
Äðóãèìè ñëîâàìè, ìåæäó âåðøèíàìè
δ i ∈ V è δ j ∈ V ãðàôà G äóãà a ij óñòàíàâëèâàåòñÿ, åñëè µ G ( δ i , δ j ) ≥ γ .
Äëÿ ïîëó÷åíèÿ êîëè÷åñòâåííûõ õàðàêòåðèñòèê êàæäîé õîçÿéñòâåííîé ñâÿçè èñïîëüçóåòñÿ ïîíÿòèå ïîòîêà òîâàðîâ íà äóãå ãðàôà.
Ïîòîêîì òîâàðîâ âåëè÷èíû υ èç V' â V ' ' ' áóäåì íàçûâàòü ôóíêöèþ ξ , îòîáðàæàþùóþ
ìíîæåñòâî A â ìíîæåñòâî íåîòðèöàòåëüíûõ
÷èñåë è óäîâëåòâîðÿþùóþ óñëîâèÿì [12, 13]:
(4)
ξ( δ i , V ) − ξ( V, δ i ) = υ äëÿ δ i ∈ V' ,
i
~
ξ( δ i , V ) − ξ( V, δ i ) = 0 äëÿ δ i ∈ V' ' ,
(5)
ξ( δ i , V ) − ξ( V, δ i ) = −υ äëÿ δ i ∈ V' ' ' ,
(6)
0 ≤ ξ( δ i , δ j ) ≤ c( δ i , δ j ) äëÿ ( δ i , δ j ) ∈ A ,
(7)
Âåëè÷èíà ξ( δ i , V ) íàçûâàåòñÿ çíà÷åíèåì
ïîòîêà òîâàðîâ ïî äóãå [12, 13], èñõîäÿùåé
Ïîä ñåòüþ ðàñïðåäåëåíèÿ ïîíèìàåòñÿ ñîâîêóïíîñòü êàíàëîâ ðàñïðåäåëåíèÿ ïðåäïðèÿòèÿ, èñïîëüçóåìàÿ äëÿ ðàñïðåäåëåíèÿ èì íåêîòîðîãî âèäà îäíîðîäíîé ïðîäóêöèè íà íåêîòîðîé çàäàííîé òåððèòîðèè.
Ðå÷ü èäåò èìåííî î ðåêîìåíäóåìûõ öåíàõ ïðîäàæè ïðîäóêöèè, ïîñêîëüêó ïðîèçâîäèòåëþ þðèäè÷åñêè çàïðåùåíî
äèêòîâàòü öåíû òîðãîâûì îðãàíèçàöèÿì.
3
 êîíòåêñòå ðàáîòû ïîíÿòèÿ «òîâàð» è «ïðîäóêöèÿ» ðàññìàòðèâàþòñÿ êàê ðàâíîçíà÷íûå.
1
2
ВЕСТНИК ОГУ №6(88)/июнь`2008
&!
Экономические науки
èç âåðøèíû δ i , è ñîäåðæàòåëüíî èíòåðïðåòèðóåòñÿ êàê êîëè÷åñòâî îäíîðîäíîé ïðîäóêöèè, ðàñïðåäåëÿåìîé ìåæäó ó÷àñòíèêàìè
ïðîöåññà ðàñïðåäåëåíèÿ ïîñðåäñòâîì óñòàíîâëåíèÿ ìåæäó íèìè õîçÿéñòâåííîé ñâÿçè,
îòîáðàæàåìîé â ãðàôå G äàííîé äóãîé.
Èñïîëüçóåòñÿ ïîíÿòèå êîýôôèöèåíòà
òîðãîâîé íàöåíêè [1, 2, 3]. Çíà÷åíèå k ij îïðåäåëÿåòñÿ êàê âåñ äóãè a ij è â îáùåì ñëó÷àå
ìîæåò áûòü ôóíêöèåé âåñà y i âåðøèíû δ i , ò.å.
k ij = f ij ( y i ) [14]. Âåñ ëþáîé âåðøèíû ÃÏÒ ÿâëÿåòñÿ ôóíêöèåé âåñîâ âñåõ âåðøèí, ñîîòâåòñòâóþùèõ íà÷àëüíûì âåðøèíàì äóã, êîòîðûå çàêàí÷èâàþòñÿ â äàííîé âåðøèíå. Íàïðèìåð, âåñ y r âåðøèíû δ r ∈ V' ' îïðåäåëÿåòñÿ
êàê y r = f r ( k ir ,..., k nr ) , ãäå k ir ,..., k nr âåñà äóã,
ïîëîæèòåëüíî èíöèäåíòíûõ âåðøèíå δ r .
Ïðèñâàèâàÿ âåðøèíàì èç ïîäìíîæåñòâà V'
îïðåäåëåííûå çíà÷åíèÿ âåñîâ è ïîñëåäîâàòåëüíî âû÷èñëÿÿ âåñà ñâÿçàííûõ ñ íèìè âåðøèí, ìîæíî îïðåäåëèòü âåñà âåðøèí èç ïîäìíîæåñòâà V' ' ' .  îáùåì ñëó÷àå ñâÿçü ìåæäó
âåðøèíàìè ìîæåò áûòü ïðåäñòàâëåíà â ëþáîé ôóíêöèîíàëüíîé ôîðìå.  äàííîé ðàáîòå ðàññìàòðèâàåòñÿ ñëó÷àé ïðåäñòàâëåíèÿ
ñâÿçè â ôîðìå ëèíåéíûõ îòíîøåíèé.
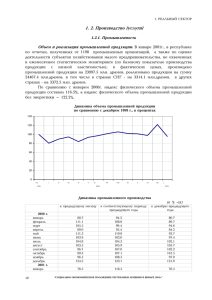
Íà ðèñóíêå 1 ïðèâåäåí ïðèìåð îïèñàíèÿ
ñåòè ðàñïðåäåëåíèÿ ïðîäóêöèè íåêîòîðîãî
àáñòðàêòíîãî ïðîèçâîäñòâåííîãî ïðåäïðèÿòèÿ â âèäå ÃÏÒ.
Äëÿ ðåøåíèÿ çàäà÷è àíàëèçà óðîâíÿ è
ñòðóêòóðû öåí ïðîäàæè ïðîäóêöèè, ôîðìèðóåìûõ êàíàëàìè ðàñïðåäåëåíèÿ, ñòðîèòñÿ
ìàòðèöà êîýôôèöèåíòîâ òîðãîâûõ íàöåíîê K = k ij ðàçìåðíîñòè n × n , ãäå n ÷èñëî
δ1 ' ' '
k4
δ1 ' '
k5
k1
δ1 '
k2
δ2''
k6
δ 2 '''
k9
δ4''
δ3 ' ' '
k10
k11
δ5 ' '
k12
k3
δ3 ''
δ4 '' '
δ5 ' ' '
k7
k8
δ6 ' ''
δ7 '' '
Ðèñóíîê 1. Ãðàô ïîòîêà òîâàðîâ
&"
ВЕСТНИК ОГУ №6(88)/июнь`2008
âåðøèí ÃÏÒ, êîòîðóþ îïðåäåëèì ñëåäóþùèì îáðàçîì. Ýëåìåíò k ij ìàòðèöû K ðàâåí
êîýôôèöèåíòó òîðãîâîé íàöåíêè ñîîòâåòñòâóþùåé õîçÿéñòâåííîé ñâÿçè, îòîáðàæàåìîé â ãðàôå äóãîé a ij . Âåëè÷èíà êîýôôèöèåíòà òîðãîâîé íàöåíêè k ij çàâèñèò îò öåíû ïðîäàæè è êîëè÷åñòâà ïðîäàâàåìîé ïðîäóêöèè
è âû÷èñëÿåòñÿ ïî ôîðìóëå:
k ij =
x i + ω( ξ ij )
= 1+
ω( ξ ij )
,
(8)
xi
xi
ãäå x i öåíà ïðîäàæè, õàðàêòåðèñòèêà âåðøèíû δ i ; ωij ( ξ ij ) ôóíêöèÿ ïîòîêà òîâàðîâ
ïî äóãå a ij .
Åñëè äóãà a ij íå ñóùåñòâóåò, òî ïðåäïîëàãàåòñÿ, ÷òî k ij = 0 . Äëÿ ñåòè ðàñïðåäåëåíèÿ,
ïðåäñòàâëåííîé ÃÏÒ íà ðèñóíêå 1, ìàòðèöà
K èìååò âèä:
0 k1
k2
k3
0
0
0
0
0
0
0
0
0
0
0
0
0
k5
0
k4
0
0
0
0
0
0
0
0
0
0
0
k6
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
k7
k8
0
0
0
0
0
0
0
k9
0
0
0
0
0
0
K= 0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
k 10
0
k 11
0
k 12
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0.
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
Èñïîëüçóåòñÿ ïîíÿòèå êàíàëà ðàñïðåäåëåíèÿ (êàíàëà ñáûòà) [1, 3], êîòîðîìó â ÃÏÒ
ñîîòâåòñòâóåò ïóòü. Ïóòü íà ÃÏÒ îïðåäåëÿåòñÿ êàê óïîðÿäî÷åííàÿ ïîñëåäîâàòåëüíîñòü
äóã, ñîåäèíÿþùèõ âåðøèíó δ i ñ âåðøèíîé δ j .
Êîýôôèöèåíò òîðãîâîé íàöåíêè, ñîçäàâàåìûé êàíàëîì ñáûòà, îïðåäåëÿåòñÿ êàê ïðîèçâåäåíèå êîýôôèöèåíòîâ òîðãîâûõ íàöåíîê
ñîîòâåòñòâóþùèõ õîçÿéñòâåííûõ ñâÿçåé, êîòîðûå îáðàçóþò äàííûé êàíàë ñáûòà. Â ýòîì
ñëó÷àå çíà÷åíèå âåñà y j ëþáîé âåðøèíû
δ j ∈ ( V' '∪V' ' ' ) ÷åðåç çíà÷åíèÿ êîýôôèöèåíòîâ
òîðãîâûõ íàöåíîê k ij è âåñîâ x i âåðøèí δ i ∈ V'
ìîæíî îïðåäåëèòü ñëåäóþùèì îáðàçîì
n
L
i =1
l =1
y j = ∑ x i ⋅ ∑ k lij ,
(9)
ãäå x i âåñ âåðøèíû, i = 1,2,..., n ; k lij êîýôôèöèåíò òîðãîâîé íàöåíêè, ñîçäàâàåìûé êàíà-
Уткина Н.В., Семеркова Л.Н.
Анализ уровня и структуры цен...
ëîì ñáûòà, êîòîðîìó ñîîòâåòñòâóåò ïóòü l îò
âåðøèíû δ i ê âåðøèíå δ j , l = 1, 2,..., L.  äàííîì ñëó÷àå L îïðåäåëÿåò ÷èñëî ïóòåé îò âåðøèíû δ i ê âåðøèíå δ j .
Âûðàæåíèå (9) ìîæåò áûòü ïîëó÷åíî ïî
ìàòðèöå êîýôôèöèåíòîâ òîðãîâûõ íàöåíîê
K ñëåäóþùèì îáðàçîì. Îïðåäåëèì ìàòðèöó
K L = k L ij êîýôôèöèåíòîâ òîðãîâûõ íàöåíîê,
ñîçäàâàåìûõ êàíàëàìè ñáûòà, îáðàçóþùèìè
ñåòü ðàñïðåäåëåíèÿ ïðîäóêöèè ïðåäïðèÿòèÿ.
Ñòðîêè è ñòîëáöû ìàòðèöû K L = k L ij ñîîòâåòñòâóþò âåðøèíàì ÃÏÒ. Ýëåìåíò k L ij ìàòðèöû K L ðàâåí ñóììå êîýôôèöèåíòîâ òîðãîâûõ íàöåíîê âñåõ êàíàëîâ ñáûòà, óñòàíîâëåííûõ ìåæäó i-ì è j-ì ó÷àñòíèêàìè ïðîöåññà
ðàñïðåäåëåíèÿ ïðîäóêöèè. Ìàòðèöà K L ìîæåò áûòü íàéäåíà ïî ìàòðèöå K èç ñëåäóþùèõ ðåêóððåíòíûõ ñîîòíîøåíèé:
K L 1 = K;
K L 2 = K L1 + K × K = K L1 + K 2 ;
K L 3 = K L 2 + K 3;
...
K L n = K L n −1 + K n .
(10)
Êîíåö ïðîöåññà íàñòóïàåò ïðè K n = 0 .
Îòìåòèì íåêîòîðûå ñâîéñòâà ìàòðèöû
K L , ñóùåñòâåííûå ïðè àíàëèçå ïðîöåññà ðàñïðåäåëåíèÿ ïðîäóêöèè, âûïóñêàåìîé ïðåäïðèÿòèåì. Êàê óæå îòìå÷àëîñü, ýëåìåíò k L ij
îïðåäåëÿåòñÿ êàê ñóììà êîýôôèöèåíòîâ òîðãîâûõ íàöåíîê, ñîçäàâàåìûõ êàíàëàìè ñáûòà
ñåòè ðàñïðåäåëåíèÿ ïðîäóêöèè ïðåäïðèÿòèÿ,
êîòîðûì â ÃÏÒ ñîîòâåòñòâóþò ïóòè îò âåðøèíû ñ íîìåðîì i ê âåðøèíå ñ íîìåðîì j. Ïî
ìàòðèöå K L ìîæíî îïðåäåëèòü âåñ ëþáîé âåðøèíû δ j ∈ ( V' '∪V' ' ' ) ïðè çàäàííûõ çíà÷åíèÿõ
âåñîâ âåðøèí èç ïîäìíîæåñòâà V' , ò.å. îïðåäåëèòü çíà÷åíèå ðåêîìåíäóåìîé öåíû ïðîäàæè ïðîäóêöèè, óñòàíàâëèâàåìîé ïðîèçâîäèòåëåì äëÿ êàæäîãî òîðãîâîãî ïîñðåäíèêà (îïòîâîãî è/èëè ðîçíè÷íîãî), âõîäÿùåãî â ñåòü
ðàñïðåäåëåíèÿ, ïðè çàäàííîì çíà÷åíèè îïòîâîé öåíû òîâàðîïðîèçâîäèòåëÿ. Âåñ âåðøèíû δ j â ýòîì ñëó÷àå ðàâåí ñóììå ïðîèçâåäåíèé âåñîâ âåðøèí δ i (i = 1, 2..., n) íà âåñà äóã,
ñîåäèíÿþùèõ âåðøèíó èç ïîäìíîæåñòâà V' ñ
âåðøèíîé δ j . Òàê, äëÿ ðàññìàòðèâàåìîãî ïðèìåðà (ðèñóíîê 1) çíà÷åíèå ïàðàìåòðà x' ' ' 2 îïðåäåëÿåòñÿ âûðàæåíèåì
(11)
x ' ' ' 2 = ( k 1 k 5 k 9 )x ' 1 .
Ñîäåðæàòåëüíûé ñìûñë âûðàæåíèÿ (11)
ñîñòîèò â ñëåäóþùåì: êîíå÷íûé ïîêóïàòåëü,
êîòîðîìó â ÃÏÒ ñîîòâåòñòâóåò âåðøèíà δ' ' ' 2 ,
áóäåò ïîêóïàòü ïðîäóêöèþ ïî öåíå, êîòîðàÿ
ïîìèìî îïòîâîé öåíû òîâàðîïðîèçâîäèòåëÿ âêëþ÷àåò òîðãîâûå íàöåíêè îïòîâîãî è
ðîçíè÷íîãî ïîñðåäíèêîâ (âåðøèíû δ' '1 è δ' ' 4 ).
Òàêèì îáðàçîì, äëÿ êîíêðåòíîãî (àáñòðàêòíîãî) ïðîèçâîäñòâåííîãî ïðåäïðèÿòèÿ,
èìåþùåãî íà íåêîòîðîé çàäàííîé òåððèòîðèè
ñåòü ðàñïðåäåëåíèÿ âûïóñêàåìîé èì ïðîäóêöèè, ïðåäñòàâëåííîé ÃÏÒ (ðèñóíîê 1), ðåøåíà çàäà÷à àíàëèçà óðîâíÿ è ñòðóêòóðû öåí
ïðîäàæè ïðîäóêöèè êàê äëÿ êîíå÷íûõ, òàê è
äëÿ ïðîìåæóòî÷íûõ ïîêóïàòåëåé (ò.å. òîðãîâûõ ïîñðåäíèêîâ, âõîäÿùèõ â ñåòü ðàñïðåäåëåíèÿ). Ñëåäîâàòåëüíî, óñòàíàâëèâàÿ îïòîâóþ
öåíó è ðåêîìåíäóÿ òîðãîâûå íàöåíêè ñâîèì
ïîñðåäíèêàì, ïðîèçâîäñòâåííîå ïðåäïðèÿòèå
ìîæåò ðåãóëèðîâàòü êîíå÷íûå öåíû ïðîäàæè
íà âûïóñêàåìóþ èì ïðîäóêöèþ.
Çàêëþ÷åíèå
 ñèòóàöèè, êîãäà ñòðàòåãè÷åñêèé ìàðêåòèíã êîìïàíèè äîñòàòî÷íî ðàçâèò, â ðåçóëüòàòå ÷åãî îíà èìååò íåêîòîðóþ âëàñòü íàä
ðûíêîì, íàçíà÷åíèå êîíå÷íîé öåíû íà âûïóñêàåìóþ ïðîäóêöèþ ñòàíîâèòñÿ îäíèì èç íàèáîëåå âàæíûõ ðåøåíèé, â çíà÷èòåëüíîé ñòåïåíè îïðåäåëÿþùèõ óñïåõ ñòðàòåãèè. Êîíå÷íàÿ öåíà ïðîäàæè íå òîëüêî âëèÿåò íà óðîâåíü ñïðîñà, íî è âîçäåéñòâóåò íà îáùåå âîñïðèÿòèå òîâàðà êîíå÷íûìè ïîòðåáèòåëÿìè è
ÿâëÿåòñÿ îäíèì èç ôàêòîðîâ, îïðåäåëÿþùèõ
èìèäæ òîðãîâîé ìàðêè ïðîèçâîäèòåëÿ.
Äî íåäàâíåãî âðåìåíè íà îòå÷åñòâåííûõ
ïðîèçâîäñòâåííûõ ïðåäïðèÿòèÿõ ðåøåíèÿ î
öåíîîáðàçîâàíèè ðàññìàòðèâàëèñü èñêëþ÷èòåëüíî ñ ôèíàíñîâûõ ïîçèöèé, à ñàìè öåíû
îïðåäåëÿëèñü â îñíîâíîì â ðàìêàõ îãðàíè÷åíèé ïî çàòðàòàì è ïðèáûëè. Ñ èçìåíåíèåì
ýêîíîìè÷åñêîé è êîíêóðåíòíîé ñèòóàöèè èçìåíèëñÿ è ïîäõîä ê öåíîîáðàçîâàíèþ.  ÷àñòíîñòè, íà ïîëèòèêó öåí ïðîèçâîäñòâåííûõ
ïðåäïðèÿòèé âñå áîëüøå îêàçûâàåò âëèÿíèå
ïîñðåäíè÷åñêàÿ äåÿòåëüíîñòü òîðãîâëè.
Âñëåäñòâèå ÷åãî ïðîâåäåíèå àíàëèçà óðîâíÿ
è ñòðóêòóðû íå òîëüêî êîíå÷íûõ öåí, íî è öåí
ïåðåïðîäàæè, ôîðìèðóåìûõ êàíàëàìè ðàñВЕСТНИК ОГУ №6(88)/июнь`2008
&#
Экономические науки
ïðåäåëåíèÿ ïðîäóêöèè, èìååò äëÿ ïðîèçâîäñòâåííîãî ïðåäïðèÿòèÿ îãðîìíîå çíà÷åíèå.
 ñòàòüå ðàññìàòðèâàåòñÿ çàäà÷à àíàëèçà
óðîâíÿ è ñòðóêòóðû öåí, ôîðìèðóåìûõ êàíàëàìè ðàñïðåäåëåíèÿ ïðîäóêöèè. Äëÿ ðåøåíèÿ
çàäà÷è ïðåäëîæåí ïîäõîä, îñíîâàííûé íà ïðèìåíåíèè ìàòåìàòè÷åñêîãî ìîäåëèðîâàíèÿ.
Õîòÿ ðàññìîòðåíà îäíîïðîäóêòîâàÿ çàäà÷à, ìåòîäîëîãèþ ìîæíî îáîáùèòü íà
ìíîãîïðîäóêòîâóþ ìîäåëü. Êðîìå òîãî,
äàííûé ïîäõîä ìîæíî ïðèìåíÿòü äëÿ èññëåäîâàíèÿ áîëåå ñëîæíûõ ïðîáëåì, íàïðèìåð
äëÿ âû÷èñëåíèÿ ïðåäåëüíûõ çíà÷åíèé òîðãîâûõ íàöåíîê, óñòàíàâëèâàåìûõ â ïðîöåññå ðàñïðåäåëåíèÿ ñîöèàëüíî çíà÷èìûõ òîâàðîâ; äëÿ îïðåäåëåíèÿ îïòîâûõ öåí ïðîèçâîäèòåëÿ â ñèòóàöèè, êîãäà êîíå÷íàÿ öåíà
íà âûïóñêàåìóþ èì ïðîäóêöèþ óñòàíàâëèâàåòñÿ íå ïðîèçâîäèòåëåì, à òîðãîâûìè ïîñðåäíèêàìè. Òàêæå äàííûé ïîäõîä ìîæíî
ïðèìåíÿòü äëÿ àíàëèçà ïðîöåññà öåíîîáðàçîâàíèÿ íå òîëüêî îòäåëüíîãî ïðîèçâîäñòâåííîãî ïðåäïðèÿòèÿ, íî è íåêîòîðîé îòðàñëè â öåëîì.
Ñïèñîê èñïîëüçîâàííîé ëèòåðàòóðû:
1. Ëàìáåí Æàí-Æàê. Ìåíåäæìåíò, îðèåíòèðîâàííûé íà ðûíîê / Ïåðåâ. ñ àíãë. ïîä ðåä. Â.Á. Êîë÷àíîâà. ÑÏá.: Ïèòåð,
2004. 800 ñ.
2. Áàãèåâ Ã.Ë., Òàðàñåâè÷ Â.Ì., Àíí Õ. Ìàðêåòèíã: Ó÷åáíèê. 2-å èçä. Ì.: ÇÀÎ «Èçäàòåëüñòâî «Ýêîíîìèêà», 2001. 703 ñ.
3. Ãîëüäøòåéí Ã.ß., Êàòàåâ À.Â. Ìàðêåòèíã: Ó÷åáíîå ïîñîáèå äëÿ ìàãèñòðàíòîâ. - Òàãàíðîã: Èçä-âî ÒÐÒÓ, 1999.
4. Øîêîðîâà Í.Â. Ìîäåëèðîâàíèå êàê ìåòîä èçó÷åíèÿ ýêîíîìè÷åñêèõ ñèñòåì // Àêòóàëüíûå ïðîáëåìû ýêîíîìèêè, îðãàíèçàöèè è óïðàâëåíèÿ â óñëîâèÿõ ðàçâèòèÿ ïðîèçâîäñòâåííûõ ñèñòåì: Ìàòåðèàëû ìåæäóíàðîäíîé íàó÷íî-ïðàêòè÷åñêîé êîíôåðåíöèè / Ïîä îáù. ðåä. ä.ý.í., ïðîô. Á.Á. Õðóñòàëåâà Ïåíçà: ÏÃÓÀÑ, 2004. - Ñ. 269 - 272.
5. Àáëàíñêàÿ Ë.Â. Ýêîíîìèêî-ìàòåìàòè÷åñêîå ìîäåëèðîâàíèå: ó÷åáíèê / Ïîä îáù. ðåä. È.Í. Äðîãîáûöêîãî. 2-å èçä.,
ñòåðåîòèï. Ì.: Èçäàòåëüñòâî «Ýêçàìåí», 2006. 798 ñ.
6. Øåëîáàåâ Ñ.È. Ìàòåìàòè÷åñêèå ìåòîäû è ìîäåëè. Ì.: ÞÍÈÒÈ, 2000. 367 ñ.
7. Óòêèíà Í.Â. Ñòðóêòóðíî-ïàðàìåòðè÷åñêàÿ îïòèìèçàöèÿ ñåòè ðàñïðåäåëåíèÿ ïðîäóêöèè ïðåäïðèÿòèÿ // Ïðîáëåìû óïðàâëåíèÿ ýêîíîìèêîé â òðàíñôîðìèðóåìîì îáùåñòâå: ñáîðíèê ñòàòåé III Âñåðîññèéñêîé íàó÷íî-ïðàêòè÷åñêîé êîíôåðåíöèè. Ïåíçà: ÏÄÇ, 2006. - Ñ. 97 - 99.
8. Óòêèíà Í.Â. Ìàòåìàòè÷åñêàÿ ìîäåëü ñåòè ðàñïðåäåëåíèÿ òîâàðíûõ ðåñóðñîâ ïðåäïðèÿòèÿ // Ìàòåìàòè÷åñêîå è êîìïüþòåðíîå ìîäåëèðîâàíèå åñòåñòâåííîíàó÷íûõ è ñîöèàëüíûõ ïðîáëåì: ñáîðíèê ñòàòåé I Ìåæäóíàðîäíîé íàó÷íîòåõíè÷åñêîé êîíôåðåíöèè ìîëîäûõ ñïåöèàëèñòîâ, àñïèðàíòîâ è ñòóäåíòîâ. Ïåíçà: ÏÄÇ, 2007. - Ñ. 124 - 126.
9. Óòêèíà Í.Â. Ìîäåëü ðàñïðåäåëåíèÿ òîâàðíûõ ðåñóðñîâ ñ èñïîëüçîâàíèåì íå÷åòêî-ìíîæåñòâåííîãî ïîäõîäà // XXI
âåê: èòîãè ïðîøëîãî è ïðîáëåìû íàñòîÿùåãî. Ìåæâóçîâñêèé ñáîðíèê íàó÷íûõ òðóäîâ. Âûïóñê 8 / Ïîä îáùåé ðåäàêöèåé Ñ.Í. Âîëêîâà. Ïåíçà, Èçä-âî ÏÃÒÀ, 2006. - Ñ. 211 - 214.
10. Êîôìàí À. Ââåäåíèå â òåîðèþ íå÷åòêèõ ìíîæåñòâ: Ïåð ñ ôðàíö. - Ì.: Ðàäèî è ñâÿçü, 1982. - 432 ñ.
11. Íå÷åòêèå ìíîæåñòâà è òåîðèÿ âîçìîæíîñòåé. Ïîñëåäíèå äîñòèæåíèÿ. Ïåð. ñ àíãë. / Ïîä ðåä. Ð.Ð. ßãåðà. - Ì.: Ðàäèî
è ñâÿçü, 1986. - 408 ñ.
12. Ôîðä Ë.Ð., Ôàëêåðñîí Ä.Ð. Ïîòîêè â ñåòÿõ. - Ì.: Ìèð, 1966. - 276 ñ.
13. Õó Ò. Öåëî÷èñëåííîå ïðîãðàììèðîâàíèå è ïîòîêè â ñåòÿõ. - Ì.: Ìèð, 1974. - 520 ñ.
14. Áàñàêåð Ð., Ñààòè Ò. Êîíå÷íûå ãðàôû è ñåòè. - Ì.: Èçä-âî «Íàóêà», 1973. 368 ñ.
Ñòàòüÿ ðåêîìåíäîâàíà ê ïóáëèêàöèè 20.03.08
&$
ВЕСТНИК ОГУ №6(88)/июнь`2008