111 Рис. 1. – Динамика дохода отрасли связи России
реклама
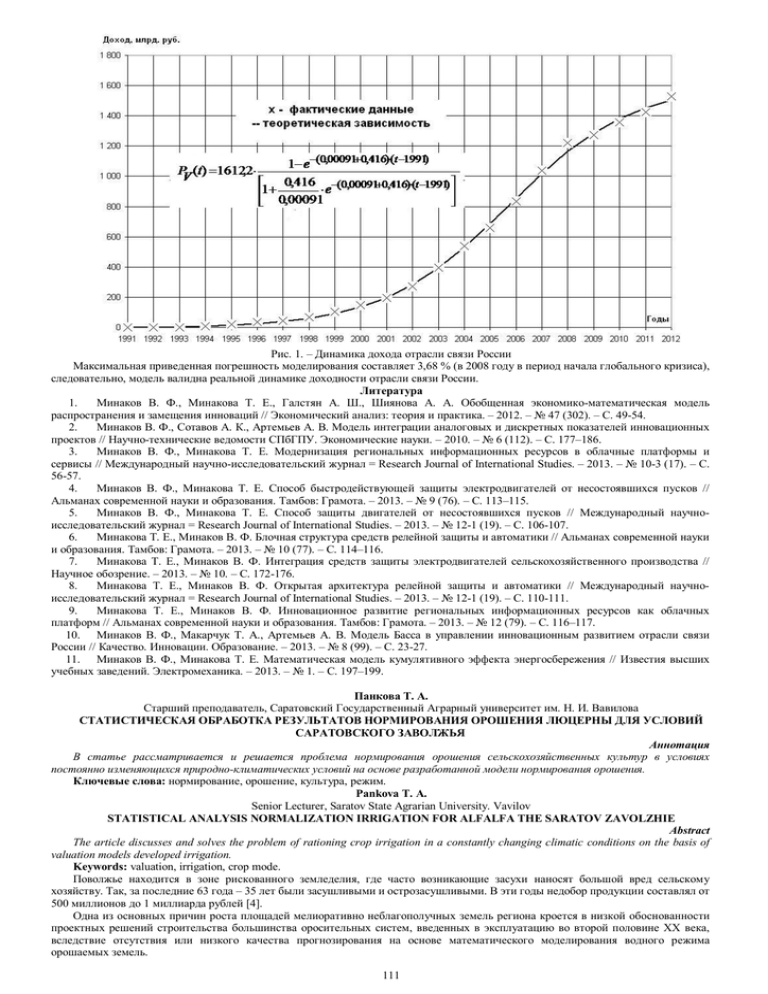
Рис. 1. – Динамика дохода отрасли связи России Максимальная приведенная погрешность моделирования составляет 3,68 % (в 2008 году в период начала глобального кризиса), следовательно, модель валидна реальной динамике доходности отрасли связи России. Литература 1. Минаков В. Ф., Минакова Т. Е., Галстян А. Ш., Шиянова А. А. Обобщенная экономико-математическая модель распространения и замещения инноваций // Экономический анализ: теория и практика. – 2012. – № 47 (302). – С. 49-54. 2. Минаков В. Ф., Сотавов А. К., Артемьев А. В. Модель интеграции аналоговых и дискретных показателей инновационных проектов // Научно-технические ведомости СПбГПУ. Экономические науки. – 2010. – № 6 (112). – С. 177–186. 3. Минаков В. Ф., Минакова Т. Е. Модернизация региональных информационных ресурсов в облачные платформы и сервисы // Международный научно-исследовательский журнал = Research Journal of International Studies. – 2013. – № 10-3 (17). – С. 56-57. 4. Минаков В. Ф., Минакова Т. Е. Способ быстродействующей защиты электродвигателей от несостоявшихся пусков // Альманах современной науки и образования. Тамбов: Грамота. – 2013. – № 9 (76). – С. 113–115. 5. Минаков В. Ф., Минакова Т. Е. Способ защиты двигателей от несостоявшихся пусков // Международный научноисследовательский журнал = Research Journal of International Studies. – 2013. – № 12-1 (19). – С. 106-107. 6. Минакова Т. Е., Минаков В. Ф. Блочная структура средств релейной защиты и автоматики // Альманах современной науки и образования. Тамбов: Грамота. – 2013. – № 10 (77). – С. 114–116. 7. Минакова Т. Е., Минаков В. Ф. Интеграция средств защиты электродвигателей сельскохозяйственного производства // Научное обозрение. – 2013. – № 10. – С. 172-176. 8. Минакова Т. Е., Минаков В. Ф. Открытая архитектура релейной защиты и автоматики // Международный научноисследовательский журнал = Research Journal of International Studies. – 2013. – № 12-1 (19). – С. 110-111. 9. Минакова Т. Е., Минаков В. Ф. Инновационное развитие региональных информационных ресурсов как облачных платформ // Альманах современной науки и образования. Тамбов: Грамота. – 2013. – № 12 (79). – С. 116–117. 10. Минаков В. Ф., Макарчук Т. А., Артемьев А. В. Модель Басса в управлении инновационным развитием отрасли связи России // Качество. Инновации. Образование. – 2013. – № 8 (99). – С. 23-27. 11. Минаков В. Ф., Минакова Т. Е. Математическая модель кумулятивного эффекта энергосбережения // Известия высших учебных заведений. Электромеханика. – 2013. – № 1. – С. 197–199. Панкова Т. А. Старший преподаватель, Саратовский Государственный Аграрный университет им. Н. И. Вавилова СТАТИСТИЧЕСКАЯ ОБРАБОТКА РЕЗУЛЬТАТОВ НОРМИРОВАНИЯ ОРОШЕНИЯ ЛЮЦЕРНЫ ДЛЯ УСЛОВИЙ САРАТОВСКОГО ЗАВОЛЖЬЯ Аннотация В статье рассматривается и решается проблема нормирования орошения сельскохозяйственных культур в условиях постоянно изменяющихся природно-климатических условий на основе разработанной модели нормирования орошения. Ключевые слова: нормирование, орошение, культура, режим. Pankovа T. A. Senior Lecturer, Saratov State Agrarian University. Vavilov STATISTICAL ANALYSIS NORMALIZATION IRRIGATION FOR ALFALFA THE SARATOV ZAVOLZHIE Abstract The article discusses and solves the problem of rationing crop irrigation in a constantly changing climatic conditions on the basis of valuation models developed irrigation. Keywords: valuation, irrigation, crop mode. Поволжье находится в зоне рискованного земледелия, где часто возникающие засухи наносят большой вред сельскому хозяйству. Так, за последние 63 года – 35 лет были засушливыми и острозасушливыми. В эти годы недобор продукции составлял от 500 миллионов до 1 миллиарда рублей [4]. Одна из основных причин роста площадей мелиоративно неблагополучных земель региона кроется в низкой обоснованности проектных решений строительства большинства оросительных систем, введенных в эксплуатацию во второй половине ХХ века, вследствие отсутствия или низкого качества прогнозирования на основе математического моделирования водного режима орошаемых земель. 111 Поэтому, наиболее актуальной проблемой для науки и практики являются научные разработки в области нормирования водопотребления сельскохозяйственных культур посредством прогнозирования его с помощью математических ресурсосберегающих моделей. Нами была разработана математическая ресурсосберегающая модель нормирования орошения в виде совокупности уравнений, для условий Саратовского Заволжья [4]. В формуле Н.Н. Иванова [3] испаряемость (мм/мес) определяется по испарению с водной поверхности малых водоемов или с поверхности почвы при полном ее насыщении водой и связывается с метеорологическими характеристиками, температурой (Т) и относительной влажностью воздуха (а). E0 0.001825 T 100 a 2 где Т - среднесуточная температура воздуха, 0С; а - среднесуточная относительная влажность воздуха, %; При поддержании в расчетном слое почвы влажности используем выражение: Wh Whн Whк / 2 WНВ W W / 2 1 hн hк член Таким образом, расчет водопотребления с сельскохозяйственного поля проводим по формуле: , E E0 При условии Wh < Wнв определяющее значение при формировании водопотреблении сельскохозяйственных культур будет иметь влажность почвы, при Wh Wнв водопотребление определяется напряженностью метеорологических условий. Разработанная методика позволяет принимать технологическое решение для нормирования водопотребления культур при меняющихся природных условиях, путем проведения симуляции различных сценариев изменения водного режима почвы, что наиболее актуально в связи с происходящими природно-климатическими изменениями [1, 2]. Модель была разработана на алгоритмическом языке Visual Basic for Application в среде MS Excel. Алгоритм программы заключается в посуточном определении всех показателей водного режима [5, 6], и как конечный результат моделирования - определение составляющих необходимых для ресурсосберегающего режима орошения за весь вегетационный период (оросительная норма, поливная норма, сроки полива, количество поливов, водопотребление). Для определения эмпирической зависимости, которым подчиняются исследуемые параметры: средняя влажность в % от наименьшей влагоемкости и суммарное водопотребление был построен график зависимости (рис. 1) этих параметров, полученных в результате симуляции режима орошения люцерны. Рис. 1. Зависимость суммарного водопотребление люцерны (в мм) от средней за вегетационный период влажности (в % от НВ). С помощью линии тренда была получена регрессионная зависимость между средней влажностью почвы и величиной суммарного водопотребления культуры. Полученная зависимость описывается уравнением аппроксимирующей (сглаживающей) кривой, полиномом 2 степени: Е = - 0,434Wср2 + 85,64Wср - 3565 Величина достоверности аппроксимации получилась R2 = 0,842, это говорит о значимой корреляционной зависимости между суммарным водопотреблением и влажностью почвы. Литература 1. Васильченко Т. А. / Количественная оценка риска возделывания яровой пшеницы в Саратовской области. Вестник СГАУ. / Саратов, 2009. - №1. С. 12-16. 2. Васильченко Т. А., Затинацкий С. В. / Обоснование необходимости комплексных мелиораций с учетом возможного изменения климата в условиях Нижнего Поволжья. Вестник СГАУ. / Саратов, 2008. - № 3. С. 60-62. 3. Иванов, Н. Н. Об определении величин испаряемости / Н. Н. Иванов. – М.: Изв. ГГО, 1954. – С. 189 – 196. 4. Кошкин Н. М., Затинацкий С. В., Васильченко Т. А. / Автоматизация управления режимом полива сельскохозяйственных культур с учетом погодных условий. Вестник СГАУ. / Саратов, 2010. - №7. С. 58-61. 5. Панкова Т. А., Затинацкий С. В. / Ресурсосберегающая математическая модель нормирования орошения. Журнал «Научное обозрение». / Саратов, 2013. - № 11, С.10-13. 6. Панкова Т. А., Затинацкий С. В. / Моделирование режима орошения. Материалы докладов II Международной научнопрактической конференции «Фундаментальные и прикладные науки сегодня». / Москва, 2013., С.115-118. 112