определение предельной эффективной скорости и степени

УДК 550.834
А. А. МАЛОВИЧКО
ОПРЕДЕЛЕНИЕ ПРЕДЕЛЬНОЙ ЭФФЕКТИВНОЙ
СКОРОСТИ И СТЕПЕНИ СКОРОСТНОЙ
НЕОДНОРОДНОСТИ ПО ОДИНОЧНОМУ
ГОДОГРАФУ ОТРАЖЕННЫХ ВОЛН
В СЛУЧАЕ ВЕРТИКАЛЬНО-НЕОДНОРОДНОЙ СРЕДЫ
Используемые в сейсморазведке способы интерпретации годо­
графов отраженных волн в случае вертикально-неоднородных
сред с горизонтальными отражающими границами обычно
предполагают аппроксимацию наблюденного годографа t(x)
гиперболой
t = —
У 4ЯЭ2Ф + ** ,
(1)
где уЭф и Н;,ф — соответственно эффективная скорость и эф­
фективная глубина залегания отражающей границы.
Получаемые в результате аппроксимации
(1) значения
эффективной скорости, как показано в [7, 10], зависят не толь­
ко от параметров среды, но и от протяженности годографа,
•а также от способа вычисления.
2*
35
Если вычисления будем производить способом квадратич­
ных координат t2(x2), то в частном случае малого элемента
годографа для иЭф получим следующую формулу [7, 10]:
Для неоднородной среды, в которой скорость изменяется с
глубиной по закону v(z), эффективная скорость, определяе­
мая по формуле (2), сложным образом зависит от х и пара­
метров среды. Однако при х->0 она стремится к своему пре­
дельному значению
)dzdz ,
ve = lim уэф•М=
(х) = ]/.И(г)^
\/ \v{z)dz \/jV'(
\ v~l 2(г)
(3)
Х-+0
где Н — глубина залегания отражающей границы.
Вычисление этого предельного значения непосредственно
по годографу отраженных волн представляет особый интерес,
поскольку в этом случае появляется возможность пересчета
эффективных скоростей в пластовые по формуле Урупова —
Дикса [10].
В настоящее • время известно несколько способов вычисле­
ния ve по одиночному годографу отраженных волн. Наиболь­
шее распространение получил способ, основанный на аппрок­
симации по методу наименьших квадратов наблюденного го­
дографа полиномом заданной степени [1, 9]
t = a1 + a.2x* + a3xi+
. . . + апх2п'2
(4)
или [3, 11, 12]
^ = c1 + c2x2 + c 3 x 4 + . . . + спх2п~2.
(5)
При этом величина предельной эффективной скорости оп­
ределяется как
° « = уаЬг
(6)
или
Поскольку для окончательного вычисления ve надо знать
лишь свободный член (а^) и коэффициент при х2 (а2 или с2),
то нередко годограф аппроксимируют несколькими первыми
(двумя или тремя) членами полинома.
Г. Д. Кочерина [4] для нахождения предельной эффектив­
ной скорости предлагает использовать перебор гипербол
типа (1) с различными параметрами уаф. При этом ve опре­
деляется как параметр той гиперболы, которая минимально.
36
отклоняется (в среднеквадратическом смысле) от наблюден­
ного годографа t(x) в интервале расстояний х<—Нэф.
М. Аль-Чалаби [11] для вычисления ve предлагает произ­
водить многократное определение уЭф по разным частям од­
ного и того же годографа и найденные значения относить к
некоторому эффективному удалению, получаемому по формуле
' ,
т
у/2
^ = 1 — 2*4
•
<8>
где Xi — удаление i-й точки от пункта взрыва; т — число ис­
пользованных точек годографа.
График зависимости УЭФ от х%ф носит почти линейный ха­
рактер. Осреднение его по методу наименьших квадратов, а
затем экстраполяция в сторону меньших значений дают при
д;Эф = 0 значение ve.
ТЕОРЕТИЧЕСКОЕ ОБОСНОВАНИЕ СПОСОБА
В работе [5] было показано, что в вертикально-неоднородных
средах с горизонтальными отражающими границами уравне­
ние годографа отраженных волн может быть записано в виде
где
/„ = 2 J у"1 (г) dz
о
— двойное время пробега волны до отражающей границы по
вертикальному лучу; S — степень скоростной неоднородности
среды, которая определяется следующим отношением:
S = v)lv\,
(Ю)
где
•/-V1T
v3(z)dz
(11)
о
— предельная среднебиквадратическая скорость.
В случае однородной среды S = l и уравнение (9) перехо­
дит в классическое уравнение годографа
s ++ 4 .
<=l/'o
/'
v
02)
37
Для получения оптимального решения обратной кинемати­
ческой задачи воспользуемся методом наименьших квадратов,
который позволяет не только найти решение, но и оценить
его ошибку. С этой целью будем аппроксимировать наблюден­
ный годограф теоретическим, рассчитанным по формуле (9).
Для метода наименьших квадратов условие наилучшей ап­
проксимации записывается в виде
\}(t{-Tt)* = mm,
(13)
где ti — наблюденное значение годографа в точке xt; Г, — зна­
чение, рассчитанное в той же точке по формуле (9).
Поскольку Т является функцией параметров t0, ve и S, то
условие минимума выражения (13) приводит к системе трех
уравнений:
Ъ«.-ъ№)-°.
04)
. dt,
и
£
(tc-Tdf—) =0,
(15)
2j
T
0
«<~
Hi^)=
>
*
" V dS
об)
1=1
1=1
V
/дТ \ /дТ \
/дТ\
\дГ ) •' \д~ )• И ( 7^").— частные производные Т по парамет­
рам в точке Xi.
Для решения системы (14) — (16) применим следующий
прием. Предварительно зададимся приближенными значения­
ми искомых параметров v°, t° и S°, а затем разложим функ­
цию T(t0, ve, S, х) в ряд Тейлора в окрестности точки Т {t°0y
v°, S°, х) и ограничимся только линейной частью. Тогда
ГДе
r(/„»„slI)=T((U,,s,<)+(i,-e№ +
+ <°--eff) + <s-^(-s-)-
' <17>
Здесь и в последующих выкладках предполагается, что
производные рассчитываются при значениях параметров t%,
t°
v ° и S°.
Обозначив
8ve =•• ve — v°,
38
65 = S — 5°
л подставив (17) и (18)
уравнений
в
(14) — (16),
получим
(18)
систему
£(f)>-S(1=1
1=1
i=i
i=i
1=1
1=1
1=1
i=i
i=i
1=1
Решая ее, находим поправки (18) к приближенно задан­
ным значениям параметров. Повторив операцию уточнения не­
сколько раз (используй несколько итераций), можно получить
значения t0, vc и 5 с высокой точностью.
На основании изложенного выше можно наметить последо­
вательность определения предельного значения эффективной
скорости.
1. По наблюденному годографу t(x) вычисляем иЭф и t0 Эф,
которые представляют собой широко используемые на прак­
тике эффективные параметры соответствующей однородной
среды. Для этого годограф аппроксимируем гиперболой (12),
определив параметры по способу квадратичных координат
[7, 10]:
пМ-{Щ2
.2
"»*
=
0 2
2
2
•
( 22 )
I I
о
4ф =
Ъх\ Щ -
—
S*? 2*2/2
— — .
(23)
39
2. Принимаем и°=иэф, t°=t0^
и S ° = l и для каждого уда­
ления х{ рассчитываем значения производных
-W 1 -—
Г
(24)
l
-)=
—^-.
l
(S°)
(25)
-l
0
I 35 Л
) + — -•
s
w+
*°'
an/Mn
2So( u O) 2 P t
•
(26)
где
'<-]/((!)' •^w-
<27)
#
3. Вычисляем необходимые суммы, решаем систему (19) и
(21) и находим искомые поправки
д*
д„
дс
«в = ^ ,
бУе=^иб5 = ^ ,
(28)
где Д, At, Av и As — определители, составленные из коэффи­
циентов при неизвестных и свободных членах.
4. Принимаем tl0-=t°0+&t0, v\=v°e+bve, S1 = S° + 6S и повто­
ряем этапы 2 и 3.
ПРАКТИЧЕСКОЕ ОПРОБОВАНИЕ СПОСОБА
НА ТЕОРЕТИЧЕСКИХ ГОДОГРАФАХ
Результаты определения предельной эффективной скорости и
степени скоростной неоднородности по способу, основанному
на использовании формул (22) — (28), проведенные на боль­
шом количестве разнообразных моделей, позволили сделать
следующие выводы.
1. При определении v,, и S по теоретическим годографам
необходимая точность результатов всегда достигается уже
после первой итерации.
2. В случае определения ve и S по теоретическим годогра­
фам, осложненным случайными ошибками, получаемое реше­
ние не всегда устойчиво. Изучение условий устойчивости ре­
шения— довольно сложная задача, которая может быть пред­
метом специальных исследований. Эта задача в некоторой
степени аналогична изучению возможностей определения по
годографу дополнительных параметров среды [7, 8].
Сравнительную оценку возможностей и достоинств способа
проиллюстрируем расчетами на примере двухслойной модели
среды с параметрами
40
hx = 0,5 Км, vx = 2,5 км/с;
h2 = 0,5 км, v2 = 6 км/с.
Для определения »е и S использовался годограф волны,
отраженной от подошвы второго слоя. Столь резкая диффе­
ренциация скоростей и малая глубина залегания отражающей
границы (Н—\ км) позволяют выявить характерные особен­
ности различных способов.
J х,км
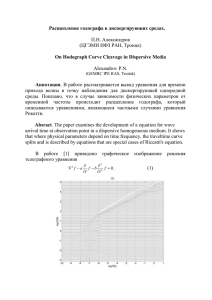
Рис. 1.
Кривые
предельной эффективной
скорости,
вычисленной по годографам
различной
длины
J
х,км
Рис. 2. Кривые предельной
эф­
фективной
скорости,
вычислен­
ной по годографу длиной 1 км
На рис. 1 приведены результаты вычисления предельной
эффективной скорости. Для расчета использовались интерва­
лы годографа различной длины. Левый конец интервала всег­
да совпадал с началом годографа .v„ = 0, а правый —с его
концом хк=\, 2,..., 7 км. Полученное значение ve относилось к
Центру интервала, т.е. к х = хи/2.
Кривые 1—3 характеризуют результаты определения ve по
способу, основанному на аппроксимации годографа отражен­
ных волн полиномом (5). По сравнению с полиномом (4) при
одинаковом количестве членов он дает лучшее приближение
годографа [5], а следовательно, обеспечивает и более высокую
точность определения ve. Кривая 1 соответствует аппроксима­
ции годографа гиперболой (двумя членами полинома), т.е.
определению ve по формуле (22), кривая 2 —тремя членами
полинома и кривая 3— четырьмя. Прямая 5 на рис. 1 и 2—
ye = const = 3,873 км/с.
Анализируя кривые 1—3 можно сделать следующие вы­
воды :
1) с увеличением длины годографа 1 = хк — хп погрешность
определения ve возрастает;
2) при выбранных нами длинах годографа погрешность
41
расчета ve тем меньше, чем выше степень аппроксимирующего
полинома.
Кривая 4 на рис. 1 — результаты вычисления ие по спосо­
бу, основанному на использовании формул (22)— (28). Видно,
что полученные значения ve близки ve = const. Так, погрешно­
сти определения предельной эффективной скорости на 1—2 по­
рядка меньше, чем при использовании аппроксимации годо­
графа гиперболой. Максимальная погрешность достигает лишь
0,8% при 1 = 4 км. Интересно, что с увеличением длины годо­
графа погрешность сначала увеличивается, а затем, достигнув
максимального значения, начинает уменьшаться.
На рис. 2 приведены результаты определения ve для интер­
валов годографа фиксированной длины 1 = хк— хн=\ км, рас­
положенных как в непосредственной близости от пункта
взрыва, так и на большом удалении от него. Последнее имеет
место при работах по методу глубинного сейсмического зонди­
рования (ГСЗ). Значение скорости, как и ранее, отнесено к
центру интервала х.
На основании сопоставления кривых 1—4 рис. 2 также
можно сделать вывод о высокой точности определения ve по
предлагаемому способу.
Отметим следующую особенность способа, основанного на
аппроксимации годографа полиномом (5). Использование
большого количества членов не обязательно повышает точность
определения ие. Так, для интервала годографа от 3 до 4 км
значение ve при аппроксимации тремя членами полинома по­
лучилось с погрешностью 14%, тогда как при аппроксимации
четырьмя членами — с погрешностью 20%. Это объясняется
тем, что с увеличением количества членов сходимость полино­
ма (5) улучшается только для небольших удалений взрыв —
прибор [2, И], в то время как для значительных удалений мо­
гут наблюдаться сильные осцилляции. Вследствие этого
использование большого количества членов для определе­
ния vP при значительных удалениях взрыв—прибор неже­
лательно.
Необходимо, кроме того, отметить следующее обстоятель­
ство. Наблюденные годографы всегда содержат случайные по­
грешности, поэтому при определении значений ve появляются
дополнительные погрешности. Как показано в работе [11], раз­
брос значений ve тем больше, чем выше степень полинома.
Так, для трехчленной аппроксимации разброс будет в 10 раз
больше, чем для двухчленной. Именно поэтому в [11] не реко­
мендуется на практике использовать даже трехчленную ап­
проксимацию.
Оценим также способ получения предельной эффективной
скорости, предложенный в [И]. На рис. 3 показан график за­
висимости эффективной скорости УЯф, определенной по фор­
муле (22), от квадрата эффективного удаления хЭф, рассчитан42
j j r o по формуле (8). Видно, что линейная зависимость иЭф
м- х\ь наблюдается только при малых удалениях. При зна­
чительных удалениях график существенно отличается от
Прямой и, следовательно,
зна­
чения Це будут ВЫЧИСЛЯТЬСЯ С
.ошибками.
V'c
Способ, основанный на испольkk_
j r
-зовании формул (22) —(28), дает
возможность одновременно с пре\г
дельной эффективной
скоростью
hft
определять степень скоростной не­
однородности среды S. Максималь­
3,8
ная погрешность определения 5 не
i
г
J
Т -Г jm j К M
превышает 10%.
В заключение необходимо отме­
Рис.
3.
Зависимость
тить, что описанный способ, строго
v^x'L ), полученная" спообоснованный для горизонтальноАль-Чалаби [11]
CO6OM
-слоистой среды, можно применять
и для определения параметров среды по годографу общей глу­
бинной точки в случае негоризонтальных отражающих границ,
если их углы наклона не превышают 10°.
i
СПИСОК ЛИТЕРАТУРЫ
1. Воробьев А. И. Определение предельной эффективной скорости по годогафам глубинных отраженных волн.— Доповш АН УРСР. Сер. Б: геол.,
геофиз., хим. и биол., 1970, № 7, с. 595—598.
2. Гольдин С. В., Суворов В. Д. Представление годографа отраженной
волны рядом Тейлора.— Геология и геофизика, 1976, № 4, с. 102—111.
3. Денисов С. М. Определение сейсмических скоростей по длинным вет­
вям годографов отраженных волн.— В кн.: Геофизические исследования Се­
вера Урало-Поволжья. Пермское книжное издательство, 1974, с. 108—113.
4. Кочерина Г. Д. Способ численного определения предельного значения
эффективной скорости по годографу отраженных волн в случае горизонталь­
но-слоистой покрывающей среды.— Прикладная геофизика, вып. 77. М., Нед­
ра, 1975, с. 56—58.
5. Маловичко А. А. Новое представление годографа отраженных волн
Для горизонтально-слоистых сред.—Прикладная геофизика, вып. 91. М., Нед­
ра, 1978, с. 47—53.
6. Пилипенко В. Н. Определение эффективных параметров сейсмической
среды по годографам отраженных волн в ГСЗ.— В кн.: Геофизические ис­
следования на Украине. Киев, Наукова думка, 1969, с. 14—18.
7. Пузырев Н. Н. Эффективные параметры годографа отраженных волн
конечной длины для горизонтально-слоистой среды.— Изв. АН СССР. Сер.
Физика Земли, 1969, № 4, с. 39—50.
8. Пузырев Н. Н. Определение параметров градиентного слоя по годо­
графу отраженных волн.— Геология и геофизика, 1976, № 9, с. 102—108.
9. Суворов В. Д. Определение предельной эффективной скорости по го­
дографу отраженных волн при произвольном изменении скорости с глуби­
ной.—Геология и геофизика, 1970, № 2, с. 92—100.
10. Урупов А. К- Изучение скоростей в сейсморазведке. М., Недра,
1966.
43
11. Al-Chalabi M. An analysis of stacking, RMS, average and interval
velocities over a horizontally laered ground.— Geophysical prospecting, vol. 22
№ 3, 1974, с 458—475.
12. Taner M. Т., Kochler F. Velocity spectra — Digital computer derivation
and applications of velocity functions.— Geophysics, vol. 34, № 6, 1969,
с 859—881.