Н.П. Хариш, И.Е. Хариш Потери энергии в стволе скважины Для

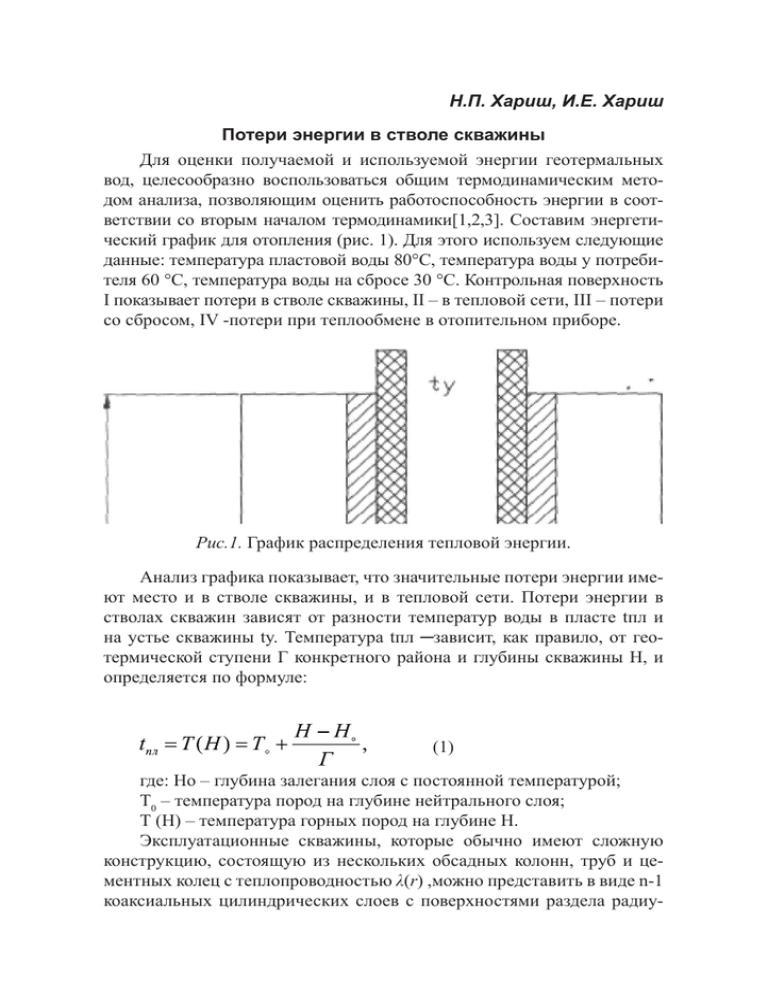
Н.П. Хариш, И.Е. Хариш
Потери энергии в стволе скважины
Для оценки получаемой и используемой энергии геотермальных
вод, целесообразно воспользоваться общим термодинамическим методом анализа, позволяющим оценить работоспособность энергии в соответствии со вторым началом термодинамики[1,2,3]. Составим энергетический график для отопления (рис. 1). Для этого используем следующие
данные: температура пластовой воды 80°С, температура воды у потребителя 60 °С, температура воды на сбросе 30 °С. Контрольная поверхность
I показывает потери в стволе скважины, II – в тепловой сети, III – потери
со сбросом, IV -потери при теплообмене в отопительном приборе.
Рис.1. График распределения тепловой энергии.
Анализ графика показывает, что значительные потери энергии имеют место и в стволе скважины, и в тепловой сети. Потери энергии в
стволах скважин зависят от разности температур воды в пласте tпл и
на устье скважины ty. Температура tпл ─зависит, как правило, от геотермической ступени Г конкретного района и глубины скважины Н, и
определяется по формуле:
(1)
где: Но – глубина залегания слоя с постоянной температурой;
Т0 – температура пород на глубине нейтрального слоя;
Т (Н) – температура горных пород на глубине Н.
Эксплуатационные скважины, которые обычно имеют сложную
конструкцию, состоящую из нескольких обсадных колонн, труб и цементных колец с теплопроводностью λ(r) ,можно представить в виде n-1
коаксиальных цилиндрических слоев с поверхностями раздела радиу-
сом r = ri.
Схематический разрез геотермальной скважины при эксплуатации
одного пласта приведен на рисунке 2.
Рис.2. Схематический разрез скважины.
При малых и средних дебитах геотермальных скважин температура
воды на устье скважины в значительной мере зависит от фактического
дебита и срока эксплуатации скважины.
Точная оценка ∆t= tпл – ty возможна в случае строгого решения сопряженной задачи нестационарного теплообмена потока геотермальной
воды в скважине с окружающим ее горным массивом.
В общем случае при учете возможности колебаний во времени
пластовой температуры tпл(τ) и дебита G(τ) поступающей в скважину
геотермальной воды необходимо учитывать изменения теплофизических параметров по глубине скважины и радиусу ее сечения г0(Н):
плотности р(Н), теплоемкости с(Н), теплопроводности λ(Н), температуропроводности а(Н) неоднородного горного массива. Математическая
формулировка задачи имеет вид:
(2)
где:
начальные условия:
Т(r,Н,τ)=Т (Н) при τ =0;
граничные условия:
(3)
T (r, Н, τ) = Т (Н) при τ = ∞;
при r = r0(Н);
здесь pG, cg – плотность и теплоемкость геотермальной воды;
а(Н,r) – коэффициент теплопередачи от воды к горным породам
через обсадную колонну скважины.
Стационарное тепловое поле зависит от расстояния от оси скважины, и искомое распределение температуры удовлетворяет уравнению:
;
(4)
граничные условия здесь:
при r = 0
;
при r = r0
при r = r1
при r = rn-1
;
при r = rn
где rn =
– условный радиус теплового влияния, на
границе которого температура горных пород предполагается невозмущенной и является известной стационарной функцией глубины.
Элементарный тепловой поток dq цилиндрической поверхности
длиной dH , согласно закону Фурье, может быть записан как
dq = 2πK(t(H) – T(Н))dН;
(5)
где К – коэффициент теплопередачи.
Теплота, теряемая водой в том же интервале dH в единицу времени,
равна: dq = GcG pG dt;
(6)
приравниваем правые части уравнений (5) и (6) находим:
(7)
Аналитические зависимости, получаемые в результате решения
уравнения (2), являются настолько сложными, что не могут быть использованы для практических расчетов.
Составление уравнения теплового баланса для потока в скважине
применительно к условиям нестационарного процесса, вместо уравнения (2) при усреднении перечисленных выше величин или для последовательного теплового расчета скважин по интервалам с существующим
изменением G, r0, с, р, λ, а, приводит к линейному дифференциальному
уравнению первого порядка
(8)
где Ка – коэффициент интенсивности теплообмена;
Кτ – коэффициент нестационарного теплообмена.
Решая линейное дифференциальное уравнение первого порядка (7)
относительно t, получаем
(9)
где tH – температура воды на глубине Н в геотермальной скважине
глубиной L.
Используя разложение по expX , пренебрегая членами выше второго порядка малости, получаем более удобную для расчета формулу:
(10)
при Н=0
(11)
Из выражения (11) следует, что при увеличении дебита геотермальной воды знаменатель дроби возрастает и возрастает числитель, так как
коэффициент теплопередачи K=f(G) увеличивается с ростом G. Однако
увеличение К с ростом G незначительно, и основную роль в снижении
температуры геотермальной воды при ее движении по стволу скважины
играет изменение дебита.
Уменьшение потерь теплоты по стволу скважины можно достичь
непрерывной эксплуатацией геотермальной скважины, увеличением
фактического дебита действующей скважины, например откачкой, либо
более совершенным вскрытием водоносного горизонта. Представляется
возможным уменьшить остывание воды по стволу скважины изолированием обсадных труб, в частности термостатированием. Этот способ
заключается в том, что скважина обсаживается двойными трубами, пространство между ними заваривается и вакуумируется .
Приведенная математическая модель позволяет исследовать тепловые процессы, происходящие в стволе скважины и разработать оптимальные режимы эксплуатации рассматриваемых скважин.
Библиографический список
1.
2.
3.
Лыков А.В. Теория теплопроводности. М.: Высшая школа, 1967. 599 с.
Лыков А.В. Тепло- и массообмен тел с окружающей средой. Минск: Наука
и техника, 1965. 183 с.
Карташов Э.М. Аналитическая теория теплопроводности и прикладной
термоупругости / Карташов Э. М., Кудинов В.А. М.: Либроком, 2012.