5. ХИМИЧЕСКИЕ РАВНОВЕСИЯ
реклама

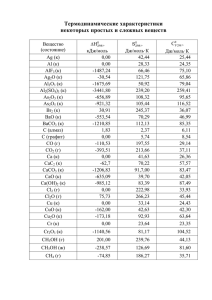
5. ХИМИЧЕСКИЕ РАВНОВЕСИЯ Равновесие имеет динамическую природу. В состоянии равновесия с равными скоростями происходит переход реагентов в продукты и продуктов в реагенты. Для рассмотренной в главе 2 системы H2, I2, HI (см. реакцию 2.3) в состоянии равновесия скоG H рости прямой и обратной реакции равны W = W , или k1[H2]e[I2]e= = k2[HI]2e. Последнее равенство можно представить в виде [HI]2 e k = 1 = KC , [H 2 ]e ⋅ [I 2 ]e k2 (5.1) где k1 и k2 – константы скоростей прямой и обратной реакций. Соотношение (5.1), связывающее константу равновесия с константами скоростей прямой и обратной реакций, называется уравнением Вант-Гоффа. Основными уравнениями, связывающими величину истинной термодинамической константы химического равновесия n1A1 + n2A2 + ... + niAi R m1B1 + m2B2 + ... + mjBj B B B (5.2) со значениями термодинамических функций веществ, участвующих в равновесии, являются RT·lnK(T) = – ∆rG0(T) = – ∆rH0T + T·∆rS0T , ∆rG0(T) = ∑ m j Δ f GT0 (B j ) − ∑ ni Δ f GT0 (A i ) , j (5.3) (5.4) i где ∆fG0T(X) – свободная энергия Гиббса (изобарноизотермический потенциал) образования вещества X в стандартном состоянии при данной температуре, ni и mj – стехиометрические коэффициенты реагентов и продуктов реакции. 78 Практические расчеты констант равновесия по известным значениям термодинамических функций (или решение обратных задач) проводятся в соответствии с основными термодинамическими определениями и законами (см. предисловие к разделу "Энергетика химических реакций"). В частности, зависимость величин ∆rH0 и ∆rS0 от температуры описывается следующими уравнениями: T ∆rH0T 0 = ∆rH 298 ∫ΔC + r 0 P ⋅ dT , (5.5) 298 T ∆rS0T = ∆rS0298 + Δ r CP0 ∫ T ⋅ dT . 298 (5.6) Величины ∆rH0298 , ∆rS0298 и Δ r CP0 можно рассчитать по справочным значениям ∆fH0298, S0298 и C0P(T) участников реакции (5.2), представленным в [1] – [4]. Истинная термодинамическая константа равновесия реальных газов и растворов связывает равновесные летучести (или активности) газов (или соответственно растворенных веществ), участвующих в реакции (5.2). Для многих практически важных расчетов и оценок (при не слишком высоких давлениях и не слишком низких температурах) летучести реальных газов можно считать равными их парциальным давлениям. В случае растворов активности растворенных веществ равны их концентрациям только при низких концентрациях. Особенно большие различия между активностями и концентрациями имеют место в растворах, содержащих сильные электролиты. В разбавленных растворах сильных электролитов взаимодействие между ионами представляет собой простое кулоновское притяжение или отталкивание. Учёт этого взаимодействия и вычисление коэффициента активности представлены в теории Дебая–Хюккеля. Изложение этой теории довольно подробно приведено в [18]. Было показано, что в таких растворах коэффициент активности γi иона с зарядом zi выражается формулой 79 lqγ = − A ⋅ z 2 ⋅ I , i i (5.7) 3 ⎤ 2 2πN A ⋅ mраств. 1 ⎡ e2 где А = . ⎢ ⎥ ⋅ 2,303 ⎣ 4πε 0 ⋅ ε ⋅ k ⋅ T ⎦ V Для воды при 298 К, ε = 78,54 значение А = 0,509 л0,5/моль0,5. Ионная сила I определяется соотношением I= 1 1 2 2 2 ∑ Ci zi = ( C1 z1 + C2 z2 + ") , 2 i 2 где суммирование распространяется на все виды ионов в растворе, а Сi – молярная концентрация i-го иона. Если перейти к среднему ионному коэффициенту активности, то выражение для него будет иметь вид lqγ ± = − 0,509 ⋅ z+ ⋅ z− ⋅ I . (5.8) где ⏐z+⏐ и ⏐z–⏐ – модули зарядов ионов, для которых вычисляется величина γ±. Формула (5.8) справедлива для растворов с ионной силой около 0.01 М и представляет собой предельный закон для малых концентраций, как и закон идеальных газов для низких давлений. При выводе этой формулы учтены только дальнодействующие кулоновские силы при размерах ионов, стремящихся к нулю. Для реакции (5.2), идущей в газовой фазе, в приближении идеального газа можно выразить константу равновесия через молекулярные статистические суммы её участников. Формулу (5.3) можно переписать в виде 0 Δ r H (0) R ⋅ ln K P (T ) = Δ r Φ 0(T ) − , (5.9) T 80 где Δ r Φ 0(T ) = Δ r S(0T ) − 0 Δ r H (0T ) − Δ r H (0) − изменение приведенной T энергии Гиббса в результате реакции, ∆rH00 – тепловой эффект реакции при 0 К. Верхний индекс «0» обозначает, что давления участников реакции соответствуют стандартному состоянию и равны 1 атм (101325 Па). По рекомендации ИЮПАК за стандартное состояние принято давление 1 бар (105 Па). Очень часто эту разницу в 1,3% можно считать несущественной. Приведённая энергия Гиббса выражается через молекулярную статсумму формулой Z (T ) Φ 0(T ) = R ⋅ ln , (5.10) NA Подставляя в (5.9) выражение (5.10), получим формулу для расчета константы равновесия реакции (5.2): ⎛ 1 ⎞ K P (T ) = ⎜ ⎟ ⎝ NA ⎠ Δr n ⎛ Z m1 ⋅ Z m2 ⋅ " ⋅ Z m j B1 B2 Bj ⋅ ⎜⎜ n n n ⎜ Z A11 ⋅ Z A22 ⋅ " ⋅ Z Aii ⎝ ⎞ −Δ H ⎟ RT , ⎟⋅e ⎟ ⎠ 0 r (0) (5.11) где Z Ai и Z B j – молекулярные статистические суммы веществ, участвующих в реакции, вычисленные для стандартного давления. В (5.11) размерность KР(Т) зависит от выбора стандартного Δ n состояния и соответствует (атм) r . Таким образом, для расчета химического равновесия в системе можно ограничиться расчетом S0(T) , C0Р(T) и [H0(T) – H0(0)] для каждого вещества, участвующего в реакции. Величины ∆rH0(0) определяются из справочных данных, в основе составления которых лежат экспериментальные значения тепловых эффектов реакций. 81 Примеры решения задач Задача 1. Для NH4Br(кр.) и газообразных продуктов его термического разложения (NH3 и HBr) стандартные термодинамические характеристики равны: Вещество ∆fH0298, кДж/моль S0298, Дж/(моль·К) C0P,298, Дж/(моль·К) NH4Br(кр) NH3(г) HBr(г) –270,1 –46,2 –34,1 112,8 192,6 198,6 88,7 35,6 28,0 Найти давление газа над NH4Br(кр) при 600 К, считая, что величины C0P не зависят от температуры. Решение. По данным, приведенным в таблице, находим сначала величины ∆rH0298, ∆rS0298 и ∆rC0P: ∆rH0298 = ( –46,2 – 34,1 + 270,1) = 189,8 кДж/моль, ∆rS0298 = (192,6 + 198,6 – 112,8) = 278,4 Дж/(моль·К), ∆rC0P = (35,6 + 28,0 – 88,7) = –25,1 Дж/(моль·К). Далее, используя соотношения (5.5) и (5.6) в приближении ∆rCP = const, получаем ∆rH0600 = ∆rH0298 + ∆rC0P (600 – 298) = 182,2 кДж/моль, 600 = 260,8 Дж/(моль·К). 298 Константу равновесия при 600 К находим из уравнения (5.3): ∆rS0600 = ∆rS0298 + ∆rC0P ln ln K P = − 0 Δ r H 600 Δ S0 + r 600 = −5,16 ; R 600 RT 82 КP = 5,75·10–3 атм2. Поскольку KP = PNH3 ⋅ PHBr и PNH3 = PHBr , окончательно получаем PNH3 = PHBr = K P = 0,076 атм; P = PNH3 + PHBr = 0,152 атм. Задача 2. Вычислить константу равновесия диссоциации уксусной кислоты (СН3СООН) в водном растворе при 298 К с учётом диссоциации воды. Необходимые термодинамические данные взять из справочника [1]. Решение. Реакция диссоциации уксусной кислоты в водном растворе сопряжена с диссоциацией воды и будет существенно влиять на величину концентрации ионов ОН–(р–р). Нижний индекс (р–р) в дальнейшем опустим. Для удобства вычислений суммарную реакцию можно записать в таком виде: СН3СООН R СН3СОО– + Н+, + Н+ + ОН– R Н2О(ж)______________________ СН3СООН + Н+ + ОН– R Н2О(ж) + СН3СОО– + Н+. Константа равновесия суммарной реакции КС равна ⎡⎣ H 2 O (ж) ⎤⎦ ⎡⎣ CH 3 COO − ⎤⎦ ⎡⎣ H + ⎤⎦ K (CH COOH) 3 = d KC = K d (H 2 O (ж) ) [CH3COOH ] ⎡⎣ H + ⎤⎦ ⎡⎣OH − ⎤⎦ и определяется отношением константы диссоциации уксусной кислоты Kd(СН3СООН) к константе диссоциации воды Kd(Н2О(ж)). Константу диссоциации воды можно представить так: 83 ⎡ H + ⎤ ⎡ OH − ⎤⎦ KВ K d ( H 2 O(ж) ) = ⎣ ⎦ ⎣ = , ⎡⎣ H 2 O(ж) ⎤⎦ ⎡⎣ H 2 O (ж) ⎤⎦ где KВ = [Н+][ОН–] = 1,008⋅10–14 М2 – ионное произведение воды при Т = 298 К [1], [H2O(ж)] = 1000 г/л = 55, 6 моль/л = 55, 6 M. 18 г/моль Константа равновесия KС может быть найдена из формул (5.3) и (5.4): 0 − RT ln K C = Δ r G298 , (а) 0 0 0 Δ r G298 = Δ f G298 (H 2 O (ж) ) + Δ f G298 (СH 3COO − ) − 0 0 −Δ f G298 (CH 3COOH (ж) ) − Δ f G298 (OH − ). (б) Величина ΔfG0298(H+) = 0 (см. раздел 1, с. 11). Величины ΔfG0298 (Х) можно найти в справочниках, но можно и вычислить по справочным значениям энтальпии образования и энтропии. Вычислим эти значения для воды и уксусной кислоты, а для ионов возьмём их из справочника [1]. Стандартные свободные энергии Гиббса образования ионов: ΔfG0298 (СН3СОО–) = –369,4 кДж/моль, ΔfG0298 (ОН–) = –157,35 кДж/моль. Для вычисления ΔfG0298(H2О(ж)) и ΔfG0298(СH3СООН(ж)) запишем реакции образования H2О(ж) и СH3СООН(ж) из простых веществ, величины ΔfG0298 которых равны нулю (так же, как и ΔfН0298 этих веществ): 1) Н2 + 0,5О2 = Н2О(ж) – ΔfН0298,1, 2) 2Сграфит + 2Н2 +О2 = СН3СООН(ж) – ΔfН0298,2. Согласно этим реакциям 84 ΔfG0298 (Н2О(ж)) = ΔfН0298,1 – 298 К⋅ΔfS0298,1, ΔfG0298 (СН3СООН(ж)) = ΔfН0298,2 – 298 К⋅ΔfS0298,2. Поэтому для вычислений используем справочные данные из [1] по стандартным энтальпиям образования и энтропиям участников реакций 1) и 2). Сведём их в таблицу: Вещество Н2О (ж) СН3СООН (ж) Н2 (г) О2 (г) Сграфит ∆fH0298 , кДж/моль –285,83 –484,09 0 0 0 S0298 , Дж/(моль·K) 69,95 159,83 130,52 205,04 5,74 В соответствии с реакциями 1) и 2) их энтальпии в стандартных условиях равны: ΔfН0298,1 = ∆fH0298(Н2О (ж)) = –285,83 кДж/моль, ΔfН0298,2 = ∆fH0298(СН3СООН (ж)) = –484,09 кДж/моль. Тогда ΔfG0298 (Н2Ож) = –285,83 кДж/моль –298 К·(69,95 – 130,52 – – 0,5·205,04) Дж/(моль·К) = –237,2 кДж/моль. ΔfG0298 (СН3СООНж) = –484,09 кДж/моль – 298 К·(159,83 –2·5,74 – – 2·130,52 – 205,04) Дж/(моль·К) = –389,4 кДж/моль. Подставляя значения величин в формулу (б), получим 0 Δ r G298 = −237, 2 − 369, 4 + 389, 4 + 157,35 = −59,85 кДж/моль. Из формулы (а) следует значение константы равновесия суммарной реакции 85 ⎡ Δ G0 ⎤ ⎡ −59850 ⎤ 10 K C = exp ⎢ − r 298 ⎥ = exp ⎢ − ⎥ = 3,1 ⋅ 10 . 8,31 ⋅ 298 RT ⎣ ⎦ ⎣ ⎦ Константа равновесия процесса диссоциации уксусной кислоты в водном растворе равна K d (CH 3COOH) = K C ⋅ K d (H 2 O(ж) ) = K C ⋅ = KВ = ⎡⎣ H 2 O(ж) ⎤⎦ 3,1 ⋅ 1010 ⋅ 10−14 M 2 = 3,1 ⋅ 1010 ⋅ 1,8 ⋅ 10−16 M = 0,57 ⋅ 10−5 M. 55,6 M Найденная величина константы диссоциации уксусной кислоты почти на 11 порядков превышает константу диссоциации воды, которая равна 1,8⋅10–16 М. Концентрация Н+ в растворе будет определяться диссоциацией уксусной кислоты, а концентрация ОН– существенно уменьшится в соответствии с величиной ионного произведения воды. Значение термодинамической константы диссоциации уксусной кислоты в водном растворе, выраженной через активности, приведено в [1]: Kd(СН3СООН) = 1,754⋅10–5 М для Т = 298 К. Отметим, что аналогичный термодинамический расчёт константы диссоциации уксусной кислоты в водном растворе по реакции СН3СООН R СН3СОО– + Н+ даёт завышенное значение KD(CH3COOH) = 3,1⋅10–4 М. Эти результаты следует признать вполне удовлетворительными. Более точный расчёт должен, по-видимому, учитывать теплоту растворения уксусной кислоты в водном растворе. Задача 3. Произведение растворимости BaSO4 в воде при 25 С равно 1,1·10−10 М2. Найти растворимость BaSO4 в 0,01 М водном растворе КСl. о Решение. По определению произведения растворимости можно записать 86 ПР = aBa 2+ ⋅ aSO 2− = [Ba 2+ ] ⋅ [SO 24− ] ⋅ γ ±2 4 Средний коэффициент активности γ± найдём, используя предельный закон Дебая – Хюккеля (см.(5.8)). При вычислении ионной силы раствора концентрациями Ва2+ и SO42− можно пренебречь ввиду малой растворимости ВаSO4 в воде. I = 1/2⋅( [K+]·12+ [Cl−]⋅(−1)2 ) = 0,01 M; lg γ±= −│Z+⋅Z−│·A I = −2⋅2⋅0,51 л0,5/моль0,5 0, 01M = − 0,204; γ± = 0,625. Концентрацию любого из ионов в растворе над ВаSO4(кр) находим из равенства [Ba 2+ ] = [SO 24− ] = 1,1 ⋅10−10 M = 1, 7 ⋅10−5 M , 0, 625 что, очевидно, равно растворимости этой соли. Отметим, что она выше, чем в чистой воде, где [Ba 2+ ] = [SO 24− ] = 1,1 ⋅10−10 M = 1, 05 ⋅10−5 M. 87 ЗАДАЧИ 5.1. Идеальные газы Н2 и Cl2 реагируют в адиабатических условиях при постоянном объеме. Укажите знаки ∆rH, ∆rU, ∆rS, ∆rF и механической работы A для этой реакции. Энергии разрыва связей Cl–Cl, H–H, H–Cl равны соответственно 242,6; 436; 431,6 кДж/моль. 5.2. Цинк реагирует с разбавленной серной кислотой с выделением тепла в открытом сосуде. Укажите знаки ∆rH, ∆rU, ∆rS, ∆rG и механической работы A для этой реакции. 5.3. Если тепловой эффект реакции в газовой фазе при 300 К АВ2 R А + В2 (А, В – атомы) равен нулю, то величина KP при 300 К: а) равна 1; б) равна 0; в) 0 < KP < 1; г) KP > 1. Выбор обосновать. 5.4. При 298 К газовое равновесие СО2 + Н2 R СО + Н2О характеризуется величинами K = 10−5, ΔrS0298 = 42,0 Дж/(моль·К). Рассчитайте равновесный состав для эквимолярной смеси СО и Н2О при 1000 К и Р = 10 атм. 5.5. Степень диссоциации Cl2 при Р = 1 атм, Т = 1000 и 1500 К равна 1,9·10–4 и 2,0·10–2 соответственно. Оцените энергию связи Cl–Cl. 5.6. В результате установления равновесия А + В R 2С при (РА)0 = (РВ)0 = 2,5 атм равновесные давления вещества С равны (РС)e = 1 мм рт.ст. при 1000 К и (РС)e = 20 мм рт.ст. при 1500 К. Чему равна величина ∆rS0? 88 5.7. Газовое равновесие А+В R С+D при температуре 298 К характеризуют величины K = 10–2 и ∆rS0298 = 46 Дж/(моль·К). Какое количество тепла надо подводить к реактору непрерывного действия для поддержания изотермического режима работы (Т = 700 К), если в реактор ежечасно поступает по 100 молей веществ А и В, а из реактора выходит равновесная смесь веществ А, В, С и D? 5.8. Для равновесия 2NO2 R N2O4 при 298 К KР = 15 атм–1, а ∆rH0250–400 = –58,5 кДж/моль. Какое количество тепла надо отвести от сосуда объемом 1 л, заполненного NO2 при 350 К, для того, чтобы установление равновесия прошло при постоянной температуре? Начальное давление NO2 в сосуде 2 атм. 5.9. Оцените, при какой температуре давление хлора над FeCl3 (тв), образующегося в результате установления равновесия 2FeСl3 (тв) R 2FeCl2 (тв) + Сl2 (г) , достигает одной атмосферы. Энтальпии образования и энтропии реагентов представлены в таблице: Вещество FeCl3 (тв) FeCl2 (тв) Cl2 (г) ∆fH0298 , кДж/моль –399,4 –341,7 0 S0298 , Дж/(моль·К) 145 118 223 5.10. В таблице приведены уравнения реакций и константы равновесия KС для ряда процессов. Определить значения ∆rF0T для 89 этих равновесий при заданных температурах, считая газы и растворы идеальными. Равновесие № 1 2 3 4 5 6 7 8 2С2H6 (г) R C3H8 (г) + Н2 (г) Т, К 700 KС 4,0 С2H5ОН(г) R CH3СНО(г) + Н2(г) 500 НСООСН3 (г) + 2Н2 (г) R 2CH3ОН(г) 500 3СО(г) + 2Н2О(г) R CH3ОН(г) + 2СО2(г) 1000 NH4Сl(тв) R NH3 (г) + НCl(г) 610 2FeSO4 (тв) R Fe2O3 (тв) + SO3 (г) +SO2 (г) 900 HCOOH R H+ + HCOO– (вод. р-р) 300 2+ 2– BaCO3 (тв) R Ва + CO3 (вод. р-р) 300 1,1·10–3 М 4,1·104 М–1 4,1·10–4 М–2 1,0·10–4 М2 7,0·10–6 М2 1,8·10–4 М 8,0·10–9 М2 5.11. Пользуясь приведенными термодинамическими характеристиками, вывести уравнение температурной зависимости константы равновесия С(тв) + Н2О(г) R СО(г) + Н2 (г) вида lgKP = f(T). Вещество С(тв) Н2О(г) СО(г) Н2 (г) ∆fH0298, кДж/моль 0 –241,8 –110,5 0 S0298, Дж/(моль·К) 5,7 188,7 197,5 130,5 C0P,298, Дж/(моль·К) 8,5 33,6 29,1 28,8 5.12. На основании приведенных стандартных термодинамических характеристик веществ, приведенных в таблице: Вещество Этан, С2Н6 Этилен, С2Н4 Водород, Н2 ∆fH0298, кДж/моль –84,7 52,3 0 S0298, Дж/(моль·К) 229,5 219,4 130,5 90 C0P,298, Дж/(моль·К) 52,7 43,6 28,8 вывести уравнение температурной зависимости константы равновесия вида lgKP = f(T) для газовой реакции С2Н6 R С2Н4 + Н2. 5.13. Найти состав равновесной смеси в процессе изомеризации нормального пентана при Т = 800 К и Р = 10 атм: н-С5Н12 R изо-С5Н12, н-С5Н12 R С(СН3)4, если величины ∆fG0800 для н-пентана, изо-пентана и тетраметилметана соответственно равны –43,05; –49,09 и –50,33 кДж/моль. 5.14. При Т = 100 К и Р = 1 атм равновесная степень диссоциации N2O по уравнению 2 N2O R 2NO + N2 равна 0,666. Пользуясь значением ∆fH0298 (NO) = 90,3 кДж/моль и величинами энтропий и теплоемкостей для N2O, NO, N2 , рассчитайте величину ∆fH0298(N2O). Вещество N2O NO N2 S0298, Дж/(моль·К) 219,9 210,6 191,5 C0P,298, Дж/(моль·К) 38,6 29,9 29,1 5.15. Известны уравнения температурной зависимости констант равновесий 5770 lgKP = − 2,67 − 1,70 ⋅ lg T , 2 NO + O2 R 2 NO2, T 9444 + 0,85 N2 + O2 R 2 NO, lgKP = T и величины S0298(N2) = 199,9 и S0298(О2) = 205,0 Дж/(моль·К). Рассчитайте величины ∆fH0298 и S0298 для NO и NO2. 91 5.16. Температурная зависимость константы равновесия для реакции Н2О(г) + СО R Н2 + СО2 приближенно описывается уравнением lgK = 2156 0 − 2, 2 , а ∆rH 298 T сгорания СО составляет –283,0 кДж/моль. Рассчитайте стандартную энтальпию образования Н2О(г). 5.17. При нагревании паров HBr в условиях постоянного объR H2 + Br2 происходит ема наряду с реакцией 2НBr диссоциация Br2 R 2Br. При 600 °С равновесные концентрации [Н2]e и [Br]e равны 0,2 М и 5.10–3 М, а при 800 °С равны 0,5 М и 0,1 М соответственно. Рассчитайте величину энергии диссоциации Br2 в этом диапазоне температур. 5.18. При 298 К реакция Н2 (г) + I2 (г) R 2HI(г) характеризуется константой равновесия K1 = 6,5·102, а давление I2(г) над I2(кр) в равновесии составляет 0,31 Торр. Стандартная энтальпия ∆fH0298(HI(г)) = 26,6 кДж/моль. Определить KР для гетерогенного равновесия Н2(г) + I2(кр) R 2HI(г) при 400 К, считая величины ∆fН0 для всех соединений не зависящими от температуры. 5.19. При сгорании 1 моля CCl4 до СО2 и Cl2 выделяется 254,2 кДж/моль. Степень диссоциации СО2 до СО и 1/2 О2 при 1000 К и давлении PCO2 = 10–2 атм равна 7·10–7, а при 2000 К и том же давлении – 7·10–2. Определите тепловой эффект реакции CCl4 + 0,5O2 R CO + 2Cl2. 92 5.20. Константа гетерогенного равновесия А(г) + В(тв) R С(г) + Д(г) характеризуется следующей температурой зависимостью: 5000 lgKP = − 7, 0 . T Определите общее давление в системе при 715 К и постоянном объеме V = 2 л, если в исходной смеси [A]0 = 10–2 М, [C]0 = [Д]0 = = 3·10–2 М. Какова величина максимальной работы рассматриваемой реакции? 5.21. Для слабой одноосновной кислоты константа равновесия K = 10−7 М. Концентрация кислоты в водном растворе С = 10−3 М. Рассчитайте рН и ионную силу раствора. 5.22. Сосуд постоянного объема заполнен молекулярным хлором при Р = 1 атм и 298 К. Измеренная при 1000 К концентрация атомарного хлора оказалась равной 5,2·1015 см–3. При 2000 К давление газа в сосуде достигает 7,6 атм. Проведите приближенный расчет S0298(Сl2), принимая ∆rСP ≈ 0. 5.23. Рассчитайте концентрацию ионов Н+ в водном растворе NaCl с концентрацией 0,01 М при 25 ºС. Ионное произведение воды при этой температуре равно 10−14 М2. 5.24. В какую сторону изменится степень диссоциации муравьиной кислоты НСООН при добавлении в раствор больших концентраций KСl? 5.25. Степень диссоциации кислоты НА в 0,01 – молярном водном растворе при 25 ºС составляет 0,09. Вычислите термодинамическую константу диссоциации кислоты, считая, что коэффициент активности недиссоциированной кислоты γНА = 1. 93 5.26. Оцените, во сколько раз изменится константа диссоциации KС слабой одноосновной кислоты при добавлении к 1 л её разбавленного раствора (10−3 М) 0,02 молей CaCl2. 5.27. Рассчитайте константу равновесия KР реакции диссоциации СО при 2000 К, если для молекулы СО известны значения rC–O = 0,113 нм; ω0 = 2170 см–1; ∆DН00 = 1072 кДж/моль. 5.28. Определить степень диссоциации молекулярного водорода при 3000 К и 1 атм, если rH–H = 0,0741 нм, ω0 = 4397 см–1. 5.29. Рассчитать константу равновесия реакции изотопного обмена D + H2 R H + DH при 298 К. Равновесные расстояния и силовые постоянные молекул H2 и DH считать одинаковыми. 5.30. Определить мольную долю атомарного йода в системе I2(г) R 2I(г), ∆rH00 = 149 кДж/моль, находящейся в равновесии при Р = 1 атм и Т = 1000 К. Для молекулы йода rI–I = 0,267 нм; ω0 = 214,5 см–1; M I2 = 256 г/моль. Основное состояние атома йода четырежды вырождено. 5.31. Вычислить константу равновесия для реакции N2 R 2N при Т = 3000 К и Р = 1 атм. Энергия связи в молекуле азота 941,6 кДж/моль. Основное состояние атома N имеет статистический вес g0 = 4, а для N2 g0 = 1. Характеристические температуры вращательного и колебательного движения молекулы N2 равны 2,9 К и 3390 К. 94