Тема 3. Текст
реклама
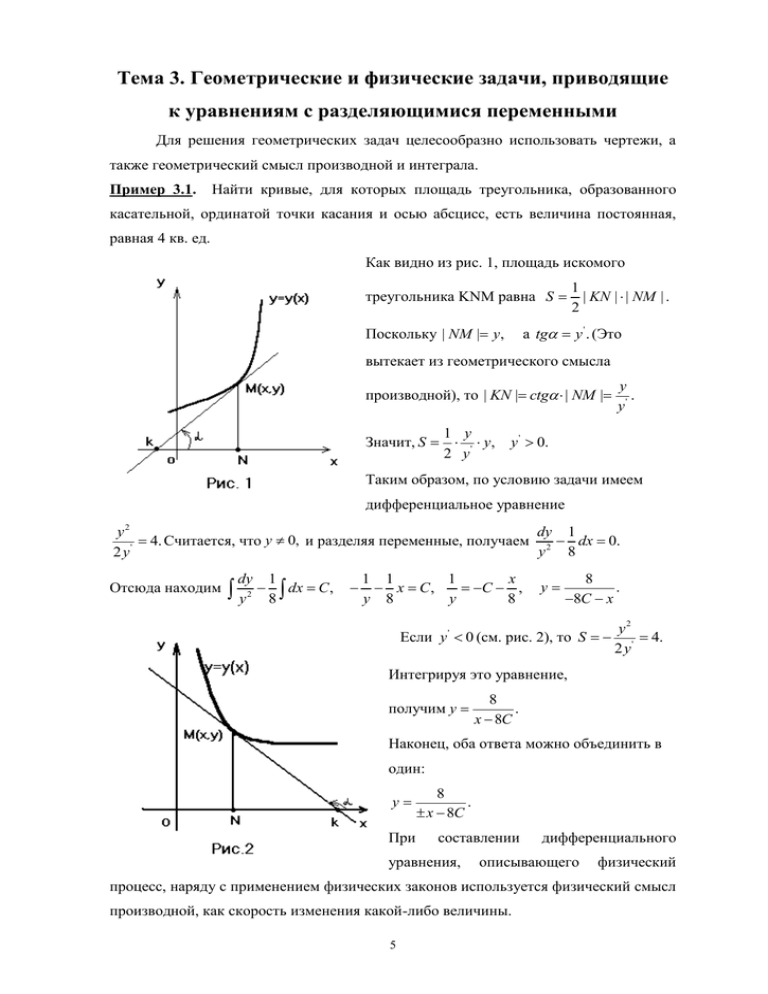
Тема 3. Геометрические и физические задачи, приводящие к уравнениям с разделяющимися переменными Для решения геометрических задач целесообразно использовать чертежи, а также геометрический смысл производной и интеграла. Пример 3.1. Найти кривые, для которых площадь треугольника, образованного касательной, ординатой точки касания и осью абсцисс, есть величина постоянная, равная 4 кв. ед. Как видно из рис. 1, площадь искомого треугольника KNM равна S 1 | KN | | NM | . 2 а tg y ' . (Это Поскольку | NM | y, вытекает из геометрического смысла производной), то | KN | ctg | NM | 1 y Значит, S ' y, 2 y y . y' y ' 0. Таким образом, по условию задачи имеем дифференциальное уравнение dy 1 y2 4. Считается, что y 0, и разделяя переменные, получаем 2 dx 0. ' y 8 2y Отсюда находим dy y 2 1 dx C , 8 1 1 1 x x C, C , y 8 y 8 y 8 . 8C x Если y ' 0 (см. рис. 2), то S y2 4. 2 y' Интегрируя это уравнение, получим y 8 . x 8C Наконец, оба ответа можно объединить в один: y При 8 . x 8C составлении уравнения, дифференциального описывающего физический процесс, наряду с применением физических законов используется физический смысл производной, как скорость изменения какой-либо величины. 5 Пример 3.2. С некоторой высоты сброшено тело, масса которого равна m. Требуется установить, по какому закону будет изменяться скорость v падения этого тела, если на него, кроме силы тяжести, действует тормозящая сила сопротивления воздуха, пропорциональная скорости (с коэффициентом пропорциональности k). dv dv F , где есть ускорение движущего dt dt Решение: По второму закону Ньютона m тела, а F – сила, действующая на тело в направлении движения. Эта сила складывается из двух: силы тяжести mg и силы сопротивления воздуха kv. Итак, m dv mg kv. Это соотношение и является дифференциальным уравнением dt относительно неизвестной функции v. Задания для самостоятельной работы 1. Найти такую кривую, проходящую через точку (0;–2), чтобы тангенс угла наклона касательной в любой точке равнялся ординате этой точки, увеличенной на три единицы. (Ответ: y e x 3 ). 2. Найти кривые, обладающие тем свойством, что отрезок касательной к кривой, заключенный между осями координат, делится в точке касания пополам. (Ответ: y c ). x 3. Найти кривые, у которых точка пересечения любой касательной с осью абсцисс имеет абсциссу, вдвое меньшую абсциссы точки касания. (Ответ: y Cx 2 ). 4. Найти кривые, обладающие следующим свойством: если через любую точку кривой провести прямые, параллельные осям координат, до встречи с этими осями, то площадь полученного прямоугольника делится касательной, проведенной к этой кривой в соотношении 1:2. (Ответ: y 2 Cx3 ). 5. По закону Ньютона скорость охлаждения какого-либо тела в воздухе пропорционально разности между температурой Т тела и температурой воздуха 0 T0 . Если температура воздуха равна 20 C , и тело в течении 10 минут 0 охлаждается от 100 до 60 C , то через сколько времени его температура 0 понизится до 25 C ? (Ответ: 40 минут). 6. Лодка замедляет свое движение под действием сопротивления воды, которое пропорционально скорости лодки. Начальная скорость лодки 1,5 м/сек, скорость 6 ее через 4 сек 1 м/сек. Когда скорость уменьшится до 1 см/сек? Какой путь может пройти лодка до остановки? (Ответ: 50 сек; 15 м). 7. Согласно опытам, в течение года из каждого грамма радия распадается 0,44 мг. Через сколько лет распадется половина имеющегося количества радия? (Ответ: 1600 лет.) 8. В баке находится 100 л раствора, содержащего 10 кг соли. В бак непрерывно подается вода (5 л в минуту), которая перемешивается с имеющимся раствором. Смесь вытекает с той же скоростью. Сколько останется соли в баке через час? (Ответ: 0, 5 кг.) 9. Парашютист прыгнул с высоты 1,5 км, а раскрыл парашют на высоте 0,5 км. Сколько времени он падал до раскрытия парашюта? Известно, что предельная скорость падения человека в воздухе нормальной плотности составляет 50 м/c. Изменением плотности пренебречь. Сопротивление пропорционально квадрату скорости. (ответ: 23 сек.) 7




