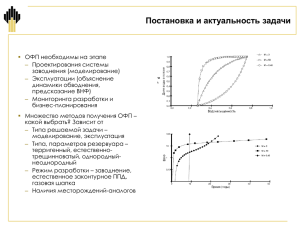
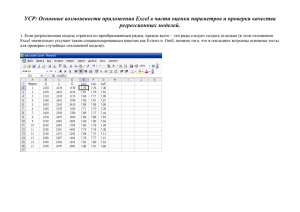
Эффекты анизотропии при циклическом взаимном вытеснении

УДК 681.3:622.24
Ю.С. Антоневич
Институт проблем нефти и газа РАН
ЭФФЕКТЫ АНИЗОТРОПИИ ПРИ ЦИКЛИЧЕСКОМ ВЗАИМНОМ
ВЫТЕСНЕНИИ ГАЗА ВОДОЙ
Структура насыщенного пласта сама по себе довольно сложна, реальные пористые и трещиноватые среды, коллекторы углеводородного сырья, как правило, проявляют анизотропию – «неодинаковость» физических свойств в различных направлениях.
Кроме того, часто включает в себя области порового пространства, заполненные не одной, а несколькими различными фазами. В частности, при создании и эксплуатации
подземных хранилищ газа в водоносных пластах. Поэтому задачи многофазной фильтрации в анизотропных пористых средах представляют большой практический интерес.
В работе будем рассматривать задачи взаимного вытеснения газа водой в ортотропном пористом пространстве. При этом вытеснение будет носить циклический характер. Каждый цикл состоит из закачки в пласт определенного объема газа и последующего его отбора, что соответствует циклическому характеру работы ПХГ. Основная задача о циклической работе подземного хранилища газа состоит в том, чтобы
определить, как влияют анизотропные свойства породы на процесс фильтрации, выяснить, как меняются от цикла к циклу размеры хранилища, отношение объемов закачиваемого и отбираемого из пласта газа и как растет объем так называемого защемленного газа. В частности, важен вопрос, выходит ли газохранилище на предельный режим,
т.е. режим, при котором размеры хранилища не увеличиваются, а объем извлекаемого
газа практически равен объему закачиваемого [1,2].
В задачах многофазной фильтрации в анизотропной пористой среде для каждой
из фаз считается справедливым обобщенный закон Дарси, т.е. постулируется линейная
G
связь между полем скоростей w и полем градиентов фильтрационного давления ∇p [1,
3]. При фильтрации ньютоновской вязкой жидкости геометрические и физические
свойства можно разделить и представить линейную связь соотношением:
k ij
w =−
∇jp
μ
i
или
∇ j p = − μ rij w i ,
где μ – динамический коэффициент вязкости жидкости, а kij и rij называются тензорами
коэффициентов проницаемости и фильтрационного сопротивления соответственно, зависят только от геометрии пустотного пространства среды. Анизотропия свойств пористой среды определяется самим видом тензора kij (или rij) [3].
Таким образом, для каждой фазы закон движения задается соотношением:
α
wi = −
k ijα
μα
∇ j pα ,
где α – индекс, обозначающий номер фазы, а kijα – тензор коэффициентов фазовых проницаемостей.
С другой стороны, согласно постулату о наличии связи между тензорами коэффициентов фазовых и абсолютных проницаемостей [4], имеем:
α
k ijα = f ijkl
k kl
α
где fijkl
– компоненты тензора четвертого ранга, симметричного по первой и второй паα
– функции насыщенности s, задают
ре индексов и их перестановке. Компоненты fijkl
тензоры коэффициентов относительных фазовых проницаемостей.
Рассматривая случай ортотропной пористой среды, можно в явном виде на основе предположения о тензорном характере коэффициентов ОФП выписать общее представление функций относительных фазовых проницаемостей [5]. При таком представлении ОФП являются функциям не только локальной насыщенности, но и параметров
анизотропии, представленных в виде отношений главных значений тензора коэффициентов абсолютной проницаемости.
Была построена математическая модель задачи взаимного циклического вытеснения газа водой, учитывающая анизотропию как абсолютных проницаемостей, так и
функций ОФП. При помощи IMPES-метода построена схема ее численного решения,
которая была программно реализована для различных наборов фильтрационных параметров.
Литература
1. Максимов В.М. Основы гидротермодинамики пластовых систем. – Москва: Недра,
1994. – 201 с.
2. Басниев К.С., Кочина И.Н., Максимов В.М. Подземная гидромеханика. – Москва:
Недра, 1993. – 416 с.
3. Дмитриев Н.М. Модели анизотропных сред: учебное пособие, часть I. – Москва:
РГУ нефти и газа, 1999. – 64 с.
4. Максимов В.М., Дмитриев Н.М. Методы нелинейных тензорных функций в моделях
двухфазной фильтрации в анизотропных средах // В сб. Проблемы современной механики. – М.: Изд-во МГУ, 1998. С. 76-83.
5. Дмитриев М.Н., Дмитриев Н.М., Максимов В.М. К представлению функций относительных фазовых проницаемостей для анизотропных пористых сред // Изв. РАН.
МЖГ. 2005. № 3. С. 118–125.