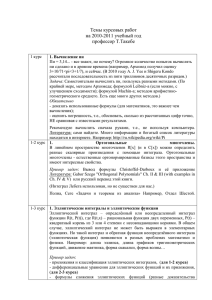
z=Найти: (3/2) z=ln(x2+y2) Найти :: (0) z=Найти: :: (1/12) Z=ex/y

z=√𝑥 3 − 𝑦 2 Найти
z=ln(x2+y2) Найти
3
2 + 𝑦Найти:
z=√𝑥
Z=ex/y Найти
z=
𝑥
Найти:
(((−
:: (1/12)
𝜕𝑦
: : (½)
∂2 z
𝜕𝑥𝑑𝑦
(((−
: : (0)
: (-1)
z=4x3y2 -5x4+2y +3. Найти
z=x2 -2y2+3xy2 -1. Найти
𝜕2𝑧
𝜕х𝜕у
𝜕2𝑧
𝜕х2
𝜕2𝑧
Z=x2-2y3+3xy2-1 . Найти
𝜕у2
(( 24х2))
((2))
((6x-12y))
Вероятность поражения цели первым стрелком равна 0,8, а для второго
стрелка равна 0,9. Какова вероятность того, что при залпе оба попадут
в цель? (((0,72)))
Вероятность появления каждого из трех независимых событий
A1,A2,A3 соответственно равны P1,P2,P3 найти вероятность
появления только первого события: (P1,q2,q3)
пи
;𝑠𝑖𝑛𝑥
Вычислить двойной интеграл ∬–2пиң;0 𝑑𝑥𝑑𝑦 (((0)))
2
3 ;𝑥3
Вычислить двойной интеграл ∬−3ң;𝑥 𝑑𝑥𝑑𝑦 (((0)))
пи
;𝑐𝑜𝑠𝑥
Вычислить двойной интеграл ∬02ң;0
𝑒2 ;
𝑑𝑥𝑑𝑦 (((1)))
1
Вычислить двойной интеграл ∬1 ң;0𝑥 𝑑𝑥𝑑𝑦 (((2)))
4 ;1/√𝑥
Вычислить двойной интеграл ∬1ң;0
𝑑𝑥𝑑𝑦 (((2)))
𝑒 ;1/𝑥
Вычислить двойной интеграл ∬1ң;0 𝑑𝑥𝑑𝑦 (((1)))
3;𝑦
Вычислить двойной интеграл ∬2 ң;0 𝑑𝑥𝑑𝑦 (((5/2)))
1
𝑥
2
𝑥
1
𝑒𝑥
Вычислить двойной интеграл ∫0 ∫0 𝑑𝑥𝑑𝑦 : (1/2)
Вычислить двойной интеграл ∫0 ∫0 𝑑𝑥𝑑𝑦 :: (2)
Вычислить двойной интеграл ∫0 ∫0 𝑑𝑥𝑑𝑦 :: (е-1)
Вычислить интеграл ∭𝐷
𝑑𝑥𝑑𝑦𝑑𝑧
(𝑥+𝑦+𝑧+1)3
, где D – область, ограниченная
координатными плоскостями и плоскостью x+y+z=1
16)))
1
𝑥2
1
𝑥
𝑦
1
𝑥
𝑦
𝑎
𝑎−𝑥
(((ln√2 − 5/
𝑦
Вычислить тройной интеграл ∫0 𝑑𝑥 ∫0 𝑑𝑦 ∫0 𝑧𝑑𝑧 (((1/42)))
Вычислить тройной интеграл ∫0 𝑑𝑥 ∫0 𝑑𝑦 ∫0 𝑑𝑧 (((1/6)))
Вычислить тройной интеграл ∫0 𝑑𝑥 ∫0 𝑑𝑦 ∫0 𝑥𝑦𝑧𝑑𝑧 (((1/48)))
𝑎−𝑥−𝑦
Вычислить тройной интеграл ∫0 𝑑𝑥 ∫0
𝑑𝑦 ∫0
𝑧𝑑𝑧 (((a4/24)))
Геометричеки каждому частному решению дифференц.уравнениия
соответствует – плоская, его график, которая называется интегральной
кривой этого уравнения
Геометрически каждому общему решению дифференц.уравнения
соответствует – совокупность(семейство) всех интегральных кривых
Два стрелка независимо друг от друга стреляют по цели. Вероятность
попадания в цель для первого стрелка равна 0,7, для второго 0,8.
Какова вероятность того, что цель будет поражена?(((0,38)))
Для функции двух переменных ∫(х, у) критическая точка М0, в
которой функция дважды дифференцируема, явл.точкой максимума,
0
0
0
0
если – 𝜟=∫𝑥𝑥 (𝑀𝑜) ∫𝑦𝑦(𝑀𝑜) − [∫𝑥𝑥(𝑀𝑜)]2 > 0 и ∫𝑥𝑥 (𝑀𝑜) <
0
0 (или ∫уу(𝑀𝑜) < 0)
Для функции двух переменных ∫(х, у) критическая точка М0, в
которой функция дважды дифференцируема, явл.точкой минимума,
0
0
0
0
если – 𝜟=∫𝑥𝑥 (𝑀𝑜) ∫𝑦𝑦(𝑀𝑜) − [∫𝑥𝑥(𝑀𝑜)]2 > 0 и ∫𝑥𝑥 (𝑀𝑜) >
0
0 (или ∫уу(𝑀𝑜) > 0)
Если ri -корни характеристического ур.линейного однородного
ур.втрого порядка y’’+a1y’+a2y=0 с постоянными коэфф.действительны
и различны, то общий интеграл уравнения выражается формулой
((у=С1er1x+C2er2x))
Если ri -корни характеристического ур.линейного однородного
ур.третьего порядка y’’’+a1y’’+a2y’+a3y=0 с постоянными
коэфф.имеет кратность 3 то общий интеграл ур. Выражается
((y=er1x(C1+C2x+C3x2)))
Если в дифференц.уравнении неизвестная функция зависит от
нескольких аргументов, то дифференц.уравнение называется
((уравнением с частными производными))
Если в дифференц.уравнении неизвестная функция зависит только от
одного аргумента, то дифференц.уравнение называется
((обыкновенным дифференциальным уравнением))
Если для функции двух переменных ∫(х, у) в точке М0 величина
0
0
0
𝜟=∫𝑥𝑥 (𝑀𝑜) ∫𝑦𝑦 (𝑀𝑜) − [∫𝑥𝑥 (𝑀𝑜)]2 < 0 то это означает
(( в точке М0 нет экстремума ))
Если поверхность задана уравнением F(x,y,z)=0 и точка M0(x0,y0,z0)
лежит на ней, то касательная плоскость к поверхности в точке М0
определяется уравнением – (x-x0)F’x(M0)+(y-y0)F’y(M0)+(zz0)F’z(M0)=0
Если поверхность задана уравнением F(x,y,z)=0 и точка M0(x0,y0,z0)
лежит на ней, то нормаль к поверхности в точке М0 опред.уравнением
𝑥−𝑥𝑜
𝑦−𝑦𝑜
𝑧−𝑧𝑜
– ′
= ′
= ′
𝐹 𝑥(𝑀𝑜)
𝐹 𝑦(𝑀𝑜)
𝐹 𝑧(𝑀𝑜)
Если у есть неявная функция одной переменной ч, заданная
∫ ′𝑥
уравнением у=∫(х, у) = 0 то производная у есть (у’= –
)
∫ ′𝑦
Если характеристическое ур.линейного однородного ур. С
постоянными коэфф.имеет пару однократных комплексных
сопряжений коренй r1,2=α±βi, то общий интеграл ур.выражается
формулой – y=eax(C1cosβx+C2sinβx)
Знакопеременный ряд сходится абсолютно если – сходится ряд
составленный из абсолютных значений его членов
Как называется и обозначается производная от функции
у=∫(х1, х2, . . . , хn) по х1 взятая в предложении, что остальные
аргументы явл.постоянными? – называется частной производной от у
𝜕у
∫(х1+𝛥х1,x2,…,хn)−∫(х1,х2,...,хn)
по х1 и обозночается
= lim =
𝜕х1
𝛥х1→0
𝛥х1
Каким методом решается уравнения n-го порядка уn=∫(х) – решается
последовательным интегрированием
Какой интеграл дифференц.уравнения называется общим – если он
содержит столько независимых произвольных постоянных, каков
порядок уравнения
Классическое определение вероятности события определяется
𝑚
равенством P(A)= – m-число элементарных исходов
𝑛
благоприятствующих появлению события А, n-общее число
возможных элементарных исходов испытания
Найти вероятность того, что в результате испытания случайная
величина Х примет значение , заключенное в интервале (0,1/3), если
она задана функцией распределения: (1/4)
0, x  1

F ( x)  (3 / 4) x  3 / 4,1  x  1 / 3
1, x  1 / 3

3
3
1, 𝑥 > 1/3
(((1/4)))
Найти общее решение дифференц.ур y’’- x+2=0
24 3
2𝑥𝑦 𝑐𝑜𝑠𝑥2 𝑦−3𝑦 2
𝑥2 𝑐𝑜𝑠𝑥2 𝑦+6𝑥𝑦
))))))
𝑘→∞
𝑥+𝑦
)))
𝑥+3𝑦
Найти решение неоднородного дифференциального уравнения y’’y=2x2+x (((Y=C1e-x+C2 ex-2x2 -x-4)))
Найти решение неоднородного дифференциального уравнения y’’y=4x2+2 (((Y=C1e-x+C2ex-4x2-10)))
Найти уравнение интегральной кривой, удовлетворяющее
дифференциальному уравнению xdx-2dy=0 с условиями y=1, при x=3:
(x2-4y-5=0 )
Найти уравнение интегральной кривой, удовлетворяющее
дифференциальному уравнению dx-2ydy=0 c условиями y=2, при х=1:
(x-y2+3=0)
Найти уравнение интегральной кривой, удовлетворяющее
дифференциальному уравнению (y-4)dx-(x+1)dy=0 с условиями y=10,
при х=1: (y-3x-7=0)
Найти уравнение интегральной кривой, удовлетворяющее
дифференциальному уравнению (x-2)dy-(y+3)dx=0с условиями у=-1,
при х=3: (y-2x+7=0)
Найти уравнение касательной плоскости к поверхности 2z=x2 -y2 в
точке А(3;1;4) (((3x-y-z=4)))
Найти уравнение касательной плоскости к поверхности x2+2y2+3z2=6 в
точке А(1;-1;1) (((x-2y+3z=6)))
Найти уравнение касательной плоскости к эллиптическому
параболоиду Z=2x2+y2 в точке A(1; -1;3) ((((4x-2y-z-3=0))))
Найти уравнение нормали к поверхности 2z=x2-y2 в точке А(3;1;4)
𝑥−3
y−1
z−4
(((
=
= )))
6
−2
−2
Найти уравнение нормали к поверхности x2+2y2+3z2=6 в точке А(1;𝑥−1
y+1
z−1
1;1) (((
=
= )))
1
−2
1
Найти уравнение нормали к эллиптическому параболоиду z=2x2+y2 в
𝑥−1
y+1
z−3
точке А(1;-1;3) (((
=
= )))
4
−2
−1
Найти уравнение семейства интегральных кривых, удовлетворяющих
дифференц. уравнению (x+xy2)dx+(y+yx2)dy=0 (( (1+x2)(1+y2)-C=0 ))
Областью определения функции z(x,y) заданной уравнением z=y2-2x-1
является (( вся плоскость хОу))
Областью распределения функции z(x,y) заданной ур. z=x2 -2xy+y2 -1
является (( вся плоскость хОу))
+∞
Областью сходимости степенного ряда ∑𝑛=0
𝑎𝑛 (𝑥 − 𝑥0)𝑛 является
((один интеграл числовой оси симметричный относительно точки х=0
который может быть закрытым открытым или полуоткрытым.))
+∞
Областью сходимости степенного ряда ∑𝑛=0
𝑎𝑛 𝑥 𝑛 является
((один интервал числовой оси , симметричный относительно точки
x=0, который может быть закрытым, открытым или полуоткрытым))
Общий интеграл линейного неоднородного ур. Y n+…+an-1y’+any=p(x)
равен (( сумме какого-либо его частного интеграла и общего интеграла
соответствующего однородного ур.получающегося при р(х)=0))
Общий интеграл линейного однородного ур.втрого порядка с
постоянными коэфф.находится с помощью ((характеристического
уравнения))
Определить область сходимости функционального ряда
𝑋3
√2
+. . . +
𝑋𝑛
√2
𝑋
√2
+
𝑋2
√2
+
+. ..: (-1<x<1)
𝑛
Определить область сходимости функционального ряда ∑∞
𝑛=0 2𝑥 :
(-1<x<1)
𝑛
Определить область сходимости функционального ряда ∑∞
𝑛=0 𝑥 /2:
(-1<x<1)
𝑛
Определить область сходимости функцион-го ряда ∑∞
𝑛=0(𝑥 − 3) /5:
(2<x<4)
Определить область сходимости функционального ряда
x+x2+x3+…+xn+…: (-1<x<1)
𝑛−1
𝑛
Определить радиус сходимости ряда ∑∞
𝑛=0 𝑛 (𝑥 − 2) : (3)
Определить радиус сходимости ряда ∑∞
𝑛=0
Определить радиус сходимости ряда ∑∞
𝑛=0
Определить радиус сходимости ряда ∑∞
𝑛=0
3
𝑛𝑥𝑛
: (4)
4𝑛
𝑛(𝑥−2)𝑛
4𝑛
𝑛𝑥𝑛
: (4)
: (5)
5𝑛
𝑛(𝑥−1)𝑛
∑∞
:
𝑛=0
5𝑛
2
2
Определить радиус сходимости ряда
(5)
Определить экстремум функции z=(x-1) +4y (((zmin=P(1;0))))
Определить экстремум функции z=2x2 -4x+3y2 (((Zmin=P(1;0))))
Переменная у называется неявной функцией от независимых
переменных x1,x2,…,xn, если – она задана уравнением
∫(х1, х2, . . . , хn)=0 которое не разрешено относительно у
Переменная у называется функцией n-переменных(аргументов)
х1,х2,...,хn,если – каждой системе значений х1,х2,...,хn из области их
изменения соответствует опред.значение у.
Полный дифференциал dy функции у=∫(х1, х2, . . . , хn) равен –
𝜕у
𝜕у
dy=dx1y+ dx2y+…+ dxny= 𝑑𝑥1 + ⋯ + 𝑑𝑥𝑛
𝜕х1
𝜕х𝑛
Полный дифференциал dy функции у=∫(х1, х2, . . . , хn)называется –
главная часть его полного приращения dу=∫(х1 + 𝛥х1, x2 +
𝛥х1, … , хn + 𝛥х𝑛) − ∫(х1, х2, . . . , хn), линенйная относительно
приращений 𝛥х1,… 𝛥х𝑛
Полным дифференциалом функции у=∫(х1, х2, . . . , хn) называется
главная часть его полного приращения dx2=∫(х1 + 𝛥х1, x2 +
𝛥х1, … , хn + 𝛥х𝑛) − ∫(х1, х2, . . . , хn), линейная относительно
приращений 𝛥х1,… 𝛥х𝑛
Порядком дифференциального уравнения называется – порядок
высшей производной, содержавшейся в этом уравнении
𝑎𝑘+1
Пусть дан ряд с положительными членами ∑∞
=p ряд
𝑘=0 𝑎𝑘 и lim
𝑘→∞ 𝑎𝑘
сходится если (( p<1))
Ряд называется сходящимся если – сумма n первых его членов при
n∞ имеет конечный предел
Ряд сходится безусловно если (( ряд сходится и любая его
перестановка не нарушает его сходимости))
Ряд сходится условно если (( ряд сходится но существует перестановка
его членов нарушающая его сходимость ))
Совокупность всех точек, в которых функция многих переменных
имеет определенные действительные значения называют ((областью
определения(существования)))
Согласно необходимому признаку сходимости ряда lim 𝑎𝑛 = 0, где
𝑛→∞
∞ 1
𝑛=1 𝑛:
a n -общий член ряда, ряд ∑
(сходится)
Согласно необходимому признаку сходимости ряда lim 𝑎𝑛 = 0, где
𝑛→∞
2𝑛+1
-общий член ряда, ряд ∑∞
𝑛=1 3𝑛2 +5: (сходится)
n
Согласно необходимому признаку сходимости ряда lim 𝑎𝑛 = 0, где
a
𝑛→∞
она задана функцией распределения F(x)={(4) 𝑥 + 4 , −1 < 𝑥 ≤ 1/3
𝑥4 𝑥3
)))
an
-
6𝑛2 +7𝑛+1
Найти вероятность того, что в результате испытания случайная
величина Х примет значение, заключённое в интервале(0, 1/3), если
0, 𝑥 ≤ −1
((y=
𝑥+6𝑥2 𝑦
Найти производную неявной функции x2+2xy+3y2=0 (((−
𝜕𝑧(1;2)
𝜕𝑦
3
𝑦+4𝑥𝑦 2 +6𝑥𝑦 2
Найти производную неявной функции sinx2y+3xy2=0
𝜕𝑧(0;2)
𝜕𝑥
Уравнение первого порядка у’=∫(х, у)называется однородным если
((функцию ∫(х, у) можно представить как функцию только одного
у
отношения переменных ∫(х, у) =φ( )))
х
Формула радиуса сходимости по Даламберу имеет вид –
𝑎𝑘+1
((R = lim |
|))
Найти производную неявной функции 2xy-exy+y=0 ((( 𝑥𝑦
)))
𝑥𝑒 −2𝑥−1
Найти производную неявной функции ln xy+2x2+6xy=0
: (3/2)
:: (0)
𝜕𝑥
𝜕𝑧(3;−1)
z=x4+6x3+2y-3 Найти
𝑥−𝑦
2y−yexy
𝜕𝑧(1;0)
𝜕𝑥
𝜕𝑧(0;1)
+ 𝐶1𝑥 2+C2x+C3))
5
Найти общее решение дифференц.ур y’’-5=0 (( y= x3+C1x2+C2x+C3))
6
Найти общее решение дифференциального уравнения y’’+4y’+3y=0:
(y=C1e-x+C2 e-3x)
Найти общее решение дифференциального уравнения y’’-5y’+6y=0:
(y=C12ч+C2e3x)
Найти общее решение дифференциального уравнения y’’-25y=0
(y=C1e-5+C2e5)
Найти общий интеграл линейного дифференциального уравнения
y’-y=ex ((( y=ex(x+C) )))
Найти общий интеграл линейного дифференциального уравнения y’y=e2x ((( y=ex(ex+C) )))
Найти общий интеграл однородного дифференциального уравнения
xdy-(x+y)dx=0: y=x(lnx+C)
Найти общий интеграл однородного дифференциального уравнения
xdy-(x+2y)dx=0: (y+x=Cx2)
Найти общий интеграл однородного дифференциального уравнения
xdy-(x-y)dx=0; (y=xlnC/x))
Найти общий интеграл однородного дифференциального уравнения
xdy+(x-y)dx=0; (y=xlnC/x)
Найти общий интеграл однородного дифферициального уравнения
𝑥
x2dy-(x2+y2 -xy)dx=0 (((
− 𝑙𝑛𝑥 = 𝐶)))
𝑥−𝑦
Найти плотность распределения непрерывной случайной величины Х,
0, 𝑥 ≤ 0
если она задана функцией распределения F(x)={𝑠𝑖𝑛𝑥, 0 < 𝑥 ≤ пи/2
1, 𝑥 > пи/2
0, 𝑥 < 0
(((F(x)={𝑐𝑜𝑠𝑥, 0 < 𝑥 ≤ пи/2)))
0, 𝑥 > пи/2
Найти полный дифференциал dz функции z=2xy+y2
((dz=2ydx+2(x+y)dy))
Найти полный дифференциал dz функции z=lnx+y2: ((dz=1/xdx+2ydy))
Найти полный дифференциал dz функции z=sinxy+x2
((dz=(ycosxy+2x)dx+xcosxydy))
Найти полный дифференциал dz функции z=cosxy+x
((dz=(-ysinxy+1)dx-xsinxydy))
Найти полный дифференциал dz функции z=sinx+xy2
((dz=(cosx+y2)dx+2xydy))
общий член ряда, ряд ∑∞
: (расходится)
𝑛=1
𝑛2 +1
Согласно необходимому признаку сходимости ряда lim 𝑎𝑛 = 0, где
an
-общий член ряда, ряд ∑∞
𝑛=1
3𝑛2 +5
𝑛→∞
: (расходится)
(4𝑛+1)2
Согласно необходимому признаку сходимости ряда lim 𝑎𝑛 = 0, где
𝑛→∞
(2𝑛+1)2
-общий член ряда, ряд ∑∞
𝑛=1 𝑛+1 : (расходится)
n
Укажите какая функция называется интегралом дифференц.уравнения
((функция удовлетворяющая дифференц.уравнению, т.е.обращающая
его в тождество))
Укажите какое из ниже приведенных определений правильно
определяет понятие дифференц.уравнения (( дифференц.уравнением
называется равенство, содержащие производные или дифференциалы
неизвестной функции))
Укажите неверное утверждение (( ряд Тейлора можно записать для
любой функции даже если она не имеет производные любого порядка))
Укажите неверное утверждение(((Математическое ожидание
биномиального распределения равна произведению числа испытаний
на вероятности появления и не появления события в одном
испытании:М(Х)=npq)))
Укажите правильное утверждение –всякий абсолютно сходящийся ряд
есть ряд сходящийся
Укажите правильный метод решения линейного уравнения первого
порядка вида у’+Р(х)у=Q(x) – линейное уравнение решается
посредством замены функции у=uv, откуда y’=u’v+uv’
Укажите правильный метод решения однородного уравнения первого
порядка вида у’=∫(х, у) - однородное ур.приводится к ур. с
разделяющими переменными и решается посредством замены функции
у (или х) новой функцией и по формуле у=uх (или х=uу)
(−1)𝑛+1
Укажите сходимость или расходимость ряда ∑∞
𝑛=1
2
a
𝑛
(((абсолютно сходится)))
(−1)𝑛+1
Укажите сходимость или расходимость ряда ∑∞
𝑛=1 𝑛2 4 𝑛
(((абсолютно сходится)))
(−1)𝑛+1
Укажите сходимость или расходимость ряда ∑∞
𝑛=1 𝑛2 2𝑛
(((абсолютно сходится)))
(−1)𝑛+1
∞
Укажите сходимость или расходимость ряда ∑𝑛=1
(((Условно сходится)))
√𝑛
(−1)𝑛+1
Укажите сходимость или расходимость ряда ∑∞
𝑛=1
𝑛
(((Условно сходится)))
𝑛!
Укажите сходимость или расходимость ряда ∑∞
𝑛=1 𝑛 : (расходится)
3
2𝑛
Укажите сходимость или расходимость ряда ∑∞
𝑛=1 𝑛3𝑛:: (сходится)
Уравнение первого порядка Р(х,у)dx+Q(x,y)dy=0 называется уравнение
с разделяющимися переменными, если – функции Р и Q разлагаются
на множители, зависящие только от одной переменной
𝑎𝑘
Функции F(x,y,Ci)=0 уравнения Ф(x,y,y’,y’’,…,yn)=0 называеются
((семейством интегральных кривых))
Функция распределения F(х) случайной величины Х определяет (( для
каждого значения х вероятность того что случайная величина Х
примет значение меньше х, т.е. F(x)=P(X<x)))
Функция у=φ(х,Сi)уравнения Ф(х,у,у’,y’’,…,yn)=0 называется (( общим
интегралом дифференц.уравнения))
Частным дифференциалом функции у=∫(х1, х2, . . . , хn)по х1
называется – главная часть соответствующего частного приращения
dx2=∫(х1 + 𝛥х1, x2, … , хn) − ∫(х1, х2, . . . , хn), линейная относительно
приращения 𝛥х1
Чему равна сумма первых трех членов ряда Маклорена разложения
функции cos1: (13/24)
Чему равна сумма первых трех членов ряда Маклорена разложения
функции cos2: (-1/3)
Чему равна сумма первых трех членов ряда Маклорена разложения
функции sin 1? (((101/120)))
Чему равна сумма первых трех членов ряда Маклорена разложения
функции sin 2? (((14/15)))
Чему равна сумма первых трех членов ряда Маклорена разложения
функции e3? (((17/2)))