Кравченко Т.К.¹, Авдеев Ю.В.² Высшая школа экономики, Москва

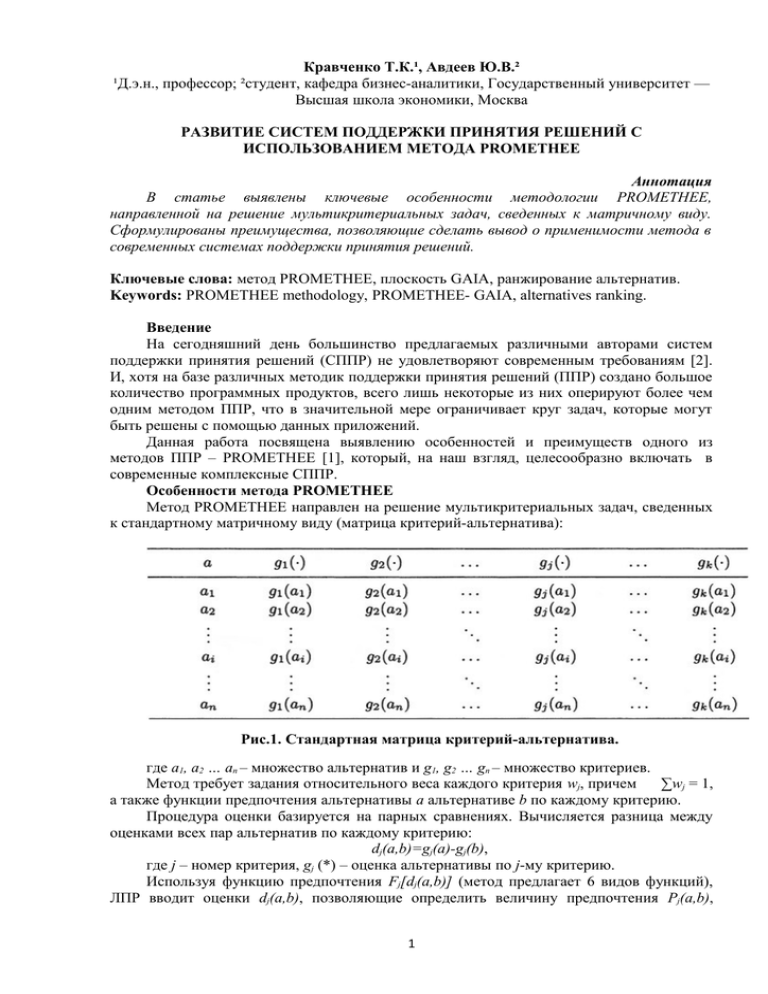
Кравченко Т.К.¹, Авдеев Ю.В.²
¹Д.э.н., профессор; ²студент, кафедра бизнес-аналитики, Государственный университет —
Высшая школа экономики, Москва
РАЗВИТИЕ СИСТЕМ ПОДДЕРЖКИ ПРИНЯТИЯ РЕШЕНИЙ С
ИСПОЛЬЗОВАНИЕМ МЕТОДА PROMETHEE
Аннотация
В статье выявлены ключевые особенности методологии PROMETHEE,
направленной на решение мультикритериальных задач, сведенных к матричному виду.
Сформулированы преимущества, позволяющие сделать вывод о применимости метода в
современных системах поддержки принятия решений.
Ключевые слова: метод PROMETHEE, плоскость GAIA, ранжирование альтернатив.
Keywords: PROMETHEE methodology, PROMETHEE- GAIA, alternatives ranking.
Введение
На сегодняшний день большинство предлагаемых различными авторами систем
поддержки принятия решений (СППР) не удовлетворяют современным требованиям [2].
И, хотя на базе различных методик поддержки принятия решений (ППР) создано большое
количество программных продуктов, всего лишь некоторые из них оперируют более чем
одним методом ППР, что в значительной мере ограничивает круг задач, которые могут
быть решены с помощью данных приложений.
Данная работа посвящена выявлению особенностей и преимуществ одного из
методов ППР – PROMETHEE [1], который, на наш взгляд, целесообразно включать в
современные комплексные СППР.
Особенности метода PROMETHEE
Метод PROMETHEE направлен на решение мультикритериальных задач, сведенных
к стандартному матричному виду (матрица критерий-альтернатива):
Рис.1. Стандартная матрица критерий-альтернатива.
где a1, a2 … an – множество альтернатив и g1, g2 … gn – множество критериев.
Метод требует задания относительного веса каждого критерия wj, причем
∑wj = 1,
а также функции предпочтения альтернативы a альтернативе b по каждому критерию.
Процедура оценки базируется на парных сравнениях. Вычисляется разница между
оценками всех пар альтернатив по каждому критерию:
dj(a,b)=gj(a)-gj(b),
где j – номер критерия, gj (*) – оценка альтернативы по j-му критерию.
Используя функцию предпочтения Fj[dj(a,b)] (метод предлагает 6 видов функций),
ЛПР вводит оценки dj(a,b), позволяющие определить величину предпочтения Pj(a,b),
1
которая показывает насколько альтернатива a лучше альтернативы b (если a хуже b, тогда
Pj(a,b)=0):
Pj(a,b) = Fj[dj(a,b)], где 0<=Pj(a,b)<=1.
На Рис.1 приведен наиболее распространенный случай задания функции
предпочтения, с помощью которой может быть произведена оценка dj(a,b), где q –
определенное значение dj(a,b), достигнув которого альтернатива a становится лучше
альтернативы b, т. е величина P становится равной 1. В данном примере функция
предпочтения строгая, т.е. P равняется либо 0, либо 1, но в других случаях величина P
может быть дробной. Для некоторых функций предпочтения также необходимо
определить величину p – определенное значение dj(a,b), достигнув которого альтернатива
a становится строго лучше альтернативы b (т.е. Pj(a,b) = 1).
Type
P 2:
Ushape
1
Criterion
0
q=p
d
Рис.2. Пример задания функции предпочтения.
После вычисления величин P для каждой пары альтернатив по каждому критерию
необходимо вычислить агрегированные индексы предпочтений:
π(a,b)=∑ Pj(a,b)* wj
π(b,a)=∑ Pj(b,a)* wj (обратная величина)
PROMETHEE I Partial Ranking.
Далее для сравнения альтернатив вычисляются положительный и отрицательный
восходящие потоки: φ+ и φ-:
φ+(a) = ∑ π(a,x) /(n-1); φ-(а) = ∑ π(x,a) /(n-1),
где n – общее количество альтернатив, x – все остальные альтернативы, кроме
исследуемой альтернативы a. Величина φ+(a) показывает, как альтернатива a соотносится
с остальными альтернативами (лучше или хуже), φ-(а) - как остальные альтернативы
соотносятся с альтернативой а. Т.е. чем больше φ+(a), тем лучше альтернатива и,
соответственно, чем больше φ-(а), тем она хуже. Графически φ+ и φ- можно изобразить
следующим образом (Рис.3):
2
Рис 3. Положительный и отрицательный восходящий потоки.
Вычислив положительный и отрицательный восходящие потоки можно произвести
процедуру частичного ранжирования альтернатив. Зачастую, оценки φ + (.) и φ- (.) дают разный
результат, поэтому необходимо комплексно учитывать оба этих показателя. Согласно
ранжированию PROMETHEE I, альтернатива a лучше альтернативы b, если:
φ+(a)> φ+(b) и φ - (а)< φ-(b), или
φ+(a)= φ+(b) и φ - (а)< φ-(b), или
φ+(a)> φ+(b) и φ- (а)= φ-(b);
альтернативы a и b безразличны, если:
φ+(a)> φ+(b) и φ- (а)= φ-(b);
альтернативы a и b невозможно сравнить, если:
φ+(a)> φ+(b) и φ- ( а> φ-(b), или
φ+(a)< φ+(b) и φ- (а)< φ-(b).
PROMETHEE II Ranking.
Процедура оценки PROMETHEE II базируется на вычислении «чистых восходящих
потоков», получаемых с помощью вычисления разности между положительным и
отрицательным восходящими потоками: φ(a) = φ+(a) - φ-(а), где φ(a) – чистый
восходящий поток. Чем величина чистого восходящего потока выше, тем лучше
альтернатива.
Несмотря на то, что полное ранжирование PROMTHEE II несложно выполнить, и
получить конечный и точный результат, создатели метода рекомендуют учитывать также
и частичное ранжирование PROMETHEE I, т.к. анализ несравнимых альтернатив
(согласно частичному ранжированию) может помочь в принятии правильного решения.
Специфика визуального отображения оценки вариантов решений методом
PROMETHEE
Отображая информацию об альтернативах и их оценках по каждому из критериев на
плоскости, мы можем наглядно продемонстрировать, какая из альтернатив доминирует по
определенным критериям. Для создания подобной плоскости (авторское название Geometrical Analysis for Interactive Assistance (GAIA)) необходимо спроецировать
альтернативы на плоскость в виде точек, а критерии в виде векторов.
Для того чтобы модифицировать плоскость GAIA, можно включить в нее вектор
весов, который можно получить исходя из относительного веса каждого критерия (длины
вектора, отображающего данный критерий). Вектор весов необходим ЛПР для того, чтобы
лучше понять общую картину мультикритериальной проблемы.
На рис. 4 продемонстрирован вариант построения плоскости GAIA, где Ci – проекция
вектора i-го критерия, Ai – проекция i-ой альтернативы, вектор π – проекция вектора весов
на плоскость GAIA. Согласно графику, наибольший вес имеют критерии №1 и 3, в то
время как вес критерия №2 практически равен 0.
Альтернатива A1 является оптимальным решением, но также высокие показатели по
наиболее важным критериям имеют альтернативы A5 и A6.
Рис 4. Плоскость GAIA
3
Преимущества методики PROMETHEE
В проведенном исследовании выявлены преимущества и характерные особенности
метода PROMETHEE:
1) Метод позволяет найти единственное решение, а также составить иерархический
список альтернатив.
2) Наличие четкой и прозрачной методики отбора.
3) Минимальный и интуитивно понятный набор дополнительных данных.
4) Возможность визуального отображения оценок вариантов решений, позволяющей
ЛПР наглядно представить себе сильные и слабые стороны каждой из альтернатив.
5) Возможность оценки не только отдельных, но также и наборов альтернатив.
Заключение
Создание современных СППР обеспечит управленцам любого уровня мощную
логическую поддержку практически в любой сфере деятельности: от банковской и
финансовой сфер до политической деятельности и принятия сложных решений
государственной важности.
Так как ни один метод по отдельности не дает исчерпывающего и применимого при
любых обстоятельствах способа поиска наилучшего решения проблемы, стоит вопрос
создания комплексных СППР, включающих в себя различные методики оценки
альтернатив. При этом методы, которые будут включены в комплексные СППР, должны
пройти жесткий отбор с целью выявления наиболее эффективных и взаимодополняющих
методик.
Методика PROMETHEE способна дополнить такие известные методологии, как
метод анализа иерархий Томаса Саати и семейство методов Electre, а также и другие
методики, обеспечив визуализацию мультикритериальной проблемы и выявление схожих
по своей эффективности отдельных или наборов альтернатив. Методика достаточно
проста в использовании, и, соответственно, требует минимального набора
дополнительных знаний для того, чтобы проводить оценку альтернатив.
Литература
1. Figueira J., Greco S., Ehrgott M. - Multiple Criteria Decision Analysis[c] State of the Art
Surveys. - 2004. - С. 200-232.
2. Информация сайта «Программные системы поддержки оптимальных решений». Режим доступа: http://www.tomakechoice.com/tchoice.html.
3. Информация сайта «Программные системы поддержки оптимальных решений». Режим доступа: http://www.tomakechoice.com/optimum.html.
4. Принятие решений при многих критериях, В.Д. Ногин, Учебно-методическое пособие. Режим доступа: http://www.apmath.spbu.ru/ru/staff/nogin/nogin_u11.pdf
4