486 ПОЛУЧЕНИЕ ПОРОШКОБРАЗНОГО НИТРИДА ТИТАНА В

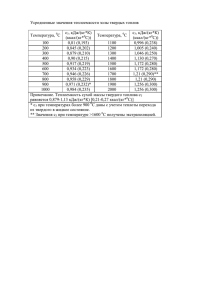
XV Международная научно-практическая конференция «СОВРЕМЕННЫЕ ТЕХНИКА И ТЕХНОЛОГИИ»
ПОЛУЧЕНИЕ ПОРОШКОБРАЗНОГО НИТРИДА ТИТАНА
В ГИПЕРСКОРОСТНОЙ ПЛАЗМЕННОЙ СТРУЕ
Евдокимов А.А., Шеметов Д.Д.
Научный руководитель: Сивков А.А., д.т.н., профессор
Томский политехнический университет, 634050, Россия, г. Томск, пр. Ленина, 30
E-mail: Evd.Andrew@gmail.com
В работах [1] показана возможность динамического синтеза и получения ультрадисперсного
порошка (УДП) высокотвердого и термостойкого кристаллического нитрида титана TiN в гиперскоростной струе электроразрядной плазмы.
Основной рабочий материал – титан – перерабатывается электроэрозионным путем с поверхности ускорительного канала (УК) титанового
ствола коаксиального магнитоплазменного ускорителя (КМПУ). Импульсное электропитание
КМПУ осуществляется от емкостного накопителя энергии (ЕНЭ).
Синтез TiN происходит во фронте головной
волны с последующим распылением, кристаллизацией и формированием из жидкой фазы
частиц дисперсного материала.
Производительность системы по наработке
материала электроэрозионным путем определяется величиной энергии, выделившейся в УК
КМПУ. На рис. 1 приведены типичные осциллограммы импульса рабочего тока i(t) и напряжения на электродах ускорителя U(t) (а), по которым определяется подведенная энергия W (б).
Масса наработанного и вынесенного из УК
плазменной струей материала m определялась
взвешиванием титанового ствола до и после
проведения процесса.
Общая закономерность электроэрозионной
наработки титана [2] при диаметре УК
15 ≤ dУК ≤ 21 мм, дополненная данными, полученными в диапазоне подведенной энергии W
до 200 кДж, представлена на рис. 2. в виде зависимости удельной эродированной массы m/W
[г/кДж] от удельной подведенной энергии
W/VУК [кДж/см3] (VУК – объем УК).
Она аппроксимируется линейной функцией
Синтезированный продукт собирался из камеры-реактора после охлаждения до нормальной температуры и полного осаждения взвешенных в азотной атмосфере (Р0=1 атм) дисперсных частиц.
Собранный в специальной серии экспериментов продукт динамического синтеза разделялся путем просеивания на две фракции: УДП
сине-черного цвета, крупные частицы и большие куски золотистого цвета из затвердевшего
расплава. На рис. 3 приведены зависимости эродированной массы m, массы порошкообразного
продукта mУДП и массы крупных частиц и кусков mКР, от величины подведенной энергии в
специальной серии опытов.
Увеличение подведенной энергии, что очевидно, приводит к увеличению массы как ультрадисперсной фракции нитрида титана, так и к
увеличению массы «паразитной» фракции
крупных частиц и кусков материала, который,
судя по окраске, так же содержит TiN. Однако,
при этом доля крупной фракции в рассматриваемом энергетическом диапазоне увеличивается с ~10% до 25%. Отсюда следует очевидный
вывод о целесообразности проведения процесса
при относительно низкой энергетике единичного импульса.
U,кВ
2.8
2.0
1.0
t,мкс
100
0
100
100
200
225
а)
i,кА
400
200
0
600
t, мкс
200
t1
400
б)
W = ∫ U (t ) ⋅ i (t )dt
0
P, кВА
Рис. 1. Типичные осциллограммы импульса
рабочего тока i(t) и напряжения на электродах
ускорителя U(t) (а), и кривая мощности (б).
За срезом УК формируется гиперскоростная
плазменная струя, истекающая в камеруреактор, заполненную газообразным азотом.
486
Секция 12: Наноматериалы, нанотехнологии и новая энергетика титана низкоскоростным течением на хвостовой
части импульса рабочего тока, скорость которого недостаточна для распыления материала.
m/W, г/кДж
0.4
⎛ W
⎞
m
= 0.161⋅ ⎜
− 0.385 ⎟
W
⎝ VУК
⎠
0.3
0.2
0.1
0
0.5
1.0
1.5
Рис. 4. Микроэлектронные фотографии УДП
полученных при: а) W=93 кДж, P0=1 атм.
б) W=120 кДж, P0=1 атм. в) W=100 кДж, P0=2 атм.
W/VУК, кДж/см3
Рис. 2. Зависимость удельной эродированной
массы m/W [г/кДж] от удельной подведенной
энергии W/VУК [кДж/см3]
Структурно-фазовые исследования продукта
синтеза проведены методами рентгеновской
дифрактометрии, которые показали, что основными кристаллическим фазами являются нитрид титана TiN, титан Ti и диоксид титана TiO2.
При чем при изменении подведенной энергии от
93 кДж до 186 кДж и внешнем давлении азотной атмосферы P0=1 атм. содержание TiN в
УДП фракции увеличивается от 81% до 91%,
содержание Ti уменьшается от 4% до 1% и содержание TiO2 уменьшается от 15% до 8%. В
крупной фракции содержание TiN увеличивается от 45% до 83%. Содержание Ti уменьшается
от 38% до 7% и TiO2 уменьшается от 17% до
10%. Существенное увеличение содержания TiN
в УДП фракции до 99% обеспечивается при
внешнем давлении P0=2 атм.
Анализ дифрактограмм показал уменьшение
среднего размера области когерентного рассеяния (ОКР) по которому можно судить о среднем
размере частиц от ~200 нм до ~100 нм в диапазоне изменеия подведенной энергии до ~120
кДж. При дальнейшем увеличении давления
средний размер ОКР остается неизменным. Это
подтверждается и результатами исследования
порошкообразной фракции методами просвечивающей электронной микроскопии (рис. 4)
Суммируя вышесказанное можно заключить,
что основными факторами, влияющими на качество УДП, являются давление в камере-реакторе
и подведенная энергия.
Увеличение подведенной энергии, что очевидно, приводит к увеличению массы как ультрадисперсной фракции нитрида титана, так и к
увеличению массы «паразитной» фракции
крупных частиц и кусков материала, который,
судя по окраске, так же содержит TiN. Однако,
при этом доля крупной фракции в рассматриваемом энергетическом диапазоне увеличивается с ~10% до 25%
20
m, г
1
15
2
10
5
3
0
80
100
120
140 W, кДж
Рис. 3. Зависимости эродированной m (1), массы
порошкообразного продукта mУДП (2) и массы
крупных частиц и кусков mКР (3), от величины
подведенной энергии
ЛИТЕРАТУРА:
1. Сивков А.А., Найден Е.П., Герасимов
Д.Ю. Прямой динамический синтез нанодисперсного нитрида титана в высокоскоростной
импульсной струе электроразрядной плазмы //
Сверхтвердые материалы. – 2008. – №5. – С. 3339
Отсюда следует очевидный вывод о целесообразности проведения процесса при относительно низкой энергетике единичного импульса.
Наиболее вероятной причиной образования
крупной фракции в продукте динамического
синтеза является вынос из УК расплавленного
487
XV Международная научно-практическая конференция «СОВРЕМЕННЫЕ ТЕХНИКА И ТЕХНОЛОГИИ»
2. Сивков А.А., Герасимов Д.Ю., Цыбина А.С.
Электроэрозионная наработка материала в
КМПУ для нанесения покрытий // «Электротехника». – 2005 г. – №6. – С.25-33
ВЛИЯНИЕ БРОУНОВСКОГО ДВИЖЕНИЯ НАНОЧАСТИЦ AL2O3
НА ИХ СЕДИМЕНТАЦИЮ В СЛАБОКОНЦЕНТРИРОВАННОЙ СУСПЕНЗИИ
Животков А.В., Чернов Ф.Н.
Научный руководитель Малинин В.И., д.т.н., профессор
Пермский государственный технический университет,
614000, г. Пермь, Комсомольский проспект, 29
E-mail: felistigris@mail.ru
Наиболее целесообразным способом выделения оксида алюминия с заданной дисперсностью из конденсированных продуктов сгорания
является осаждение свободных частиц в слабоконцентрированной стабильной суспензии (частицы не сталкиваются друг с другом и движутся
по вертикали) [1]. Этот метод (седиментация)
основан на большом отличии времён оседания
крупных и мелких частиц.
В данной работе рассматривается седиментация наночастиц Al2O3 в жидкости с учётом их
броуновского движения.
Рассматриваемый процесс можно описать
обезразмеренным уравнением Эйнштейна –
Колмогорова [2, 3]:
∂p
∂p ∂ 2 p
+A ,
=
∂z
∂τ ∂z 2
dp
d 2 pe
+ A e = 0 . (3)
2
dz
dz
Решая уравнение (3), получим значения
равновесной функции дифференциального распределения наночастиц по безразмерной высоте
z (определяет вероятность нахождения частиц
на высоте z):
pe = Be − Az ,
где коэффициент В определяется из условия
нормировки функции pe.
Введем равновесную функцию Pe интегрального распределения наночастиц по высоте z
(определяет вероятность нахождения частиц в
диапазоне высот 0 – z):
(1)
z
Pe ( z ) = ∫ pe dz =
где p – вероятность нахождения частиц на безразмерной высоте z, z = h/H (h – текущая высота, Н – высота слоя жидкости), τ – текущее безразмерное время ( τ = t / τ D , t – текущее время,
τD – время диффузии частиц). Параметр А определяет отношение времени диффузии τD ко времени оседания τF:
τ D = H / D = H /(bkT ),
τ F = H /(bF ) = H / U ,
A = τ D / τ F = HF / kT .
2
(4)
0
B
(1 − e − Az ) .
A
(5)
Если заданы конкретные значения функции
Pe*, то, используя формулы (4) и (5), можно
найти соответствующие им значения высоты z*:
z* = ln(1 −
2
(2)
Pe* A
)/ A.
B
(6)
Зависимость z* от параметра А (при заданных значениях Pe*), рассчитанная по формуле
(2)
(6) представлена
на рис. 1.
здесь D, b – соответственно коэффициенты
диффузии и подвижности частиц в жидкости, k
– постоянная Больцмана, Т – температура суспензии, F – результирующая сил, действующих
на частицу, U – скорость оседания частиц.
При времени τ → ∞ значения функции р
уравнения (1) стремятся к значениям равновесной функции pе , которая описывается уравнением:
488