1. Метод Ньютона для решения нелинейного уравнения и систем
реклама

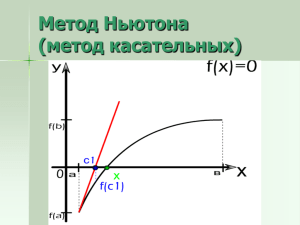
Варианты для задания 1.1 1. 1.1. Варианты для задания 1.2 Метод Ньютона для решения нелинейного уравнения и систем Метод Ньютона (метод касательных) для решения нелинейного уравнения Пусть дано уравнение f (x) = 0 (1) и начальное приближение x0 к его корню. Предполагаем, что функция f (x) — вещественная и находим вещественный корень x∗ . Будем предполагать, что на отрезке [a, b] (x0 ∈ [a, b]) содержится единственный корень уравнения (1) и существуют непрерывные производные f 0 (x) 6= 0, f 00 (x) 6= 0. Заменим уравнение в окрестности x0 приближенно уравнением f (x0 ) + f 0 (x0 )(x − x0 ) = 0, левая часть которого есть линейная часть разложения функции f (x) в ряд Тейлора в окрестности точки x0 . Отсюда x1 = x0 − f (x0 ) f 0 (x0 ) . Действуя аналогично, получаем расчетную формулу метода Ньютона xk = xk−1 − f (xk−1 ) , k = 1, 2, . . . . f 0 (xk−1 ) (2) Метод Ньютона имеет простой геометрический смысл: xk есть абсцисса точки пересечения касательной к графику функции f (x), построенной в точке (xk−1 , f (xk−1 )), с осью абсцисс. Теорема 1 (о сходимости). Если 1. f (a)f (b) < 0, 2. f 0 (x), f 00 (x) отличны от нуля (сохраняют определенные знаки при 3. f (x0 )f 00 (x0 ) > 0, x0 ∈ [a, b], то xk → x∗ , причем скорость сходимости определяется неравенством M2 |xk − x∗ | ≤ (xk−1 − x∗ )2 . 2m1 Здесь m1 = min |f 0 (x)|, M2 = max |f 00 (x)|. x∈[a,b] x ∈ [a, b]), x∈[a,b] Если f (x0 ) f 00 (x0 ) < 0, то можно не прийти к x = x∗ , если x0 не очень хорошее. Заметим, что если f 0 (x∗ ) = 0, то квадратичной сходимости может и не быть. Например, пусть f (x) = x2 , корень x∗ = 0 — корень второй кратности, расчетная формула имеет вид: xk+1 = xk /2 и сходимость линейная. Иногда целесообразно применять модифицированный метод Ньютона с расчетной формулой: xk = xk−1 − f (xk−1 ) , k = 1, 2, . . . f 0 (x0 ) (3) Скорость сходимости модифицированного метода значительно меньше. При решении задачи итерационными методами следует обращать внимание на следующие моменты: 1 • расчетная формула; • условие сходимости; • скорость сходимости; • получение решения с заданной точностью ε. В методе Ньютона можно пользоваться следующим критерием: если |xk+1 − xk | < ε, то |xk − x∗ | < ε. Задание 1.1 Дано уравнение f (x) = 0. Требуется найти все решения уравнения или решения на заданном промежутке с заданной точностью ε = 0.00001. Программа должна содержать подпрограмму для уточнения решения методом Ньютона с параметрами: • x0 — нулевое приближение к корню; • ε — заданная точность; • kmax — максимальное количество итераций (для исключения зацикливания). Подпрограмма должна возвращать либо xk , такое что |xk − xk−1 | < ε, либо xk max . Отчет по выполнению задания должен содержать: • график функции f (x) для нахождения начального приближения; • уточнение начального приближения до тех пор, пока |xk − xk−1 | < ε, методом Ньютона по формуле (2). • уточнение начального приближения до тех пор, пока |xk − xk−1 | < ε, модифицированным методом Ньютона по формуле (3). Сравнить результаты, количество итераций. Возможно, начальное приближение придется уточнить прежде методом половинного деления. Результаты оформить в виде таблицы 1. k 0 1 ... 1.2. Таблица 1 xk -xk−1 f(xk ) — xk ... ... ... Метод Ньютона для решения системы 2-х уравнений Дана система: ( f (x, y) = 0, (4) g(x, y) = 0. где f (x, y), g(x, y) достаточно гладкие функции. В результате действий, аналогичных случаю одного уравнения, т.е. приближенно заменяя систему (4) линейной системой, получаем следующие расчетные формулы: (k) xk+1 = xk − (k) dx dy d d(k) , yk+1 = yk − (k) где 2 , (k) d f (x , y ) (k) dx = g (x k, y k) k k f 0 (x , y ) f 0 y (xk , yk ) k k x , = 0 g x (xk , yk ) g 0 y (xk , yk ) f 0 y (xk , yk ) (k) f 0 x (xk , yk ) , d = y 0 g 0 x (xk , yk ) g y (xk , yk ) f (xk , yk ) g (xk , yk ) . Задание 1.2 Требуется найти все решения системы уравнений или решения в заданной области с заданной точностью ε=0.00001. Программа должна содержать подпрограмму для уточнения решения методом Ньютона с параметрами: x0 , y0 — нулевое приближение к корню; ε — заданная точность; kmax — максимальное количество итераций (для исключения зацикливания). Подпрограмма должна возвращать либо решение (xk , yk ), такое что ||(xk − xk−1 , yk − yk−1 )|| < ε, либо (xk max , yk max ). Здесь норма вектора (xk − xk−1 , yk − yk−1 ) может быть вычислена, например, следующим образом: p ||(xk − xk−1 , yk − yk−1 )|| = (xk − xk−1 )2 + (yk − yk−1 )2 . Отчет должен содержать Графики функций f (x, y) = 0, g(x, y) = 0 для выбора начального приближения, выполненные в математическом пакете Maple. Уточнение начального приближения до тех пор, пока ||(xk − xk−1 , yk − yk−1 )|| < ε, методом Ньютона. Результаты оформить в виде таблицы 2. k 0 1 ... xk yk ||((xk − xk−1 ), (yk − yk−1 ))|| — Варианты для задания 1.1 f (xk , yk ) Таблица 2 g(xk , yk ) Варианты для задания 1.2 3