( ) ( ) { ( )s ( ) s ( ) 0 ( ) - НИИ прикладных проблем математики и

ВЕРОЯТНОСТНО-СТАТИСТИЧЕСКИЕ СВОЙСТВА ЦЕПЕЙ МАРКОВА ПЕРЕМЕННОГО ПОРЯДКА
1
ВЕРОЯТНОСТНО-СТАТИСТИЧЕСКИЕ СВОЙСТВА ЦЕПЕЙ
МАРКОВА ПЕРЕМЕННОГО ПОРЯДКА
М.В. Мальцев
Учреждение Белорусского государственного университета «НИИ прикладных проблем
математики и информатики», НИЛ математических методов защиты информации
Минск, Республика Беларусь
телефон: +(37529)2785526; e-mail: maltsew@mail.ru
последовательность
1 АННОТАЦИЯ
Рассматривается цепь Маркова переменного
порядка (ЦМПП). Построены статистические
оценки параметров модели, найдены необходимые
и достаточные условия эргодичности. Разработан
тест на основе частотных статистик ЦМПП для
выявления
зависимости
в
выходной
последовательности
криптографического
генератора.
2 ВВЕДЕНИЕ
Важной задачей в защите информации является
выявление
зависимостей
в
выходных
последовательностях
криптографических
генераторов [1]. Похожие задачи статистического
анализа временных рядов часто встречаются в
кибернетике [2], генетике [3], экономике [4],
социологии, медицине и во многих других областях
научной
и
практической
деятельности.
Для
моделирования
дискретных
временных
рядов
применяются цепи Маркова. Наиболее общей моделью
является цепь Маркова s -го порядка [5]. Однако число
параметров D  ( N  1) N данной модели возрастает
экспоненциально при увеличении порядка. Для
статистического оценивания параметров требуется
иметь реализацию не всегда доступной на практике
длительности.
Поэтому
построен
ряд
«малопараметрических» моделей цепи Маркова
высокого порядка [6-8], одной из которых является
цепь Маркова переменного порядка.
s
3 ЦМПП(S) И ЕЕ ВЕРОЯТНОСТНЫЕ СВОЙСТВА
Пусть A  0, 1, , N  1 – пространство состояний
мощности 2  N   , x1k  ( x1 ,, xk ), x1k  Ak –
(строка)
из
k
с числом элементов | xij | j  i  1, 1  i, j  k , i  j ,
uw  (u1 , u2 ,, u u , w1 , w2 ,, w w )
строк u, w ,
 X t  AtZ
–
конкатенация
– однородная цепь Маркова s-
го порядка, заданная на вероятностном пространстве
, F ,  , с матрицей вероятностей одношаговых
переходов P  ( p x s , x ) ,
s 1
1
Ключевые
слова
контекстная
функция,
равномерно
распределенная
случайная
последовательность, цепь Маркова переменного
порядка, частотные статистики.
символов
элементов, xij  ( xi , xi 1 ,, x j ) – фрагмент строки x1k
pxs , x
1
s1
 P{X t 1  xs 1 X t  xs ,, X t  s 1  x1} ,
где x1s 1  As 1 .
Определение
1
[6].
Цепь
 X t tZ
Маркова
называется цепью Маркова переменного порядка
ЦМПП( s ), если еѐ вероятности одношаговых
переходов p x s 1 имеют вид:
1
p xs , x
1
0  qxs
 
s l 1 , xs 1
s 1
 q xs
s l 1 , xs 1
,
(1)
 
 1, l  l x1s , x1s 1  As 1 , l  0, 1,, s,
l x1s  mink : P{X t 1  xs 1 X t  xs , X t s 1  x1} 
 P{X t 1  xs1 X t  xs ,, X t k 1  xsk 1}.
Соотношение (1) означает, что вероятность перехода
в состояние x s 1 зависит не от всех s предыдущих
  состояний. Помимо l 
контекстная функция cx   x
состояний, а лишь от l x1s
s
1
в
s
s l 1 ,
[6] определена
которая цепочке предыдущих состояний ставит в
соответствие цепочку из l значимых состояний –
 
контекст [6]. Если l x1s  s , то получаем полносвязную
 
цепь Маркова s-го порядка; если x1s  As , l x1s  0 , то
имеем последовательность независимых случайных
величин. Через τ обозначим множество значений
функции c .
Функция l  обладает следующим свойством: если
 
l x1s  l0 , l0  1,2,, s,
y1s l0 1  As l0 1 .
то


l y1s l0 1 xssl0  2  l0 ,
ВЕРОЯТНОСТНО-СТАТИСТИЧЕСКИЕ СВОЙСТВА ЦЕПЕЙ МАРКОВА ПЕРЕМЕННОГО ПОРЯДКА
Доказательство.

Предположим,
l ( y1s l0 1 xssl0  2 )
y1s l0 1  As l0 1 ,
 l1  l0 .
определения контекстной функции имеем:

 PX
что

Из
P X s 1  xs 1 X s  xs ,, X s l0 1  0   
s 1

 xs 1 X s  xs ,, X s l0 1  N  1 ,
 
что противоречит тому, что l x1s  l 0 .
Контекстную функцию c и функцию l  удобно
представлять в виде корневого дерева, которое
называется контекстным деревом. У каждой вершины
в таком дереве может быть не более N потомков,
поскольку каждому узлу (кроме корня) соответствует
элемент из пространства состояний A . Каждому
значению контекстной функции соответствует ветвь
контекстного дерева. Заметим, что если у каждой
вершины контекстного дерева, не являющейся листом,
имеется ровно N потомков, то такое контекстное
дерево соответствует полносвязной цепи Маркова s-го
порядка. Такое контекстное дерево называется
максимальным контекстным деревом.
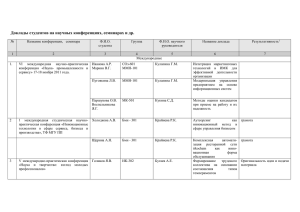
Пример 1. Пространство состояний A  0, 1,
порядок
s  3 , контекстная функция
c и
соответствующее ей контекстное дерево имеют вид:
0, x3  0, x2 , x1  A;

0, 1, x3  1, x2  0, x1  A;
c( x13 )  
0, 1, 1, x3  1, x2  1, x1  0;
1, 1, 1, x3  1, x2  1, x1  1.
Xt
0
x3
1
0
x2
1
с расширенным пространством состояний и используя
необходимое и достаточное условие эргодичности для
цепи Маркова первого порядка X (t ,s ) [9], приходим к
требуемому результату.
Обозначим  x s  PX 1  x1 ,, X s  xs , x1s  A s , –
1
начальное s -мерное распределение вероятностей
ЦМПП( s ).
Лемма 1. Распределение вероятностей реализации
X   X 1 , X n  ЦМПП s  имеет вид:
PX 1  x1 ,, X n  xn    x s 
1
x1
1
Рис.1. Контекстное дерево
Найдем условия, при которых ЦМПП s 
эргодической.
Теорема 1. Цепь Маркова переменного
ЦМПП s  с контекстной функцией c
эргодической тогда и только тогда, когда
такое m  s, m  N , что
m
min
m s
x1s , xm1 As
  pc ( x
xsm1Ams i 1
i  s 1
), xi s
i
0.
Доказательство. Переходя от ЦМПП s  к цепи
Маркова первого порядка X (t , s )   X t ,, X t  s 1 , t  Z ,
i 1
is
.
i
4 ОЦЕНИВАНИЕ ПАРАМЕТРОВ МОДЕЛИ
Оценки для переходных вероятностей ЦМПП s  ,
предложенные в [6], имеют вид:
qˆ x s
s  l 1 , xs 1

ν x s 1 (n)
s  l 1
ν xs
s  l 1
ν x b ( n) 
где
( n)
,
(2)
n b  a
δ X
a
i 1
ЦМПП s  , δ x k , y k 
1
1
– частотные статистики
i b  a b
, xa
i
k
δ x ,y , δ x ,y
i
i 1
i
i
i
– символ Кронекера.
Покажем, что приведенные оценки являются
условными оценками максимального правдоподобия.
Теорема 2. Если для реализации X   X 1 , X n 
ЦМПП s  , определяемой (1), длительности n  s с
выполнено условие
c
(n)  0 , то оценки (2) являются условными
известной
ν xs
функцией
оценками максимального правдоподобия.
Доказательство. Используя результат леммы 1,
построим логарифмическую функцию правдоподобия:


ln X , qω,u ωτ,uA  ln  x s 
является
порядка
является
найдется
n
 qcx ,x
i  s 1
Доказательство. Используя формулу умножения
вероятностей и марковское свойство, приходим к
требуемому результату.
s l 1
0
2
 ln  x s 
1
1
n
 ln qcx , x
i  s 1
i 1
i s

i
 ωu nln qω,u .
uA,
ωτ
Экстремальная задача для нахождения оценок
максимального правдоподобия имеет вид:
l n X , qω,u 
 ln  x s   ωu n  ln qω,u  max,
ωτ ,uA
1

qω,u
uA,

uA,ωτ
ωτ

 qω,u  1, ω  τ.
uA




ВЕРОЯТНОСТНО-СТАТИСТИЧЕСКИЕ СВОЙСТВА ЦЕПЕЙ МАРКОВА ПЕРЕМЕННОГО ПОРЯДКА
Используя метод множителей Лагранжа для решения
данной задачи, приходим к оценкам (2).
Рассмотрим
стационарную
цепь
Маркова
переменного порядка. Тогда оценки (2) являются
несмещенными и состоятельными.
Пусть  X t  AtZ – ЦМПП (s ) , определяемая (1),
2  l  s , – ветвь контекстного дерева. Построим
алгоритм оценивания контекстного дерева для
ЦМПП (s ) , основанный на проверке следующих
вспомогательных гипотез о значимости символов: H 0
x1l ,
– первый символ x1 в цепочке x1l не является
значимым, то есть
PX l 1  xl 1 X l  xl ,, X 1  x1 
 PX l 1  xl 1 X l  xl , , X 2  x 2 ; H 1 – вся цепочка x1
5 ПРОВЕРКА ГИПОТЕЗ О ЗНАЧЕНИИ
ПАРАМЕТРОВ ЦМПП

1
l 1
1
1
l 1
Теорема 3. Если справедлива гипотеза H 0 , то при
n   распределение статистики γ(n) сходится к χ 2 распределению с N  1 степенью свободы.
Доказательство. Воспользовавшись тестом для
проверки гипотезы о порядке цепи Маркова [10],
получаем требуемый результат.
Теорема 3 позволяет построить тест, основанный на
статистике γn  :
– ЦМПП (s ) , определяемая (1).
Построим тест для проверки гипотез: H 0 :  X t  AtZ
–
равномерно
распределенная
случайная
последовательность
[1],
то
есть
случайная
последовательность, элементы которой независимы в
совокупности и имеют равномерное распределение
вероятностей q x s , x  1 / N ; H1 :  X t  AtZ – цепь
s l 1
s 1
Маркова переменного порядка с переходными
вероятностями одношаговых переходов
q xs
s l 1 , xs 1

 q xs
s l 1 , xs 1
n 
1  ω xssl11 n  
1
 0, где ω x s1 n  n
 ω x s1 ,

s l 1
s l 1
N 
n 

причем
xs 1A

ω x s 1  0,
s l 1
xssl11Al
(5)
ω x s 1  0.
s l 1
Асимптотическое соотношение (5) означает, что
рассматривается
контигуальное
семейство
альтернатив.
Введем в рассмотрение следующие случайные
величины:
ν (n)  n / N l 1
, i  i1l 1  Al 1 ,
ξ i ( n)  i
l 1
n/ N
2
 H 0 : γ ( n )  Δ,

 H 1 : γ ( n )  Δ,
(4)
ρ( n) 
N
  ξ (i ,,i
2
1
k,
ilk 1 1
(i1 ,,ilk )τ
где Δ – порог, определяемый из заданного уровня
значимости α .
Следствие 1. Пусть α  0, 1 и Δ
1 α
квантиль
уровня
 X t  AtZ
Пусть
l
является значимой. Введем в рассмотрение статистику:
( ν x l 1 (n)  ν x l (n) pˆ x l , x ) 2
1
1
1 l 1
γ ( n) 
.
ˆ
ν
(
n
)
p
x , x A
xl
xl , x
3
 GN11
1  α
–
стандартного
χ  распределения с N  1 степенью свободы. Тогда
при n   размер теста равен α .
Доказательство. Найдем порог  , при заданном
уровне значимости α :
α  PH 1 H 0   Pγ̂(n)   H 0   1  Pγ̂(n)   H 0  
2
1  G N 1 () ,
  GN11 (1   ) , откуда и следует
требуемый результат.
Численные результаты, полученные в результате
компьютерного моделирования, показывают, что
алгоритм
оценивания
контекстного
дерева,
основанный на проверке вспомогательных гипотез о
значимости символов является более точным, чем
контекстный алгоритм, предложенный в [6] при малых
длинах n n  10000 реализации ЦМПП.
lk 1 )

( n) 
k,
(i1 ,,ilk
 N


 .
ξ
(
n
)
(i1 ,,ilk 1 )


ilk 1 1


)τ

Теорема 4. Если справедлива гипотеза H 0 , то при
n   распределение вероятностей статистики ρ(n)
сходится
к
χ 2 -распределению
M  τ ( N  1)
с
степенями свободы. Если справедлива гипотеза H1 , то
при n   распределение статистики ρ(n) сходится к
нецентральному χ 2 -распределению с M степенями
свободы и параметром нецентральности
определяемому следующей формулой:
2
1
a2 
 ω x1xlk ,xlk 1 .
Nτ
k,

a2 ,

( x1 ,xlk )τ
Доказательство. Воспользовавшись теоремой 2 из
[11] и применив линейное преобразование статистики
ρn  , получаем требуемый результат.
С помощью теоремы 4 построим тест, основанный
на статистике ρn  :
ВЕРОЯТНОСТНО-СТАТИСТИЧЕСКИЕ СВОЙСТВА ЦЕПЕЙ МАРКОВА ПЕРЕМЕННОГО ПОРЯДКА
 H 0 : ρ ( n )  Δ,

 H 1 : ρ ( n )  Δ,
где Δ – порог, определяемый из заданного уровня
значимости α .
Следствие 2. Пусть α  0, 1 и   GN1τ 1  α  –
квантиль
уровня
χ  распределения
2
с
стандартного
1 α
степенями
U  N  1 τ
свободы. Тогда при n   размер теста равен α .
Доказательство аналогично следствию 1.
Следствие 3. Мощность теста w при n  
удовлетворяет
следующему
асимптотическому
соотношению:
w 
1  GU ,a GU1 1    ,
n

где
GU ,a 
–
функция

нецентрального
2-
распределения с U степенями свободы и параметром
нецентральности a .
Доказательство. Используя определение мощности
и результат следствия 2 имеем:
w  1  PH 0 H1  1  P n   H1n





1  GU ,a    1  GU ,a GU1 1    .
n
Результаты
компьютерных
экспериментов
показывают, что значение мощности построенного
теста w и его оценки превышают соответствующие
значения для аналогичного теста из [11], что
свидетельствует о более высокой эффективности теста,
построенного на основе статистики  n  .
Отметим, что при увеличении длины реализации
ЦМПП не наблюдается сходимости мощности теста к
единице, поскольку рассматривается контигуальное
семейство альтернатив, то есть при увеличении
длительности n наблюдаемой последовательности,
гипотеза
сближается с гипотезой
H0
H1 :
H 1 
 H 0 .
n
ЛИТЕРАТУРА
[1] Математические
и
компьютерные
основы
криптологии / Ю.С. Харин [и др.]. – Минск. :
Новое знание, 2003. – 381 с.
[2] Медведев,
Г.А.
Вероятностные
методы
исследования экстремальных систем / Г.А.
Медведев. – М. : Наука, 1967. – 380 с.
[3] Уотермен, М.С. Математические методы для
анализа последовательностей ДНК / М.С.
Уотермен. – М. : Мир, 1999. – 350 с.
[4] Ching, W. K. High-order Markov chain models for
categorical data sequences / W. K. Ching, E. S. Fung,
K. N. Michael // Wiley Periodicals. Inc. Naval
Research Logistics. – 2004. – Vol. 51. – P. 557 – 574.
4
[5] Кемени, Дж. Конечные цепи Маркова / Дж.
Кемени, Дж. Снелл. – М. : Наука, 1970. – 272 с.
[6] Buhlmann, P. Variable length Markov chains / P.
Buhlmann, A. Wyner // The Annals of Statistics. –
1999. – Vol. 27, № 2. – P. 480-513.
[7] Харин, Ю.С. Цепь Маркова с частичными связями
ЦМ( s, r ) и статистические выводы о ее
параметрах / Ю.С. Харин, А.И. Петлицкий //
Дискретная математика. – 2007. – Т. 19, № 2. – С.
109-130.
[8] Raftery, A.E. A model for High-Order Markov Chains
/ A. E. Raftery // J. Royal Statistical Society. – 1985. –
Vol. B-47, № 3. – P. 528–539.
[9] Дуб, Дж. Вероятностные процессы / Дж. Дуб. – М.,
1956. – 605 с.
[10] Basawa, I.V. Statistical inference for stochastic
processes / I. V. Basawa. – AP, 1980. – 435 p.
[11] Тихомирова, М. И. О двух статистиках типа хиквадрат, построенных по частотам цепочек
состояний сложной цепи Маркова / М. И.
Тихомирова, В. П. Чистяков // Дискретная
математика. – 2003. – Т. 15, №2. – С. 149 – 159.