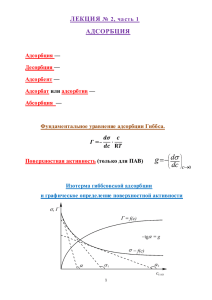
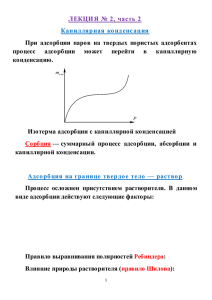
И адсорбция газа на твердой поверхности
реклама

Федеральное агентство по образованию Российской Федерации Московская государственная академия тонкой химической технологии им. М. В. Ломоносова Кафедра коллоидной химии И. А. Туторский ВВЕДЕНИЕ В КОЛЛОИДНУЮ ХИМИЮ. ЧАСТЬ 1. ПОВЕРХНОСТНЫЕ ЯВЛЕНИЯ И АДСОРБЦИЯ ГАЗА НА ТВЕРДОЙ ПОВЕРХНОСТИ. (главы 1,2,3,4) Учебное пособие Москва 2007 ББК 23.9 УДК 541.183 И. А. Туторский Поверхностные явления и адсорбция газа на твердой поверхности Учебное пособие М., МИТХТ им. М. В. Ломоносова, 2007 – 87 с. Данное учебное пособие соответствует программе лекционных курсов “Коллоидная химия” и “Поверхностные явления и дисперсные системы” для студентов 3 и 4 курсов для направления бакалавриата 510500 “Химия” и 550800 “Химическая технология и биотехнология” очной формы обучения. В нем излагаются основы термодинамики поверхностного слоя и закономерности адсорбции на твердой поверхности. Утверждено Библиотечно-издательской качестве учебного пособия. комиссией МИТХТ в Учебное пособие © МИТХТ им. М. В. Ломоносова, 2007 2 И. А. Туторский 87 1. Введение Содержание. 1. Введение................................................................................................. 3 1.1. Место коллоидной химии в общей системе наук .............................. 3 1.2. Краткие исторические сведения ......................................................... 5 1.3. Предмет коллоидной химии ................................................................ 6 1.4. Физические и химические поверхностные явления .......................... 9 1.5. Основные признаки объектов коллоидной химии ........................... 13 1.6. Фундаментальные особенности ультрадисперсного (коллоидного) состояния вещества.................................................................................. 19 1.7. Влияние дисперсности на свойства вещества ................................ 22 1.8. Значение коллоидной химии в природе и технике ......................... 24 2. Поверхностные явления и адсорбция ........................................... 32 2.1. Классификация поверхностных явлений ......................................... 32 2.2. Основы термодинамики поверхностного слоя ................................ 34 2.3. Интенсивные свойства гетерогенных систем.................................. 37 2.4. Экстенсивные свойства гетерогенных систем ................................ 40 2.5. Метод избыточных величин Гиббса ................................................. 41 2.6. Фундаментальное уравнение Гиббса для свободной энергии гетерогенной системы с плоской границей раздела фаз ...................... 44 2.7. Уравнение Гиббса для плоского поверхностного слоя .................. 46 3. Общие закономерности адсорбции ................................................ 50 3.1. Понятие об адсорбции....................................................................... 50 3.2 Количественные характеристики адсорбции ................................... 51 3.3. Типы адсорбционных зависимостей ................................................ 51 3.4. Адсорбция как обратимый экзотермический процесс .................... 53 3.5. Физическая адсорбция и хемосорбция ............................................ 56 3.6. Значение координационных связей при хемосорбции ................... 64 3.7. Природа адсорбционных сил ............................................................ 65 3.8. Изотермы адсорбции ......................................................................... 68 3.9. Кинетика адсорбции .......................................................................... 74 4. Адсорбция газов и паров на твердой поверхности..................... 75 4.1. Теория мономолекулярной адсорбции Ленгмюра .......................... 75 4.2.Полимолекулярная (потенциальная) теория адсорбции Поляни. . 80 4.3. Теория Брунауэра, Эммета и Теллера (БЭТ) ................................. 82 1.1. Место коллоидной химии в общей системе наук Коллоидная химия является фундаментальной наукой, возникшей в 60-х годах 19 века как самостоятельный раздел физической химии. Она занимает важное место в общей системе наук, которых в настоящее время насчитывается свыше 2,5 тысяч. Непрерывно продолжается процесс дифференциации и интеграции наук, в котором принимает участие и коллоидная химия. Дифференциация и интеграция в коллоидной химии составляют динамическое единство, обеспечивая взаимопроникновение различных наук, взаимное обогащение их теориями и методами. Выделившись из физической химии, коллоидная химия в свою очередь, отпочковала от себя такие науки, как химия полимеров, учение об аэрозолях, мембранология. Особо химия поверхностно-активных следует отметить тесную веществ, связь и взаимопроникновение коллоидной химии и нанохимии. Формирование нанотехнологии как нового крупного направления научно-технического прогресса потребовало рассмотрения в курсе коллоидной химии фундаментальных вещества, особенностей включая ультрадисперсного структурные, состояния термодинамические и квантовохимические эффекты. Развившись, новые науки обогатили коллоидную химию новыми методами и представлениями, коллоидная химия вобрала в себя достижения этих наук. Поэтому в настоящее время говорят о ренессансе коллоидной химии. Коллоидная химия имеет ярко выраженный пограничный характер и развивается в тесной связи с физикой, биологией, медициной, 86 3 химической технологией. Коллоидная химия входит в состав 1 фундаментальных, базовых естественных наук. Фундаментальность коллоидной химии как науки состоит в обширности изучаемых ею объектов и явлений, в широком применении химической термодинамики и статистики, и в том, что она связана с основными проблемами естествознания. Возьмем, например, одну из основных биологических проблем - проблему происхождения жизни. Д. Бернал считал, что расшифровать проблему происхождения жизни на Земле можно на основе адсорбции на различных сорбентах. Адсорбция является одним из основных разделов коллоидной химии. Академик Опарин придерживался p 1 pi 1 C 1 p ps max C p p s | p ps (4.9) и почленно делят числитель на знаменатель p pi 1 p C max 1 p s tg C 1 p p max C C 1 max C s (4.10) (4.11) мнения, что живые организмы на земле возникли вследствие коацервации, т. е. слияния мельчайших частиц живой материи. Живая клетка образуется и существует по законам коллоидной химии. В настоящее время наука о происхождении жизни переживает подъем, связанный с достижениями химии, физики и биологии. Какие бы гипотезы происхождения жизни ни выдвигались, суть их одна: биоорганический мир сформировался на основе предбиологических частиц и структур, имеющих коллоидный характер. Многие жизненные Рис. 4.7. процессы развиваются в био-гетерогенных системах. Геология также тесно связана с коллоидной химией. Земля Так графически находят значения констант С и max. является сложной дисперсной системой, в земной коре протекают разнообразные поверхностные явления. Геологические явления рассматриваются с позиций совместного действия механических, физических и химических сил. Многие горные породы являются дисперсными системами. Причины землетрясений также связаны с поверхностными явлениями. Коллоидная химия является теоретической основой изучения дисперсных систем в живой 4 природе, горных породах, 85 где max - емкость монослоя, pi - давление насыщенного пара при данной температуре. Уравнение (4.6) описывает всю изотерму полимолекулярной адсорбции (рис. 4.6). конструкционных материалах, к которым относятся резины и пластмассы. Коллоидная химия служит также обоснованием многих технологических процессов, таких как дробление, смешение, флотация, переработка полимеров. Являясь химией реальных тел, коллоидная химия завершает цикл химических дисциплин объединяет все в химико-технологических химические дисциплины, так как вузах. изучает Она как органические, так и неорганические объекты, использует различные физико-химические методы. 1.2. Краткие исторические сведения Среди химических наук коллоидная химия является сравнительно молодой, хотя коллоиды или коллоидные системы существуют Рис. 4.6. Изотерма полимолекулярной адсорбции. извечно. Однако, изучение коллоидных систем началось только в XIX При p p pi <<1 и C 1 , 1 pi 1 и уравнение (4.6) переходит в веке. Понятие о коллоидах возникло в 60-х годах XIX века, когда неорганическая, органическая и физическая химия были уже сформировавшимися науками. В частности, в 1861 году Бутлеровым уравнение Ленгмюра: была создана теория строения органических соединений. max C p p 1 C p В 1845 году итальянский химик Франческо Сельми, работавший в s (4.7) старейшем университете Европы города Болонья, получил растворы, обладающие особыми свойствами. Он обнаружил, что в этих ps По теории БЭТ легко найти удельную поверхность адсорбента растворах медленно протекает диффузия, они не проходят сквозь s уд max N a s 0 , где s 0 - площадь, занимаемая одной молекулой тонкие пергаментные фильтры, сходящийся пучок света образует адсорбата. добавление электролита) вызывают образование осадка, которое Для решения уравнения БЭТ его приводят к линейной форме: 1 p 1 C 1 p pi ps p | : 1 ps max C p p s 1 84 в них светящийся конус. Малейшие воздействия (перемешивание, протекает без выделения заметных количеств тепла и без изменения объема системы. Это свидетельствует об отсутствии химической (4.8) реакции. Сельми назвал эти растворы золями. Он получил золи серы, сернистого мышьяка, хлористого серебра. 5 Фарадей разработал методы получения золей благородных В отличие от теории Ленгмюра, в теории БЭТ адсорбция металлов - золота и серебра. Полученные Фарадеем свыше 100 лет рассматривается как многослойная, и допускается, что молекулы назад золи золота и серебра до сих пор хранятся в Лондонском музее. адсорбата на поверхности взаимодействуют с молекулами адсорбата Название «коллоиды» было предложено английским ученым Т. в объеме. Это справедливо при адсорбции паров, когда энергия Грэмом в 1861 году и происходит от греческого слова «колла» () межмолекулярного взаимодействия сопоставима с энергией теплового органического движения молекул. В теории БЭТ принимается, что состояние молекул концентрации во втором и последующих слоях подобно жидкости и отличается от i - студневидные растворы с клеящими свойствами. К ним относятся го слоя. Теплота адсорбции первого слоя есть теплота адсорбции желатин, крахмал, клей. Qад , а теплоты адсорбции всех последующих слоев одинаковы и - клей. Грэм происхождения, исследовал образующие в основном при золи некоторой Становление коллоидной химии как области знания произошло тогда, когда физики и химики обратили внимание на особые свойства равны теплоте объемной конденсации L Qад . Полимолекулярная поверхности раздробленных, т.е. дисперсных тел. Поверхность, ранее адсорбция рассматривается как протекание множества химических считавшаяся лишь внешней частью предмета или тела, в науке о реакций. коллоидах предстала в виде площади, заселенной открытыми атомами. 1.3. Предмет коллоидной химии Физическая химия интересуется преимущественно объемными свойствами фаз и изучает в основном индивидуальные вещества или истинные растворы, которые являются гомогенными системами. Можно показать, что в этом адсорбции выражается уравнением: Qa L K' C g ' e RT KL Двухфазные системы, изучаемые физической химией, состоят из фаз большой протяженности, в которых значение поверхности невелико. Коллоидная химия изучает поверхностные явления и гетерогенные случае константа равновесия где (4.5) K ' - константа равновесия образования единичного высокодисперсные системы. Они занимают промежуточное положение адсорбционного комплекса, KL - константа равновесия образования между грубыми дисперсиями и истинными растворами. Если одно всех последующих комплексов, Qa L - чистая теплота адсорбции. вещество диспергировано в другом в виде частиц, можно выделить три типа систем, размер которых убывает в ряду: грубодисперсные > микрогетерогенные > ультрадисперсные (коллоидные). Эти системы по меньшей мере двухфазны. Напомним, что фаза - совокупность 6 Уравнение изотермы адсорбции в теории БЭТ имеет вид: 1 p max C p p s ps 1 C 1 p ps 83 (4.6) a2 , a3 ... an . При T Tкр весь адсорбционный объем занят жидкостью, т. е. V a свойствам и отделенная от других частей системы поверхностью . Адсорбционный потенциал - это работа объема, где давление p к объему, в котором газ конденсируется. В i , находящейся на поверхности раздела жидкость - газ в pi значений р и строят характеристическую кривую. адсорбента Поляни и применима в котором Межфазный слой осуществляется всегда межфазное уменьшает разность сил. Поверхностный и межфазный слой фазовые переходы и термодинамические функции. Понятие о поверхностном или межфазном слое введено в науку Гиббсом. Фаза, состоящая из отдельных частиц, называется дисперсной фазой. Она прерывиста, дискретна. Другая фаза, в которой распределены частицы, называется дисперсионной средой. Она Теории Ленгмюра и Поляни ограничены и применяются в Теория слое, сосуществуют с объемными фазами, имеют свою фазовую диаграмму, RT pV RT ; V ; Определяют значения Vi и i для разных p адсорбции. поверхностном межмолекулярных (4.4) где pi - давление насыщенного пара над поверхностью жидкости. природы Правильнее говорить не о геометрической поверхности, а о энергии фаз. Толщина этого слоя определяется радиусом действия pi pi dp i Vdp RT RT ln p p p p от распределенных в какой-либо среде, то такая система двухфазна. взаимодействие. адсорбционном объеме pi . зависимости раздела. Отметим, что коллоидная частица – это не фаза, а фазовая частица. Если система содержит множество частиц одного сорта, сжатия одного моля газа при температуре T или работа перехода от точке частей системы, одинаковых по составу, физическим и химическим адсорбата и только физической к условий адсорбции. Теория Ленгмюра применима как к физической, так и к химической адсорбции, но неприменима к адсорбции тонкопористыми сорбентами. 4.3. Теория Брунауэра, Эммета и Теллера (БЭТ) Эта теория является обобщением теорий Ленгмюра и Поляни. В ней сделана попытка описать изотермы моно- и полимолекулярной адсорбции с помощью одного уравнения. В основе этой теории в основном лежат те же положения, что и в основе теории Ленгмюра, т.е. на поверхности адсорбента имеются активные центры, и взаимодействием между молекулами адсорбата в слое пренебрегают. 82 является непрерывной, сплошной. Коллоидная химия изучает особые, ультрадисперсные, т. е. сильно раздробленные вещества. Коллоидная химия имеет дело главным образом не с молекулами, а с их агрегатами. Коллоидная химия - это наука о поверхностных явлениях и гетерогенных дисперсных системах. Две части этого определения, т.е. поверхностные явления и дисперсные системы, тесно связаны между собой. Рассмотрим причины этой взаимосвязи. Объектами коллоидной химии могут быть тела любой величины, однако поверхностные явления проявляются сильнее всего в высокодисперсных системах: пленках, нитях, капиллярах, мелких частицах. В этих системах наиболее ярко проявляется все многообразие поверхностных явлений. Это происходит оттого, что с 7 увеличением раздробленности вещества возрастает доля молекул, Характеристикой силового поля является адсорбционный молекул, потенциал , представляющий собой работу перемещения одного находящихся на поверхности частицы кубической формы f, от длины моля адсорбата из адсорбционного объема в газовую фазу. Эта ребра куба l, проходит через максимум, расположенный при 10-9м (рис. работа совершается против адсорбционных сил. находящихся на поверхности. Зависимость доли -6 1.1). Для частицы с длиной ребра l=10 м, на котором помещается 5000 молекул, доля молекул, находящихся на Силовое поле сходно с гравитационным в том отношении, что оно поверхности, ненасыщаемо и силы не зависят от температуры. Параллельно составляет всего 0,1%, а для частицы с l=210 м (на ребре 10 поверхности адсорбента проводятся поверхности с одинаковыми молекул), доля этих молекул составляет 50%. Частицы таких размеров значениями потенциала, т.е. эквипотенциальные поверхности со содержат поверхности, значением потенциалов 1 , 2 , 3 . Кривая f () , где - становится расстояние от поверхности адсорбента или f (V ) называется -9 около следовательно, половины всех поверхность даже молекул на количественно полноправным партнером объемной фазы и значение поверхностных явлений для систем, содержащих такие частицы, очень велико. характеристической адсорбционного кривой. объема, т.к. Удобнее его пользоваться можно найти значением из опыта. Характеристическая кривая характеризует каждую пару адсорбент адсорбат и не зависит от температуры. Согласно теории Поляни, болеее активны впадины, т.к. в них происходит сгущение силовых линий. Рис. 1.1. Зависимость доли молекул, находящихся на поверхности куба, от длины ребра. Величина поверхности в реальных сильно раздробленных системах, к которым относятся все композиционные материалы, очень велика. Так, в небольшом объеме армированного волокном пластика, величиной V=16,4см3, содержащего 50 объемных % волокна d=7,6мкм, поверхность раздела между волокном и связующим равна 41936см2. Рис. 4.5. Характеристическая кривая адсорбции Уравнение изотермы адсорбции в теории Поляни не выводится. Путь построения характеристической кривой состоит в том, что при определенных значениях p1 , p2 , p3 ... pn определяют значения a1 , 8 81 конденсацией. Изотермы адсорбции полимеров, как правило, не являются ленгмюровскими, т. к. одна макромолекула занимает несколько активных центров адсорбента, т. е. предпосылки, положенные в основу уравнения Ленгмюра, не соблюдаются. 1. Адсорбционные силы являются физическими, адсорбция нелокализована. 2. Активных центров на поверхности адсорбента нет. Над поверхностью адсорбента действует непрерывное поле межмолекулярных сил, потенциал которого убывает по мере удаления от поверхности. 3. Адсорбированные молекулы не препятствуют адсорбции полимолекулярная адсорбция, явления на поверхности капли или пузырька, изотермическая перегонка, смачивание, коалесценция, коагуляция, а в В основу этой теории положены следующие исходные положения: слоев, иметь физическую и химическую природу. капиллярные адсорбции Поляни. молекулярных Поверхностные явления чрезвычайно распространены и могут К физическим поверхностным явлениям и процессам относятся 4.2.Полимолекулярная (потенциальная) теория последующих 1.4. Физические и химические поверхностные явления т. е. адсорбционный идет объем заполнен многими молекулами. твердых телах - когезия, адгезия, трение. В качестве примера физического поверхностного явления можно привести существование капиллярного давления на поверхности капли или пузырька, вызванного кривизной поверхности. Поверхность жидкости состоит из молекул, находящихся в несимметричном силовом поле. Притяжение со стороны жидкости не компенсируется притяжением со стороны менее плотной фазы - пара. Равнодействующая межмолекулярных сил, действующих на одну молекулу, не равна нулю и направлена в сторону более плотной фазы - жидкости (рис. 1.2). Равнодействующая всех сил, направленная нормально к поверхности и рассчитанная на 1м2, называется молекулярным или внутренним давлением, которое измеряется в Н/м2 или Дж/м3. Для полярных жидкостей внутреннее давление очень велико. Для воды оно превышает 1,1ГПа (гигапаскаля), что соответствует 11 тыс. атмосфер. Рис. 1.2. Межмолекулярные взаимодействия в конденсированной фазе. Рис. 4.4. Эквипотенциальные поверхности и адсорбционный объем. 80 9 Наличие кривизны приводит к изменению внутреннего давления. При вогнутой поверхности ((dsмол/dV)<0) внутреннее давление будет меньше, а при выпуклой ((dsмол/dV)>0) больше, чем в случае плоской поверхности. Величина p p p , равная разности давлений в '' соседних называется фазах, ' разделенных капиллярным искривленной давлением. По поверхностью, закону Лапласа p=(dsмол/dV). В зависимости от знака кривизны капиллярное давление может увеличивать или уменьшать внутреннее давление. По величине поднятия или опускания жидкости в капиллярах Рис.4.2. Решение уравнения Ленгмюра tg можно определять поверхностное натяжение жидкостей, которое рассчитывается по формуле Жюрена: 2 cos h r g (б е ) Уравнение (1.1) Ленгмюра позволяет 1 ; max max ctg определить удельную поверхность адсорбента. Действительно, произведение max N a , где Na - число Авогадро равно числу молекул, приходящихся на 1 см2 поверхности. Умножив это значение на площадь, занимаемую одной молекулой величину удельной поверхности s0 получим s уд max N a s 0 . Рис. 1.3. Капиллярное давление Капиллярное давление проявляется при сушке влажных дисперсных структур. У искривленной поверхности изменяется химический потенциал, что приводит к увеличению давления Рис. 4.3. Изотерма полимолекулярной адсорбции. насыщенного пара над выпуклой поверхностью жидкой капли и его уменьшению над вогнутой поверхностью. Изменение давления насыщенного пара описывается уравнением Томсона - (Кельвина): Часто изотермы имеют вид, отличающийся от ленгмюровской изотермы, а именно S -образный вид (Рис. 3.46). Это объясняется 10 адсорбции полимолекулярной адсорбцией, 79 или капиллярной ln Pr ln PS где 2 VM 2 VM ; ln Pr ln PS , r R T r R T (1.2) PS и Pr - давление насыщенного пара над ровной и искривленной поверхностью, V M - мольный объем жидкости. Величина 1/r характеризует кривизну поверхности сферической частицы. Чем больше кривизна, тем легче молекулы отрываются от поверхности и интенсивнее протекает испарение капель. Вследствие этого над мелкими каплями упругость пара больше, чем над крупными. Поэтому в атмосфере насыщенного пара мелкие капли переходят в Рис. 4.1. Решение уравнения Ленгмюра. По первому способу по изотерме находят значение продолжают начальный пересечения с линией перпендикуляр до точки прямолинейный max участок max . крупные Затем изотермы до и из точки пересечения опускают K max K p ' . При max K p' 1 . Отсюда 1 . p' Второй способ решения уравнения Ленгмюра применяется, когда росту max растворимости с увеличением ln C r ln C Изменение дисперсности, которое 2 VM r R T (1.3) Вследствие этого растворимость мелких твердых частиц больше, чем крупных. Происходит процесс растворения мелких частиц и рекристаллизации их переконденсация, называемая на крупных, то есть Оствальдовским изотермическая созреванием и описываемая уравнением: 1 1 2 VM C r1 C r2 r1 r2 R T неизвестно. Уравнение преобразуется в уравнение (1.4) При спекании металлических порошков происходит постепенная прямой: 1 перегонки. описывается уравнением Гиббса-Фрейндлиха-Оствальда: экспериментальная изотерма не имеет третьего линейного участка, т. е. значение изотермической химического потенциала вследствие кривизны поверхности приводит к p' на оси абсцисс. При малых p значение K p 1 , и им знаменателе можно пренебречь. Тогда уравнение принимает вид: вследствие 1 1 Kp 1 1 p p ; max Kp max Kp max max K max ликвидация (4.5) Над малой порой повышена концентрация микропустот (вакансий) в частицах. Это приводит к их диффузии от малых пор к большим и к поверхности раздела металла с воздухом. Под 78 пор. действием лапласовых сил 11 поры исчезают, заполняются K - константа адсорбционного металлом. Этот процесс сопровождается уменьшением поверхности слоя, т. е. емкость монослоя. раздела фаз. равновесия, связанная с теплотой адсорбции. Другими примерами физических поверхностных явлений являются смачивание и, как следствие этого, существование вогнутого и K характеризует энергию взаимодействия адсорбата с адсорбентом, т. е. химическое сродство. Для любой химической реакции справедливо выражение: выпуклого менисков жидкости и перемещение жидкости в капилляре. В G R T ln K ; G H T S ; дисперсных системах смачивание уменьшает взаимодействие частиц. H Q ; Если частицы имеют ультрамикроскопические размеры, то смачивание способствует образованию золей. Когда частица достаточно велика и оседает, смачивание способствует скольжению частиц друг K e G RT e H T S RT e S R e Q RT g e Q RT (4.3) относительно друга, приводя к более плотной упаковке осадка. Если смачивание неполное, то при взаимодействии частиц происходит преобразование пространственных структур (каркасов и рыхлых осадков). При смачивании процесс сопровождается изменением свойств поверхности. Поверхность твердое тело - газ заменяется поверхностью твердое тело - жидкость, поверхностное натяжение Рассмотрим насколько хорошо описывает уравнение Ленгмюра изотерму адсорбции на всех ее участках. На изотерме адсорбции, изображенной на рис. 3.40 можно выделить три участка. При малых значениях такое значение уменьшается. К Анализ уравнения Ленгмюра физическим поверхностным явлениям относятся также химических поверхностных явлений p , когда значение K p 1 , и уравнение Ленгмюра принимает вид: max K p образование и рост зародышей в растворе и диспергирование. Примерами p всегда можно выбрать являются адсорбция и коррозия. Тончайшие слои адсорбированного вещества изменяют свойства поверхности - ее смачивание, возможность То есть (4.4) пропорциональна p , что соответствует начальному линейному участку кривой. При больших значениях p можно p , когда величина K p 1 и max , взаимодействия с другими веществами. В коллоидных системах, подобрать такие значения обладающих большой поверхностью, роль адсорбции особенно что соответствует третьему участку изотермы. Второй криволинейный фазы участок изотермы описывается полным уравнением Ленгмюра. Таким диффундирует тот компонент, который уменьшает поверхностное образом, это уравнение хорошо описывает всю изотерму адсорбции, в натяжение. отличие от уравнения Фрейндлиха. велика. При адсорбции на поверхность из объемной Существует два способа графического Ленгмюра (рис 4.1). 12 77 решения уравнения поверхности не зависит от того, занят соседний активный явления протекают с уменьшением поверхности или поверхностного центр или нет. Ленгмюр рассматривал адсорбцию как квазихимическую реакцию между газом и активными центрами с образованием адсорбционного комплекса. 1.5. Основные признаки объектов коллоидной химии подробнее два основных признака объектов коллоидной химии: гетерогенность и дисперсность. Все свойства p , концентрацию свободных объектов коллоидной химии зависят от этих признаков. Эти признаки 0 , концентрацию занятых активных центров неотделимы друг от друга. Каждый из них является необходимым, но Обозначим давление газа через активных центров через натяжения. Рассмотрим молекула газа свободный активный центр адсорбционный комплекс p 0 через Рассмотрение этих примеров показывает, что все поверхностные . Тогда константа равновесия K p O недостаточным для отнесения системы к коллоидной. Так, истинные растворы дисперсны, но гомогенны, у них нет поверхности раздела, . поэтому они не изучаются в коллоидной химии. Гетерогенность или K p O ; O max ; K p max многофазность K p max k P ; K p K p max межфазной 1 Kp K p max ; является поверхности, признаком, обеспечивающим поверхностного слоя. Это наличие важнейший признак коллоидного состояния вещества, с ним связаны самые K p max 1 K p существенные свойства коллоидов. Гетерогенность указывает на (4.1) качественную сторону объектов коллоидной химии - наличие концентрации межфазной поверхности и качество этой поверхности. Поверхность адсорбата, т. е. количеству адсорбированного вещества а, т.к. один раздела представляет собой пример единства противоположностей. активный центр занимает одна молекула адсорбата. Молекулы Очевидно, a величина K p amax ; 1 K p выражения делят на Иногда равна поверхностной числитель и знаменатель этого на Существование поверхности межфазной принадлежат поверхности к обеим фазам. предполагает наличие поверхностного натяжения . Величина поверхностного натяжения определяет степень различия между соприкасающимися фазами. Чем K. a p amax p a max 1 A p p K сильнее выражена гетерогенность, т. е. чем более резко отличаются (4.2) Константы уравнения Ленгмюра имеют следующий смысл. фазы по своей природе, тем больше величина поверхностного натяжения. При отсутствии гетерогенности поверхностное натяжение max - это максимальная адсорбция при образовании мономолекулярного 76 равно 0. Характеризуя гетерогенность как признак коллоидных систем, связанный с поверхностью, необходимо отметить отличия молекул на 13 поверхности от молекул в объеме. Молекулы, находящиеся на поверхности, сильно отличаются от молекул, находящихся в объеме. Первое отличие состоит в том, что молекулы на поверхности находятся в ином энергетическом состоянии по сравнению с молекулами в объеме, т. е. обладают избыточной свободной энергией. 4. Адсорбция газов и паров на твердой поверхности 4.1. Теория мономолекулярной адсорбции Ленгмюра Молекулы в этом слое находятся в несимметричном силовом поле. Ленгмюр и Поляни одновременно в 1915 году разработали теории Молекулярные силы в поверхностном слое некомпенсированы, и адсорбции газов и паров на твердой поверхности. Эти теории поэтому молекулы на поверхности обладают избытком свободной являются ограниченными. Они применяются в зависимости от энергии Fs. Мерой этого избытка является поверхностное натяжение , природы адсорбента и адсорбата и условий адсорбции. Теория 1см2 Ленгмюра рассматривает физическую и химическую адсорбцию при величины поверхности s. Fs=sмол. Избыток свободной энергии на малом давлении и температуре ниже критической. Она неприменима к т.е. свободная поверхности поверхностная делает систему энергия, приходящаяся термодинамически на неравновесной. Поэтому все поверхностные процессы протекают самопроизвольно в сторону уменьшения Fs, что достигается уменьшением sмол или . Второе отличие состоит в том, что молекулы, находящиеся в объеме и на поверхности, по-разному ориентируются. Средняя конформация молекулы в объеме и на поверхности различна. Так, пленка стеариновой кислоты, отлитая на стекле, со стороны воздуха гидрофобна, а со стороны стекла гидрофильна. Суть третьего отличия состоит в том, что в кристаллических телах молекулы и атомы, находящиеся на поверхности, имеют иную электронную структуру по сравнению с молекулами и атомами расположенными в объеме. Четвертое отличие заключается в том, что в случае многокомпонентных систем состав поверхностного слоя и объема различен вследствие адсорбции. Дисперсность или раздробленность является количественным признаком объектов коллоидной химии. Применяются следующие количественные параметры раздробленности: размер частиц α, 14 тонкопористым сорбентам. Теория Поляни применима только к физической адсорбции. Теория Ленгмюра учитывает ограниченность поверхности адсорбента, что приводит к адсорбционному насыщению поверхности по мере увеличения концентрации адсорбата. При разработке этой теории Ленгмюром были сделаны следующие допущения: 1. Адсорбция локализована, адсорбционные силы близки к химическим. 2. Адсорбция происходит на активных центрах адсорбента, которые энергетически эквивалентны. 3. Радиус действия адсорбционных сил мал, и один активный центр адсорбирует одну молекулу адсорбата, причем образуется мономолекулярный адсорбционный слой. 4. Устанавливается динамическое равновесие адсорбция десорбция. 5. Между адсорбированными взаимодействие, вследствие 75 молекулами чего время отсутствует пребывания на дисперсность Д, удельная поверхность sуд. В зависимости от формы 3.9. Кинетика адсорбции Кинетика адсорбции подчиняется уравнению первого порядка, т.к. чаще всего лимитирующей стадией адсорбции является диффузия. Чем больше насыщение поверхности, т. е. меньше разность ( a at ), тем меньше скорость адсорбции. частицы берется ее характеристический размер: для сферы – диаметр d, для куба – ребро l. Для частиц неправильной формы в качестве количественной характеристики раздробленности применяются радиус эквивалентной сферы r и u. Между этими характеристиками существуют простые соотношения. da k a равн а d (3.12) С повышением температуры скорость адсорбции увеличивается, а равновесная адсорбция уменьшается (рис. 3.13) . Д 1 ; а 1 м (1.5) Для пористых или ячеистых тел, дисперсной фазой которых является газ, дисперсность выражается отношением числа атомов, находящихся на поверхности, ns, к общему числу атомов, n0: Ä ns n0 Удельная поверхность sуд - это отношение поверхности к объему или массе. При расчете удельной поверхности на единицу объема дисперсной фазы: Рис. 3. 13. Кинетические кривые адсорбции при различной температуре. Константа K зависит от теплоты адсорбции, температуры и коэффициента диффузии адсорбата. Температурный коэффициент адсорбции мал, т. к. энергия активации физической адсорбции равна 0. s óä s 12 ; V м2 1 3 , м м (1.6) Иногда удельную поверхность относят к единице массы: s óä s 12 ; V1 м2 кг (1.7) Для монодисперсной системы, содержащей n частиц сферической формы радиуса r : s óä 74 4 r 2 n 3 6 4 3 r n r d 3 15 (1.8) В общем случае s óä K , где K - коэффициент формы частицы. a показал, что при экспоненциальном распределении неоднородностей поверхности и среднем заполнении уравнение Фрейндлиха может быть получено теоретически. Для полидисперсной системы: s óä Я.Б.Зельдович Существует 5 основных типов изотерм адсорбции (рис. 3.12). 3ni ri 2 , ni ri3 (1.9) где ni - число частиц радиуса ri . Диспергирование можно производить уменьшением одного, двух или трех измерений (рис. 1.4). Рис. 3.12. Изотермы физической адсорбции. Рис. 1.4. Форма дисперсий, образующихся при изменении размеров куба в одном, двух или трех измерениях. Изотерма адсорбции 1 типа описывается уравнением Ленгмюра: В зависимости от этого образуются различные дисперсии: пленки, max k p (3.11) 1 k p нити или частицы. Раздробленность определяется наименьшим Этот тип изотермы соответствует мономолекулярной адсорбции. базовым размером a. Остальные типы изотерм соответствуют полимолекулярной Поверхностные явления возникают на любых поверхностях, независимо от их протяженности. Увеличение дисперсности приводит к увеличению роли поверхностных явлений в системе. Дисперсность термодинамическим или удельная параметром поверхность состояния, изменение адсорбции: 2 – S-образная кривая с линейным участком в области средних давлений; 3 – кривая, вогнутая к оси адсорбции без перегибов с монотонным увеличением является которого вызывает изменение других равновесных свойств. В качестве примера da ; 4, 5 – кривые типов 2, 3, dp осложненные капиллярной конденсацией, сопровождающей полимолекулярную адсорбцию. рассмотрим гетерогенную смесь воды с бензолом, содержащую 16 73 1 1, и а n небольшое количество поверхностно-активного вещества. В высоком 1 0 и a const . n смесь характеризуется определенным равновесным распределением изотермы. На начальном, линейном участке изотермы пропорциональна p . На третьем участке Следовательно, показатель степени 1 n характеризует кривизну характеризующая степень приближения изотермы к прямой. Чем 1 , тем круче криволинейный участок изотермы больше значение n Для определения констант ПАВ между поверхностью и объемом. Если эту смесь перелить в противень, то межфазная поверхность увеличится, количество ПАВ на криволинейного участка изотермы адсорбции. Это правильная дробь, адсорбции. узком цилиндре, где межфазная поверхность вода - бензол невелика, уравнения Фрейндлиха применяют логарифмирование. После логарифимирования уравнение 1 принимает вид lg a lg lg p . Из графической зависимости n поверхности увеличится, а концентрация в объеме уменьшится. Равновесие в системе изменится только за счет изменения дисперсности, или удельной поверхности при постоянстве других параметров (объема, массы, температуры, давления, числа компонентов). Это изменение является обратимым. Если пренебречь влиянием поверхности, то, согласно правилу фаз Гиббса F K Ф 2 , число степеней свободы F при постоянных температуре и давлении равно 1, т. е. можно изменять только количество ПАВ в системе. При постоянном содержании ПАВ F=0. С учетом влияния поверхности, т. е. дисперсности, появляется 1 . Отрезок, отсекаемый прямой линией на оси находят константы и n дополнительная степень свободы. Из приведенного примера следует, 1 (рис. 3.11). ординат, равен lg , а tg n ПАВ, т. е. система обладает дополнительной степенью свободы, и что изменение поверхности приводит к изменению распределения правило фаз записывается следующим образом: F K Ф 3 . Дисперсность характеризует количество поверхности, она является количественной характеристикой, указывающей на степень раздробленности, величину межфазной поверхности. Рис. 3.11. Решение уравнения Фрейндлиха. 72 17 Таблица 1.1. Дисперсность коллоидных систем Система Коллоидная а, м Таблица 3.1. Теплота и время прибывания молекулы на 1 Д, м электронный микроскоп и в атомный силовой Физическая адсорбция qa , кДж/моль (наноразмерная, ультрамикрогетерогенная), частицы видимы в поверхности для физической адсорбции и хемосорбции. 10 9 ÷ 10 7 10 9 ÷ 10 7 микроскоп Микрогетерогенная, частицы видны в обычный микроскоп Грубодисперсная, частицы видны невооруженным глазом 10 7 ÷ 10 5 10 5 10 7 ÷ 10 5 Хемосорбция ,с 1,6 1,110-12 60 210-2 6 1,310-12 80 1102 24 110-10 100 6105 40 310-6 120 4109 160 1017 808 10126 10 5 При qa , кДж/моль ,с адсорбции газов на гладкой поверхности равновесие характеризуются устанавливается очень быстро, в течение долей секунды. При широким диапазоном дисперсности, значения которой приведены в адсорбции на твердой пористой поверхности адсорбция замедляется табл.1.1. вследствие Системы, изучаемые в коллоидной химии, проникновения адсорбата в поры адсорбента, контролируемого диффузией. Зависимость удельной поверхности от размера частиц приведена Объединяя уравнения (3.7), (3.8) и (3.9), получим закон Генри: на рис. 1.5. Участок N p 0 exp( qa ) R T k P 2 M R T 2, соответствующий средним (3.10) давлениям является криволинейным, т.к. на этом участке достигается промежуточная степень заполнения поверхности адсорбента. Изотерма адсорбции имеет вид параболы и описывается 1 эмпирическим уравнением Фрейндлиха: a Рис. 1.5. Зависимость удельной поверхности от размера частиц. константы, не имеющие физического pn , смысла, где и но 1 n имеющие математический смысл. Эти константы не зависят от концентрации адсорбата. 18 Это уравнение хорошо 71 описывает среднюю часть При относительной влажности 10%, T 293 K , P 1,75 мм рт. ст. , Аналитически эта зависимость выражается формулой гиперболы. число молекул воды, сталкивающихся с поверхностью в секунду равно На этом графике существуют три области: 1 - истинные растворы молекулярной 10 21 . Площадь занимаемая молекулой воды на поверхности равна 10 Å2 , т. е. 10 что 15 см , следовательно, 1015 моль / см 2 . Это означает, 10 6 сек , а скорость установления равновесия крайне велика, степени дисперсности, 2 – высокодисперсные (наноразмерные, ультрадисперсные) системы с размером частиц 10-9 ÷ 10-7м, за которыми укрепилось название «золи», 3 - микрогетерогенные и грубодисперсные системы с размером частиц 107 ÷ 10-5 м. Эти системы представляют собой взвеси, которые со монослой образуется практически мгновенно. За время пребывания на временем оседают и образуют структуры в осадке. Размер частиц в поверхности молекулы адсорбата обмениваются тепловой энергией с них настолько велик, что частицы видны в обычный микроскоп или поверхностью адсорбента. Таким образом, без адсорбции теплообмен даже невооруженным глазом. Поскольку крупные частицы отражают был бы невозможен. Роль адсорбции в теплообмене составляет одно свет, эти системы обладают сильной мутностью. из важнейших ее проявлений в технических и природных процессах. Я.И.Френкель в 1924 году получил выражение для зависимости от T. oe 0 qa (3.9) 10 13 сек . Как видно из уравнения, сильно зависит от T и qa , т. к. они стоят в показателе степени. Ниже приведены значения , вычисленные для различных q a при комнатной температуре. Последнее значение ультрадисперсного (коллоидного) состояния вещества Ультрадисперсное RT - константа, равная периоду колебаний в решетке адсорбента порядка 1.6. Фундаментальные особенности больше возраста Земли и Солнечной системы. При qа 100 кДж / моль молекула живет на месте недели, годы или тысячелетия, поэтому хемосорбция в большинстве случаев является локализованной. состояние - это особый уровень состояния вещества, следующий за атомно-молекулярным уровнем, особое конденсированное состояние между молекулярным соединением и компактной массой материала. Отличия этого состояния настолько велики, что его называют пятым агрегатным состоянием вещества. Причина этих отличий в том, что число атомов на поверхности ультрадисперсной частицы (УДЧ) равно числу атомов в ее объеме n S n V , а свободная поверхностная энергия становится равной внутренней энергии частицы, т.е. Fs U . V dV Колебания поверхностных атомов в УДЧ происходят с большей амплитудой и меньшей частотой, чем в объеме. Это обусловливает изменение колебательного спектра и увеличение теплоемкости УДЧ по сравнению с массивными образцами. Имеются также отличия в структуре 70 частицы: отсутствие 19 плотной упаковки, изменение расстояния между атомами. По структурным признакам область размеров частиц от 100 до 300 A является переходной. В этой области в металлических частицах возникают два типа упаковки атомов: внутренняя, соответствующая данному типу кристалла, и внешняя – икосаэдрическая критический (икосаэдр размер, – выше двадцатигранник). которого Существует поверхностные структуры На кривой имеется три участка, расположенных в области низких, средних и высоких давлений. При малых p наблюдается линейная зависимость адсорбции от поверхность адсорбента давления свободна, или идет концентрации, активное т. к. заполнение поверхности. В этой области адсорбция прямо пропорциональна давлению в соответствии с законом Генри: k P . Уравнение Генри становятся менее стабильными, чем внутренние, упаковка которых можно получить путем рассмотрения адсорбции из газовой фазы на соответствует структуре данного компактного материала. Переход от основе кинетического подхода. поверхностной структуры к внутренней затруднен кинетически из-за необходимости перестройки окружения большого числа атомов, что делает структуру УДЧ метастабильной. Форма и структура УДЧ неравновесны вещества. и соответствуют Насколько велика энергонасышенному насыщенность следующий пример. При дроблении NaCl молекулярного сравнению взаимодействия с до увеличивается компактными состоянию энергией, говорит 1 109 м энергия 10 7 в материалами. раз по Большая энергонасыщенность приводит к усилению взаимодействия между частицами и к изменению физико-химических и физико-механических свойств вещества. Выделение избыточной энергии приводит к сильному взаимодействию с полимерной матрицей. Для неорганических композитов с УДЧ твердость возрастает в несколько раз, возрастает также ударная вязкость. Неравновесность или метастабильность ультрадисперсного состояния приводит к двум следствиям. Первое следствие состоит в том, что УДЧ взаимодействуют с любыми веществами, в том числе кислородом, водой, азотом, инертными газами по механизму адсорбции и химического взаимодействия. Второе следствие состоит в том, что УДЧ, не имеющие защитного слоя на поверхности, 20 Рассмотрим динамическую картину адсорбционного процесса, поведение молекул в поверхностном слое, т.е. кинетику адсорбции. Кинетические закономерности адсорбции определяют скорость установления равновесия при адсорбции, или сокращенно, скорость адсорбции. При столкновении с поверхностью молекула либо отражается от поверхности под углом, равном углу падения, либо некоторое время остается на поверхности, затем десорбируется. Чем больше времени молекула находится на поверхности, тем длительнее устанавливается равновесие. Иными словами, скорость установления равновесия V увеличивается с уменьшением времени пребывания молекулы на поверхности . Величина пребывания адсорбции молекулы на равна поверхности произведению времени молекул, на число контактирующих с поверхностью в единицу времени. В этом и состоит динамическое уравнение адсорбции, которое записывается следующим образом: n (3.7) Из кинетической теории следует, что n мол Np 2 2MRT см сек 69 (3.8) Энергия притяжения при адсорбции зависит от расстояния в третьей степени вместо шестой, как это имеет место при взаимодействии двух атомов. Такая зависимость указывает на более агрегируют, что хорошо известно из теории устойчивости коллоидных систем. Агрегация коллоидных частиц (УДЧ) характеризуется медленное уменьшение энергии притяжения при адсорбции и на особенностями роста и геометрического строения. Эти частицы дальнодействие адсорбционых сил. Полная потенциальная энергия участвуют взаимодействия при адсорбции выражается уравнением случайного блуждания. Слипание частиц друг с другом (агрегация) B C n r 12 6r 3 наиболее интенсивно протекает на значительном удалении от места U (3.6) в броуновском движении, двигаясь по траектории зарождения коллоидного агрегата, т. е. на его периферии. Поэтому где n - число атомов в единице объема адсорбента. Важными агрегат имеет сильно разветвленную структуру. С увеличением практическим выводом при рассмотрении природы адсорбционных сил размера агрегата ( r ) его плотность ( ) уменьшается, и при r , является вывод о том, что, когда преобладают дисперсионные силы, 0 . Были получены агрегаты оксидных частиц необычайно низкой наблюдается лучшая адсорбция в трещинах и порах, т.к. вблизи адсорбированной молекулы находится большое число атомов твердого тела. Если преобладают электростатические силы, то в трещинах и порах заряды компенсируют друг друга, и наибольший потенциал оказывается на выступах, где и будет преобладать адсорбция, особенно при образовании водородных связей. 3.8. Изотермы адсорбции Вид изотермы адсорбции изображен на рис. 3.10. плотности, когда только 2% объема материала заняты веществом, а 98% приходится на пустоты. Такие материалы называются фрактальным агрегатом или фрактальным кластером. Последний внешне выглядит как неупорядоченная система, но характеризуется внутренним порядком, определяемым фрактальной размерностью df . Фрактальная характеризующая размерность структуру и - это степень дробная открытости величина, коллоидного агрегата. Размерность фрактального кластера, являясь дробной величиной, не совпадает с размерностью пространства, в котором существует кластер (размерность пространства - целая величина). Фрактальную характеристику размерность рыхлости можно агрегата. рассматривать Чем меньше также, фрактальная размерность, тем более рыхлым является фрактальный кластер. Рис. 3.10. Изотерма адсорбции 1 типа. 68 21 как На очень близких расстояниях при перекрывании электронных 1.7. Влияние дисперсности на свойства вещества Основными критериями ультрадисперсного (коллоидного) состояния являются следующие: оболочек атомов, возникает отталкивание, называемое борновским отталкиванием и описываемое эмпирическим соотношением: U от Малая кинетическая подвижность частиц вследствие высокой массы частицы по сравнению с молекулой. Гетерофазность. Адсорбционные явления на поверхности. Стабилизация системы за Высокая чувствительность уравнением Леннард-Джонса U счет к снижения малым добавкам системы характеризуются особыми свойствами. Вследствие малого размера частицы в них не оседают. Рассеяние света такими системами приводит к их мутности. Высокая удельная поверхность таких систем приводит к возрастанию роли поверхностных слоев. По мере дробления в системе происходят качественные изменения. При переходе от грубо дисперсных систем седиментационную к высокодисперсным устойчивость, системы возрастает приобретают прочность и растворимость, растет взрывоопасность. Из-за увеличения кривизны поверхности увеличивается химическая активность. Ультрадисперсные частицы могут на воздухе воспламеняться. С увеличением степени межмолекулярного B C 6 12 , где C - константа r r B притяжения, - константа борновского отталкивания, происходящего при перекрывании электронных орбит, C B 6 - энергия межмолекулярного (дисперсионного) притяжения, r r 12 энергия борновского отталкивания, которое происходит при малых r и электролитов. Высокодисперсные (3.5) Полная энергия межмолекулярного взаимодействия определяется поверхностной энергии третьим компонентом. В r 12 дисперсности изменяются все свойства вещества. С изменением дисперсности изменяются условия протекания многих химических реакций. Так, реакция обжига известняка с повышением дисперсности сдвигается вправо: CaCO3 CaCO CO2 22 обусловлено запретом Паули. Потенциал притяжения всегда отрицателен, а потенциал отталкивания - положителен. Межмолекулярные порядка 10 -9 силы действуют на малых расстояниях м. При адсорбции дисперсионные силы действуют одновременно между молекулами адсорбата и поверхностью, т.е. многими атомами адсорбента. Дисперсионные силы обладают свойством аддитивности, происходит суммирование адсорбционных сил, и суммарный потенциал адсорбции определяется выражением U U i C 1 1 B 12 . 6 r r В результате суммирования парных взаимодействий, т. е. тройного интегрирования по объему адсорбента, степень r уменьшается, и межмолекулярное взаимодействие увеличивается. Поэтому адсорбционные силы значительны, и действуют на больших расстояниях по сравнению с межмолекулярными силами rАД 10 67 7 м. Адсорбент Адсорбат Силы взаимодействия полярный полярный Ориентационные полярный неполярный неполярный полярный неполярный неполярный индукционные дисперсионные Дисперсионные силы проявляются между мгновенными диполями, возникающими при сближении молекул за счет флуктуаций электронной плотности. Резонанс таких флуктуаций приводит к Удаление кристаллизационной воды из грубодисперсного оксида алюминия Al 2 O3 3H 2 O происходит при 473 K , а из коллоидного оксида - на растворяется в соляной кислоте. Ещё одним примером влияния дисперсности на свойства является изменение свойств воды при дроблении. С уменьшением размера капель воды давление пара над каплей увеличивается. При диаметре капель, равном 1 10 выражением: U межмол .взаим . U о р U инд U дисп . ориентационного, индукционного и дисперсионного в общую энергию оказывается, что доля индукционного эффекта составляет не более 5%. Доля ориентационного эффекта зависит от дипольных моментов взаимодействующих молекул. Для таких сильно полярных молекул, как аммиак и вода, ориентационный эффект равен дисперсионному. Следовательно, для неполярных и слабополярных молекул основным типом межмолекулярного взаимодействия является дисперсионное. Различные виды м , отношение давления пара над каплей при pO , p 1,108 . pO Повышенному давлению пара отвечает пониженная температура замерзания капель воды. Это явление имеет большое Если оценить вклад каждого из трех типов взаимодействий притяжения молекул, то 8 данной температуре p к давлению над плоской поверхностью воды уменьшению общей энергии системы, обусловленному притяжением атомов. Потенциал межмолекулярного взаимодействия определяется 100 ниже, т. е. при 373 K . Коллоидное золото межмолекулярного взаимодействия значение в живой природе, обеспечивая жизнеспособность растений при низкой температуре. В ультрадисперсных твердых частицах размером 10 7 м может происходить коренная перестройка расположения атомов. Из-за большой кривизны поверхности возникают значительные внутренние напряжения, что приводит к изменению физических свойств веществ. Так, температура плавления серебра сильно зависит от размера частиц и равна: при размере частиц 5 10 8 м - 973 K , 2 10 8 м - 593 K , тогда как крупные частицы серебра плавятся при 1233 K . характеризуются одним и тем же законом изменения энергии В высокодисперсных системах повышается температура перехода С , где r r6 в сверхпроводящее состояние. Возникает возможность получения притяжения от расстояния между молекулами U пр расстояние между центрами атомов или молекул, C - константа, в которую входят электрические и магнитные характеристики молекул или атомов, соответствующие для каждого эффекта. 66 высокотемпературных сверхпроводников. Явление сверхпроводимости было открыто в 1911 году голландским физиком Камерлинг-Онессом. Он обнаружил, что при температуре, близкой к абсолютному нулю, ртуть почти полностью 23 теряет электрическое сверхпроводящее явления сопротивление, состояние. Для сверхпроводимости, т.е. переходит практического например с в использования целью Циглера-Натта входит титан. Активный центр комплексного катализатора имеет вид: передачи электроэнергии без потерь на большие расстояния, необходимо получать сверхпроводники при более высокой температуре. В 1986-87 годах в Швейцарии, США, Японии, СССР был открыт класс новых керамических материалов, сверхпроводящих при температуре жидкого азота. Эти материалы изготовлены на основе иттрия и являются дисперсными системами. Рис.3.9. В последнее время обнаружены неустойчивые фазы новых керамических материалов, начинающиеся при в 250 K . которых Чтобы наблюдаются сделать их практически доступными, нужно изучить их фазовую структуру и свойства. Уже в настоящее время возможно применение этих материалов в сверхпроводниковой электронике и вычислительной технике. Таким образом, обладает особыми в высокодисперсном свойствами. Это На атоме Ti происходит предварительная координация молекул переходы, состоянии вещество состояние является промежуточным между свободными атомами или молекулами и массивными образцами. мономера. Развитие весь реальный окружающий нас мир состоит из дисперсных систем. Законы коллоидной химии управляют жизнью крошечной клетки Свойства реальных тел и материалов определяются не только их составом, но и коллоидно-химической т.е. фазовой том числе проблем. Так на заводах СК бутадиеновый каучук СКД получается на катализаторах Циглера-Натта. При этом образуется сильно пахнущие, летучие и токсичные олигомеры бутадиена, загрязняющие атмосферу в производственной и жилой зоне. Поэтому на в последние годы осваивается производство каучука на редкоземельном неодимовом атмосферу, не образуются. 3.7. Природа адсорбционных сил значение в природе и технике. Без преувеличения можно сказать, что структурой, в промышленности синтетических каучуков, идет с учетом экологических Дисперсные системы и поверхностные явления имеют громадное организма. промышленности, катализаторе. В этом процессе олигомеры бутадиена, загрязняющие 1.8. Значение коллоидной химии в природе и технике живого химической структурой, 24 размером частиц, их Физическая Ваальсовых адсорбция сил происходит межмолекулярного под действием Ван-дер взаимодействия, которое складывается из ориентационных, индукционных и дисперсионных сил. Ниже показана природа взаимодействия в зависимости от характера адсорбента и адсорбата. Полярным веществом называется вещество, обладающее интенсивным полем межмолекулярных сил. 65 относительным расположением и взаимодействием друг с другом и 3.6. Значение координационных связей при дисперсионной средой. хемосорбции Примерами дисперсных систем в природе являются почва, горные Хемосорбция может быть обусловлена образованием как ковалентных, так и координационных связей. Это показано при изучении адсорбции различных адсорбатов на поверхности металлов. Во всех случаях, независимо от природы адсорбата, наблюдаются определенные закономерности адсорбции. Первая закономерность заключается в том, что интенсивность хемосорбции велика для переходных металлов. Вторая закономерность состоит в том, что, с увеличением атомного номера металла в одной группе интенсивность хемосорбции снижается, т. к. уменьшается возможность образования координационных связей. В качестве примера на рис. 4.8 показано изменение теплоты адсорбции Qa на поверхности металлов первой переходной группы, с увеличением атомного номера металла. породы, облака, дымы, туманы; а в живой природе - биоколлоиды, биомембраны, клетки и ткани, кровь, размер частиц которой 7 10 Такие продукты питания как молоко, мясо, хлеб, а 6 м. также лекарственные вещества тоже являются дисперсными системами. Основу научно-технического прогресса составляют три направления: новые источники энергии, новые материалы и новые информационные системы. Коллоидная химия в настоящее время определяет развитие катализаторы каждого позволяют восстановление воды до предпосылки для водородной энергетики. направления. осуществлять фото- что создает ре- чистой солнеч- водорода, развития Ультрадисперсные экологически Новые химическое композиционные альные но- материалы, называемые нанокомпозитами, включающие металлы, полимеры и керамику, получаются из ультрадисперсных порошков или с использованием ультрадисперсных наполнителей. Компьютеры нового поколения создаются с использованием моно- и мультислоев ПАВ (пленок Ленгмюра-Блоджетт). Высокая прочность всех трех основных классов конструкционных Рис. 3.8. Зависимость теплоты адсорбции Qa на поверхности металлов от атомного номера металла Эти закономерности важны для понимания механизма катализа. Так в состав катализатора стереоспецифической полимеризации материалов (металлических композитов) определяется их керамики фазовой и полимерных структурой, например, соответствующей образованию игольчатых кристаллов одной фазы в матрице другой фазы. Такие игольчатые кристаллы образуются в металлических полимерах. Эти сплавах, цементном кристаллы оказывают камне, кристаллических упрочняющее действие благодаря тому, что микротрещина, зарождающаяся в матрице, при встрече 64 сплавов, с кристаллом прекращает 25 свой рост. Происходит перераспределение напряжения по многим связям, микротрещина одинаковы. совпадают и изотермы адсорбции одного газа на разных разряжается, и для дальнейшей деформации материала требуется адсорбентах. В качестве примера на рис. 3.7 приведена изотерма новое напряжение. Так реализуется общий принцип прочности и адсорбции азота на TiO2 и BaSO4 . усиления материалов - равномерное распределение напряжений по нагруженным связям. Коллоидная химия имеет большое значение в химической технологии. Такие процессы и явления, как дробление, растворение, кристаллизация, флотация, гетерогенный катализ основаны на глубоком изучении поверхностных явлений. В последнее время большое значение в технике и технологии получили мембранные методы разделения сложных смесей: обратный осмос, ультрафильтрация, Движущими силами, испарение вызывающими через мембрану, перенос вещества в этих процессах, являются разность концентраций, давлений, химических или электрических потенциалов. Этими методами разделению подвергаются как газовые, так и жидкие смеси. В химической и нефтехимической промышленности мембранные методы используются для разделения смесей высоко- и низкомолекулярных соединений, эмульсий, выделения гелия и водорода из природных газов, кислорода из воздуха. В электронной промышленности, потребляющей большоеколичество ультрачистой воды, мембранным методом получают воду, по чистоте превосходящую бидистиллат. В пищевой промышленности мембранные методы применяются для получения высококачественного сахара, стабилизации пива и виноградных вин, очистки воды методом обратного осмоса для приготовления высококачественной водки, Рис. 3.7. Изотерма адсорбции диализ. концентрирования N2 на TiO2 (0) и BaSO4 (x). Адсорбция зависит от величины поверхности адсорбента и от энергии взаимодействия между поверхностью и газом. Энергия взаимодействия характеризуется теплотой физической адсорбции, которая примерно равна теплоте конденсации газа и не зависит от адсорбента. Решающим фактором в физической адсорбции является не природа адсорбента, а величина его поверхности. В отличие от физической адсорбции хемосорбция специфична, т.е. данное вещество хемосорбируется только на определенных адсорбентах. В хемосорбции более важен энергетический фактор, а не величина поверхности. При хемосорбции адсорбция возможна самопроизвольного уменьшения энергии Гиббса всей системы, что может привести даже к увеличению поверхностной энергии. Это возможно в том случае, если G хим G . S фруктовых и овощных соков. 26 вследствие 63 В микробиологической и медицинской промышленности эти методы применяются для очистки и выделения биологически активных веществ, лекарственных веществ, для очистки крови. Мембранные методы имеют большое значение для охраны окружающей среды. производства путем Они позволяют организации создавать замкнутого безотходные водооборота и утилизации ценных вредных веществ. Из сточных вод сыроваренных заводов извлекаются белок, лактоза и витамины. Мембранные методы широко применяются для опреснения соленой воды. В 1970 году Рис. 3.6. Изобары физической адсорбции ( a ) и хемосорбции ( в ) этими методами получали всего 1% пресной воды, в 1980 году – При низкой температуре протекает только физическая адсорбция, а хемосорбция не протекает. При высокой температуре протекает хемосорбция, а физическая адсорбция пренебрежимо мала. 50% , а в настоящее время почти вся опресненная вода получается мембранными методами. Особое значение коллоидно-химические явления имеют в Кривая (a) соответствует равновесной физической адсорбции, (b) переработке полимеров. Примерами типично коллоидных полимерных - хемосорбции. На обоих этих участках адсорбция обратима и систем являются кристаллические полимеры, дисперсии, латексы, равновесна. На участке (c) протекают оба процесса: физическая наполненные адсорбция и хемосорбция. Для хемосорбции на этом участке значения пластизоли, нетканые материалы и другие. равновесной адсорбции велики, но скорость установления равновесия мала. смеси полимеров, блок-сополимеры, Кристаллические полимеры имеют ряд существенных отличий по сравнению Степень равновесной адсорбции при температуре, при которой полимеры, с проявляются низкомолекулярными уже на стадии кристаллами. образования Эти отличия кристаллов. Если скорость хемосорбции низка, но не пренебрежимо мала, представлена низкомолекулярные жидкости кристаллизуются только при охлаждении неравновесной кривой (с), расположение которой зависит от времени, ниже температуры кристаллизации, то полимеры кристаллизуются необходимого для достижения равновесия. также при растяжении. Кристаллизация полимеров при растяжении - Четвертое состоит в отличие том, что физической адсорбции от физическая адсорбция хемосорбции неспецифична, а причина высокой прочности резин из натурального, синтетического кристаллизующихся каучуков: полиизопренового, цис- хемосорбция специфична. Неспецифичность физической адсорбции полибутадиенового, означает, что данное вещество примерно одинаково адсорбируется 150 160 кг см . Каучуки, не способные кристаллизоваться, например на разных адсорбентах. Это проявляется в том, что теплоты физической адсорбции данного газа на различных адсорбентах 62 полихлоропренового, которая достигает бутадиен-стирольный, позволяют получать резины с прочностью всего 27 23 30 кг см . Гигантские молекулы полимеров состоят Эти из кинетических единиц, называемых сегментами. Кристаллические полимеры однофазны по отношению к макромолекуле. В то же время кривые объясняют наблюдающуюся обычно быструю сорбцию в начале процесса и медленную в дальнейшей стадии. Кривая (2) отвечает хемосорбции, идущей для первых порций ( 0) кристаллические полимеры по отношению к сегменту представляют адсорбата собой уменьшающейся по мере заполнения поверхностного слоя (кривая (3) двухфазную систему, в которой нельзя отделить с выделением значительной энергии, 0,8 ). При приближении молекулы к поверхности в области кристаллическую фазу от аморфной, в отличие от низкомолекулярных для систем. Это является следствием того, что отдельные полимерные больших расстояний процесс идет по кривой (1) (скорость велика, молекулы EQ 0 ), и переход на кривую (2) происходит без барьера. В большого размера находятся одновременно в кристаллической и аморфной фазе. Таким образом, можно говорить о том, что в полимерах молекулы больше, чем кристалл, по своему размеру. Кристаллическая фаза переходит в аморфную непрерывно, в кристаллическом полимере отсутствуют четкие границы раздела между фазами. Кристаллизация в полимере протекает во времени. Вначале кристаллизуются наиболее подвижные участки макромолекул, затем менее подвижные. Это приводит к двум важным следствиям. Вопервых, полимерные кристаллы плавятся не при одной температуре, как низкомолекулярные, а в интервале температур. Вспомним, что в органической химии четкая температура плавления является критерием чистоты вещества. Во-вторых, интервал плавления зависит от возраста кристалла. Чем дольше хранился кристалл, чет выше его интервал плавления. Так, натуральный каучук, пролежавший в течение 30 лет на дне Атлантического океана, имел температуру плавления 60 С по сравнению с 10 С для кристаллов каучука, хранившегося дальнейшем, при значительной степени заполнения поверхности, для перехода от кривой (1) к кривой интерес с коллоидно-химической точки хемосорбция называется активированной. равномерно 28 распределяются в Величина энергии хемосорбции и сильно отличается для разных систем. Она является очень низкой для хемосорбции водорода на металлических поверхностях. Энергия активации входит в выражение для скорости хемосорбции типа уравнения Аррениуса: V V0 e E q RT . Если энергия активации хемосорбции велика, то скорость хемосорбции при низкой температуре настолько мала, что протекает только физическая адсорбция. На рис. 3.6 показано изменение степени адсорбции газа на твердой поверхности в зависимости от изменения температуры при постоянном давлении (изобара адсорбции). зрения полимера с твердыми, жидкими и газообразными веществами, относительно преодолеть активации зависит от формы кривых физической адсорбции и представляют наполненные полимеры. Наполнение - это сочетание которые требуется активационный барьер, равный энергии активации хемосорбции. Такая в течение одного года. Большой (3) объеме 61 физической адсорбции, а теплота хемосорбции значительно превышает теплоту физической адсорбции. непрерывной Пересечение кривой 1 с 2 и 3 отражает переход от физической адсорбции к химической. Правый и левый верхние участки кривых 2 и кривая хемосорбции полимерной фазой (матрицей). Газонаполненные полимеры представляют собой пенорезины или пенопласты. Твердые наполнители бывают зернистые, такие как технический углерод (сажа), диоксид кремния, мел; пластинчатые - тальк, слюда, 3 и левый верхний участок кривой 1 не реализуются. Результирующая образующейся композиции и имеют четкую границу раздела с имеет максимум, графит; волокнистые. На границе раздела фаз в наполненных образующийся при пересечении кривых 1 и 3 и соответствующий полимерах энергии активации адсорбции. При пересечении кривых 1 и 2 смачивание, адгезия, адсорбция, полимеризация на поверхности максимум отсутствует, что соответствует протеканию процесса без наполнителя. При этом адсорбируется несколько молекул полимера и энергии активации. образуется Таким образом кривая (1) описывает в себя Вандер-Ваальсовы энергии M и газом X 2 . Она физического взаимодействия между металлом включает изменение (диполь-дипольные и лондоновские) силы притяжения и борновские силы отталкивания. большое значение поверхностный имеют слой поверхностные значительной явления: толщины. Если толщина поверхностного слоя на границе раствора соли с воздухом равна 5 10 10 м , кварца с полисилоксаном - 10 8 м , то межфазные слои в полимерах имеют толщину свыше 10 7 м . В полимерах проявляется подвижность макромолекул в целом и ее отдельных Кривые (2) и (3) описывают хемосорбцию, в которой молекула участков - сегментов, т. е. полимеры имеют двойственную природу. адсорбата вначале диссоциирует на 2 атома X . Поэтому для Вследствие этого в межфазных слоях на поверхности наполнителя протекания хемосорбции необходимо затратить энергию, равную следует различать сегментальный слой небольшой толщины и энергии диссоциации. Величина этой энергии показана на больших значительный по размерам граничный слой (рис. 1.6). расстояниях от поверхности. Кривые (2) и (3) характеризуются относительно глубоким минимумом, соответствующим теплоте хемосорбции и находящемся на более близком расстоянии от твердой поверхности, чем относительно мелкий минимум на кривой физической адсорбции. Как правило, начальной стадией хемосорбции является физическая адсорбция. При отсутствии физической адсорбции энергия активации равна адсорбируемого газа. высокой Если энергии молекула диссоциации газа вначале молекул физически адсорбируется, то она приближается к поверхности по пути с низкой Рис. 1.6. Межфазный и переходный слой в полимерах. !-Наполнитель, 2-сегментальный слой, 3-переходный слой, затратой энергии. 60 29 4-полимер. На поверхности частицы наполнителя вследствие ограничения подвижности макромолекул изменяется их конформация. Это в свою очередь влияет на близлежащие макромолекулы, расположенные в объеме матрицы. В случае кристаллического полимера небольшое количество твердых частиц (доли % по объему) изменяет кристаллическую структуру всего полимера, что указывает на сильное дальнодействие поверхности. Наполнители, усиливающими. сильно повышающие Наибольшее значение прочность, имеет называются усиление каучука техническим углеродом (сажей). Сажа образует в матрице каучука цепочечные и фрактальные структуры, которые причиной повышения прочности является притупление вершины разрастания трещины, повышение энергии, рассеиваемой в объеме, по линии разрыва. Поэтому происходит выравнивание Особый класс коллоидных систем типа полимер в полимере образуют смеси полимеров. Они имеют двухфазную структуру, высокую устойчивость вследствие огромной вязкости и малого межфазного натяжения, развитый межфазный слой. Свойства смесей от следующих коллоидно-химических параметров: соотношения объемов дисперсной фазы и дисперсионной среды, природы дисперсной фазы и матрицы, размера и формы частиц дисперсной фазы, интенсивности взаимодействия полимеров на границе раздела фаз. Для двухфазных 0 (2), 0,8 (3) Рассмотрим в качестве примера изменение потенциальной энергии молекулы газа X 2 с изменением расстояния от поверхности металла, на которой она адсорбируется физически (кривая 1) и химически (кривые 2 и 3) при разной степени заполнения поверхности напряжения при деформации. зависят хемосорбции при способствуют ориентации молекул каучука, вследствие чего повышается прочность. Другой Рис. 3.5. Кривые потенциальной энергии для физической адсорбции (1) и смесей каучуков характерен эффект взаимоусиления, заключающийся в увеличении динамической выносливости (N-число циклов до разрыва) (рис. 1.7). 30 адсорбента . При сближении молекулы с поверхностью, потенциальная энергия уменьшается вследствие действия Ван-дер-Ваальсовых сил притяжения. По положению минимума на кривой можно определить минимальное расстояние от поверхности, а по величине этого минимума – теплоту физической адсорбции. При дальнейшем уменьшении расстояния потенциальная энергия увеличивается вследствие проявления сил отталкивания (борновских сил). При хемосорбции молекула предварительно диссоциирует на атомы Положение минимумов на кривых 2 и 3 X. соответствует оптимальному расстоянию адсорбированных атомов от поверхности, а величины этих минимумов – теплоте хемосорбции. Как видно, при хемосорбции молекула ближе подходит к поверхности, чем при 59 при хемосорбции образуются мономолекулярные слои. При этом следует иметь в виду, что в отличие обычной химической реакции, протекающей на поверхности, когда возможны диффузия реагента вглубь объемной образования фазы, двумерного хемосорбция является процессом химического соединения, т. к. хемосорбционный слой препятствует диффузии реагента. В качестве примера рассмотрим хемосорбцию кислорода на угле. Окисление поверхностных атомов углерода приводит к образованию различных поверхностных оксидов: Рис. 1.7. Зависимость динамической выносливости резины при определенном составе смеси. Рис. 3.4. Схема хемосорбции на угле. Прочная пленка оксида препятствует дальнейшему проникновению кислорода вглубь твердой фазы. Третье различие между физической адсорбцией и хемосорбцией состоит в различии кривых потенциальной энергии, вытекающем из разной природы связей, образующихся между адсорбентом и адсорбатом. Кривые потенциальной энергии при адсорбции двухатомного газа X 2 на металле M показаны на рис. 3.5. 58 31 Вследствие высокого значения теплоты хемосорбции процесс 2. Поверхностные явления и адсорбция хемосорбции трудно обратим. Физическая же адсорбция легко 2.1. Классификация поверхностных явлений обратима, процесс идет без энергии активации и равновесие Поверхностные явления следует рассматривать, как центральную часть курса коллоидной химии. Как уже указывалось выше, в поверхностном слое поверхностная энергия поверхностного слоя. приповерхностных связей атомов адсорбента, вследствие чего при F S . Это приводит к повышенной активности десорбции выделяется не адсорбат, а другое соединение. Так, при избыток Поверхностные свободной явления энергии определяются происходить при совместном действии молекулярных и внешних сил (сил тяжести). Это наблюдается на границах раздела твердой и жидкой фаз и сопровождается искривлением жидких поверхностей раздела. Такие поверхностные явления называются капиллярными (см. с.10). Поверхностные явления в твердых телах происходят прежде всего внешней поверхности тела. К таким явлениям относятся смачивание, адгезия (прилипание), трение, коррозия. Наряду с этим, поверхностные явления происходят и на внутренних поверхностях, образующихся Необратимость хемосорбции связана также с ослаблением - появляется действием химических или межмолекулярных сил. Они могут также на устанавливается быстро. вследствие дефектов кристаллической решетки, зернистой структуры вещества. Форма реализации поверхностных явлений не зависит от размера поверхности. Рассмотрим закономерности поверхностных явлений, которые являются общими для микро- и макроповерхностей. Объединенное уравнение 1-го и 2-го начал термодинамики позволяет классифицировать поверхностные явления. Запишем это уравнение в форме: десорбции кислорода, хемосорбированного на угле, десорбируется не кислород, а оксиды углерода. Вследствие взаимодействия поверхностных атомов углерода с кислородом резко уменьшается прочность их связи с другими атомами углерода. Поэтому при десорбции отрывается оксид углерода, а не кислород. Вещества, адсорбированные на ткани за счет физической адсорбции, могут быть легко удалены путем проветривания (нафталин, бензин и др.). Если же вещества адсорбировались за счет хемосорбции, то удалить их чрезвычайно трудно или просто невозможно. Так, анализ волос Ньютона, проведенный в 1979 году, показал повышенное содержание ртути в них. Действительно, Ньютон в течение 18 лет работал со ртутью, и это, возможно, послужило причиной его тяжелого заболевания за 33 года до смерти. Волосы Наполеона содержали повышенное количество мышьяка, источником которого, как считают историки, послужили обои его спальни. Очевидно, мышьяк и ртуть связаны с кератином, из которого состоят волосы, химическими связями, т.е. хемосорбционно. Второе различие между физической адсорбцией и хемосорбцией состоит в том, что физическая адсорбция может быть как монослойной, так и многослойной. Многослойная физическая адсорбция протекает при давлении насыщенного пара и переходит в конденсацию. В отличие от этого, хемосорбция всегда монослойна, 32 57 Так как адсорбция обратима, то она подчиняется правилу Ле (2.1) Шателье. При повышении температуры процесс сдвигается в сторону десорбции, идущей уменьшается. с поглощением Адсорбция имеет тепла, т. е. отрицательный адсорбция температурный где G - энергия Гиббса, S - энтропия, коэффициент. С повышением температуры равновесные значения адсорбции уменьшаются. Изотермы адсорбции при высокой температуре расположены ниже изотермы, соответствующей более низкой температуре (рис. 3.3). соответствии с уравнением: K P ge где RT взаимодействия. Хемосорбция обусловлена образованием химических связей между адсорбентом и адсорбатом. Между физической адсорбцией и хемосорбцией имеется ряд существенных различий. Первое различие состоит в том, что адсорбции и хемосорбции сильно от- личаются. Теплота физической адсорбции газов обычно равна теплоте их конденсации, а теплота хемосорбции много больше. Так, при адсорбции азота Уравнение (2.1) выражает приращение энергии Гиббса через на железе H физ 10 кДж / моль , H хим 150 кДж / моль , H конд 5,7 кДж / моль . 56 сумму приращений других видов энергий. Гиббса. Такой переход имеет место при адсорбции, а также лежит в Физическая адсорбция обусловлена действием физических, т. е. физической q - заряд. Стрелкой 1 указан переход поверхностной энергии в энергию физическую адсорбцию и химическую адсорбцию, или хемосорбцию. теплоты ni - число молей, - электрический определенным поверхностным явлениям. В зависимости от природы адсорбционных сил различают межмолекулярного - поверхностное натяжение, s - поверхность, Превращение поверхностной энергии в другой вид энергии отвечает (3.4) 3.5. Физическая адсорбция и хемосорбция сил химический потенциал, алгебраическую K р - константа равновесия адсорбции, q - теплота адсорбции. вандерваальсовых i - потенциал, Адсорбция возрастает с увеличением теплоты адсорбции в q объем, p - давление, T - температура, V - основе изменения реакционной способности с изменением дисперсности. Стрелка 2 обозначает переход поверхностной энергии в теплоту, который происходит при изотермической перегонке, адсорбции и смачивании и выражается теплотой конденсации, смачивания или адсорбции. Переход поверхностной энергии в механическую указан стрелкой 3. Такой переход наблюдается при адгезии, капиллярности, адсорбции. Стрелка 4 указывает на переход поверхностной энергии в химическую, что соответствует таким поверхностным явлениям, как адсорбция, коррозия. Наконец, переход поверхностной энергии в электрическую указан стрелкой 5. Такой переход приводит к образованию электрического заряда поверхности и двойного электрического слоя и соответствует группе электрокинетических явлений: электрофорезу, электросмосу, потенциалам течения и оседания. 33 уменьшается (рис. 3.2). В первую очередь газ адсорбируется наиболее 2.2. Основы термодинамики поверхностного слоя Во введении отмечалось, что коллоидные системы обладают сильно развитой поверхностью раздела между фазами. В поверхностном или межфазном слое молекулы принадлежат обеим активными участками поверхности, и при этом выделяется наибольшее количество тепла. По мере насыщения активных центров адсорбция происходит на менее активных участках поверхности. фазам, они контактируют не только с себе подобными, но и с молекулами другой фазы. Поэтому вещество в поверхностном слое находится в особом состоянии, и необходимо определить вклад поверхностного слоя в термодинамические свойства всей системы. Для этого необходимо рассмотреть свойства и состав поверхностных слоев, поверхностную энергию, и другие термодинамические функции. При таком положения рассмотрении будем иметь в виду, что основные термодинамики объемных фаз применимы и Рис.3.2. Зависимость дифференциальной теплоты адсорбции от величины к адсорбции. термодинамике поверхностного слоя. При физической адсорбции значения теплоты адсорбции невелики. Так, значения дифференциальной теплоты адсорбции не превышает 10 ккал/моль. Поэтому физическая адсорбция является обратимым процессом, находящимся в равновесии с обратным процессом десорбции. Рис. 2.1. Простейшая гетерогенная система. Рассмотрим гетерогенную систему, состоящую из трех частей: фазы , фазы объемными фазами и поверхностного слоя и Причиной адсорбции являются межмолекулярные силы, причиной десорбции - тепловое движение молекул. s мол . Между двумя образуется поверхностный или граничный межфазный слой. Толщина этого слоя равна . Поверхностный слой является переходной областью от одной фазы к другой: он имеет одну часть в первой фазе, в другую - во второй. Отметим, что фазы как межфазный слой и однородны на всем протяжении, тогда неоднороден. 34 Рис. 3.3. Влияние температуры на изотерму адсорбции. 55 Рассмотрим основные отличия свойств поверхностного слоя от свойств объемных фаз и причины этих отличий. 1. Первое отличие межфазного слоя от объемных фаз состоит в том, что удельная внутренняя энергия слоя отличается от внутренней энергии объемных фаз, т. к. в каждой фазе взаимодействуют молекулы одного сорта, а в поверхностном слое взаимодействуют разные молекулы. dU dU dU dV s dV dV Рис. 3.1. Зависимость теплоты адсорбции от величины адсорбции. 2. Взаимодействие молекул в поверхностном слое происходит в Различают адсорбции. количество количества Qинт дифференциальную Интегральная тепла, и теплота адсорбции выделившееся адсорбата на интегральную 1 - теплоту это при адсорбции кг адсорбента несимметричном силовом общее межмолекулярных сил, действующая на молекулу, находящуюся в данного поверхностном слое, не равна нулю. Поэтому молекулы стремятся qинт ; уйти с поверхности в объем, и наоборот, при увеличении Зависимость интегральной теплоты при этом затрачивается работа против межмолекулярных сил адсорбции от величины адсорбции не линейна (рис. 3.1), т. к. dA ds мол . поверхность поверхностной энергии энергетически неоднородна. Вначале адсорбция идет на более активных центрах, и выделяется больше происходит тепла, затем количество выделяющегося тепла снижается. энергии Дифференциальная теплота адсорбции - это тепло, выделившееся при дополнительной адсорбции малого количества адсорбата в расчете на моль адсорбата Дифференциальная теплота адсорбции q диф dQ Дж . da кг адсорбата характеризует не весь адсорбционный процесс, а некоторую его стадию, для которой адсорбция достигла Равнодействующая поверхности происходит вывод молекул из объема на поверхность, Q Дж . m кг адсорбента адсорбента поле. величины Эта сгущение, работа увеличению свободной F S . Таким образом, в поверхностном слое увеличение свободной поверхностной dF S 0 , F S T ,Ui ,V S . Следовательно, плотность свободной энергии в объемных фазах и поверхностном слое различна. F F F V s V V a . Дифференциальная теплота адсорбции с увеличением количества адсорбированного вещества 54 равна 35 Адсорбция существуют уменьшает на небаланс поверхности и, сил притяжения, следовательно, которые свободную поверхностную энергию гетерогенной системы. Основное различие между твердыми и жидкими поверхностями заключается в том, что твердая поверхность неоднородна по активности и свойства ее в некоторой степени зависят от предыстории поверхности. 3.4. Адсорбция как обратимый экзотермический процесс Рис.2.2. Межмолекулярные взаимодействия в объеме и на поверхности. энергии В адсорбционном слое молекулы газа способны к перемещению происходит изменение концентрации компонентов в поверхностном лишь в двух измерениях, поэтому адсорбция газа сопровождается слое. Это изменение может быть как положительным, так и уменьшением энтропии, т. е. S 0 . Условием протекания адсорбции отрицательным. Состав поверхностного слоя отличается от как самопроизвольного процесса является уменьшение энергии 3. Вследствие избытка свободной поверхностной n ni ni i . В поверхностном V s V V состава объемных фаз Гиббса, т. е. G 0 . Из термодинамической зависимости G H T S следует, что теплота адсорбции должна быть слое концентрируется компонент, уменьшающий избыток свободной отрицательной, т. е. адсорбция газов или паров на твердом теле поверхностной энергии. всегда является экзотермическим процессом. Поэтому степень 4. Значения удельной энтропии поверхностного слоя и объемных адсорбции газа в равновесных условиях увеличивается с понижением S S S . При контакте газа с V s V V температуры. Теплота адсорбции может быть определена прямым фаз различны т.е жидкостью или твердым телом поверхностный слой разрыхлен. На поверхности жидкости постоянно протекают процессы испарения и конденсации. Так, например, среднее время жизни молекулы воды на поверхности составляет 10 7 сек. Из-за возможности выхода молекул в менее плотную фазу их число степеней свободы увеличено, поэтому s . S уд S уд 36 калориметрическим методом и рассчитана из обратимой изотермы адсорбции по уравнению Вант-Гоффа H адс д ln P RT 2 дT V (3.3) Причиной выделения тепла при адсорбции является уменьшение энергии поверхности адсорбента. 53 Основным законом, определяющим поведение компонентов при адсорбции, является закон распределения Нернста-Шилова . Величина адсорбции компонентов зависит от температуры и концентрации или давления. При контакте жидкости с твердым телом происходит ориентация молекул жидкости, энтропия уменьшается т.е. образом, поверхностный термодинамических A f [T , C (или p)] (3.2) слой свойств, s S уд S уд . Таким характеризуется который может избытком быть как положительным, так и отрицательным. Поэтому различают следующие виды адсорбционных зависимостей: A f (C ) или адсорбции; A f ( p) при T const - изотерма A (T ) при p const - изобара адсобции и P (T ) или C (T ) - изостера адсорбции При рассмотрении адсорбции на различных поверхностях раздела: газа с твердым телом, раствора с твердым телом и раствора с газом следует отметить, что адсорбция газа на твердой поверхности является простейшим случаем, удобным для теоретического Рис. 2.3. Изменение энтропии в поверхностном слое. рассмотрения, т.к. в адсорбционном процессе участвуют только два компонента. Когда газ или пар приводятся в контакт с чистой твердой поверхностью, некоторое количество их связывается с поверхностью в 2.3. Интенсивные свойства гетерогенных систем форме адсорбционного слоя. Твердое тело является адсорбентом, а Рассмотрим термодинамические свойства гетерогенной системы, газ или пар - адсорбатом. Одновременно может наблюдаться состоящей из трех частей: фаз , и поверхностного слоя S. Эти поглощение газа объемом твердого тела, т.е. абсорбция. свойства делятся на интенсивные и экстенсивные. Интенсивными от свойствами называются такие свойства, которые выравниваются температуры, давления газа и эффективной поверхности адсорбента. при составлении сложной системы из более простых систем. Поэтому лучшими адсорбентами являются высокопористые вещества, Интенсивные свойства - это такие физические характеристики, такие численные значения которых не зависят от количества вещества. К Степень как адсорбции в активированный состоянии уголь и равновесия силикагель. зависит Их удельная 2 поверхность достигает 1000 м /г. Зависимость между равновесным интенсивным свойствам относится давление количеством адсорбированного газа при данной температуре и химический потенциал давлением газа называется изотермой адсорбции. G F , V V 52 , P , температура T , удельная энергия или плотность энергии, . 37 Условия равновесия гетерогенной системы с поверхностным слоем таковы же, что и системы, состоящей из объемных фаз. Эти условия выражаются уравнениями: T S T T , S i i i , p s p p . Происходит выравнивание интенсивных величин - адсорбатом или адсорбтивом. Если адсорбент находится в виде фазы, то адсорбат находится в молекулярно-дисперсном состоянии. 3.2 Количественные характеристики адсорбции Избыточная i -го компонента расчитаная на концентрация температуры, химического потенциала и давления. Выравнивание единицу площади разделяющей поверхности называется гиббсовой этих величин буквально означает их равенство во всех частях адсорбцией: системы. Выравнивание остальных интенсивных термодинамических i свойств приводит к появлению избытка свойств в поверхностном слое. Этот избыток может быть как положительным, так и отрицательным. Гиббсова, или ni S моль м2 (3.1) абсолютная адсорбция, является удельной величиной, применяемой для описания состава поверхностного слоя независимо от его площади. Другой характеристикой адсорбции является поверхностная концентрация адсорбата , равная общей концентрации вещества в поверхностном слое рассчитанной на единицу площади поверхности и выражаемая в моль . При малых концентрациях адсорбата Г i и м2 совпадают, при больших - различаются. Рис. 2.4. Изменение плотности свободной энергии на межфазной границе Когда поверхность адсорбента неизвестна, величину адсорбции лиофобной системы. измеряют емкостью поверхностного слоя a и выражают в z - расстояние от границы раздела фаз; Это также общее количество вещества в поверхностном слое, - толщина межфазного слоя. В качестве примера изменения интенсивных свойств рассмотрим изменение плотности свободной поверхностной энергии f лиофобных и лиофильных систем перпендикулярно границе раздела фаз и (рис 2.4, 2.5). элемента рассчитанное на единицу массы. 3.3. Типы адсорбционных зависимостей С термодинамической точки зрения процессы адсорбции на различных границах раздела фаз не отличаются друг от друга. В объеме каждой фазы значение расположения моль . кг объема, 38 f постоянно и не зависит от т. к. фаза характеризуется Наблюдаемые различия относятся к структуре адсорбционного слоя и механизму процесса адсорбции. 51 определенными и постоянными по объему физико-химическими 3. Общие закономерности адсорбции f свойствами. 3.1. Понятие об адсорбции Для рассмотрения причин адсорбции важна зависимость состава слоя (произведения поверхностном слое dF S от dn ), изменение которого может фундаментального уравнения Гиббса для плоского поверхностного слоя следует, что межфазный слой обогащается тем компонентом, который характеризуется меньшей работой извлечения из объема и снижает поверхностное натяжение. Это приводит к убыли свободной поверхностной энергии компонента на поверхности f растет вследствие несимметричного силового энергетического уровня одной фазы привести к изменению других характеристик поверхностного слоя. Из В поля и сгущения свободной поверхностной энергии. Переход от S i i F f f f const , 0; 0; 0 . V x y z другой f фазы происходит f к энергетическому уровню через энергетический барьер, отвечающий избытку (сгущению) свободной энергии в поверхностном слое. Величина избытка свободной энергии равна площади заштрихованного «языка». dF S 0 . Изменение концентрации раздела фаз по сравнению с концентрацией в объеме называется адсорбцией. Адсорбцию можно определить как процесс выравнивания химических потенциалов компонентов между поверхностью и объемом, приводящий к изменению концентрации на поверхности. При установлении адсорбционного равновесия давление, температура и химические потенциалы компонентов в поверхностном слое и в объемных фазах p p p s , выравниваются T T T ; . В отличие от других процессов S S (диффузия, осмос) адсорбция идет не в сторону выравнивания концентраций, а в сторону их расхождения. Происходит накачка поверхностного слоя компонентом, снижающим поверхностное натяжение. Фаза, на адсорбентом. которой Вещество, происходит которое 50 адсорбция, называется адсорбируется, называется Рис. 2.5. Изменение плотности свободной энергии на межфазной границе лиофильной системы. Когда f f 0 , т.е. для лиофобных систем (рис 2.4), для разнородных фаз при слабом их взаимодействии, избыток свободной энергии велик, межфазного заштрихованная слоя мала, т.к. площадь велика, молекулярные силы но толщина убывают с расстоянием, взаимодействие между фазами отсутствует или оно мало. Для лиофобных систем толщина межфазного слоя составляет 39 всего (1÷10)10-10 м. В лиофильных системах (рис 2.5) фазы являются родственными, они сильно f взаимодействуют, f 0. Значение межфазного поверхностного натяжения в лиофильных m 0,1 эрг / см системах мало и составляет величину 2 . взаимодействия фаз, поверхностный слой. Химический потенциал характеризует скорость, с которой меняется свободная энергия при изменении концентрации меньше, заштрихованная площадь меньше (рис 2.5). сильного Химический потенциал - это мольное приращение свободной энергии при постоянном объеме при переходе i-го компонента в Избыток свободной поверхностной энергии в таких системах Вследствие F s 3. j. N i S ,T , N j Ni проникновения данного вещества. Химический потенциал является движущей силой молекулярного взаимодействия глубоко в объем каждой фазы, химических реакций. Аналогично толщина поверхностного слоя в лиофильных системах велика. химический потенциал можно выразить как частную производную Поверхностный слой более размыт, имеет большую протяженность. любой характеристической функции по концентрации. По энергетическим параметрам он приближается к фазам. 2.4. Экстенсивные свойства гетерогенных систем Экстенсивными называются такие свойства, которые при составлении суммируются. сложной системы Экстенсивные из более свойства - простых это систем аддитивные характеристики, их численные значения зависят от количества вещества. К экстенсивным свойствам относятся масса m , объем V , поверхность s , количество любого компонента ni , внутренняя энергия U , свободная энергия F , энтропия S . Для гетерогенной системы с поверхностным слоем каждое экстенсивное свойство является суммой трех величин, характеризующих фазы и поверхностный слой. U U U U S F F F F S S S S S S ni ni ni ni 40 S 49 поверхностному натяжению U H F G s S ,V ,ni s S ,P ,ni s T ,V ,ni s T ,P ,ni V V V V S Для рассмотрения термодинамики поверхностного слоя и вклада частная поверхностного слоя в термодинамические свойства всей системы производная от любой характеристической функции по площади применяются два метода: метод избыточных величин и метод слоя межфазной конечной толщины. Таким образом, поверхностное поверхности при натяжение постоянных есть соответствующих параметрах. Наиболее 2.5. Метод избыточных величин Гиббса часто поверхностное натяжение производную от энергии Гиббса, ибо условия осуществимы экспериментально. Для выражают через p и T const легко конденсированных систем можно пользоваться и производной от энергии Гельмгольца, т.к. изменение объема от давления в конденсированных системах мало. Единицы измерения поверхностного натяжения: Для определения характера изменения термодинамических свойств в поверхностном слое необходимо знать его протяженность, т.е. объем или толщину. Свойства поверхностного слоя идентичны свойствам фазы на бесконечно большом расстоянии от поверхности раздела. Толщина поверхностного слоя неизвестна, неопределенна, т. к. поверхностный слой переходит в объемную фазу Дж Н м Н в Си м м2 м2 непрерывно. Значение трудно определить экcпериментально вследствие малой величины и большой погрешности определений или эрг дин см дин в СГС см см 2 см 2 рассчитать теоретически. У. Гиббс в 1876 г. предложил метод описания термодинамики F S S . Экспериментально доказано, что на границе T S , N S 2. i поверхностного слоя, основанный на исключении неопределенности значения . Гиббс от системы поверхностное поверхностью, которая проводится внутри поверхностного слоя. Фазы т. к. увеличивается расстояние между молекулами и уменьшается межмолекулярное взаимодействие. F S 0 . Следовательно, 0и S S 0 . T T Поверхностный слой на границе жидкости или твердого тела с и включают часть поверхностного слой к идеализированной, уменьшается, поверхностный перешел жидкости или твердого тела с газом с повышением температуры натяжение заменив реальной слоя разделяющей и считаются однородными вплоть до разделяющей поверхности. Гиббс предложил относить все изменения термодинамических параметров в слое по сравнению с объемными фазами к разделяющей поверхности, не газом обладает избыточной энтропией, которая всегда имеющей объема, или толщины. Гиббс ввел два понятия: поверхность положительна. Причиной этого является переход молекул в менее разрыва и разделяющую поверхность. плотную фазу, молекулы имеют больше степеней свободы. 48 41 В этих выражениях у i нет индекса, т.к. при равновесии значения химического потенциала в обеих фазах выравниваются. Вычитая из выражения (2.4) выражения (2.5) и (2.6) и учитывая, что экстенсивные свойства (V , S , ni , F ) суммируются и что при достижении равновесия i i i S i , получим dF S ds S S dT i dni Рис. 2.6. Метод избыточных величин Гиббса членов: работы увеличения поверхности раздела фаз, энтропийного Поверхностный слой Гиббс называет поверхностью разрыва, под этим неоднородный тонкий слой, разделяющий объемные фазы и обладающий конечной толщиной и объемом. Разделяющая поверхность – математическая поверхность, члена, учитывающего изменение связанной энергии системы и члена, учитывающего вещественный обмен между фазами и поверхностным слоем, т.е. состав поверхностного слоя. Проанализируем это уравнение: воспроизводящая форму поверхности разрыва и располагающаяся параллельно ей. воображаемая Разделяющая поверхность, непрерывности в плоскостях на поверхность которой - фиктивная, происходит разрыв m, F , S , состава. Каждая точка вещества на поверхности находится в одинаковых условиях. Положение поверхности фиксируют, выбирая определенную величину адсорбции на поверхности. Разность между соответствующими экстенсивными величинами в реальной и идеализированной системе представляет собой избыточную величину, которую относят к разделяющей поверхности. Посредством этих избытков выражаются все экстенсивные параметры в методе Гиббса, поэтому этот метод называется методом избыточных величин. Фактически величины экстенсивных параметров для всей системы в целом несколько отличаются от их суммы для двух объемных фаз. 42 (2.7) Свободная энергия поверхностного слоя складывается из трех a-реальная поверхность, b-идеальная поверхность понимая S 1. Возьмем частную производную получаем физический смысл , F S S . Отсюда T , ni качественной характеристики поверхности. Поверхностное натяжение - это изменение свободной энергии поверхностного слоя, приходящееся на единицу увеличения поверхности. Чтобы увеличить поверхность, надо совершить работу. Отсюда вытекает второе определение: поверхностное натяжение это обратимая изотермическая работа образования единицы поверхности, которая межмолекулярного затрачивается взаимодействия и на преодоление переходит в сил свободную поверхностную энергию. Объединенное уравнение первого и второго начал термодинамики может быть записано и относительно других характеристических функций, а именно, энергии Гиббса G , внутренней энергии U , энтальпии H . При соответствующих постоянных параметрах получим: 47 Это - уравнение для закрытой гетерогенной системы с плоской Эту разность, положительную или отрицательную, относят к учитывается разделяющей поверхности. При таком рассмотрении поверхность вещественный обмен, т.к. число молекул в системе может изменяться, характеризуется избыточными термодинамическими параметрами, и уравнение принимает вид: отражающими проявление поверхностной энергии. В соответствии с границей раздела. Для открытой системы dF ds S dT p dV i dni методом избыточных величин энергия Гиббса двухфазной системы (2.4) Это уравнение отличается от уравнения для гомогенной системы членом ds , обозначающим работу образования поверхности. Из равна сумме энергий Гиббса отдельных фаз и поверхностной энергии Гиббса s , которая является избыточной. этого уравнения видно, что с увеличением поверхности увеличивается свободная поверхностная энергия. При увеличении числа компонентов также происходит увеличение свободной поверхностной энергии. 2.7. Уравнение Гиббса для плоского поверхностного Рис. 2.7. Энергия Гиббса двухфазной системы с разделяющей поверхностью. слоя G G G s Плоским поверхностным слоем называется такой слой, толщина которого много меньше радиуса кривизны, т. е. система отвечает условию: Избыток числа молей компонентов на поверхности R . ni ni ni Vi ni Vi ni S Для всей системы изменение свободной энергии определяется выражением dF dF dF dF S . полученному для системы с Согласно плоской выражению, границей раздела dF ds S dT p dV i dni . В соответствии с методом избыточных величин Гиббса поверхностном слое равно изменение свободной энергии в dF S dF dF dF . Для каждой объемной фазы справедливо выражение dF S dT p dV i dni dF S dT p dV i dni (2.5) (2.6) Рис. 2.8. Изменение плотности свободной энергии на межфазной границе в реальной системе ( а ) и в модели Гиббса ( б ). Таким образом, согласно методу Гиббса свойства реальной системы отождествляются со свойствами идеализированной системы, 46 43 состоящей из двух фаз с разделяющей поверхностью, в которой зообразной фазы сосредоточены величина поверхности на dS . избытки термодинамических свойств. Изменение плотности свободной энергии на границе фаз в реальной и идеальной и жидкой фазы объем увеличился на dV , а системе показано на рис. 2.8 Метод Гиббса имеет существенные недостатки. Он применим только к гетерогенным системам, состоящим из двух жидких фаз или жидкой и газообразной фазы. Проведение сравнения реальной и идеализированной систем и избыточных функций приводит Рис. 2.9. К выводу фундаментального уравнения Гиббса. к формальным затруднениям. Избыточные параметры зависят от dA p dV ds . Поскольку При этом совершается работа положения разделяющей поверхности. Наконец, этот метод не увеличение объема происходит самопроизвольно, первый член этого позволяет рассмотреть свойства поверхностного слоя. выражения От этих методом недостатков слоев свободен конечной второй толщины. метод, Согласно называемый этому методу определяются не избыточные, а полные значения термодинамических параметров в поверхностном слое. Избыток энергии Гиббса в системе определяется суммой избытков энергии Гиббса в каждой фазе и в поверхностном слое: G G G G смысл. поверхностного слоя Однако, вследствие теплового движения. системой Увеличению работу, совершенную над системой вследствие притока тепла извне. Согласно первому закону dQ dU dA dU p dV ds . при Согласно установлении термодинамики второму равновесия закону dQ T dS . Объединим уравнения первого и второго закона термодинамики при определять малой толщину величины и неопределенности этой характеристики. 2.6. Фундаментальное уравнение Гиббса для свободной энергии гетерогенной системы с плоской границей раздела фаз Пусть в гетерогенной системе, не способной к обмену ком- установлении равновесия. Запишем T dS dU p dV ds . dU T dS p dV ds (2.2) Перейдем от внутренней энергии к свободной энергии, т.е. заменим U на F : U F T S dU dF T dS S dT (2.3) Объединим уравнения (2.2) и (2.3): dF T dS S dT T dS p dV ds dF ds S dT p dV понентами со средой, т. е. закрытой системе, состоящей из га44 совершенную поверхности система противится, поэтому второй член означает термодинамики трудно вследствие самопроизвольно работу, S Все величины, определяемые этим методом, имеют ясный физический означает 45