107 Лекция 12. КРИВИЗНА КРИВОЙ. 1. Понятие кривизны

Лекция 12. КРИВИЗНА КРИВОЙ.
1. Понятие кривизны кривой.
2. Вычисление кривизны кривой.
3. Радиус, круг и центр кривизны плоской кривой.
4. Эволюта и эвольвента плоской кривой.
1. Понятие кривизны кривой.
Одной из важных характеристик кривой является мера ее
изогнутости – кривизна.
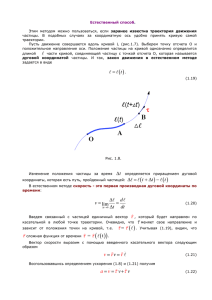
Пример. О двух плоских кривых ACB ⊂ Γ1 и ADB ⊂ Γ2
(рис.1) можно сказать, что кривая Γ2 более изогнута, чем Γ1 .
Отношение угла смежности дуги к ее длине называется сред∆ϕ
.
ней кривизной дуги: K cp =
∆l
Средняя кривизна характеризует среднюю изогнутость кривой на всей дуге. На отдельных участках кривой кривизна может
значительно отличаться от средней. Чтобы избежать такой неопределенности, вводится количественная мера изогнутости кривой в точке M . Эта характеристика основана на том, что чем
меньше дуга Γ (рис.2), тем лучше средняя кривизна характеризует изогнутость линии вблизи точки M .
О п р е д е л е н и е 1. Кривизной K линии Γ в точке M называется предел, к которому стремится средняя кривизна K cp
дуги MM 1 линии Γ при стремлении точки M 1 к точке M :
K = lim K cp = lim
M1 →M
∆l →0
∆ϕ
.
∆l
2. Вычисление кривизны кривой.
Векторное представление кривой. Пусть кривая Γ является
годографом дважды дифференцируемой векторной функции
r
действительного аргумента Γ = {r (t ) a ≤ t ≤ b} (рис.3).
Рис.1.
Однако для того, чтобы строго оценить степень изогнутости
плоской линии, необходимо ввести количественную характеристику ее изогнутости (кривизны).
Рассмотрим на кривой точки M и M 1 . Проведем в этих точках касательные к кривой. При переходе по кривой из точки M
в точку M 1 касательная поворачивается на угол ∆ϕ , который
называется углом смежности (рис.2).
Рис.3.
Рис.2.
107
108
∆ϕ
. Угол смежности ∆ϕ – угол
∆l →0 ∆l
r
r
r
r
r
между r ' (t ) и r ' (t + ∆t ) . Тогда вектор r ' (t + ∆t ) = r ' (t ) + ∆r ' (t ) .
r
r
Из векторного произведения векторов r ' (t ) и r ' (t + ∆t ) , находим:
r r r
r '×(r '+ ∆r ')
sin∆ϕ = r r r .
r ' r '+ ∆r '
r r
Поскольку r '×r ' = 0 , то в силу свойств векторного произведения имеем
r r
r '×∆r '
sin∆ϕ = r r r .
r ' r '+ ∆r '
Кривизна кривой K = lim
При ∆t → 0 имеем ∆l → 0 и ∆ϕ → 0 . Также ∆ϕ ~ sin∆ϕ , так
sin∆ϕ
как lim
=1.
∆ϕ →0 ∆ϕ
Следовательно, кривизна
r r
r '×∆r '
∆ϕ
sin∆ϕ
= lim
= lim r r r
=
K = lim
∆l → 0 ∆l
∆l → 0
∆t → 0 r ' r '+ ∆r ' ⋅ ∆l
∆l
r
r ∆r '
r '×
∆t
= lim
.
∆t →0 r r
r ∆l
r ' r '+ ∆r ' ⋅
∆t
r
r
Если ∆t → 0 , то r ' (t + ∆t ) → r ' (t ) и ∆l ≈ ∆r ; тогда
r r
r '×r ' '
K = r3 .
r'
Тогда вектор-функция имеет вид
r
r
r
r
r (t ) = x(t ) ⋅ i + y (t ) ⋅ j + z (t ) ⋅ k .
Отсюда
r
r
r
r
r ' (t ) = x' (t )i + y ' (t ) j + z ' (t )k ,
r
r ' = x'2 + y '2 + z '2 ,
r
r
r
r
r ' ' (t ) = x' ' (t )i + y ' ' (t ) j + z ' ' (t )k .
r
r r
i
j k
r r
Тогда r '×r ' ' = x' y ' z ' и
x' ' y ' ' z ' '
(
) (
) (
)
2
2
2
r r
r '×r ' ' = y ' z '' − y '' z ' + z ' x '' − z '' x ' + x ' y '' − x '' y ' .
Подставляя в формулу для вычисления кривизны, получим
искомое выражение.
В декартовых координатах. Если кривая Γ , задана уравнением y = f (x ) , то формулу для вычисления ее кривизны можно
получить из формулы вычисления кривизны, положив в ней
t = x , z = 0.
Действительно, уравнение линии Γ можно записать в параметрическом виде:
y = f (x ),⎫
⎬
t = x. ⎭
2
r r
r
Тогда r '×r ' ' = 0 + 0 + 1 ⋅ y '' − 0 = y '' и r ' = 1 + y '2 .
(
)
Значит,
K=
y ''
(1 + ( y') )
2 3/ 2
.
Данная формула используется для вычисления кривизны кривой Γ , если она является годографом дважды дифференцируемой векторной функции r (t ) .
В параметрическом виде. Пусть гладкая плоская кривая Γ
задана параметрическими уравнениями:
Γ = {x(t ); y (t ); z (t ) a ≤ t ≤ b}.
Пример. Вычислить кривизну кривой y = lnx в точке x = 1 .
1
1
Р е ш е н и е . Находим y ′ = , y ′′ = − 2 . Тогда кривизна криx
x
вой y = lnx в любой ее точке M с абсциссой x есть
109
110
−
K=
1
x2
1 ⎞
⎛
⎜1 + 2 ⎟
x ⎠
⎝
3/ 2
=
x
(1 + x )
2 3/ 2
.
В точке x = 1 имеем
K
x =1 =
1
2
=
3/ 2
2
.
4
3. Радиус, круг и центр кривизны плоской кривой.
Проведем к кривой Γ нормаль в точке M (x; y ) и отложим на
этой нормали в сторону вогнутости кривой отрезок MN = R
(рис.4), по величине обратный кривизне K :
1
R= .
K
R=
(x' + y' )
2
2 3/ 2
y '' x ' − y ' x ''
.
Если кривая Γ – годограф вектор-функции r = r (t ) , то:
r3
r'
R= r r .
r '×r ' '
4. Эволюта и эвольвента плоской кривой.
Из определения центра кривизны следует, что каждой точке
M кривой Γ , соответствует точка N – центр кривизны кривой
Γ ' в точке M .
О п р е д е л е н и е 2. Множество точек Γ' центров кривизны
линии Γ называется ее эволютой, а сама линия Γ по отношению к своей эволюте называется эвольвентой.
Выведем уравнение эволюты кривой Γ .
Векторное представление
r
r кривой. Пусть кривая Γ задана
r
уравнением r (t ) = x ⋅ i + y ⋅ j в плоскости Oxy . Пусть N (ξ ;η ) –
центр кривизны линии Γ в точке M (рис.5).
.
Рис.4
Отрезок MN называется радиусом кривизны, точка N –
центром кривизны, а круг с центром в точке N и радиусом R
– кругом кривизны кривой в точке M (x; y ) .
В случае, когда кривая Γ задана в декартовой системе координат Oxy уравнением y = f (x ) , то ее радиус кривизны находится по формуле:
R=
(1 + y′ )
2 3/ 2
y ′′
.
Если кривая Γ в плоскости Oxy задана параметрическими
уравнениями, то ее радиус кривизны определяется по формуле:
111
Рис.5.
Тогда для любой точки M (x; y )∈ Γ имеем ON = OM + MN .
r
r
r
r
Обозначим ON = r1 , OM = r , MN = R ⋅ n 0 , где n 0 – единичный
вектор нормали кривой Γ . Тогда
r r
r
r1 = r + Rn 0 .
Это уравнение называется векторным уравнением эволюты
кривой Γ .
112
r
В параметрическом виде. Запишем разложения векторов r1
r
r
r
r
r
r
r
r
и r по базису B = i , j : r1 = ξ ⋅ i + η ⋅ j и r = x ⋅ i + y ⋅ j . Найдем
r
вектор n 0 . Единичный вектор касательной к кривой Γ
r
r
r
r
r r ′(t ) x'⋅i + y′ ⋅ j
x'
y'
=
τ = r =
i+
j.
r ′(t )
x'2 + y '2
x'2 + y '2
x'2 + y '2
r
Продифференцируем равенство τ 2 = 1 по t . Имеем
r
r dτ
2τ =
= 0.
dt
r
r
r
r dτ
dτ
Отсюда
⊥ τ . Таким образом, вектор нормали n =
.
dt
dt
r
Найдем координаты вектора n :
'
'
r
⎞r
⎞r ⎛
r dτ ⎛⎜
x'
y'
⎜
⎟
⎟
n=
i+
=
j=
⎜ x'2 + y '2 ⎟
dt ⎜ x'2 + y '2 ⎟
⎝
⎠
⎝
⎠
x' y ' '+ y ' x' ' r
x' y ' '− y ' x' ' r
i + x'
j.
= − y'
2
2 3
2
2 3
x' + y '
x' + y '
r
r
r
x'
y'
j.
Тогда n 0 = m
i±
x'2 + y '2
x'2 + y '2
{ }
(
)
(
(
)
Γ является эвольвентой по отношению к кривой Γ' .
Ниже приведены свойства эволюты и эвольвенты, устанавливающие связь между ними
1. Нормаль к эвольвенте Γ является касательной к эволюте в
соответствующей точке.
2. Если на некотором участке эвольвенты радиус кривизны
изменяется монотонно, то приращение радиуса кривизны на
этом участке равно по абсолютной величине длине дуги соответствующего участка эволюты.
Пример. Найти эволюту эллипса
Γ = { x = a cos t ; y = b sin t ; 0 ≤ t ≤ 2π } .
Р е ш е н и е . Имеем
x' = −a sin t ,
y '= b cos t ,
x '' = −a cos t ,
y '' = −b sin t .
Подставляя в формулы для эволюты, получим
a2 − b2
b2 − a2
ξ=
cos 3 t , η =
sin 3 t .
a
b
Данные уравнения являются параметрическими уравнениями
астроиды (рис.6).
)
3/ 2
r
x'2 + y '2
в векторное уравнение эвоПодставим n 0 и R =
y ' ' x'− y ' x' '
r
r
r
люты r1 (t ) = r (t ) + R ⋅ n 0 :
r
r
r
r
x'2 + y '2 r
x'2 + y '2 r
ξ ⋅ i + η ⋅ j = x ⋅ i + y ⋅ j − y'
j.
i + x'
x' y ' '− y ' x' '
y ' ' x'− y ' x' '
r
r
Приравнивая коэффициенты при i и j в левой и правой частях выражения, получим:
x'2 + y '2
x'2 + y '2
ξ = x − y'
,
η = y + x'
.
y ' ' x'− y ' x' '
y ' ' x'− y ' x' '
Данные формулы являются параметрическими уравнениями
эволюты Γ' кривой Γ = {x(t ); y (t ); z = 0 0 ≤ t ≤ T }. Сама же кривая
113
Рис.6.
Вопросы для самоконтроля
1. Дайте определение кривизны и радиуса кривизны кривой.
2. Как вычисляется кривизна в случаях векторного, параметрического представления кривой.
3. Дайте определение радиуса, круга и центра кривизны плоской кривой.
4. Что называется эволютой и эвольвентой плоской кривой.
114