Аналитическое исследование нагрева твердых тел радиацией

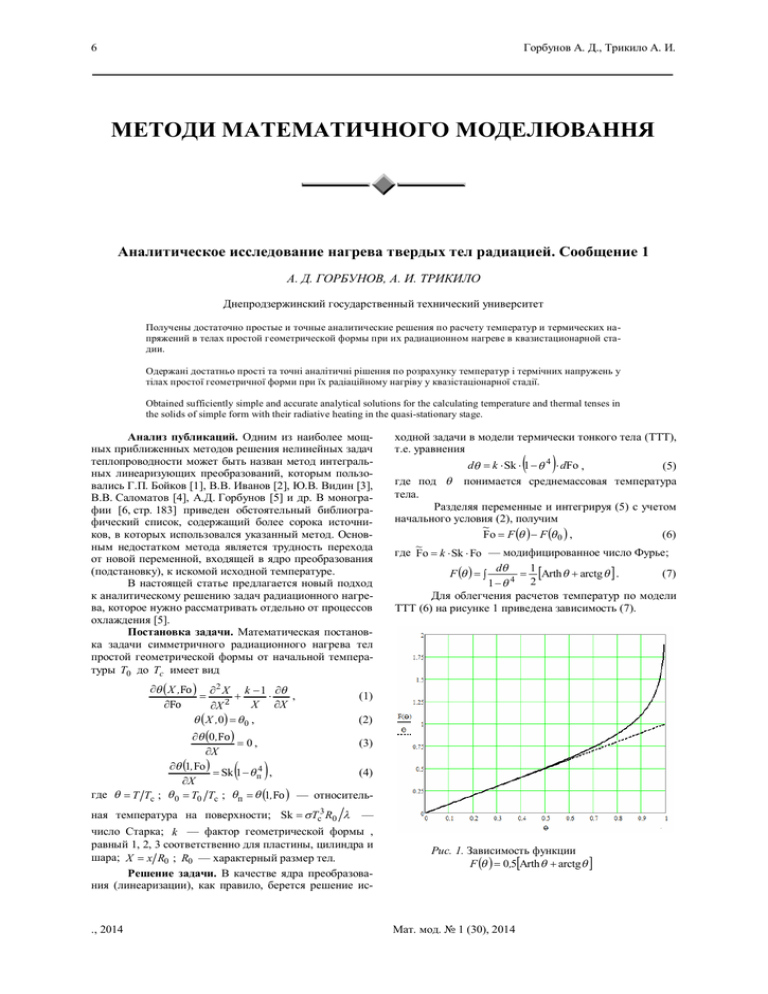
6
Горбунов А. Д., Трикило А. И.
МЕТОДИ МАТЕМАТИЧНОГО МОДЕЛЮВАННЯ
Аналитическое исследование нагрева твердых тел радиацией. Сообщение 1
А. Д. ГОРБУНОВ, А. И. ТРИКИЛО
Днепродзержинский государственный технический университет
Получены достаточно простые и точные аналитические решения по расчету температур и термических напряжений в телах простой геометрической формы при их радиационном нагреве в квазистационарной стадии.
Одержані достатньо прості та точні аналітичні рішення по розрахунку температур і термічних напружень у
тілах простої геометричної форми при їх радіаційному нагріву у квазістаціонарної стадії.
Obtained sufficiently simple and accurate analytical solutions for the calculating temperature and thermal tenses in
the solids of simple form with their radiative heating in the quasi-stationary stage.
Анализ публикаций. Одним из наиболее мощных приближенных методов решения нелинейных задач
теплопроводности может быть назван метод интегральных линеаризующих преобразований, которым пользовались Г.П. Бойков [1], В.В. Иванов [2], Ю.В. Видин [3],
В.В. Саломатов [4], А.Д. Горбунов [5] и др. В монографии [6, стр. 183] приведен обстоятельный библиографический список, содержащий более сорока источников, в которых использовался указанный метод. Основным недостатком метода является трудность перехода
от новой переменной, входящей в ядро преобразования
(подстановку), к искомой исходной температуре.
В настоящей статье предлагается новый подход
к аналитическому решению задач радиационного нагрева, которое нужно рассматривать отдельно от процессов
охлаждения [5].
Постановка задачи. Математическая постановка задачи симметричного радиационного нагрева тел
простой геометрической формы от начальной температуры T0 до Tc имеет вид
¶q ( X ,Fo) ¶ 2 X k - 1 ¶q
=
+
×
,
¶Fo
X ¶X
¶X 2
q ( X , 0) = q 0 ,
ходной задачи в модели термически тонкого тела (ТТТ),
т.е. уравнения
(
)
dq = k × Sk × 1 - q 4 × dFo ,
(5)
понимается среднемассовая температура
где под q
тела.
Разделяя переменные и интегрируя (5) с учетом
начального условия (2), получим
~
Fo = F (q ) - F (q 0 ) ,
(6)
~
где Fo = k × Sk × Fo — модифицированное число Фурье;
dq
1
F (q ) = ò
(7)
= [Arth q + arctg q ] .
1-q 4 2
Для облегчения расчетов температур по модели
ТТТ (6) на рисунке 1 приведена зависимость (7).
(1)
(2)
¶q (0 ,Fo)
= 0,
(3)
¶X
¶q (1, Fo )
(4)
= Sk 1 - q п4 ,
¶X
где q = T Tc ; q 0 = T0 Tc ; qп = q (1,Fo ) — относитель-
(
)
ная температура на поверхности; Sk = sTc3 R0 l
—
число Старка; k — фактор геометрической формы ,
равный 1, 2, 3 соответственно для пластины, цилиндра и
шара; X = x R0 ; R0 — характерный размер тел.
Решение задачи. В качестве ядра преобразования (линеаризации), как правило, берется решение ис-
., 2014
Рис. 1. Зависимость функции
F (q ) = 0,5[Arth q + arctg q ]
Мат. мод. № 1 (30), 2014
6
Горбунов А. Д., Трикило А. И.
Применяя к системе уравнений (1)...(4) следующую, линеаризующую граничное условие (4), подстановку
W ( X ,Fo ) = exp[- F (q ( X ,Fo ))] ,
(8)
получим постановку задачи в новых переменных
¶W ( X ,Fo) ¶ 2W ( X ,Fo) k - 1 ¶W
=
+
+ y ( X ,Fo ) , (9)
¶Fo
X ¶X
¶X 2
W ( X ,0 ) = exp (- F (q 0 )) = W0 ,
(10)
¶W (0 ,Fo)
=0,
¶X
¶W (1,Fo)
= -Sk × W (1,Fo) ,
¶X
y ( X ,Fo) =
(11)
(12)
(4q ( X ,Fo) - 1) × æç ¶W (X ,Fo) ö÷
3
2
.
(13)
W ( X ,Fo)
¶X
ø
è
Комплекс (13), имитирующий сток тепла переменной по величине и знаку интенсивности, содержит в
себе все нелинейные особенности исходной задачи
(1)...(4). В первом приближении искомая температура
W ( X ,Fo ) может быть найдена из решения системы
(9)...(12) при y ( X ,Fo) = 0 . Согласно [8] будем иметь
¥
W1 ( X ,Fo) = W0 × å Pn (mn ) × U n ( X ) × e - m n Fo ,
n =1
2
(14)
2Sk
— тепловая амплитуда;
Sk (Sk + 2 - k ) + m n2
— координатная функция, например, для пла-
где Pn (m n ) =
U n (X )
При умеренных, средних температурах можно
рекомендовать линейную зависимость, полученную в
[4]:
q (W ) = 1,4 - 1,47W .
(20)
На рис. 2 наглядно видно, что зависимость (8)
лежит между тремя кривыми (18), (20) и (19). Таким
образом, искомый переход от W к q имеет вид:
ì- lnW ,
если 0 ,6 £ W £ 1
ïï
q (W ) = í1,4 - 1,47 ×W , если 1 3 < W < 0 ,6
ï
ïî1 - C2W 4 , при 0 £ W £ 1 3 .
Следует отметить, что кривая (8) имеет перегиб
в точке q p = 4 -1 3 = 0 ,63 и эта точка замечательна тем,
что в ней обращается в ноль нелинейный комплекс (13).
В связи со сказанным решение (6) также упростится. Для начальной стадии нагрева
~
q (Fo) = q 0 + Fo , q 0 £ q £ 0 ,6
(21)
и конечной стадии
~
q (Fo ) = 1 - (1 - q 0 ) × e -4 Fo
(22)
при 0 ,6 < q £ 1 .
Заметим, что зависимость (22) хорошо согласуется с известным уравнением
(23)
q (Fo ) = 1 - (1 - q 0 )exp (- k × Bi × Fo )
в случае конвективного нагрева ТТТ, где Bi = aR0 l —
число Био.
стины: U n ( X ) = cosm n X cos mn ; m n — корни характеристического уравнения
ctgm n = m n Sk .
(15)
После определения W ( X ,Fo ) следует сделать
переход с помощью уравнения (8) от W к исходной
температуре q , однако из-за сложности функции F (q )
сделать это весьма затруднительно. Для упрощения
этого перехода поступим следующим образом.
Сначала воспользуемся разложением функции
F (q ) в ряд при q < 1
æ q 5 q 9 q 13
ö
F (q ) = q çç1 +
+
+
+ ...÷÷ .
(16)
5
9
13
è
ø
При q £ 0,6 можно ограничиться одним членом
ряда (16) и получить
F (q ) = q .
(17)
На рис. 1 для наглядности нанесена прямая (17).
Тогда из уравнения (8) получим
W = e -q или q = - lnW .
(18)
В конечной стадии процесса нагрева, когда температуры q близки к 1 положим в уравнении (7)
p
1 1+ q 1
2
Arthq = ln
» ln
и arctgq » arctg1 = .
2 1 -q 2 1 - q
4
1
2
p
Тогда F (q ) » ln
+
и окончательно со4 1-q 8
гласно (8) будем иметь
q (W ) = 1 - C2 × W 4 ,
p 2
где C2 = 2e
= 9 ,62095476 .
ÓПолисский Ю. Д., 2014
(19)
Рис. 2. Зависимости построенные по уравнениям
w — (8), w1 — (18), w2 — (20) и w3 — (19)
Зная первое приближение функции W можно, с
помощью уравнения (14) найти нелинейный комплекс
(13) в первом приближении y 1( X ,Fo ) , а затем второе
приближение согласно [4], например, для пластины
W2 ( X ,Fo) = W1 ( X ,Fo) +
(
)
Fo1
é¥
+ W0 × ê å Pn (m n ) ×U n ( X ) ò òy 1 X ,Fo * × cos m n X ´ (24)
00
ën =1
[
(
)]
]
´ exp - m n2 × Fo - Fo* dFo* × dX .
Второе приближение служит основой для расчета третьего и т.д. приближения до получения решения с
необходимой точностью.
Для определения погрешности метода и его сходимости в [4] было произведено сравнение результатов
Мат. мод. № 1 (30), 2014
Аналитическое исследование нагрева твердых тел радиацией. Сообщение 1
численного расчета исходной системы (1)…(4) на ЭВМ
с данными расчета по предложенным уравнениям (14),
(24) и (8). Проведенный анализ позволил установить,
что погрешность в расчете q ( X , Fo ) по предлагаемому
методу не превышает 5 % во всех точках тела для
Sk £ 0 ,5 если ограничиться первым приближением, для
0 ,5 £ Sk £ 2 — вторым и для 2 £ Sk £ 5 — третьим
приближением. Максимальная погрешность приходилась на расчет температур в центральных точках тела.
Поскольку число Фурье было Fo > 0,3 , что соответствует регулярному (квазистационарному) режиму
нагрева, ограничимся в уравнении (14) одним первым
членом ряда.
Тогда температура на поверхности
Wп (Fo ) = W0 × P1 × e - m1 Fo ,
среднемассовая
2
(25)
Wср (Fo) = m × Wп (Fo)
(26)
(27)
где m = (1 + a ) — коэффициент термической массивности тела; a = Sk (k + 2 ) ; H k — амплитуда для центральных точек тела, например, согласно [8] в случае
пластины H1 = 1 cosm1 = 1 + mSk ; первый корень характеристического уравнения (15):
m1 = D g ;
(
(28)
)
D = kSk m ; g = 1 + 1 + 4 r 2 ;
[
]
r = D k (k + 2 ) (k + 4 ) .
На начальной стадии нагрева, когда q < 0,6 ,
можно использовать (18) и тогда уравнения (25)…(27)
для расчета температур на поверхности q п , среднемассовой q cр и в центре тела q ц значительно упрощаются
2
2
до следующей линейной зависимости от времени:
q п (Fo ) = C p + m 2 Fo , q cp (Fo ) = Ccp + m 2 Fo
q ц (Fo ) = Cc + m 2 Fo ,
где
Заметим, что согласно (28) в уравнениях
~
(25)…(31) можно заменить m 2 Fo на Fo (mg ) . Аналогичные зависимости были получены ранее, см. уравнения (21) и (22), для модели ТТТ. Кроме того решения
(30) и (31) по нашему мнению соответствуют двум упорядоченным тепловым режимам нагрева тел радиацией,
выявленных Г.П. Бойковым [1] полвека назад.
На самой начальной стадии нагрева, при малых
числах Фурье ( Fo < 0 ,1 ), расчет температур можно порекомендовать производить по методике, изложенной в
[9].
В подавляющем большинстве работ, посвященным радиационному теплообмену [2...7] и др. отсутствуют формулы по определению среднемассовой температуры, без знания которой невозможно рассчитать
термические напряжения. В работе [8] показано, что
осевые термические напряжения составляют:
на поверхности
s п (t ) = S1 Tср (t ) - Tп (t ) , Па
(32)
и в центре
и в центральных точках
Wц (Fo) = H k × Wп (Fo) ,
C p = -ln(W0 × P ) » q0 - lnP ;
и
(29)
Ccp = C p - ln m ;
Cц = C p - lnH k .
Вместо трех уравнений (29) можно записать одну обобщенную формулу
q j (Fo ) = C j + m 2 Fo ,
(30)
s~ц (Fo) = qср (Fo) - qц (Fo) ,
(35)
~
~
где s = s s 01 ; 0 £ s £ 1 ; s 01 = S1 × Tc — максимально
возможные
термические
напряжения,
Па;
=
S1 bE (1 - n ) ; b — линейный коэффициент термического расширения, 1/К; E — модуль упругости Юнга,
Па; n — коэффициент Пуассона.
Выводы
1. С помощью подстановки, линеаризирующей
граничное условие, получены приближенные аналитические решения по расчету температур и термических
напряжений в телах простой геометрической формы
при их радиационном нагреве.
2. Сопоставление с численными решениями
температур поверхности и центра пластины свидетельствует о достаточной для инженерных расчетов точности.
3. Получены приближенные аналитические
формулы для расчета полей температур, подтверждающие существование двух упорядоченных тепловых режимов при лучистом нагреве твердых тел, выявленных
ранее Бойковым Г.П.
В конечной стадии нагрева ( 0 ,6 < q £ 1 ) с учетом
зависимости (19) будем иметь
2.
ЛИТЕРАТУРА
)
q j (Fo ) = 1 - C3 j exp - 4 m Fo ,
где C3 j
ì P 4 , если j = 1
ïï
= C2 × W04 × ím 4 , если j = 2
ï 4
H , если j = 3.
îï k
(33)
и в центре
1.
(
[
]
s ц (t ) = S1 [Tср (t ) - Tц (t )] , Па.
Приведя последние уравнения к безразмерному
виду, получим относительные термические напряжения
на поверхности s~п (Fo) = q ср (Fo) - qп (Fo )
(34)
ì1 - температур а поверхност и,
ï
где j = í2 - среднемасс овая,
ï3 - в центре ттела
î
2
7
(31)
3.
4.
Бойков Г. П. Прогрев тел под действием лучистого
тепла / Изв. ТПИ. — 1957. Т. 89, 33.
Иванов В. В. Расчет радиационного охлаждения
тепловыделяющих элементов // ИФЖ. — 1966. —
Т. ХІ. — № 4. — С. 542—544.
Видин Ю.В., Иванов В.В. Расчет температурных
полей в твердых телах, нагреваемых конвекцией и
радиацией одновременно. — Красноярск: КПИ,
1971. — 144 с.
Саломатов В. В., Горбунов А. Д. Аналитическое
исследование прогрева твердых тел радиаци-
6
5.
6.
7.
Горбунов А. Д., Трикило А. И.
ей // Изв.
вузов.
Энергетика. — 1969. № 3. —
С. 124—127.
Горбунов А.Д. Аналитическое исследование охлаждения твердых тел радиацией // Математичне моделювання. — Днепродзержинск: ДГТУ, 2013,
1(28). — С. 22—27.
Коздоба Л.А. Методы решения нелинейных задач
теплопроводности. — М.: Наука, 1975. — 228 с.
Саломатов В. В. К расчету радиационного охлаждения твердых тел // ИФЖ. — 1969. — Т. 17. —
№ 1. — С. 127—134.
8.
9.
Горбунов А. Д. К аналитическому расчету термических напряжений при конвективном нагреве тел
простой формы // Математичне моделювання. —
Днепродзержинск : ДГТУ, 2012.
№
1(26). —
С. 39—45.
Горбунов А. Д. Аналитический расчет процессов
радиационного нагрева (охлаждения) тел на начальной стадии // Математичне моделювання —
Днепродзержинск : ДГТУ,
2012, № 2(27). —
С. 90—94.
пост.26.12.13
ÓПолисский Ю. Д., 2014
Мат. мод. № 1 (30), 2014