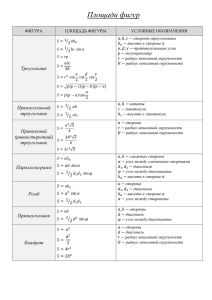
Формулы для площадей четырехугольников
реклама
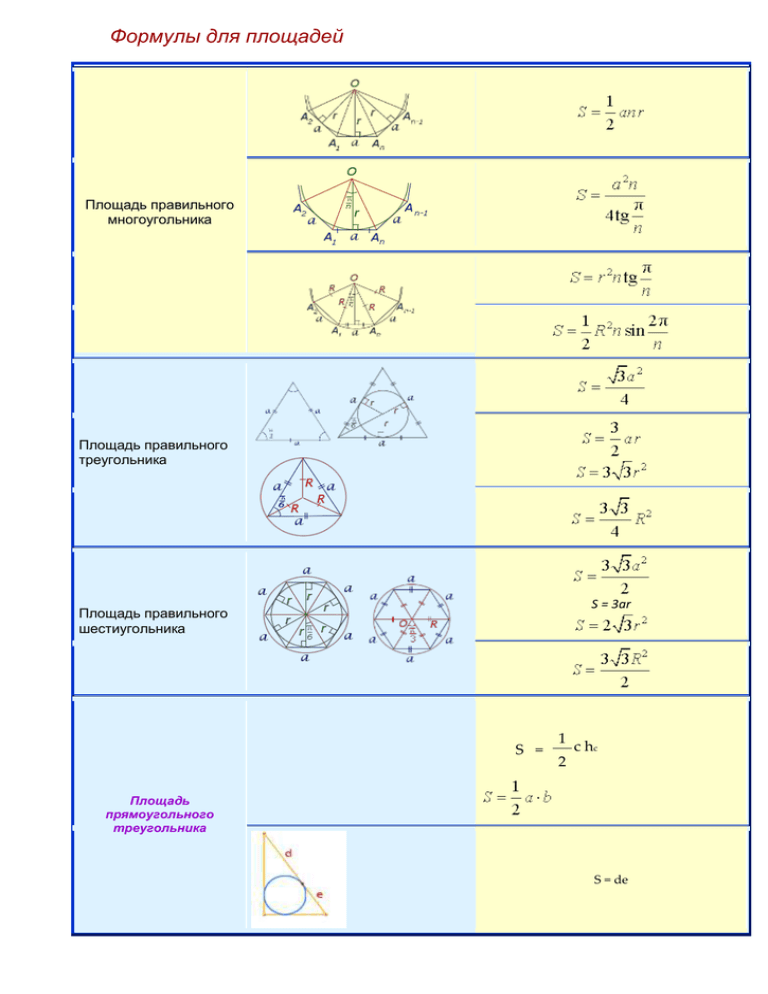
Формулы для площадей Площадь правильного многоугольника Площадь правильного треугольника S = 3ar Площадь правильного шестиугольника S = 1 с hc 2 Площадь прямоугольного треугольника S = de a – любая сторона, ha – высота, опущенная на эту сторону a и b – две любые стороны, С – угол между ними . a, b, c – стороны, p – полупериметр, формулу называют«Формула Герона» a – любая сторона, B, С – прилежащие к ней углы Площадь произвольного треугольника a, b, c – стороны, r – радиус вписанной окружности, p – полупериметр a, b, c – стороны, R – радиус описанной окружности S = 2R2 sin A sin B sin C A, B, С – углы, R – радиус описанной окружности a – любая сторона, ha – высота, опущенная на эту сторону Отношение площадей подобных треугольников равно квадрату коэффициента подобия Формулы для площадей четырехугольников Четырехугольник Рисунок Формула площади S = ab Обозначения a и b – смежные стороны d – диагональ, φ – любой из четырёх углов междудиагоналями Прямоугольник S = 2R2 sin φ S = a ha R– радиус описанной окружности, φ – любой из четырёх углов между диагоналями a – сторона, ha – высота, опущенная на эту сторону Параллелограмм S = ab sin φ a и b – смежные стороны, φ – угол между ними d1 и d2 – диагонали, φ – любой из четырёх углов между ними S = a2 a – сторона квадрата S = 4r2 r – радиус вписанной окружности Квадрат d – диагональ квадрата S = 2R2 Получается из верхней формулы подстановкой d = 2R R – радиус описанной окружности a – сторона, ha – S = a ha высота, опущенная на эту сторону S = a2 sin φ a – сторона, φ – любой из четырёх углов ромба Ромб d1 и d2 – диагонали S = 2ar a – сторона, r – радиус вписанной окружности r – радиус вписанной окружности, φ – любой из четырёх углов ромба a и b – основания, h – высота m – средняя линия, h – высота S=mh Трапеция d1 и d2 – диагонали, φ – любой из четырёх углов между ними a и b – основания, cи d – боковые стороны d1 и d2 – диагонали, Произвольный выпуклый четырёхугольник φ – любой из четырёх углов между ними , Вписанный четырёхугольник a, b, c, d – длины сторон четырёхугольника, p – полупериметр, формулу называют«Формула Брахмагупты» Формулы для площади круга и его частей Числовая характеристика Рисунок Формула , Площадь круга где R – радиус круга, D – диаметр круга , если величина угла α выражена в радианах Площадь сектора , если величина угла α выражена в градусах , если величина угла α выражена в радианах Площадь сегмента , если величина угла α выражена в градусах Формулы для длины окружности и её дуг Числовая характеристика Длина окружности Рисунок Формула C = 2πR = π D, где R – радиус круга, D – диаметр круга L(α) = αR, если величина угла α выражена в радианах Длина дуги , если величина угла α выражена в градусах