Гл6. Основы массопередачи. Основные зависимости и

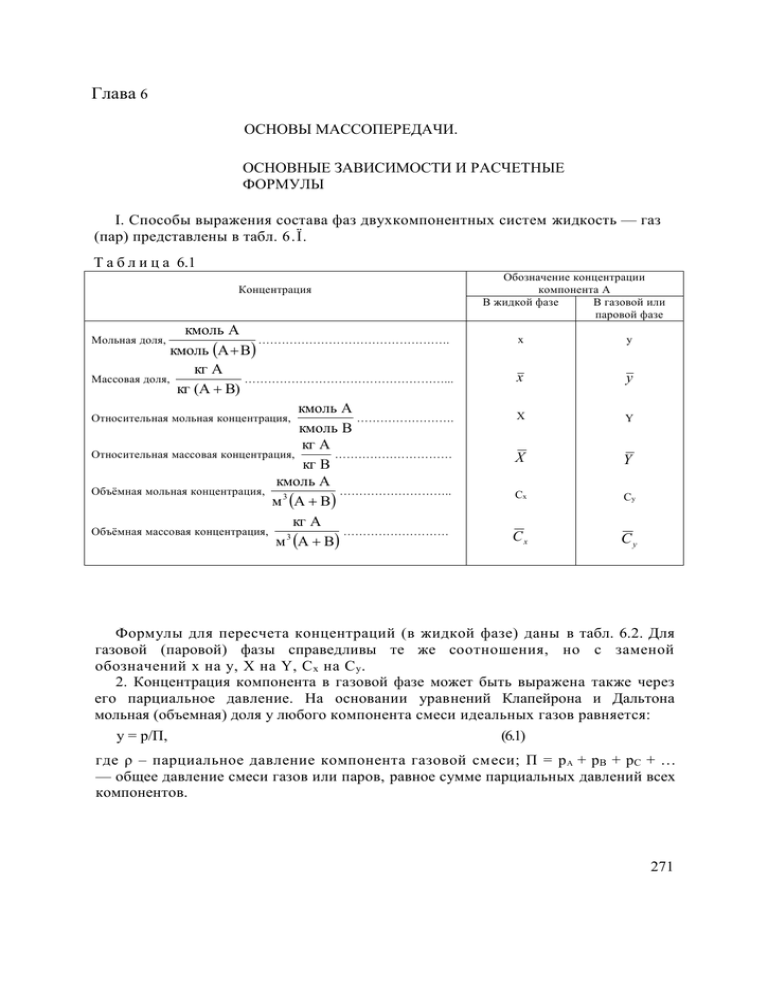
Глава 6
ОСНОВЫ МАССОПЕРЕДАЧИ.
ОСНОВНЫЕ ЗАВИСИМОСТИ И РАСЧЕТНЫЕ
ФОРМУЛЫ
I. Способы выражения состава фаз двухкомпонентных систем жидкость — газ
(пар) представлены в табл. 6.Ϊ.
Т а б л и ц а 6.1
Концентрация
кмоль А
………………………………………….
кмоль А  B
кг А
Массовая доля,
……………………………………………...
кг (А  В)
кмоль А
Относительная мольная концентрация,
…………………….
кмоль В
кг А
Относительная массовая концентрация,
…………………………
кг В
кмоль А
Объёмная мольная концентрация,
………………………..
м 3 А  В
кг А
Объёмная массовая концентрация,
………………………
3
м А  В
Мольная доля,
Обозначение концентрации
компонента А
В жидкой фазе
В газовой или
паровой фазе
x
y
x
y
X
Y
X
Y
Сx
Cy
Сx
Cy
Формулы для пересчета концентраций (в жидкой фазе) даны в табл. 6.2. Для
газовой (паровой) фазы справедливы те же соотношения, но с заменой
обозначений x на у, X на Y, С х на С у .
2. Концентрация компонента в газовой фазе может быть выражена также через
его парциальное давление. На основании уравнений Клапейрона и Дальтона
мольная (объемная) доля у любого компонента смеси идеальных газов равняется:
y = p/П,
(6.1)
где ρ – парциальное давление компонента газовой смеси; П = p А + pB + рC + …
— общее давление смеси газов или паров, равное сумме парциальных давлений всех
компонентов.
271
Выражен
ие
концентр
ации
компонен
та А
x
x
–
x
x M ср
МА
или
X
X
X
1 X
MBX
MBX  MA
M Ax
–
M см
C x M см

или
Сx M B
  M B  M A 
x/MA
x
1 x

MA MB
x
Cx
MAX
MAX  MB
X
1 X
M AC x

Cx
C x M см
или
M A
Сx M B
M A  C x ( M B  M A )
Cx

X
x
1 x
xM B
M A 1  x 
–
MBX
MA
M BCx
  M AC x
M BCx
M A   C x 
X
M Ax
M B 1  x 
x
1 x
MAX
MB
–
M AC x
  M AC x
Cx
  Cx
Cx
x
x
MA
X
X
MAX  MB
M A X  1
–
Cx
MA
M A X
MAX  MB
X
M AC x
–
M см
Cx
M A x
M см
x
X 1
Таблица 6.2
MA, MB, Mср – мольные массы компонентов и смеси, кг/кмоль; Мсм = МА х + МВ + (1 – х); ρ –
плотность смеси , кг/м3. Для смеси идеальных газов:
ПT0
ρ
П


M см RT 22.5П 0 Т
3. Законы межфазного равновесия для идеальных растворов.
а) Закон Генри:
р* = Ех
(6.2 )
где р* – парциальное давление компонента в газовой фазе над равновесной с газом
жидкостью; х – мольная доля компонента в жидкости; Ε – коэффициент Генри,
зависящий от температуры и от природы газа и жидкости.
Подставляя в уравнение (6.2) значение р* = у*П по уравнению (6.1), получаем:

y = mx
(6.3)
где у* – мольная доля компонента в газовой фазе, равновесной с жидкостью; m = Е/П –
безразмерный коэффициент (коэффициент распределения), постоянный для данной
системы газ – жидкость при t = const и Π = const.
Если, применительно к двухфазной трехкомпонентной системе (газовая фаза: А + В,
жидкая фаза: А + С), подставить в уравнение равновесия (6.3) значения х y  и для
компонента А, выраженные через его относительные концентрации X и Y  ,
X и Y (табл. 6.2), получим:
Y
X
m
(6.5)
M
MA

A
Y 
X
MB
MB
где МА – мольная масса распределенного между фазами компонента А; Мв – то же
второго компонента бинарной газовой смеси;
4
Aic — то же второго компонента бянарной жидкой смеси.
При малых концентрациях распределенного компонента в газе и в жидкости, когда
Y*<1 и X <1, в знаменателях уравнения (6.4) величинами Y* и X можно пренебречь, и
оно получает вид:
Y* = mx
(6.6)
M
M
Аналогично при Y  << A и X << A из уравнения (6.5) получим:
MB
MB
Y
X
m

1 X
1 Y
(6.4)
MC
(6.6а)
X
MB
б) Закон Рауля:
р* = Рх
(6.7)
где р* – парциальное давление компонента в парогазовой смеси над жидкостью в
условиях равновесия; Р – давление насыщен273
ного пара чистого компонента – однозначная функция температуры: Ρ = f(t); x –
мольная доля компонента в жидкости.
При подстановке в уравнение (6.7) значения р* = y*П из уравнения (6.1) получаем:
P
y  x
(6.8)
П
где у* – мольная доля компонента в парогазовой фазе, равновесной с жидкостью.
Для двух компонентной смеси, когда оба ее компонента следуют закону Рауля,
уравнение (6.8) приводится к виду:
x A
(6.9)
y A 
1    1x A
Здесь α = РA/РB — коэффициент относительной летучести; PA — давление
насыщенного пара более летучего (низкокипящего) компонента при той же
температуре; PB — давление насыщенного пара менее летучего (высококипящего)
компонента при той же температуре.
4. Многочисленные экспериментальные данные о равновесных составах жидкости и
пара для различных растворов имеются в справочнике [6.5].
5. Причиной (движущей силой) процесса массопередачи — перехода какого-либо
компонента из одной фазы в другую (например, из жидкой фазы Фx с мольной
концентрацией переходящего компонента к в газовую фазу Фу с мольной
концентрацией у) является неравновссность соприкасающихся фаз, их отклонение от
состояния динамического равновесия. В химической термодинамике устанавливается,
что величина этого отклонения, при равенстве температур и давлений фаз,
определяется разностью химических потенциалов переходящего компонента (μx – μy),
которая и является движущей силой процесса массопередачи. При равновесии фаз
потенциалы μx и μy равны.
Заменяя потенциал μx равным ему потенциалом равновесной газовой смеси μ y ,
получим для движущей силы процесса массопередачи выражение
μ x  μ y  μ y  μ y
Y m
Аналогично, заменяя потенциал µy равным ему потенциалом равновесной жидкой
фазы μ x ,получим:
μ x  μ y  μ x  μ x
Из последних равенств следует, что движущая сила процесса (μx – μy) может быть
выражена двумя способами: либо как разность химических потенциалов, взятых по
газовой фазе, либо как разность потенциалов, взятых по жидкой фазе. При этом необходимо помнить, что газовая фаза с потенциалом  y и концентрацией у*, так же как
и жидкая фаза с потенциалом μ x и концентрацией х*, – фазы гипотетические, в
реальном процессе массопередачи отсутствующие – см. рис. 6.1.
В технических расчетах применяют не химические потенциалы, а более простые,
легко определяемые величины – концентрации, с помощью которых также может
быть охарактеризовано отклонение фаз Фх и Фy от
состояния равновесия. Однако, в отличие от разности
химических потенциалов (μ x — μ y ), которая равна
нулю при равновесии фаз. разность концентраций (х– у),
в общем случае не равная нулю при равновесии , не
может служить мерой отклонения фаз от равновесного
состояния, т, е. движущей силой процесса
массопередачи. При технических расчетах движущую
силу процесса массопередачи – отклонение системы от
состояния равновесия – выражают поэтому как разность
концентраций (у*– у) или (х – х*). Так как
концентрации могут быть выражены в различных
единицах, то движущая сила процесса массопередачи
может иметь различные значения – см. пример 6.3.
6. В соответствии с двумя возможными способами
Рис. 6.1. Схема процесса
выражения движущей силы процесса массопередачи – массопередачи: ОО гра по газовой фазе (Δy = у* – у) или по жидкой фазе (∆x= х – ница раздела фаз.
х*) – уравнение массопередачи, аналогичное уравнению
теплопередачи, может быть написано в двух видах;
М = Ку ΔycpF
(6.10)
или М=Кx∆xсрF
(6.11)
Здесь Μ – расход компонента, переходящего из одной фазы в другую, кмоль/с;
F – площадь поверхности массопередачи, м 2 ; Ку — коэффициент массопередачи,
отнесенный к движущей силе Δy, выраженной через мольные доли компонента в
газовой фазе, кмоль/(м2·с) ; Кх – коэффициент массопередачи, отнесенный к
275
движущей силе Δx, выраженной через мольные доли компонента в жидкой фазе,
кмоль/(м2·с) ;∆ycр и ∆xср – соответствующие средние для всего процесса движущие
силы (см. ниже).
В последних уравнениях вместо мольных расходов и концентраций могут быть
массовые, а вместо ∆ycр могут быть , ∆Ycр, ∆Сycр и ∆рср; соответственно, вместо ∆хср
могут быть ∆Хср или ∆Схср .
7. При определенных допущениях (отсутствие диффузионного сопротивления при
переходе компонента через поверхность раздела фаз, существование равновесия на
этой поверхности, линейность уравнения равновесия у* = mх или у* = mх + b)
получаются следующие зависимости между коэффициентами массопередачи К у и Кх и
фазовыми коэффициентами массоотдачи β у и βx:
1
Кy 
1
m

βy
βx
Kx 
(6.12)
1
1
1

mβ y
βx
(6.13)
где m – тангенс угла наклона линии равновесия. Коэффициенты массоотдачи и
массопередачи выражены в кмоль/(м2·с).
Знаменатели последних уравнений представляют собою общее диффузионное
сопротивление, равное сумме диффузионных сопротивлений газовой и жидкой фаз.
Когда основное диффузионное сопротивление сосредоточено в газовой фазе, т. е. при
m
1
<<
βx
βy
Ky  βy
(6.14)
Когда основное диффузионное сопротивление сосредоточено в жидкой фазе, т. е. при
1
1
<<
βx
mβ y
(6.15)
Kx  βx
Из уравнений (6.12) и (6.13) следует, что
K y  K x /m
(6.16)
8. Основные диффузионные критерии подобия установившихся процессов
массоотдачи.
Диффузионный критерий Нуссельта:
βl
Nu'=
(6.17)
D
Диффузионный критерий Пекле:
ωl
Ре'=
(6.18)
D
Диффузионный критерий Прандтля;
Pe  υ
Pr  

(6.19)
Re D
276


 кмоль

кг
;
или
Здесь β – коэффициент массоотдачи, м/с 
кг 
 2 кмоль
2
м с 3 
 м с
м3
м 

l – характерный линейный размер, м; D – коэффициент молекулярной диффузии, м2/с; ω
– скорость газа или жидкости, м/с; ν – кинематический коэффициент вязкости, м2/с.
9. При отсутствии экспериментальных данных коэффициент диффузии
(молекулярной) газа А в газе В (или газа В в газе А) может быть вычислен по формуле:
DГ 
4.3  10 7 T
1
1
3
2
p(υ A3  υ B3 )
1
1

MA MB
(6.20)
где DГ – коэффициент диффузии, м2/с; Т – температура, К; p – давление (абсолютное),
кгс/см2; МА и МB – мольные массы газов А и В; vA и vB – мольные объемы газов А и В,
определяемые как сумма атомных объемов элементов, входящих в состав газа – см.
пример 6.6 (атомные объемы некоторых элементов и мольные объемы некоторых газов
приведены в табл. 6.3).
Таблица 6.3
Атомный объем, см3/атом
В…………………………….......................27.0
C…………………………….......................14.8
Cl…………………………………………..24.6
H…………………………………………….3.7
N в первичных аминах……........................10.5
N во вторичных аминах…………………..12.0
N с двумя насыщенными связями……….15.6
О с двумя насыщенными связями………...7.4
О в альдегидах и кетонах………………….7.4
О в сложных эфирах……………………….9.1
O в простых эфирах………………………..9.9
О в высших простых и сложных эфирах..11.0
О в кислотах………………………………12.0
О в соединениях с S,P,N…………………...8.3
S……………………………………………25.6
I…………………………………………….37.0
Мольный объем, см3/моль
Н2 …………………………………….14.3
О2 …………………………………….25.6
N2……………………………………..31.2
Воздух………………………………..29.9
СО……………………………………30.7
СО2…………………………………...34.0
SO2……………………………………44.8
NO…………………………………….23.6
N2O…………………………………...36.4
NH3…………………………………...25.8
H2O…………………………………...18.9
H2S……………………………………32.9
COS…………………………………...51.5
Cl2……………………………………..48.4
Br2……………………………………..53.2
I2……………………………………….71.5
Структурные постоянные*
Бензольное кольцо ..................–15
Нафталиновое кольцо.............–30
Антраценовое кольцо………–47,5
Как следует из формулы (6.20), если известно значение коэффициента диффузии D1
при температуре Т1 и давлении p1, то зна277
чение его D2 при температуре Т2 и давлении р2 можно найти из уравнения:
3
p T  2
D 2  D1 1  2 
(6.21)
p 2  T1 
10. Коэффициент диффузии в жидкости Dж при 20 °С можно вычислить по
приближенной формуле:
1  10 6
1
1
(6.22)
Dж 

2
1
1
MA MB

3
3 
AB μ  υ A  υ B 


где Dж – коэффициент диффузии, м2/с; μ – динамический коэффициент вязкости
жидкости, мПа·с; υА и υβ – мольные объемы растворенного вещества и растворителя;
МА и МB – мольные массы растворенного вещества и растворителя; А и В –
коэффициенты, зависящие от свойств растворенного вещества и растворителя.
Значения коэффициентов A для некоторых веществ, растворенных в воде:
для газов…………………………………………1
» этилового спирта...........................................1,24
» метилового спирта.........................................1,19
» уксусной кислоты...........................................1,27
Коэффициент В равен:
для воды…………………………………....................4,7
» этилового спирта……………...............................2,0
» метилового спирта……………………................2,0
» ацетона..................................................................1,15
» неассоциированных жидкостей…………….......1,0
Коэффициент диффузии газа в жидкости Dt (при температуре t) связан с
коэффициентом диффузии D20 (при температуре 20°С) следующей приближенной
зависимостью:
(6.23)
D t  D 20 1  bt  20
в которой температурный коэффициент b может быть определен по эмпирической
формуле:
0.2 μ
b
(6.24)
3 ρ
где μ – динамический коэффициент вязкости жидкости при 20°С, мПа·с; р – плотность
жидкости, кг/м3.
278
Коэффициент диффузии в разбавленных растворах может быть вычислен также
по формуле:
D ж  7.4  10
12
βM  12 T
(6.25)
μυ0.6
где Dж – коэффициент диффузии, м2/с; Μ – мольная масса растворителя; υ – мольный
объем диффундирующего вещества; Т – температура, К; μ – динамический коэффициент
вязкости растворителя, мПа·с; β – параметр, учитывающий ассоциацию молекул
растворителя и равный:
для
»
»
»
воды
метилового спирта
этилового спирта
бензола, эфира, гептана
2,6
1,9
1,5
1
11. Материальный баланс абсорбера (рис, 6.2).
При расчете абсорбера с нелетучим жидким поглотителем массовые (или мольные)
расходы поглотителя и инертного, нерастворяющегося в жидкости газа будут
постоянными по высоте абсорбера. Выражая концентрации поглощаемого компонента
в газе и жидкости в относительных массовых (или мольных) единицах, получим
уравнение материального баланса (в массовых единицах)·
M  GYн  Yв   LX н  X в 
(6.26)
где М – расход поглощаемого компонента, кг/с; G и L – расходы
инертного газа и жидкого поглотителя, кг/с; Yв , и Yв –
концентрации поглощаемого компонента в газе в низу и на_
верху абсорбера, кг/кг инертного газа; Х н и Х в – то же в
жидкости в низу и на верху абсорбера, кг/кг жидкого
поглотителя.
Рис, 6.2. Схема абсорбера.
В координатах Y  X уравнение (6.26), при постоянных G И L,
выражает отрезок прямой, проходящей через точки
BX н , Yн  и АX в , Yв  – см. рис. 6.3.
Уравнение этой прямой – рабочей линии;
L
Y  Yн  X  X н 
(6.27)
G
или
L
Y  Yв  X  X в 
(6.28)
G
где Y и X – переменные по высоте колонны концентрации поглощаемого компонента в
контактирующий неравновесных потоках газа и жидкости в данном сечении
абсорбера – рис. 6.2.
Расход жидкого поглотителя:
L = φ Lмин
(6.29)
где φ > 1 – коэффициент избытка поглотителя; Lмин – теоретически минимальный
расход поглотителя, определяемый графическим (см. рис. 6.3) или аналитическим
путем
M
X  Xв
Степенью поглощения
величина
L мин 
cп 
Yн  Yв Yн  Yв

Yн
Yн
Рис. 6.3. Рабочая и равновесная лилии
абсорбера:
AS – рабочая линия при расходе поглотителя L,
АС – рабочая линия при расходе поглотителя
Lмин;OC – равновесная линия
Y   f X 
(6.30)

н
(или
извлечения)
называется
(6.30a)
12. Средняя движущая сила в
абсорбере
с
непрерывным
контактом фаз.
В общем уравнении массопередачи
F
M
K y Yср
(6.31)
(где F – поверхность массопередачи в абсорбере, м2; М – расход поглощаемого
кг
компонента, кг/с; K y – коэффициент массопередачи,
) средняя
кг
2
м с
кг инертного газа
движущая сила Yср определяется следующим образом.
Если в пределах от X в до X н (рис. 6.3) линия равновесия прямая, то
Yн  Yв
(6.32)
Yср 
Yн
2.3lg
Yв
где Yн и Yв – концевые движущие силы; Yн  Yн  Yн – в низу абсорбера при
X  X н ; Y  Yв  Yв на верху абсорбера при X  X в
Когда отношение Yн и Yв находится в пределах
Yн
≤2
Yв
среднюю движущую силу в абсорбере можно рассчитывать по более простой
ΔYн  ΔYв
формуле: Yср 
(6.33)
2
Если же линия равновесия не прямая, то
0.5 ≤
Yср 
Yн  Yв
(6.34)
Yн
dY
Y Y  Y 
в
Величину интеграла в знаменателе последнего уравнения находят графическим
построенном или методом графического интегрирования. Другой метод расчета при
криволинейной линии равновесия: разбивают равновесную линию на участки,
принимаемые приближенно за отрезки прямых, и для каждого участка в отдельности
определяют среднюю движущую силу по уравнению (6.32) или (6.33).
При расчетах абсорберов движущую силу часто выражают в единицах давления –
см. пример 6 9.
13. Определение диаметра насадочного абсорбера.
Диаметр абсорбционной колонны D (в м) рассчитывают по уравнению расхода для
газового потока:
V
(6.35)
D
0.785ω
где V – расход газа, проходящего через абсорбер, м3/с; ω – скорость газа, отнесенная к
полному поперечному сечению колонны (фиктивная), м/с.
Скорость газа ω находят следующим путем.
Сначала рассчитывают фиктивную скорость газа ω3 в точке захлебывания (инверсии)
по уравнению (при ρж >> ρг):
0.125
 ω 2з σρ г μ 0.16

 L   ρг 
ж

lg 

А

1.75
(6.36)
   
3

gV
ρ
 G   ρж 
св ж


Здесь σ – удельная поверхность насадки, м2/м3; g – ускорение свободного падения,
м/с2; Vсв – свободный объем насадки, м3/м3; ρг и ρж – плотности газа и жидкости, кг/м3;
μж – динамический коэффициент вязкости жидкости, мПа·с; L и G – массовые расходы
жидкости и газа, кг/с; А = 0,022 для насадки из колец или спиралей.
Затем определяют рабочую скорость газа ω (фиктивную), принимая для абсорберов,
работающих в пленочном режиме
ω  0.75  0.9ω з
(6.37)
0.25
Фиктивная скорость газа в насадочных колоннах, работающих при так называемом
оптимальном гидродинамическом режиме (режиме начала подвисания), может быть
определена из уравнения:
Re г  0.045Ar
0.57
G
 
L
0.43
(6.38)
где
Re г 
ωd э ρ г 4ω г

Vсв μ г
σμ г
(6.38 а)
281
ω/Vсв – скорость газа в свободном сечении насадки, м/с,
d 3ρ ρ g
Ar  э г 2 ж (6.38 б)
μг
μг – динамический коэффициент вязкости газа, Па·с.
14. Определение высоты насадочного абсорбера.
а) Через высоту единицы переноса (ВЕП).
Поверхность контакта фаз в абсорбере при пленочном режиме работы:
F  H нSσ
(6.39)
где Hн – высота слоя насадки, м; S = πD2/4 – площадь поперечного сечения колонны,
м2, D – диаметр колонны, м; σ – удельная поверхность сухой насадки, м2/м3, ψ –
коэффициент смоченности насадки, безразмерный.
Высота слоя насадки:
где G – постоянный по высоте колонны расход инертного газа, кг/с или кмоль/с; Кy –
средний
коэффициент




кг
кмоль
 или кмоль/  м 2  с
;
массопередачи, кг/  м 2  с
кг инертного газа 
кг инертного газа 


Y
h 0y 
н
dY
G
– высота единицы переноса, м; n 0y  
– общее число единиц

K y S
Yв Y  Y
переноса.
Из уравнения (6.34) следует:
n 0y 
Yн  Yв
ΔYср
(6.41)
При прямолинейной равновесной зависимости среднюю движущую силу ΔYср
рассчитывают по уравнению (6.32) или (6.33), при криволинейной равновесной
зависимости число единиц переноса пои находят графическим построением или
методом графического интегрирования – см. пример 6.10.
Объемным коэффициентом массопередачи Ky v называют величину
K yV  K y  K y a
(6.42)
где а = σψ – удельная смоченная (активная) поверхность насадки, м2/м3; при ψ = 1 а = σ.
282
Применяя объемный коэффициент массопередачи, получаем для высоты единицы
переноса:
G
G
(6.43)
h 0y 

K y S K yVS
б)
Через
высоту,
эквивалентную
теоретической тарелке (ВЭТТ).
Высота слоя насадки Hн может быть
рассчитана также по уравнению:
(6.44)
Hн  h эn т
где hэ – высота, эквивалентная теоретической
тарелке (ВЭТТ) или теоретической ступени
(ВЭТС), м (определяется по экспериментальным
данным); nт – число теоретических тарелок
(ступеней изменения концентрации).
Число теоретических тарелок – ступеней
изменения
концентрации
в
абсорбере Рис. 6.4. Графическое
определяют обычно графическим путем (рис. 6.4). определение
числа
На этом рисунке АВ – рабочая линия, построенная ступеней изменения
по уравнению (6.27) или (6.28), ОС – равновесная концентрации
(теоретических
линия.
15. Критериальные формулы для расчета тарелок) в абсорбере.
коэффициентов массоотдачи в насадочных
абсорберах с неупорядоченной насадкой (навалом) при пленочном режиме.
а) Для газовой фазы:
Prг 0.33
Nu г  0.407Re 0.655
(6.45)
г
β d
Nu г  г э
Dг
Re г 
4ω г
 уравнение 6.38 а 
σμ г
μ

Prг  г
ρг Dг
кмоль
м
 ; Dг– коэффициент
кмоль с
м2  с
м3
диффузии поглощаемого компонента в газе, м2/с, Остальные обозначения – см.
формулы (6.36) и (6.39).
Уравнение (6.45) справедливо при значениях Reг от 10 до 10000.
где βг – коэффициент массоотдачи для газа,
283
б) Для жидкой фазы:

Nu ж  0.0021Re 0.75
ж Prж 
0.5
(6.46)
где
Nu ж 
β ж δ пр
Dж
;
Re ж 
4L
;
Sσμ ж
Prж 
μж
ρж Dж
1
 μ 2ж  3
βж – коэффициент массоотдачи для жидкости, м/с; δ пр   2  – так называемая
 ρжg 
приведенная толщина жидкой пленки, м; Dж – коэффициент диффузии поглощаемого
компонента в жидкости, м2/с; L – массовый расход жидкости, кг/с.
Выражение для критерия Reж получено следующим путем.
Обозначения – см. уравнения (6.36) и (6.39).
Омываемый жидкостью периметр сечения абсорбера находим из уравнения (6.39):
(6.47)
П  F/H н  S
Скорость течения пленки жидкости через насадку:
ω ж.пл 
L
L

ρ ж Пδ ρ ж S
где δ – средняя толщина пленки, м.
Эквивалентный диаметр жидкой пленки:
d пл  4П/П  4δ
(6.48)
(6.49)
Подставляя эти значения в выражение для критерия Reж, получаем:
ω d ρ
4L
(6.50)
Re ж  ж.пл пл ж 
μж
Sμ ж
16. Определение диаметра и высоты тарельчатой абсорбционной колонны
проводится так же, как и для тарельчатых ректификационных колонн – см. гл. 7.
Диаметр тарельчатого абсорбера рассчитывают по уравнениям (7.16) и (7.17). Высоту
тарельчатой части абсорбера Нт определяют по уравнению (7.18). Требуемое число
тарелок находят графически с применением кинетических зависимостей для расчета
коэффициентов массопередачи или ВЕП. При приближенных расчетах для
определения числа тарелок находят графически число ступеней изменения
концентрации (рис. 6.4) и затем число тарелок η по уравнению (7.19).
ПРИМЕРЫ
Пример 6.1. Жидкая смесь содержит 58,8% (мол.) толуола и 41,2% (мол.)
четыреххлористого углерода (ч. х. у). Определить относительную массовую
 кг толуола 
 и его объемную массовую концентрацию С х
концентрацию толуола Х  в
 кг ч.х.у 
(в кг/м3).
284
Решение. Относительная массовая концентрация толуола:
Х
М тол x
М ч.х.у 1  x 
где Мтол – мольная масса толуола (92 кг/кмоль); Мч.х.у – то же четыреххлористого
углерода (154 кг/кмоль); х – мольная доля толуола. Имеем:
92  0.588
кг толуола
Х
 0.853
154  0.412
кг ч.х.у
Чтобы рассчитать объемную массовую концентрацию толуола С х , необходимо
знать плотность смеси ρсм. Для расчета плотности предварительно найдем массовую
долю толуола х .
Х
0.853
х

 0.461
1  Х 1.853
Плотность толуола ρтол = 870 кг/м3, плотность четыреххлористого углерода ρч.х.у =
=1630 кг/м3.
Считая, что изменение объема при смешении не происходит, т. е. объем смеси
равен сумме объемов компонентов, находим объем 1 кг смеси
0.461 0.539

 0.862  10 3 м 3
870
1630
откуда плотность смеси
1
ρ см 
 1160 кг/м3
0.862  10 3
Можно рассчитать ρсм и так:
1 Х
1  0.853

 1160 кг/м 3
1
0.853
1
Х


ρ ч.х.у ρ тол 1630 870
Объемная массовая концентрация толуола:
Сх  ρх  1160  0.461 =535 кг/м3
ρ см 
Пример 6.2. Воздух атмосферного давления при температуре 34°С насыщен
водяным паром. Определить парциальное давление воздуха, объемный и массовый %
пара в воздушно-паровой смеси и его относительную массовую концентрацию, считая
оба компонента смеси идеальными газами. Атмосферное давление 745 мм рт. ст.
Определить также плотность воздушно-паровой смеси, сравнить ее с плотностью
сухого воздуха.
Решение. При t = 34°С давление насыщенного водяного пара составляет 39,9 мм рт.
ст. Эго давление является парциальным давлением водяного пара ρп в
285
воздушно-паровой смеси, а парциальное давление воздуха равняется:
ρ в  П  ρ п  745  39.6  705 мм рт. ст.
Мольная (объемная) доля водяного пара в смеси:
у = ρп/П = 39,9/745 = 0,0535
Массовая доля пара:
Mп y
18  0.05335
y

 0.0339
M п y  M в 1  y 18  0.0535  29  0.9465
Относительная массовая концентрация:
Y
y
0.0339
кг пара

 0.0351
1  y 0.9661
кг воздуха
Плотность воздушно-паровой смеси рассчитываем как
компонентов, взятых каждая при своем парциальном давлении:
ρсм  ρв  ρп 

сумму
плотностей
М в ρв Т 0 М п ρ п Т 0
Т0
М в ρв  М п ρп  


22.4ТП 0 22.4ТП 0 22.4ТП 0
273
29  705  18  39.9  1.105 кг/м 3
22.4  307  760
Можно рассчитать плотность смеси иначе.
Мольная масса смеси:
М см  М п y  М в 1  y  18  0.0535  29  0.9465 28,4 кг/кмоль
Плотность смеси при Π = 745 мм рт. ст. и t = 34°С:
М ПТ
28.4  745  273
ρ см  см 0 
 1.105 кг/м 3
22.4ТП 0 22.4  307  760
Плотность сухого воздуха при тех же давлении и температуре:
ρ с.в 
М в ПТ 0
29  745  273

 1.13 кг/м 3
22.4ТП 0 22.4  307  760
Пример 6.3. При температуре 25°С приведены в соприкосновение: воздух
атмосферного давления, содержащий 14% (об.) ацетилена (С2Н2), и вода, содержащая
растворенный ацетилен в количестве: а) 0,29·10-3 кг на 1 кг воды; б) 0,153·10-3 кг на 1 кг
воды. Определить: 1) из какой фазы в какую будет переходить ацетилен; 2) движущую
силу этого процесса перехода в начальный момент времени (в относительных мольных
концентрациях). Атмосферное давление 765 мм рт. ст. Равновесные концентрации
ацетилена в газовой и в жидкой фазах определяются законом Генри.
Решение. Закон Генри [уравнение (6.2)]:
р* = Ех
При t = 25°С коэффициент Генри Ε = 1,01·106 мм рт. ст.
286
Парциальное давление ацетилена в воздухе по уравнению (6.1):
ρ = yΠ = 0,14 · 765= 107 мм рт. ст.
а) Мольная доля ацетилена в воде при Х = 0,29·10-3 кг ацетилена/ кг воды (табл.
6.2):
х
Х
0.29  10 3
18  0.29  10 3


 0.2  10 3
М ац
26
26
0.29  10 3 
Х
18
Мв
Ответы на вопросы примера могут быть получены двумя путями.
I. В условиях равновесия парциальное давление ацетилена в газовой фазе над
жидкостью с х = 0,2·10 -3 по закону Генри должно составлять:
р* = Еx = 1,01 · 106 · 0.2 ·10-3 = 202 мм рт. ст.
Имеющееся в действительности над этой жидкостью парциальное давление
ацетилена меньше: ρ = 107 мм pт. ст. Чтобы в процессе массопередачи система газ –
жидкость приближалась к состоянию равновесия, парциальное давление ацетилена в
газовой фазе должно увеличиваться, т. е. он будет переходить из воды в воздух.
Движущая сила этого процесса перехода (отклонение от состояния равновесия) в
начальный момент времени будет равна: в единицах парциального давления
ацетилена
∆р = р* – ρ = 202 – 107 = 95 мм рт. ст.
в мольных долях
Δy  y   y 
202
 0.14  0.264  0.14  0.124
765
в относительных мольных концентрациях
ΔY  Y   Y 
y
y
0.264
0.14
кмоль ацетилена



 0.196

кмоль воздуха
1  y 1  y 1  0.264 1  0.14
II. В условиях равновесия с газовой фазой, в которой парциальное давление
ацетилена равняется 107 мм рт. ст., вода по закону Генри должна иметь
концентрацию ацетилена (в мольных долях):
х 
p
107

 0.106  10 3
6
E 1.01  10
Имеющаяся в действительности мольная доля ацетилена в воде больше: х =
0,2·10-3. Для того чтобы в процессе массоперехода система приближалась к
состоянию равновесия, мольная
287
доля ацетилена в воде должна уменьшаться, т. е. ацетилен будет переходить из
воды в воздух.
Движущая сила этого процесса перехода в начальный момент времени (считая
ее по концентрации в жидкой фазе):
в мольных долях
х  х  х   0.2  10 3  0.106  10 3  0.094  10 3
в относительных мольных концентрациях
Х  Х  Х  
х
х

1  х 1  х
Так как в данном примере х и х* оба много меньше единицы, то в
знаменателях последнего уравнения ими можно пренебречь и
Х  х  х   0.094  10 3
кмоль ацетилена
кмоль воды
б) Мольная доля ацетилена в воде:
х
18  0.153  10 3
 0.106  10 3
26
Перехода ацетилена из одной фазы в другую не будет, так как соприкасающиеся
фазы находятся в равновесии:
х  х   0.106  10 3 ;
y  y   0.14
Пример 6.4. В массообменном аппарате, работающем под давлением рабс =
3,1кгс/см2,
коэффициенты
массоотдачи
имеют
следующие
кмоль
кмоль
,  x  22 2
значения:  y  1.07 2
. Равновесные составы газовой и
м  чy  1
м  чx  1
жидкой фаз характеризуются законом Генри p  = 0,08·106х;. Определить: а)
коэффициенты массопередачи К.у и Кх, б) во сколько раз диффузионное сопротивление
жидкой фазы отличается от диффузионного сопротивления газовой фазы.
Решение. Приведем уравнение равновесия к виду у* = mх:
p  0.08  10 6
y 

x  35.1x
П
3.1  735
Находим коэффициенты массопередачи:
1
1
1
кмоль
Кy 


 0.396 2
1
m
1
35.1 0.935  1.595
м  чy  1


 y  x 1.07 22
1
1
1
кмоль


 13.9 2
1
1
1
1
0.0266  0.0455
м  чx  1


m y  x
35.1  1.07 22
Проверка:
К х/К y = 13,9/0,396 = 35,1 = m
Отношение диффузионных сопротивлений жидкой и газовой
фаз при движущей силе Δy:
m 1 1.595
:

 1.71
 x  y 0.935
Такое же отношение будет и при движущей силе Δx.
Диффузионное сопротивление жидкой фазы в 1.71 раза больше сопротивления газовой
фазы.
Пример 6.5. В массообменном аппарате – абсорбере коэффициент
кмоль
массопередачи. K y  10.4
Инертный газ (не переходящий в жидкость) –
кмоль
2
м ч
м3
азот. Давление рабс в аппарате 760 мм рт. ст., температура 20 °С. Определить значения
кмоль
коэффициента массопередачи Kу в следующих единицах: 1) 2
;
м  ч Δy  1
кмоль
кг
2) 2
; 3)
.
кг
м  ч  мм рт.ст
2
м ч
кг инертного газа
Решение. Напишем равенства:
M  K y ΔC y F  K y ΔyF  K y ΔpF
Kx 
где М – мольный расход переходящего в жидкость компонента, кмоль/ч.
Отсюда: 1)
K y ΔC y  K y Δy
K y  K y
ΔC y
Δy
ПТ 0
ρ
y
y
M см
22.4П 0 Т
В данном примере Π = П0 и
ΔС y
T0
273


 0.0416
Δy
22.4T 22.4  293
ΔC y
кмоль
K y  K y
 10.4  0.0416  0.433 2
Δy
м  ч Δy  1
2) K y Δy  K y Δp
По уравнению (6.1):
p
Δp
y ;
Δy 
П
П
Δy K y 0.433
кмоль
K y  K y


 5.69  10  4 2
Δp
П
760
м  ч  мм рт.ст
Cy 
или
5.69  10  4
кмоль
 1.19  10 9 2
3600  133.3
м  с  Па
289
3) Из равенств
W  M к M  М к Кy ΔyF  KyΔyF  KyΔYF
(где W — массовый расход переходящего компонента, кг/ч) находим:
Δy
К y  K y M к
ΔY
Mк y
Y
M и.г (1  y)
Здесь Mк и Ми.г – мольные массы переходящего компонента и инертного газа. При
малых значениях у:
M
Y к y
M и.г
Отсюда
Δy M и.г

ΔY М к
К y  K y
M к Δy
 K y M и.г  0.433  28  12.1
ΔY
кг
кг
кг инертного газа
Пример 6.6. Вычислить коэффициент диффузии сероводорода в воде при 40 °С.
Решение. Сначала вычислим коэффициент диффузии при 20 °С по формуле (6.22):
м2  ч
D 20 
1  10 6
2
1
1

MA MB
AB μ  υ A3  υ B3 


Для сероводорода
А=1
ол = 2·3,7+25,6 = 33,0 (табл. 6.3)
МА = 34
1
1
Для воды
В = 4,7
μ = 1 сП = I мПа·с
υВ=2·3,7 + 7,4 =
МВ = 18
Подставляем эти значения в формулу (6.22):
2
1  10 6
1
1
9 м
D 20 


1.93

10
2
1
1
18 34
с
4.7  114.8 3  33 3 


Вычисляем температурный коэффициент b по формуле (6.24):
0.2 μ
0.2 1
b
3
 0.02
3 ρ
1000
Искомый коэффициент диффузии по формуле (6.23) равняется:
D40 = 1,93 · 10-9 [1 + 0,02 (40 – 20)] = 2,7 · 10-9 м2/с
290
Для сравнения рассчитаем коэффициент диффузии сероводорода в воде при 40 °С по
формуле (6.25):
0.5
7.4  10 12 2.6  18  313 7.4  10 12  6.83  313
D 40 

 2.96  10 9 м 2 с
0.6
0.656  8.15
0.656  33
Здесь 0,656 сП – динамический коэффициент вязкости воды при 40 °С .
Пример 6.7. Определить расход серной кислоты для осушки воздуха при
следующих данных. Производительность скруббера 500 м3/ч (считая на сухой воздух
при нормальных условиях). Начальное содержание влаги в воздухе 0,016 кг/кг сухого
воздуха, конечное содержание 0,006 кг/кг сухого воздуха. Начальное содержание воды
в кислоте 0,6 кг/кг моногидрата, конечное содержание 1,4 кг/кг моногидрата. Осушка
воздуха производится при атмосферном давлении.
Решение. Массовый расход воздуха:
G=500 · 1,293 = 646 кг/ч
где 1,293 кг/м3 – плотность воздуха при нормальных условиях. По уравнению (6.26)
расход серной кислоты (моногидрата)
Y  Yв
0.016  0.006
LG н
 646
 8.1 кг ч
Xн  Xв
1.4  0.6
Пример 6.8. Скруббер для поглощения паров ацетона из воздуха орошается водой в
количестве 3000 кг/ч. Средняя температура в скруббере 20°С. Через скруббер
пропускается под атмосферным давлением смесь воздуха с парами ацетона,
содержащая 6% (об.) ацетона. Чистого воздуха в этой смеси содержится 1400 м3/ч
(считая на нормальные условия). В скруббере улавливается 98% ацетона.
Уравнение линии равновесия;
Y*=1.68X
где X и Υ* выражены в киломолях ацетона на 1 кмоль второго компонента, т. е. воды
или воздуха.
Найти диаметр и высоту скруббера, заполненного керамическими кольцами
размером 25 × 25 × 3 мм. Скорость газа принять на 25% меньше скорости
захлебывания.
Коэффициент массопередачи Кy = 0,4 кмоль ацетона/(м2 · ч×
кмоль ацетона
).
кмоль воздуха
Коэффициент смоченности насадки принять равным единице.
Решение. Количество поглощаемого ацетона:
Vи.г y н с п
1400  0.06  0.98
M

 3.9 кмоль ч
1  y н  22.4
0.94  22.4
где сп = 0,98 – степень поглощения,
291
Начальная концентрация ацетона в воде, подаваемой на верх скруббера, Хв = 0.
Конечная концентрация ацетона в воде, вытекающей внизу из скруббера:
M
3.9
кмоль ацетона
Xн 

 0.0234
L M в 3000 18
кмоль воды
Начальная концентрация ацетона в воздухе внизу при входе в
скруббер:
yн
0.06
Yн 


1  y н 0.94
кмоль ацетона
кмоль воздух
Конечная концентрация ацетона в воздухе, выходящем из скруббера:
y 1  с П  0.06  0.02
Yв  н


1  yн
0.94
 0.0639
 0.00128
кмоль ацетона
кмоль воздуха
По этим точкам на диаграмме Y-X (рис. 6.5) нанесена
Рис. 6.5
рабочая линия по уравнению Y* = 1.68X
Находим движущую силу абсорбции в низу скруббера:
кмоль ацетона
ΔY   Yн  Yн  0.0639  0.0393  0.0246
кмоль воздуха

Значение Yн находим по уравнению равновесной линии для Yн соответствующего
низу скруббера:
кмоль ацетона
Yн  1.68X н  0.0639  0.0393  0.0246
кмоль воздуха
Движущая сила абсорбции на верху скруббера:
кмоль ацетона
ΔYв  Yв  Yв  0.00128  0  0.00128
кмоль воздуха
Средняя движущая сила:
ΔYн  ΔYв 0.0246  0.00128
кмоль ацетона
ΔYср 

 0.0079
ΔYн
0.0246
кмоль воздуха
2.3lg
2.3lg
0.00128
ΔYв
292
Требуемую поверхность массопередачи находим по уравнению:
M
3.9
F

 1230 м 2
K y ΔYср 0.4  0.0079
Объём слоя керамических колец, необходимый для создания найденной поверхности,
при ψ=1:
V  H н S  F/σ  1230/204  6 м 3
где σ = 204 м2/м3 – удельная поверхность насадки.
Определим сечение скруббера.
По уравнению (6.36) вычисляем фиктивную скорость газа в точке инверсии,
пренебрегая небольшим содержанием ацетона в жидкости и газе.
Значения входящих в уравнения величин:
T
273
L  3000 кг/ч; ρ г  ρ 0 0  1.293
 1.2 кг/м 3
T
293
G  1400  1.293  1810 кг/ч; ρ ж  1000 кг/м 3
L/G  3000/1810  1.66; ρ г /ρ ж  1.2/1000  0.0012
μ ж  1ммП с; Vсв  0.74 м 3 /м 3
Подставляем эти значения в формулу (6.36):
 ω 2  204  0.0012 0.16 
lg  з
1   0.022  1.75  1.66 0.25  0.0012 0.125
3
 9.81  0.74

или
lg 0.0616 ω 2з  0.825
откуда ωз = 1.56 м/с.
По условию берём рабочую фиктивную скорость газа ω на 25 % меньше:
ω  0.75 ω з  0.75  1.56  1.17 м/с
Площадь поперечного сечения скруббера:
G
1810
S

 0.35 8 м 2
3600 ω ρ г 3600  1.17  1.2
Отсюда диаметр скруббера
0.358
D
 0.675 м
0.785
Требуемая высота насадки:
H н  V/S  6/0.358  16.8 м
Пример 6.9. Определить коэффициент массопередачи в водяном скруббере при
поглощении из газа двуокиси углерода по следующим данным.В скруббер поступает
5000 м3/ч газовой смеси, считая при атмосферном давлении и при рабочей температуре.
На скруббер подаётся 650 м3/ч чистой воды. Начальное содержание двуокиси углерода
в газе 28.4 %(об.), конечное (в вверху скруббера) 0.2 % (об.). Давление в скруббере
pабс.=16.5 кгс/см2.Температура 15°С. В нижнюю часть скруббера загружено 3 тонны
керамических колец 50×50×5 мм. Выше загружено 17 тонн колец 35×35×4 мм.
Коэффициент смоченности считать равным единице.
Решение. Вычислим суммарную поверхность всех колец. Поверхность колец
50 × 50 × 5 мм:
G
3000
f 1  1 σ1 
87.5  495 м 2
ρ1
530
где ρ1 = 530 кг/м3 – насыпная плотность насадки из колец 50×50×5 мм; σ1 = 87,5 м2/м3 –
удельная поверхность насадки .
Аналогично вычисляем поверхность колец 35×35×4 мм:
G2
17000
σ2 
140  4717 м 2
ρ2
505
Суммарная поверхность всех колец:
F =f 1+f2 =495+4717 = 5212 м2
Определим количество двуокиси углерода, поглощенной водой.
Начальное количество двуокиси углерода в газе (в низу скруббера) :
VнCO2  VнСМ y н  5000  0.284  1420 м 3 /ч
f2 
Количество двуокиси углерода в выходящем газе (в верху скруббера) :
VнСМ  VнСО2
5000  1420
VвСО2  VвСМ y в 
yв 
0.002  7.2 м 3 /ч
1  yв
1  0.002
Поглощается водой:
Vпогл  VнСО2  VвСО2  1420  7.2  1412.8 м 3 /ч p  1 кгс/см 2 , или 0.1М.1 , и t  15  C

или
Vпогл Т 0
1412.8  273
ρ0 
1.976  2630 кг/ч , т т. 2630/44  60 кмоль/ч
Т
273  15
Здесь 1,976 кг/м3 – тность СО2 при нормальных условиях; 44 кг/кмоль –мольная масса
СО2.
Находим движущую силу процесса абсорбции в низу скруббера.
Парциальное давление двуокиси углерода на входе в скруббер:
рн = Пyн = 0,284 · 1620 = 460 кПа
где 1620 = 16,5·98,1 кПа –общее давление в скруббере.
Мольная доля СО2 в воде, вытекающей из скруббера:
G CO 2 /M CO 2
2630/44
xн 

 0.00166
G CO 2 G H 2O
2630 650000


44
18
M CO
MH O
G погл 
2
2
Коэффициент Генри Е для двуокиси углерода при 15 °С равен 0,93·106 мм рт. ст.,
или 0,124·106 кПа; отсюда парциальное давление двуокиси углерода в газе,
равновесном с жидкостью, вытекающей из скруббера [уравнение (6.2)]:
p н  Ех н  0.00166  0.124  10 6 = 206 кПа
Движущая сила процесса абсорбции в низу скруббера:
Δp н  p н  p н = 460 — 206 = 254 кПа
Определяем движущую силу процесса абсорбции на верху скруббера.
Парциальное давление двуокиси углерода в газе, выходящем вверху из скруббера:
рв = Пyв = 1620 · 0,002 = 3,24 кПа
Так как вода на орошение скруббера подается чистая, то парциальное давление
двуокиси углерода в равновесном с водой газе равно нулю; отсюда движущая сила
процесса абсорбции на верху скруббера:
Δp в  p в  p в = 3,24 – 0 = 3,24 кПа
Средняя движущая сила для всего процесса:
254  3.24
Δp ср 
 57.4 кПа
254
2.3lg
3.24
Коэффициент массопередачи.

M
2630
кг

 0.0088 2
Fp ср 5212  57.4
м  ч  кПа
Если коэффициент массопередачи отнести к разности давлений Δp, выраженной в
мм рт. ст., то получим следующее его значение:
2630
кг
К Δp 
 0.0012 2
57.4
м  ч  кПа
5212
0.133
Пример 6.10. В скруббере аммиак поглощается водой из газа под атмосферным
давлением. Начальное содержание аммиака в газе 0,03 кмоль/кмоль инертного газа.
Степень извлечения равна 90%. Вода, выходящая из скруббера, содержит аммиака 0,02
кмоль/кмоль воды. Путем отвода теплоты в скруббере поддерживается постоянная
температура.
Данные о равновесных концентрациях аммиака в жидкости и газе при температуре
поглощения приведены в табл. 6.5.
297
K Δp 
Т а б л и ц а 6.5
X,
кмоль аммиака
кмоль воды
0
0,005
0,010
0,0125
Y*,
X,
Y*,
кмоль аммиак
кмоль инертного газа
кмоль аммиака
кмоль воды
кмоль аммиака
кмоль инертного газа
0
0,0045
0,0102
0,0138
0,015
0,020
0,023
0,0183
0,0273
0,0327
Определить требуемое число единиц переноса n 0y : 1) графическим
построением; 2) методом графического интегрирования.
Решение. 1) По данным табл. 6.5 на рис. 6.6
построена равновесная линия АВ. На этом же
графике нанесена рабочая линияCD. Она
проходит через точку С с координатами ;X в = 0,
Y в = 0,03 ( 1 – 0,9) = 0,003 (верх скруббера) и
точку D с координатами Х н = 0,02, Y н = 0,03
(низ скруббера).
Число
единиц
переноса
n 0y
находим
следующим путем. Отрезки ординат между
рабочей и равновесной линиями разделены
пополам; через середины их проведена
вспомогательная пунктирная линия. Затем
начиная от точки С, построение выполнено
таким образом, что для каждой ступени ab = bc.
Каждая из полученных ступеней представляет
собой единицу переноса, т. е. каждой ступени
соответствует такой участок аппарата, на
котором изменение рабочей концентрации(Y 1 – Y 2 )·равно средней движущей
силе на этом участке (Y – Y*) ср.
Всего получено 5,82 ступени (последняя неполная ступень равна
отношению отрезков Dd/ef = 0,82):
n 0y = 5,82
Как следует из графика, на нижнем участке кривой равновесия, где ее
наклон меньше наклона рабочей линии, единица переноса меньше ступени
изменения концентрации; на верхнем
298
участке равновесной линии, где ее наклон больше наклона рабочей линии, наблюдается
обратная картина.
2) Для определения числа единиц переноса методом графического интегрирования
по данным табл. 6.5 и рис. 6.6 составляем табл. 6.6.
Таблица 6.6
X
Y
Y*
0
0,005
0,010
0,0125
0,015
0,020
0,003
0,0097
0,0165
0,0200
0,0234
0,0300
0
0,0045
0,0102
0,0138
0,0183
0,0273
Y — Y*
0,003
0,0052
0,0063
0,0062
0,0051
0,0027
1
Y  Y
333
193
159
161
196
371
По данным последней таблицы строим график 1/(Y – Y*) = f(Υ)–рис. 6.7.
Подсчитываем па этом графике отмеченную
штриховкой площадь (например, методом трапеций)
(см. пример 4.21). Величина этой площади (5,83) дает
YH  0.03
dY
значение интеграла
, т.е.число единиц


Y

Y
YB  0.003
переноса n0y.
Пример
6.11.
Определить
теоретически
минимальный расход жидкого поглотителя с мольной
массой 224 кг/кмоль, необходимый для полного
извлечения пропана и бутана из 1000 м3/ч (считая при
нормальных условиях) газовой смеси. Содержание
пропана в газе 15% (об.), бутана 10% (об.).
Температура в абсорбере 30°С, абсолютное давление
3 кгс/см2 (294 кПа). Растворимости бутана и пропана
в поглотителе характеризуются законом Рауля.
Решение Максимальная концентрация (мольная Рис. 6.7. Определение числа единиц
переноса методом графического
доля) пропана в поглотителе, вытекающем из интегрирования (к примеру 6.10).
скруббера
(равновесная
с
входящим
газом),
определяется по уравнению (6.8):
П
294
x П 
yП 
0.15  0.045
PП
981
299
где Рп = 981 кПа (10 кгс/см2) – давление насыщенного пара пропана при 30 °С.
Количество содержащегося в газовой смеси пропана, которое требуется поглощать:
Vy П 1000  0.15
GП 

 6.7 кмоль ч
22.4
22.4
Минимальный расход поглотителя для поглощения пропана определяется из
уравнения:
L мин x П
 GП
1  х П
откуда


G 1  x П
6.7  0.955

 142 кмоль ч

0.045
xП
или 142·224 = 31 800 кг/ч.
Наибольшая возможная концентрация бутана в поглотителе, вытекающем внизу из
скруббера:
П
294
x б 
yб 
0.1  0.11
Рб
265
где Рб = 265 кПа (2,7 кгс/см2) – давление насыщенного пара бутана при 30 °С.
Количество поглощаемого бутана:
Vy б 1000  0.1
Gб 

 4.47 кмоль ч
22.4
22.4
Минимальный расход поглотителя для поглощения бутана:
G (1  x б ) 4.47  0.89
L мин  б

 36.1 кмоль ч
xб
0.11
Минимальный расход поглотителя для полного поглощения бутана значительно
меньше, чем для поглощения пропана, следовательно, найденным выше количеством
поглотителя (142 кмоль/ч) бутан будет полностью уловлен.
Пример 6.12. Определить коэффициент массоотдачи для газовой фазы в насадочном
абсорбере, в котором производится поглощение двуокиси серы из инертного газа
(азота) под атмосферным давлением. Температура в абсорбере 20 °С, он работает в
пленочном режиме. Скорость газа в абсорбере (фиктивная) 0,35 м/с. Абсорбер заполнен
кусками кокса (σ = 42 м2/м3, Vсв = 0,58 м3/м3).
Решение. По уравнению (6.45):
Prг 0.33
Nu г  0.407Re 0.655
г
L мин 
где
4ωωг
4  0.35  1.16

 2210
σμ г
42  0.0175  10 3
28  273
ρг 
 1.16 кг м 3 ; μ г  0.175  10 3 Па  с
22.4  293
300
Коэффициент диффузии Dr принимаем такой же, как в воздухе. Имеем:
Re г 
1.5
 293 
6
2
D г  10.3  10 6 
  11.45  10 м с
 273 
μ
0.0175  10 3
Prг  г 
 1.32
ρ г D г 1.16  11.45  10 6
Диффузионный критерий Нуссельта:
βd
Nu г  г э  0.407  2210 0.655  1.32 0.33  69
Dг
Эквивалентный диаметр
4Vсв 4  0.58
dэ 

 0.055 м
σ
42
Коэффициент массоотдачи:
Nu г D г 69  11.45  10 6
βг 

 144  10 4 м с
dэ
0.055
Пример 6.13. Из критериального уравнения (6.45) вывести расчетную формулу для
определения высоты единицы переноса по газовой фазе.
Решение. Из уравнения (6.12)
1
1 m


Ку βу βx
в котором Ку, βу и βx выражены в кмоль/(м2·с), получаем
G
G
mG L


K y Sσ β y Sσ
L β x Sσ
или в соответствии с уравнением (6.43) при ψ = 1
mG
h 0y  h y 
hx
L
где G и L – мольные расходы газа и жидкости, кмоль/с; S – поперечное сечение
абсорбера, м2; σ – удельная поверхность насадки, м2/м3; hy = G/(βySσ) – высота единицы
переноса для газовой фазы, м; hx = L/(βxSσ) – то же для жидкой фазы, м.
В критериальном уравнении (6.45)
Prг 0.33
Nu г  0.407Re 0.655
г
где Nu г 
βгdэ
коэффициент массоотдачи βг выражен в
Dг
кмоль
 м/с
кмоль
2
м с
м3
Соотношение между βy и βг находим из уравнения:
β y Δy  β г ΔС y
301
откуда
β y  βг
ΔС y
Δy
 βг
ρг
М см
(см. табл. 6.2)
Тогда
hy 
GM см
G
ω


β y Sσ β г ρ г Sσ β г σ
и
βг 
ω
h yσ
GM см
фиктивная скорость газа, м/с.
ρгS
Подставляя найденное значение βг в выражение для диффузионного критерия
Нуссельта, получаем
ωd э μ г ρ г
ωρ г μ г d э Re г Prгd э
Nu г 


h y σD г μ г ρ г σμ г D г ρ г h y
4h y
и из уравнения (6.45)
где ω 
 
h y  0.615d э Re 0.345
Prг
г
Пример 6.14. В скруббере с насадкой из керамических колец 50×50×5 мм (навалом)
производится поглощение двуокиси углерода водой из газа под давлением рабс = 16
кгс/см2 (1,57 МПа) при температуре 22 °С Средняя мольная масса газа 20,3 кг/кмоль,
динамический коэффициент вязкости газа при рабочих условиях 1,31·10-5 Па·с,
коэффициент диффузии СО2 в инертной части газа 1,7·10-6м2/с. Средняя фиктивная
0.67
скорость газа в скруббере 0,041 м/с, плотность орошения (фиктивная скорость
жидкости) 0,064 м3/(м2·с). Определить общую высоту единицы переноса h0y, принимая
коэффициент смоченности насадки ψ равным единице.
Решение. Общая высота единицы переноса (см. предыдущий пример) :
mG
h 0y  h y 
hx
L
Находим hy – высоту единицы переноса для газовой фазы
Prг 0.67
h y  0.615d э Re 0.345
г
Характеристики насадки Vсв = 0,785 м3/м3 и σ = 87,5 м2/м3. Таким образом
4Vсв 4  0.785
dэ 

 0.0359м
σ
87.5
4ωωг
4  0.041  13.4
Re г 

 1920
σμ г
87.5  1.31  10 5
302
Здесь
М г ПТ 0
20.3  16  273
ρг 

 13.4 кг м 3
22.4П 0 Т
22.4  295
μг
1.31  10 5

 0.575
ρ г D г 13.4  1.7  10 6
Высота единицы переноса для газовой фазы:
h y  0.615  0.0359  19200.345  0.5750.67  0.205 м
Находим hx – высоту единицы переноса для жидкой фазы по формуле
 0.5
h x  119δ пр Re 0.25
ж Prж 
Prг 
полученной из уравнения (6.46) так же, как в предыдущем примере из уравнения
(6.45) получено выражение для h y.
Значения физико-химических констант для воды при 22 °С: ρ ж = 1000 кг/м3; μж =
0,958·10-3 Па·с; Dж = 1,87·10-9м2/с .
Приведенная толщина жидкой пленки:
1
 μ 2ж  3  0958 2  10 6 
  4.55  10 5 м
δ пр   2   
6
 10  9.81 
 ρжg 
По условию плотность орошения:
Lm
 0.064 м 3 / м 2  с
Sρ ж
Здесь Lm – массовый расход жидкости, кг/с.
Массовая плотность орошения:
Lm/S = 0,064ρж = 64 кг/(м2 · с)
По уравнению (6.50):
4L m
4  64
Re ж 

 3060
Sσσψ ж 87.5  0.958  10 3


μж
0.958  10 3

 512
ρ ж D ж 1000  1.87  10 9
Высота единицы переноса для жидкой фазы:
hx = 119 · 4,55· 10-5·3060 0.25·5120.5 = 0,91 м
Находим отношение мольных расходов газа и жидкости G/L. Из уравнения расхода
Prж 
для газа ω  GM г /ρ г S получаем:
G/S = ωρг/Мг = 0,041 · 13,4/20,3 = 0,0271 кмоль/(м 2 · с)
Для жидкости:
L
L
64
 m 
 3.56 кмоль/(м 2  с)
S SM ж 18
303
Отсюда
G/L = 0,0271/3,56 = 0,00761
Коэффициент распределения m в уравнении (6.12):
E 1.144  10 6
= 97,3 – см. уравнение(6.3)
m 
П
16  735
где коэффициент Генри Е = 1,144·106 мм рт. ст. (при 22°С). Общая высота единицы
переноса:
mG
h 0y  h y 
h x = 0,205 + 97,3 · 0,00761 · 0,91 = 0,205 + 0,675 = 0,88 м
L
Пример 8.15. По данным примера 6.8 определить число единиц переноса в абсорбере с
учетом обратного (продольного) перемешивания.
Решение. Число единиц переноса для условий идеального вытеснения, т. е. без учета
обратного перемешивания, составляет:
Y  Yв 0.0639  0.00128
n 0y  н

 7.93
ΔYср
0.0079
Искомое число единиц переноса с учетом обратного перемешивания n 0y находим из
уравнения
1
1
1


n 0y n 0y n обр
в котором поправка на обратное перемешивание n обр равняется:
n обр 
АlnA
Φ  Peпр
A 1
где
L
0.05  А 
А
;Φ  1
mG
Peпр 0.25  n 0y 
0.5
Значение критерия Ре´пр вычисляют по уравнению;
1
1
1


Peпр Аf г Peм.г f ж Рем.ж
где
fг 
n 0y  6.8A 0.5
n 0y  6.8A
1.5
; fж 
n 0y  6.8A 0.5
n 0y  6.8A
 0.5
; Peм.г 
ωг H
ω H
; Peм.ж  ж
Eг
Eж
– модифицированные критерии Пекле для газа и жидкости; ωг и ωж – скорости потоков
газа и жидкости, м/с; Ег и Еж – соответствующие коэффициенты обратного
перемешивания, м2/с; Н – рабочая длина аппарата – высота слоя насадки, м.
304
По данным примера 6.8 находим:
L Yн  Yв 0.0639  0.00128


 2.67
G X н  X в
0.0234  0
dY 
L
2.67
 1.63;
А

 1.59
dX
mG  1.68
Примем предварительно n 0y = 9. Тогда
m
9  6.8  1.59 0.5
9  6.8  1.59 0.5

0.78;
f

 1.22
ж
9  1.68  1.591.5
9  6.8  1.59 0.5
Для определения скоростей газа и жидкости (ωг и ωж) необходимо найти доли
поперечного сечения абсорбера, занимаемые каждым потоком в отдельности. Долю
объема насадки δ, занятую жидкостью, рассчитаем по уравнению [6.2]:
σ Г 0.435
δ  4.83  10  4 0.24
dэ
в котором
L
3000
Г c 
 0.0114 кг/ с  м 
Sσ 3600  0.358  204
4Vсв 4  0.74
dэ 

 0.0145 м
σ
204
Подставляя эти значения, находим:
4.83  10 4  204  0.0114 0.435
δ
 0.039
0.0145 0.24
Скорость течения жидкости в слое насадки:
Lc
3000
ωж 

 0.06 м / с
ρ ж S δ 3600  1000  0.358  0.039
Скорость газа:
Gc
1810
ωг 

 1.67 м/с
ρ г SVсв  δ 3600  1.2  0.3580.74  0.039
Величины коэффициентов обратного перемешивания Еж и Ег находят опытным путем.
Для ориентировочного их определения в насадочном абсорбере воспользуемся
критериальными уравнениями.
Для жидкой фазы
ωж d н
 7.58  10 3 Re 0.703
ж
Еж
Для газовой фазы:
ωг d н
 2.4Re г0.2  10 0.002Reж
Ег
305
В этих уравнениях:
d L
d G
Re ж  н c ;
Re г  н c
Sμ ж
Sμ г
где dн – номинальный размер элементов насадки, м.
В нашем случае:
fг 
0.025  3000
 58
3600  0.358  1  10 3
0.025  1810
Re г 
 1930
3600  0.358  0.0182  10 3
Для жидкой фазы:
ωж d н
 7.58  10 3  580.703  130  10 3
Еж
Коэффициент обратного перемешивания в жидкой фазе:
Re ж 
ω ж d н 0.06  0.025

 0.0116 м 2 /с
0.13
0.13
ω Н 0.06  16.8
Peм.ж  ж 
 87
Еж
0.0116
Для газовой фазы:
ωг d н
2.4
2.4
 0.2

 0.403
0.002Reж
0.2
Ег
1930  10 0.00258
Re г  10
Коэффициент обратного перемешивания в газовой фазе:
ωd
1.67  0.025
Ег  г н 
 0.104 м 2 /с
0.403
0.403
ω Н 1.67  16.8
Peм.г  г 
 270
Ег
0.104
Приведенный критерий Пекле:
Еж 

1
1
Peпр  

 Аf г Peм.г f ж Peм.ж
0.05  А 
Φ  1
Репр 0.25  n 0y 
0.5



1
1
1





 1.59  0.78  270 1.22  87 
0.05  1.59 
 1


80.5 0.25  9 
1
 80.5
0.5
 1  0.007  0.993
Поправка на обратное перемешивание:
А  2.3 lgA
1.59  2.3 lg1.59
n обр 
Φ  Peпр 
0.993  80.5  81.7
A 1
0.59
Число единиц переноса с учетом обратного перемешивания:
1
1
 1
1 
1 
 1

n 0y 



  8.8
n

 7.93 81.7 
 0y n обр 
что близко к значению n 0y = 9, принятому в начале расчета.
306
КОНТРОЛЬНЫЕ ЗАДАЧИ
6.1. Смешаны два равных объема бензола и нитробензола. Считая, что объем жидкой
смеси равен сумме объемов компонентов, определить плотность смеси,
относительную массовую концентрацию Х нитробензола и его объемную мольную
концентрацию Сх
6.2. Состав жидкой смеси: хлороформа 20%, ацетона 40%, сероуглерода 40%.
Проценты мольные. Определить плотность смеси, считая, что изменения объема при
смешении не происходит.
6.3. Воздух насыщен паром этилового спирта. Общее давление воздушно-паровой
смеси 600 мм рт. ст., температура 60°С. Принимая оба компонента смеси за идеальные
газы, определить относительную массовую концентрацию Y этилового спирта в
смеси и плотность смеси.
6.4. Газ состава : водород 26%, метан 60%, этилен 14% (проценты мольные) имеет
давление рабс=30 кгс/см2 и температуру 20°С. Считая компоненты смеси идеальными
газами, определить их объемные массовые концентрации С y (в кг/м3).
6.5.Показать, что в формуле
СyMВ
y
ρ  C y M В  M А 
при любых значениях Мв и МА у не может быть отрицательным.
6.6. В условиях примера 6.3 (а) определить движущую силу процесса массоперехода в начальный момент времени по газовой и по жидкой фазе в объемных
концентрациях, мольных и массовых.
6.7. Пар бинарной смеси хлороформ – бензол, содержащий 50% хлороформа и 50%
бензола, вступает в контакт с жидкостью, содержащей 44% хлороформа и 56%
бензола (проценты мольные). Давление атмосферное. Определить: а) из какой фазы в
какую будут переходить хлороформ и бензол; б) движущую силу процесса
массопередачи по паровой и по жидкой фазе на входе пара в жидкость (в мол.
долях).
6.8. Смесь воздуха с паром четыреххлористого углерода, сжатая до абсолютного
давления 10 кгс/см2, охлаждается в трубчатом водяном холодильнике. При 40°С
начинается конденсация четыреххлористого углерода. Определить: а) массовый
процент его в воздухе в начальной смеси и б) степень выделения из газовой смеси
после охлаждения ее до 27°С.
6.9. Газовая смесь, содержащая 0,8% (об.) октана, сжимается компрессором до
рабс–5 кгс/см3 и затем охлаждается до 25°С. Определить степень выделения октана.
Как изменится степень выделения, если охладить сжатую газовую смесь
холодильным рассолом до 0°С?
6.10. Рассчитать коэффициенты молекулярной диффузии под атмосферным
давлением: а) пара бензола в паре толуола при температуре 100°С; б) пара этилового
спирта в водяном паре при температуре 92°С.
6.11. Определить коэффициент массопередачи в орошаемом водой абсорбере, в
котором βy, = 2,76·10-3 кмоль/(м2·ч·кПа), а βх = 1,17·10-4 м/с. Давление в аппарате рабс
= = 1,07 кгс/см2. Уравнение линии равновесия в мольных долях: у* = 1,02х.
6.12.Определить среднюю движущую силу и общее число единиц переноса п0у
при поглощении из газа паров бензола маслом. Начальная концентрация. бензола в
газе 4% (об.); улавливается 80% бензола. Концентрация бензола в масле, вытекающем
из скруббера, 0,02 кмоль бензола/кмоль чистого масла. Масло, поступающее в
скруббер, бензола не содержит. Уравнение равновесной линии в относительных
мольных концентрациях:
Y   0.126X
Движущую силу выразить в единицах концентрации Y (кмоль бензола/кмоль
инертного газа),
307
6.13.В скруббере поглощается водой двуокись серы из инертного газа (азота) под
атмосферным давлением (760 мм рт. ст.). Начальное содержание двуокиси серы в
газе 5% (об.). Температура воды 20°С, ее расход на 20% больше теоретически
минимального. Извлекается из газа 90% SO2 . Определить: 1) расход воды на
поглощение 1000 кг/ч сернистого газа; 2) среднюю движущую силу процесса;
3)общее число единиц переноса N0Y . Линия равновесия может быть принята за
прямую; координаты двух ее точек: 1) парциальное давление SO2 в газовой фазе
ρ = 39мм рт. ст., X = 0,007 кг SO2 /кг воды; 2) ρ =26 мм рт. ст., X = 0,005 кг
SO 2 /кг воды.
6.14. В насадочном абсорбере производится поглощение пара метилового спирта
водой из газа под атмосферным давлением при средней температуре 27°С.
Содержание метилового спирта в газе, поступающем в скруббер, 100 г на 1м 3
инертного газа (считая объем газа при рабочих условиях). На выходе из
скруббера вода имеет концентрацию 67% от максимально возможной, т.е. от
равновесной с входящим газом. Уравнение растворимости метилового спирта в воде
в относительных мольных концентрациях: Y* = 1,15X. Извлекается водой 98% от
исходного количества спирта. Коэффициент массопередачи:
кмоль спирта 

К х  0,5к,5км спирта/ м 2  ч

кмоль воды 

Расход инертного газа 1200 м 3 /ч (при рабочих условиях). Абсорбер заполнен
насадкой из керамических колец с удельной поверхностью 190 м2/м3. Коэффициент
смачивания насадки ψ = 0,87. Фиктивная скорость газа в абсорбере ω= 0,4 м/с.
Определить расход воды и требуемую высоту слоя насадки.
6.15. В скруббер диаметром 0,5 м подается 550 м 3 /ч (при 760 мм рт. ст. и20°С)
воздуха, содержащего 2,8% (об.) аммиака, который поглощается водой под
атмосферным давлением. Степень извлечения аммиака 0,95. Расход воды на 40%
больше теоретически минимального. Определить 1) расход воды; 2) общее число
единиц переноса N0Y 3) высоту слоя насадки из керамических колец 50×50×5 мм.

кмоль аммиака 

Коэффициент массопередачи: К y  0,001 кмоль аммиака/  м 2  с
кмоль воздуха 

Данные о равновесных концентрациях жидкости и газа взять из примера 6.10.
Коэффициент смоченности насадки ψ= 0,9.
6.16. Вывести формулу для определения высоты единицы переноса в насадочном
абсорбере для жидкой фазы h х из критериального уравнения (6.46).
6.17. Воздух с примесью аммиака пропускается через орошаемый водой скруббер,
заполненный насадкой из колец с удельной поверхностью 89,5 м2 /м3 . Свободный
объем насадки 0,79 м 3/м3. Температура абсорбции 28°С, абсолютное давление 1
кгс/см3. Среднее содержание аммиака в газовой смеси 5,8% (об.). Массовая скорость
газа, отнесенная к полному сечению скруббера, 1,1кг/(м 2 ·с). Определить
коэффициент массоотдачи для газа, считая, что скруббер работает при пленочном
режиме.
6.18. Рассчитать коэффициент массоотдачи от жидкой фазы в насадочном
абсорбере, в котором производится поглощение двуокиси углерода водой при
температуре 20°С. Плотность орошения 60 м3/(м2·ч). Насадка – керамические кольца
35×35×4 мм навалом. Коэффициент смоченности насадки ψ = 0,86.
6.19. Определить коэффициент массоотдачи для газа в скруббере при
поглощении пара бензола из коксового газа по следующим данным: насадка
хордовая из реек 12,5×100 мм с расстоянием между рейками b = 25 мм (для такой
насадки d э = 2b = 0,05 м); скорость газа, считая на полное сечение скруббера,
0,95 м/с; плотность газа 0,5 кг/м3; динамический коэффициент вязкости газа 0,013
мПа·с; коэффициент диффузии бензола в газе 16·10 -6 м2 /с. Режим считать
пленочным.
6.20. Определить диаметр и высоту тарельчатого абсорбера для поглощения
водой аммиака из воздушно-аммиачной смеси при атмосферном давлении и
температуре 20°С. Начальное содержание аммиака в газовой смеси 7% (об .).
Степень извлечения 90%. Расход инертного газа (воздуха) 10 000 м 3 /ч (при
рабочих условиях). Линию равновесия считать прямой, ее уравнение в
относительных массовых концентрациях: Y  =0.61 X Скорость газа в абсорбере
(фиктивная) 0,8 м/с. Расстояние между тарелками 0,6 м. Средний к.п.д. тарелок
0,62. Коэффициент избытка поглотителя φ = 1,3.
308
6.21. По условиям предыдущей задачи определить. 1) высоту насадочного
абсорбера с насадкой из керамических колец 50×50×5 мм, приняв h э – высоту слоя
насадки, эквивалентную теоретической тарелке (ВЭТТ), равной 0,85 м; 2) величину
коэффициента
массопередачи
в
этом
насадочном

кг аммиака 
 ,считая
абсорбере К y кг аммиака/  м 2  с
коэффициент
смоченности
кг воздуха 

насадки ψ равным 0,9.
6.22. По данным контрольных задач 6.20 и 6.21 определить высоту слоя насадки
через общее число единиц переноса n0у и высоту единицы переноса (ВЕП) h0y.
6.23. Абсорбер для улавливания паров бензола из парогазовой смеси орошается
поглотительным маслом с мольной массой 260 кг/кмоль. Среднее давление в
абсорбере р абс = 800 мм рт, ст., температуре 40 °С. Расход парогазовой смеси
3600 м 3 /ч (при рабочих условиях). Концентрация бензола в газовой смеси на
входе в абсорбер 2% (об.); извлекается 95% бензола. Содержание бензола в
поглотительном масле, поступающем в абсорбере после регенерации, 0,2% (мол.).
Расход поглотительного масла в 1,5 раз больше теоретически минимального. Для
расчета равновесных составов принять, что растворимость бензола в масле
определяется законом Рауля. При концентрациях бензола в жидкости до X = 0,1
кмоль бензола/кмоль масла равновесную зависимость Y* = f(Х) считать
прямолинейной
Определить:·1) расход поглотительного масла в кг/ч; 2) концентрацию
бензола в поглотительном масле, выходящем из абсорбера; 3) диаметр и высоту
насадочного абсорбера при скорости газа в нем (фиктивной) 0,5 м/с и высоте
единицы переноса (ВЕП) h 0y = 0,9 м; 4) высоту тарельчатого абсорбера при
среднем к.п.д. тарелок 0,67 и расстоянии между тарелками 0,4 м
6.24. В насадочном абсорбере диаметром 1 м двуокись серы поглощается водой
из воздуха. Начальное содержание SO2 в поступающей смеси 7% (об.). Степень
поглощения 0,9. На выходе из абсорбера вода содержит 0.0072 кг SΟ2 /кг воды.

кг SO 2 

Коэффициент массопередачи в абсорбере K y  0.005кг SO 2 /  м 2  с
кг воздуха 

Насадка из керамических колец 50×50×5 мм Коэффициент смоченности
насадки ψ = 1. Высота единицы переноса h0y =1,17 м. Определить расход воды в
абсорбере.
6.25. В абсорбере под атмосферным давлением при температуре 20°С
поглощается из парогазовой смеси 300кг бензола в 1 ч. Начальное содержание
пара бензола в парогазовой смеси 4%(об.). Степень извлечения бензола 085.
Жидкий поглотитель, поступающий в абсорбер после регенерации, содержит 0,0015
кмоль бензола /кмоль поглотителя. Фиктивная скорость газа в абсорбере 0,9 м/с.
Уравнение линии равновесия: Y* = 0,2 Х, где Y* и X выражены соответственно в
кмоль бензола /кмоль инертного газа и кмоль бензола /кмоль поглотителя.
Коэффициент избытка поглотителя φ = 1,4. Определить диаметр абсорбера и
концентрацию бензола в поглотителе, выходящем из абсорбера.