Свойства и график функции у=arcsinx, y=arccosx
реклама
Свойства и график функции у=arcsinx
1. Область определения функции у=arcsinx – промежуток [ - 1; 1].
𝜋
𝜋
2
2
2. Область (множество) значений функции – промежуток [− ; ].
3. Функция у=arcsinx не является периодической.
𝜋
4. Наименьшее значение у=− функция принимает в точке – 1.
2
𝜋
Наибольшее значение у= функция принимает в точке 1.
2
5. Нулем функции является значение аргумента х=0.
6. Функция принимает отрицательные значения на промежутке [ - 1; 0) и
положительные значения на промежутке (0; 1].
7. Функция у=arcsinx нечетная.
8. Функция у=arcsinx возрастающая в области определения.
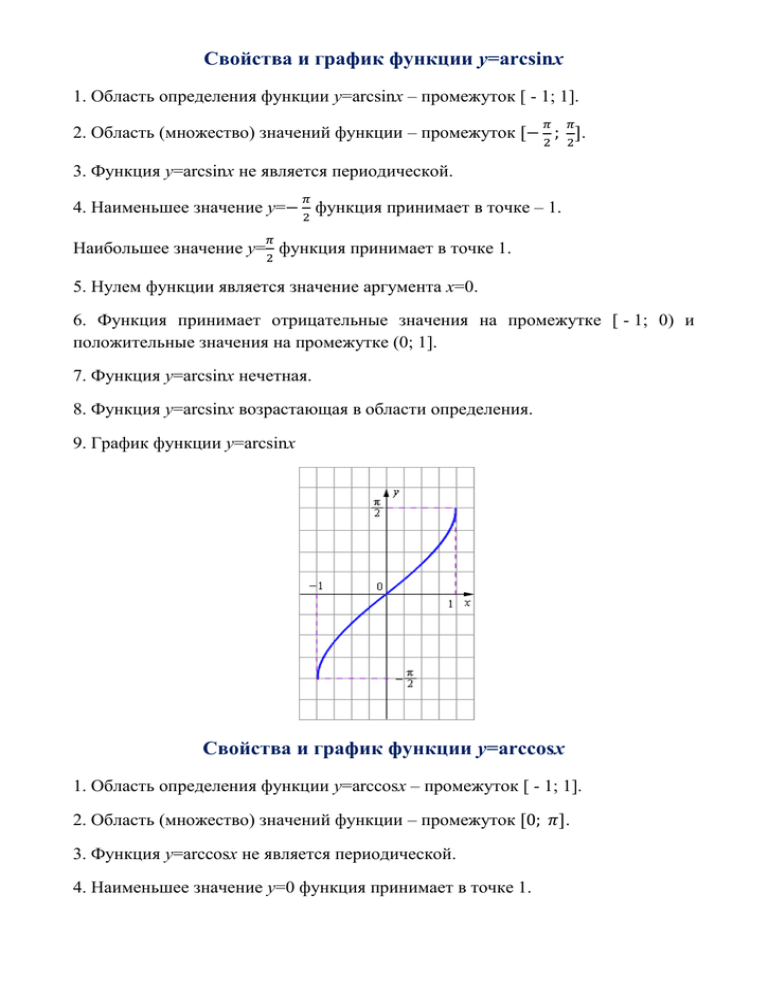
9. График функции у=arcsinx
Свойства и график функции у=arccosx
1. Область определения функции у=arccosx – промежуток [ - 1; 1].
2. Область (множество) значений функции – промежуток [0; 𝜋].
3. Функция у=arccosx не является периодической.
4. Наименьшее значение у=0 функция принимает в точке 1.
Наибольшее значение у= функция принимает в точке - 1.
5. Нулем функции является значение аргумента х=1.
6. Функция принимает отрицательных значений не принимает, положительные
значения принимает на промежутке [ - 1; 1].
7. Функция у=arccosx не является нечетной и не является четной.
8. Функция у=arccosx убывающая в области определения.
9. График функции у=arccosx
Примеры решения задач
Пример 1. Решите уравнение arcsin(3x+5)=0,
Решение. 3х+5=0, х=−
5
3
Ответ: −
5
3
𝑥
Пример 2. Решите уравнение arccos ( − 4) = 𝜋.
3
Решение. Функция arccos принимает значение
в точке – 1,
𝑥
следовательно, − 4= - 1, отсюда х=9.
3
Ответ: 9
𝜋
Пример 3. Решите неравенство arcsin(2𝑥 + 1) < .
3
𝜋
π
3
2
𝜋
Решение. По условию arcsin(2𝑥 + 1) < , т.е. − ≤ arcsin(2𝑥 + 1) < .
π
3
𝜋
Это равносильно неравенству sin(− ) ≤ sin(arcsin(2𝑥 + 1)) < sin( ), −1 ≤
2
2𝑥 + 1 <
√3
,
2
−1 ≤ 𝑥 <
3
√3−2
4
Ответ: [ - 1;
√3−2
)
4
𝜋
Пример 4. Докажите тождество arcsin 𝑥 + + arccos 𝑥 = .
2
𝜋
Решение.
arccos 𝑥 ↔ {
𝜋
2
Пусть
𝜋
− ≤𝑦≤ ,
2
𝑦 = arcsin 𝑥 ↔ { 2
sin 𝑦 = 𝑥
пусть
также
𝑧=
0 ≤ 𝑧 ≤ 𝜋,
. Следовательно, требуется доказать неравенство 𝑦 + 𝑧 =
cos 𝑧 = 𝑥
.
Перенесём z в правую часть и возьмём синус от обеих частей
𝜋
𝜋
получившегося равенства: 𝑦 = − 𝑧 → sin 𝑦 = sin( − 𝑧) = cos 𝑧. Но sin y = x и
2
2
cos z = x, значит, наше равенство принимает вид x = x. Однако для того, чтобы
доказать нужное нам тождество, мы должны обосновать возможность перехода
от верного равенства x = x к исходному.
𝜋
В самом деле, переход от равенства sin y = cos z к равенству 𝑦 = − 𝑧
2
вообще говоря, не является равносильным преобразованием. Но у нас есть
𝜋
𝜋
ограничения на y и z в виде неравенств − ≤ 𝑦 ≤ , 0 ≤ 𝑧 ≤ 𝜋, а для таких y и z
2
𝜋
2
равенство sin y = cos z возможно только при 𝑦 = − 𝑧.
2
Следовательно, 𝑦 + 𝑧 =
𝜋
𝜋
и наконец, arcsin 𝑥 + + arccos 𝑥 = что и
2
2
требовалось доказать.
Пример 5. Найти sin(arccos0,75).
𝜋
Решение. Так как 0arccos0,75 , то 0sin(arccos0,75)1. Поэтому
2
sin(arccos0,75)=√1 − cos 2 (arccos 0,75)=√1 − 0,752 =0,25√7.
Ответ: 0,25√7
Пример 6. Решите уравнение 3arcsin√𝑥 - =0.
3arcsin√𝑥 - =0
Решение.
𝜋
√3
3
sin(arcsin√𝑥)=sin √𝑥= x= .
3
2
4
3arcsin√𝑥=
𝜋
arcsin√𝑥=
3
Ответ:
3
4
Упражнения
1. Укажите область определения и область значения функции:
𝑥
1) 𝑓(𝑥) = arcsin 3𝑥
2) 𝑓(𝑥) = arcsin(− )
4) 𝑓(𝑥) = arccos 2𝑥
5) 𝑓(𝑥) = arccos(− )
7) 𝑓(𝑥) = arccos(−5𝑥)
8) 𝑓(𝑥) = arccos(−
𝑥
3) 𝑓(𝑥) = arcsin(− − 3)
2
2
𝑥
6) 𝑓(𝑥) = arcsin
6
2𝑥
3
+ 1)
9) 𝑓(𝑥) = arccos
2
𝑥
6
𝑥
10) 𝑓(𝑥) = arcsin(−3𝑥)
2. Укажите координаты точек пересечения с осями Ох и Оу графика функции:
1) 𝑦 = arcsin(2 − 0,1𝑥)
2) 𝑦 = arcsin(𝑥 2 + 2𝑥 + 1)
3) 𝑦 = arccos(4𝑥 2 − 4𝑥 + 1)
4) 𝑦 = arccos(0,6 − 12𝑥)
5) 𝑦 = arcsin(𝑥 2 − 2𝑥 + 1)
6) 𝑦 = arccos(4𝑥 2 + 4𝑥 + 1)
7) 𝑦 = arccos(4 − 0,2𝑥)
8) 𝑦 = arcsin(3 − 𝑥)
9) 𝑦 = arccos(6 − 2𝑥)
10) 𝑦 = arcsin(0,5 − 5𝑥)
3. Определите, четной или нечетной является функция:
1) 𝑓(𝑥) = sin 𝑥 +
3) 𝑓(𝑥) = tg 𝑥 −
arccos |𝑥|
2) 𝑓(𝑥) = arcsin 𝑥 + 4 arcsin 2𝑥
2 arcsin 𝑥
5 arccos |𝑥|
4) 𝑓(𝑥) = arcsin 𝑥 arcsin 2𝑥
arcsin 𝑥
5) 𝑓(𝑥) = arcsin2 𝑥 + sin 𝑥 arcsin 2𝑥
6) 𝑓(𝑥) = √arcsin2 𝑥 + 4 arccos |𝑥|
7)
8)
9)
10)
4. Функция задана на множестве D. Укажите для нее:
а) наименьшее и наибольшее значение;
б) промежутки возрастания и убывания;
в) промежутки, где функция принимает отрицательные и положительные
значения;
г) нули функции
1
1) 𝑓(𝑥) = arcsin 𝑥, 𝐷 ∈ [0; ]
2
1 1
3) 𝑓(𝑥) = arccos 𝑥, 𝐷 ∈ [− ; ]
2 2
5) 𝑓(𝑥) = arcsin 𝑥, 𝐷 ∈ [−
√3 1
; ]
2 2
1
2) 𝑓(𝑥) = arccos 𝑥, 𝐷 ∈ [− ; 0)
2
4) 𝑓(𝑥) = arcsin 𝑥, 𝐷 ∈ [−
√2 √2
; ]
2
2
6) 𝑓(𝑥) = arcsin 𝑥, 𝐷 ∈ [−
√3 √2
; ]
2
2
7)
8)
9)
10)
5. Решите уравнения:
1) arcsin(1 − 2𝑥) = −
𝜋
2) arccos(𝑥 2 + 14𝑥 + 12) = 0
2
3) arccos(3 − 6𝑥) = 𝜋
4) arccos(12𝑥 + 1) = −
𝜋
5) arccos(15 − 2𝑥 − 𝑥 2 ) =
2
7) arcsin(𝑥 2 + 10𝑥 − 23) =
𝜋
2
9) arcsin(𝑥 2 − 10𝑥 + 9) = 0
𝜋
2
6) arcsin(10𝑥 − 6) = 𝜋
8)
10)
6. Решите неравенство:
1) arcsin(𝑥 + 1) ≤ 0
4) arccos 𝑥 ≤
2) arcsin(5 − 4𝑥) ≥ −
𝜋
2
5) arccos(𝑥 − 12) ≥ 𝜋
4
7) arcsin(4𝑥 − 2) ≥ −
10) arcsin 𝑥 <
𝜋
𝜋
2
8) arccos 𝑥 ≥
2𝜋
3) arccos(𝑥 + 10) ≤ 0
6) arcsin 𝑥 ≥ −
𝜋
3
9) arccos(6𝑥 − 1) ≥
3
𝜋
6
7. При каких значениях р верно равенство:
1) arcsin2 𝑥 = 𝑝
4) arcsin 𝑥 = 𝑝 +
7)
2) | arccos 𝑥| = 𝑝
𝜋
2
5) arcsin 𝑥 =
8)
10)
8. Постройте график функции:
𝑝
𝑝+0,4𝜋
3) arccos 𝑥 = −𝑝 − 𝜋
6) arccos 𝑥 =
9)
𝑝−0,1𝜋
𝑝
𝜋
2
1) 𝑦 = − arcsin 𝑥
2) 𝑦 = − arccos 𝑥
5) 𝑦 = 2 arcsin 𝑥
6) 𝑦 = arccos 𝑥
9) 𝑦 = | arcsin 𝑥|
10) 𝑦 = arccos |𝑥|
1
2
3) 𝑦 = arccos(−𝑥)
7) 𝑦 = arccos
𝑥
3
4) 𝑦 = arcsin(−𝑥)
8) 𝑦 = arcsin
9. Постройте график функции:
𝑥
1
1) 𝑦 = 2 arcsin ( + ) − 1,5
2
2
𝑥
2) 𝑦 = |0,5 arcsin 𝑥 − 1|
3) 𝑦 = −2 arccos ( + 1) + 3
4) 𝑦 = |0,5 arccos 𝑥 − 1|
5) 𝑦 = 3 arccos(2𝑥 − 6) + 3
6) 𝑦 = | arccos(2𝑥 + 6) − 2|
7) 𝑦 = −4 arcsin(3𝑥 − 1) + 1
8) 𝑦 = | arcsin(2𝑥 + 4) − 1|
9) 𝑦 = 1 − arcsin(2𝑥 − 1)
10) 𝑦 = −2 arccos(2𝑥 − 3)
2
3
2
3
2
𝑥
2

