Урок математики в 8 классе по теме

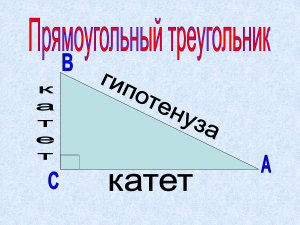
1
Урок математики в 8 классе по теме: «Синус, косинус и тангенс острого угла
прямоугольного треугольника»
Цели урока:
Образовательные:
формировать понятия синуса, косинуса и тангенса острого угла прямоугольного треугольника;
Развивающие:
развивать способности к самостоятельному планированию и организации работы; навыки
коррекции собственной деятельности через применение информационных технологий; умение
обобщать, абстрагировать и конкретизировать знания
Воспитательные:
воспитывать познавательный интерес к математике, информационную культуру и культуру
общения, самостоятельность, способность к коллективной работе.
Оборудование: интерактивная доска, компьютерная презентация по теме.
Тип урока: урок изучения и первичного закрепления новых компетенций
Методы: проблемно-поисковый, индуктивный, метод групповой работы, самостоятельной
работы.
Ход урока:
Организационный момент.
Мобилизация учебной деятельности учащихся: доброжелательный настрой учителя и учащихся,
быстрое включение класса в деловой ритм, организация внимания всех учащихся, полная
готовность класса и оборудования к работе.
I этап. Обеспечение мотивации и принятия учащимися цели учебно-познавательной
деятельности, актуализация опорных знаний и умений.
1) Сообщение целей и задач урока.
2) Проверка домашнего задания: выявление факта выполнения домашнего задания у всех
учащихся, обнаружение причин невыполнения домашнего задания отдельными учащимися,
устранение типичных ошибок
II этап. Актуализация ЗУН, необходимых для творческого применения знаний.
Математический диктант по готовому чертежу на доске.
1. Назовите стороны треугольника МРК.
2. Чему равна сумма углов треугольника?
3. Сформулировать теорему о соотношениях между сторонами и углами треугольника.
4.Сформулировать следствие о величине гипотенузы и катета в прямоугольном треугольнике.
5.Сформулировать свойство катета прямоугольного треугольника, лежащего против угла 30°.
III этап. Усвоение новых компетенций и способов действий
1.Ввести понятие катетов, прилежащих к противолежащему углу.
2.Ввести понятие синуса, косинуса, тангенса острого угла прямоугольного треугольника, их
обозначения.
Пусть АВС – прямоугольный треугольник с прямым углом С и острым углом при вершине А,
равным  .
2
В
С
А
АВ – гипотенуза
ВС - катет
АС - катет
Синусом острого угла в прямоугольном треугольнике называется отношение противолежащего
катета к гипотенузе.
BC
sin A 
AB
Косинусом острого угла в прямоугольном треугольнике называется отношение прилежащего
катета к гипотенузе.
AC
cos A 
AB
Тангенсом острого угла в прямоугольном треугольнике называется отношение противолежащего
катета к прилежащему.
BC
tgA 
AC
Эти правила позволяют, зная одну из сторон прямоугольного треугольника и острый угол,
находить две другие стороны; зная две стороны, находить острые углы.
a = c sin α
b = c cos α
a = b tg α
b = a ctg α
IV этап. Первичная проверка понимания
Творческая работа
Решить задачу. В прямоугольном треугольнике даны гипотенуза с и острый угол α. Найти
катеты, их проекции на гипотенузу и высоту, опущенную на гипотенузу.
С

А
D
c
Решение.
AC = AB cos α = c cos α;
BC = AB sin α = c sin α;
BD = BC sin α = c sin² α;
В
3
V. Закрепление знаний и способов действий.
Решение прикладных задач
1.Найти высоту дерева, если расстояние от наблюдателя до ствола дерева равно 9м, а угол, под
которым он видит макушку дерева, равен 300.
3.Тень от вертикально стоящего шеста, высота которого 3 3 м, составляет 3 м.
Выразите в градусах высоту Солнца над горизонтом.
помощи шарниров. Определите силу, действующую на стержни, если САВ = 90, а АСВ= 60.
Кроссворд
VI. Домашнее задание: учить п.66 №59, № 594, №595
4
Информационные материалы.
1. Пифагор. Занимательная математика. Халамайзер А.Я. Москва
2. «Высшая школа» 1994г.
3. Живая математика. Перельман Я. И. Москва «Наука» 1978 г.
4. Интеллектуальный пир. Серия «Клуб эрудитов» Выпуск 2. Кострома ИМЦ «Вариант»
1993 г.
5. Коллекция 80000 анимаций. - www.animashky.ru
6. Большая энциклопедия Кирилла и Мефодия, 8 CD-ROM, 2002 г.
7. Электронные ресурсы сайта «Сеть творческих учителей»
8. 8.Электронные ресурсы сайта «Фестиваль педагогических идей «Открытый урок»
9. Учебное электронное пособие «Математика 5-11», Дрофа
10. Учебно-методическое пособие. Взаимосвязь теории с практикой в процессе изучения
математики. Возняк Г.М., Маланюк М.П. Киев. «Радянська школа»